Hamiltonian Cycle

What is Hamiltonian Cycle?

Hamiltonian Cycle or Circuit is a path in an undirected graph that visits all the vertices in the graph exactly once and terminates back at the starting node.

Problem Statement

Given an undirected graph, our task is to determine whether the graph contains a Hamiltonian cycle or not.

Example

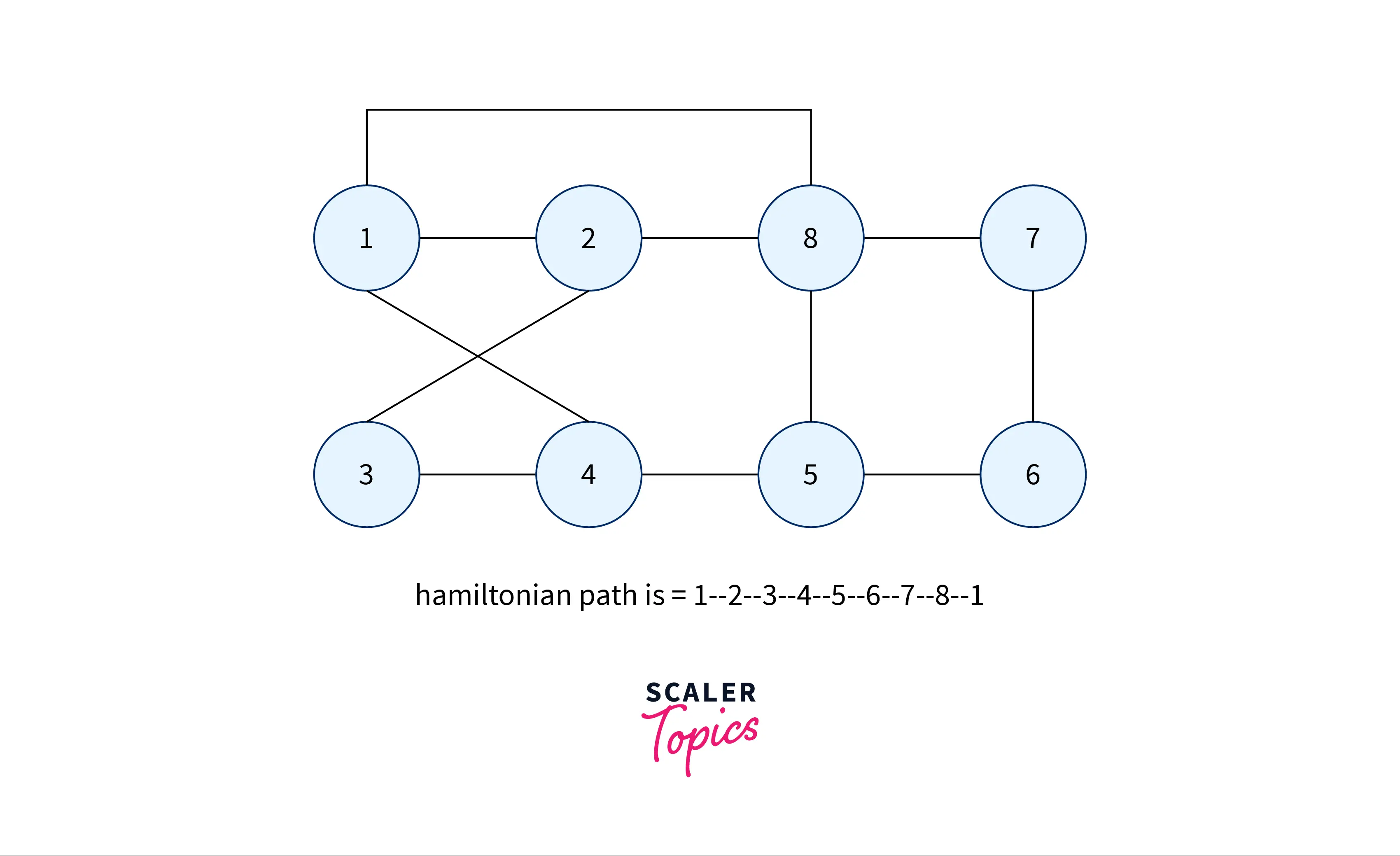
Explanation

In the above example, we are given an undirected having 8 vertices. We start traversing from vertex 1 and are able to visit every vertex exactly once and return back to vertex 1 which is the starting vertex.

Input/ Output

Input is the adjacency matrix of a graph G(V, E), where V is the number of Vertices and E is the number of Edges. An adjacency matrix represents the adjacency of two vertices in constant time.

In Output, we have to Return True (boolean value) along with the path if the graph contains a Hamiltonian cycle, otherwise returns False.

Constraints

• The graph is undirected.
• The task is to determine the presence of a Hamiltonian cycle in the graph.
• A Hamiltonian cycle is a cycle that visits every vertex exactly once and returns to the starting vertex.

Approach - Naive Algorithm

In this approach, we will use Dynamic Programming and Bit Masking techniques to check whether there exists a Hamiltonian Cycle or not.

• Algorithm

  1. Initialize a boolean matrix dp[][] having dimension $N*2^{N}$, where dp[j][i] represents whether there exists a path for the given subset or not.
  2. For the base case, update dp[i][1 << i] = true, for i in range [0, N – 1].
  3. Iterate over the range [1, $2^{N}$ – 1] using and perform the following steps:
     • All the vertices with bits set in mask i, are included in the subset.
     • Iterate over the range [1, N] using the variable j that will represent the end vertex of the hamiltonian path of current subset mask i and perform the following steps:
       • If the value of i and $2^{j}$ is true, then iterate over the range [1, N] using the variable k and if the value of dp$[k][i^{2^{j}}]$ is true, then mark dp[j][i] is true and break out of the loop.
       • Otherwise, continue to the next iteration.
  4. Iterate over the range using the variable i and if the value of dp[i][$2^{N}$ – 1] is true, then there exists a hamiltonian path ending at vertex i.

• Implementation

  Let us now see the implementation of the Hamiltonian Cycle using the naive approach in the following Graph in C++:

Output:

Let us now see the implementation of the Hamiltonian Cycle using the naive approach of the above-shown graph in Java:

Output:

Let us now see the implementation of the Hamiltonian Cycle using the naive approach of the above-shown graph in Python:

Output:

• Time Complexity

  Time Complexity for finding the Hamiltonian Cycle using the naive approach is $O(N*2^{N})$, where N is the number of vertices in the graph.

• Space Complexity

  Since we are using the boolean matrixdp[][] as an auxiliary space, the space complexity for finding the Hamiltonian Cycle using the naive approach is $O(N*2^{N})$.

Approach - Backtracking

The optimal Approach for this problem will be to solve it using the concept of backtracking. The following algorithm demonstrates the working of the backtracking approach:

• Algorithm

  1. Create an empty path array and add vertex 0 to it.
  2. Start adding other vertices by checking if they have been added previously or not.
  3. We can check this by creating a visiting array to check if the vertex has already been visited or is adjacent to the previously added vertex.
  4. If any such vertex is found, add it to the path array and backtrack from there.
  5. If no such vertex is found we return False.

• Implementation

Let us now see the implementation of the Hamiltonian Cycle of the following two Graphs in C++:

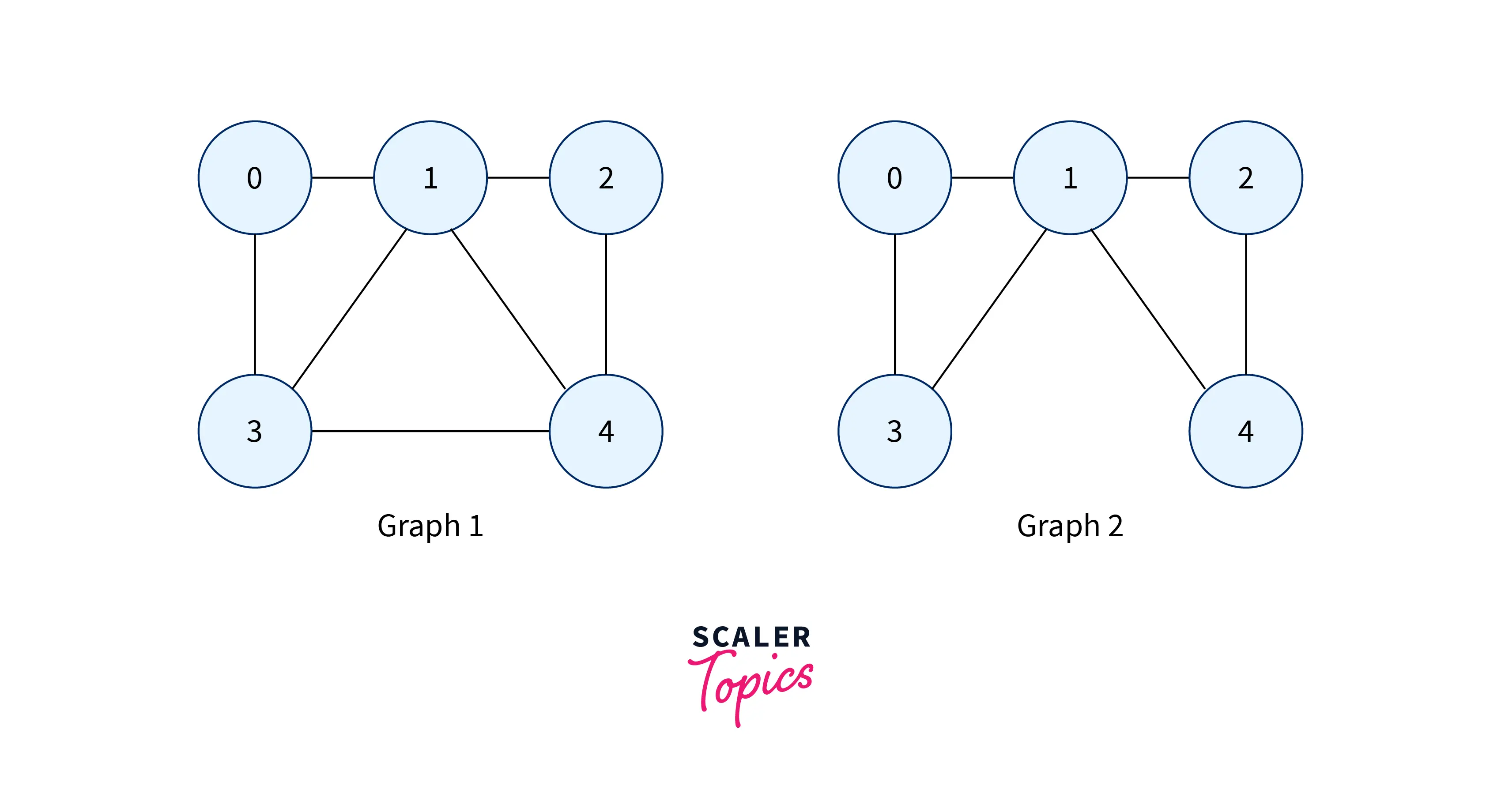
Output:

Let us now see the implementation of the Hamiltonian Cycle in the above shown Graphs in Java:

Output:

Let us now see the implementation of the Hamiltonian Cycle above shown in two Graphs in Python:

Output:

In the above implementation, the hamiltonianCycle function solves the Hamiltonian Cycle problem using Backtracking. It mainly utilizes hamiltonianUtil() function to solve the problem. It returns False if there is no Hamiltonian Cycle possible, otherwise, returns true and prints the cycle.

• Time Complexity

  Time Complexity for finding the Hamiltonian Cycle using the Backtracking approach is O(N!), where N is the number of vertices in the graph.

• Space Complexity

  Since we are not using any auxiliary space, the space complexity for finding the Hamiltonian Cycle using the Backtracking approach is O(1).