Hill Climbing Algorithm in AI

Hill Climbing Algorithm in Artificial Intelligence

Hill climbing in AI is employed to solve various optimization problems. It begins with an initial solution and iteratively explores neighboring solutions by making incremental changes. If a neighboring solution provides a better value of the objective function, it is accepted as the current solution. This process continues until no further improvements can be made, or a stopping criterion is met.

Advantages of Hill Climbing Algorithm

1. Simplicity: Hill climbing is straightforward to understand and implement, making it an excellent choice for solving basic optimization problems.
2. Memory Efficiency: It doesn't require significant memory resources since it only stores the current state and explores nearby solutions.
3. Quick Convergence: Hill climbing often converges rapidly to a local maximum, making it suitable for problems where finding a good solution quickly is more critical than finding the global optimum.

Disadvantages of Hill Climbing Algorithm

1. Local Optima: Hill climbing is prone to getting stuck in local optima, especially in complex, multi-modal landscapes where multiple peaks exist.
2. Lack of Exploration: It can be myopic, as it only explores nearby solutions. It may miss a globally optimal solution if it requires moving away from the current position initially.
3. Sensitivity to Initial State: The quality of the solution found is highly dependent on the initial state, making it sensitive to the starting point.

Features of Hill Climbing

Hill climbing possesses several distinctive features:

1. Deterministic: Imagine you are planning a route for a delivery truck. If you use Hill Climbing with the same starting point and the same map, it will always suggest the same route.

• Deterministic Nature: Hill Climbing is a deterministic optimization algorithm, which means that given the same initial conditions and the same problem, it will always produce the same result. There is no randomness or uncertainty in its operation.
• Reproducibility: This determinism makes Hill Climbing predictable and reproducible. Researchers and practitioners can rely on consistent results, making it easy to understand and debug.

2. Greedy: Think of a salesperson trying to visit multiple cities to sell products. Hill Climbing might suggest going to the nearest city first at each step. While this seems efficient in the short term, it may not result in the overall shortest route, potentially leading to longer travel times.

• Greedy Selection: Hill Climbing is inherently greedy in its approach. At each step, it makes a choice that appears to be the best in the immediate context without considering the long-term consequences.
• Immediate Improvement: It always selects the neighboring solution that provides the best improvement in the objective function. This myopic decision-making process can lead to suboptimal solutions, especially if the algorithm gets trapped in local optima.

3. Local Search: Consider an assembly line in a manufacturing plant. Hill Climbing could be applied to optimize the speed of each machine. It would make small adjustments to the machine speeds within their current capabilities, ensuring efficient production without risking major disruptions.

• Local Neighborhood: Hill Climbing operates within a local neighborhood of the current solution. It explores solutions that are closely related to the current state by making small, incremental changes.
• Efficiency: This local search strategy can be efficient when finding a solution that is reasonably close to the initial state is sufficient. It often converges quickly to a local maximum or minimum.
• Limitation: However, the local search nature of Hill Climbing is also its limitation. It may miss better solutions that exist outside the immediate neighborhood, such as global optima, because it doesn't explore the entire solution space.

In summary, Hill Climbing is a deterministic, greedy, and local search algorithm. Its deterministic nature ensures consistent results, its greedy approach focuses on immediate improvements, and its local search strategy explores nearby solutions. While these features make Hill Climbing relatively simple and efficient, they also limit its ability to handle more complex optimization landscapes and find global optima. Researchers often use variations and enhancements of Hill Climbing to overcome these limitations in practical applications.

Types of Hill Climbing

Hill climbing comes in several flavors, each with its own approach to finding the optimal solution:

1. Simple Hill Climbing

Simple Hill Climbing is the most basic form of the algorithm. It iteratively makes small moves to neighboring solutions, accepting a new solution only if it improves the objective function. If it doesn't, the algorithm terminates. This method is limited by its tendency to get stuck in local optima.

While Simple Hill Climbing has advantages such as simplicity and memory efficiency, it also has limitations. It can get stuck in local optima, miss global optima, and its performance is sensitive to the initial solution. To address these limitations, more advanced variants and enhancements of hill climbing algorithms have been developed, such as steepest-ascent hill climbing, simulated annealing, and genetic algorithms, which offer improved exploration of the solution space and better convergence properties.

2. Steepest-Ascent Hill Climbing

Steepest-Ascent Hill Climbing, also known as steepest ascent or gradient ascent, takes a more rigorous approach. It explores all neighboring solutions and selects the one that offers the most significant improvement in the objective function. This helps mitigate the problem of getting stuck in local optima to some extent.

Steepest-Ascent Hill Climbing is called "steepest" because it rigorously explores all possible moves before deciding on the best one. This approach helps mitigate the problem of getting stuck in local optima, as it can escape from a local peak by considering all available options.

However, Steepest-Ascent Hill Climbing does come with a trade-off – it can be computationally more demanding than the basic hill climbing algorithm since it needs to evaluate the objective function for all neighboring solutions. Despite this, it's a valuable variant when the goal is to improve the ability to find better solutions in optimization problems.

3. Stochastic Hill Climbing

Stochastic Hill Climbing introduces an element of randomness. Instead of always selecting the best neighboring solution, it probabilistically accepts solutions that are worse than the current one. This randomness allows the algorithm to explore a broader solution space, potentially escaping local optima.

Stochastic Hill Climbing's stochastic nature allows it to explore a wider range of solutions, potentially escaping local optima that deterministic hill climbing algorithms might get trapped in. It is particularly useful in situations where a more exploratory approach is desired, and it's not necessary to find the absolute best solution but rather a satisfactory one.

However, the randomness in Stochastic Hill Climbing can also be a drawback because it may lead the algorithm to accept inferior solutions more frequently, making it less efficient in converging to optimal or near-optimal solutions. To mitigate this, variants of Stochastic Hill Climbing often include strategies for controlling the degree of randomness, such as simulated annealing.

State-space Diagram for Hill Climbing

In the context of the Hill Climbing algorithm, the state space diagram is a visual representation of the landscape of possible solutions for an optimization problem. It helps us understand the different regions within this landscape.

To visualize how the hill climbing algorithm works, we can represent it using a state-space diagram. In this diagram:

• Each point represents a state or a potential solution.
• Arrows between points represent transitions between states.
• The height of each point indicates the value of the objective function.

The algorithm starts at an initial state and follows arrows to explore neighboring states in search of the highest peak.

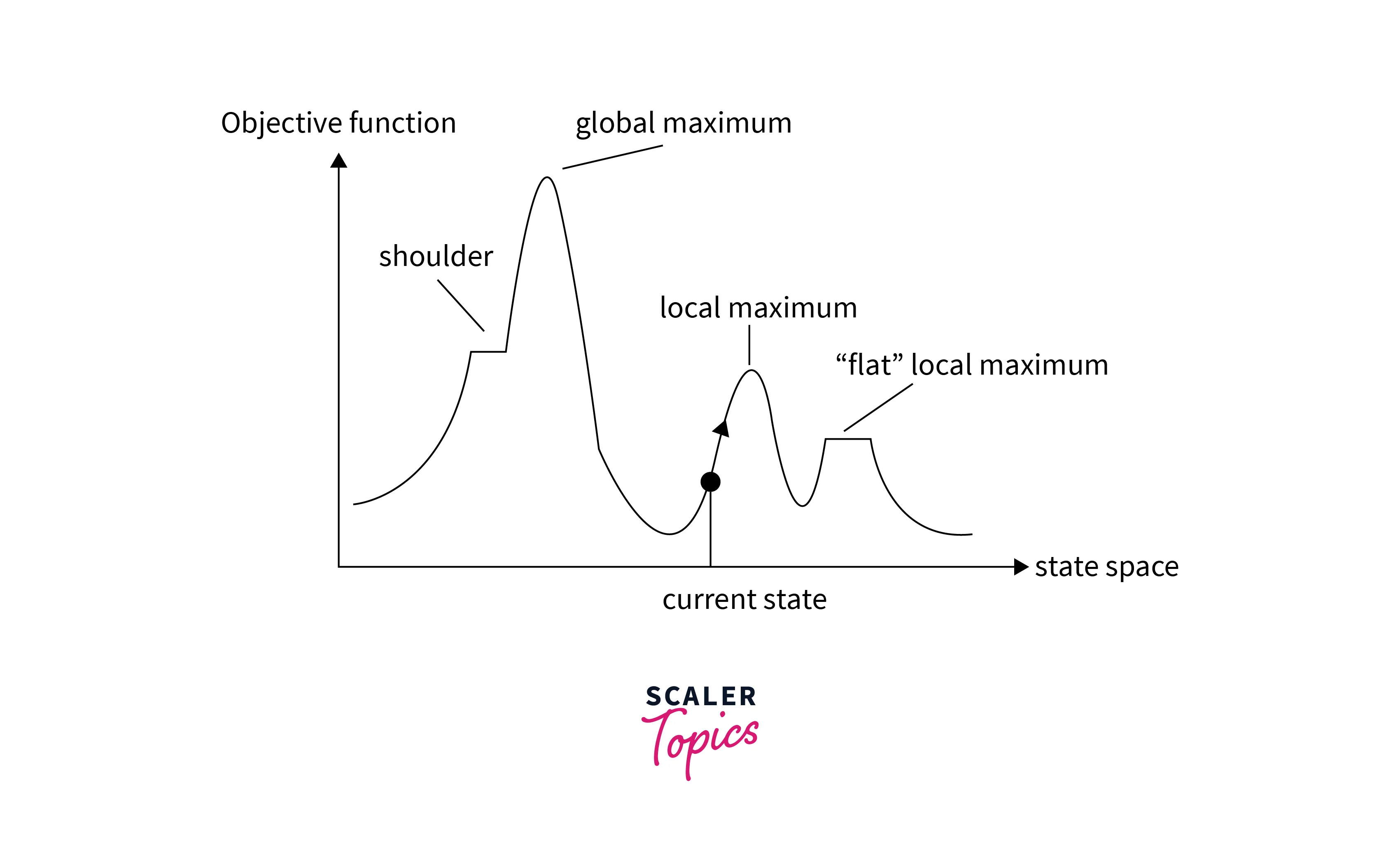The X-axis represents the potential states or configurations that our algorithm can attain. Meanwhile, the Y-axis represents the respective values of the objective function associated with each state.

Different Regions in the State Space Diagram

Here's an in-depth explanation of the various regions in the state space diagram:

1. Local Optima:

• Definition: Local optima are points in the state space where the objective function has a high value (in maximization problems) or a low value (in minimization problems), and these points are surrounded by solutions with lower in maximization or higher in minimization values of the objective function.
• Characteristics: Hill Climbing often encounters local optima. When the algorithm reaches a local optimum, it perceives no direction of movement that would lead to a better solution. Consequently, it tends to terminate, unaware of the existence of higher-quality solutions in other parts of the solution space.
• Challenge: Getting trapped in local optima is one of the primary challenges in Hill Climbing, particularly in complex landscapes with multiple peaks.

2. Plateaus:

• Definition: Plateaus are flat regions in the state space where the objective function remains constant over a range of solutions. In other words, many neighboring solutions have nearly identical objective function values.
• Characteristics: Plateaus can significantly slow down the Hill Climbing algorithm's progress. Since there's no discernible gradient, it may take a large number of iterations for Hill Climbing to move off a plateau and make significant progress.
• Challenge: Plateaus can be challenging because they make it difficult for the algorithm to distinguish between better and worse solutions when they have nearly identical objective function values.

3. Ridges:

• Definition: Ridges are narrow, elevated paths in the state space diagram that lead to higher regions. These paths typically have a higher objective function value than the surrounding solutions.
• Characteristics: Ridges can be challenging for Hill Climbing. If the algorithm starts on a ridge, it may oscillate back and forth along the ridge without making substantial progress toward the peak of the ridge or moving away from it.
• Challenge: Navigating ridges efficiently is a challenge for Hill Climbing because it requires careful step size adjustments or considering a more extensive set of neighbors.

4. Global Optimum:

• Definition: The global optimum is the highest point (in maximization problems) or the lowest point (in minimization problems) in the state space, representing the best possible solution for the optimization problem.
• Characteristics: The global optimum is the ultimate goal in most optimization problems. It represents the highest quality solution achievable.
• Challenge: The primary challenge for Hill Climbing is to find the global optimum, especially in problems with complex landscapes. The algorithm's tendency to get stuck in local optima can prevent it from reaching the global optimum.

Problems in Different Regions in Hill Climbing Algorithm

• The most common issue in Hill Climbing, is getting stuck in local optima. In a local optimum, the algorithm perceives no direction of improvement, as all neighboring solutions have worse objective function values. It terminates, assuming it has found the best solution.
• Plateaus are flat regions in the solution space where the objective function remains constant over a range of solutions. Hill Climbing struggles on plateaus because it can't discern the direction of improvement.
• Ridges are elevated paths in the solution space that may not lead directly to a peak but offer better objective function values than the surrounding solutions. Hill Climbing can oscillate along ridges without significant progress.

Applications of Hill Climbing Algorithm

The hill climbing algorithm finds applications in various domains within artificial intelligence and optimization:

1. Machine Learning: Hill climbing can be used for hyperparameter tuning in machine learning algorithms, finding the best combination of hyperparameters for a model.
2. Robotics: In robotics, hill climbing can help robots navigate through physical environments, adjusting their paths to reach a destination.
3. Network Design: It can be used to optimize network topologies and configurations in telecommunications and computer networks.
4. Game Playing: In game playing AI, hill climbing can be employed to develop strategies that maximize game scores.
5. Natural Language Processing: It can optimize algorithms for tasks like text summarization, machine translation, and speech recognition.