How to Check Divisibility by 7

Given a number N, we are supposed to check if it is divisible by 7 or not. Here, we are not supposed to use the modulo operator or floating point arithmetic. This can be done with the help of a recursive method.

There are various ways to get the desired result. Initially, we may think of dividing the number with 7 and getting the remainder. This facility is provided by the modulo function and we are not supposed to use that. Another method will be simply dividing the number with 7 and getting a floating point value but that is also against the given conditions.

Implementing code for such mathematical concepts improves our logical reasoning, and problem-solving and will help us in the future when we will be challenged to think of solutions for comparatively complex problems.

Approach

One of the brute force approaches we can think of is subtracting 7 from the number until we get the result less than or equal to 0. If the value becomes zero we can say that the original number was divisible by 7.

However, for large values, this method can be very time-consuming. Therefore, we need to find a more optimal solution. One of the popular methods is to represent the number in the form of 10a + b and if a - 2b is divisible by 7 then the given number is also divisible by 7.

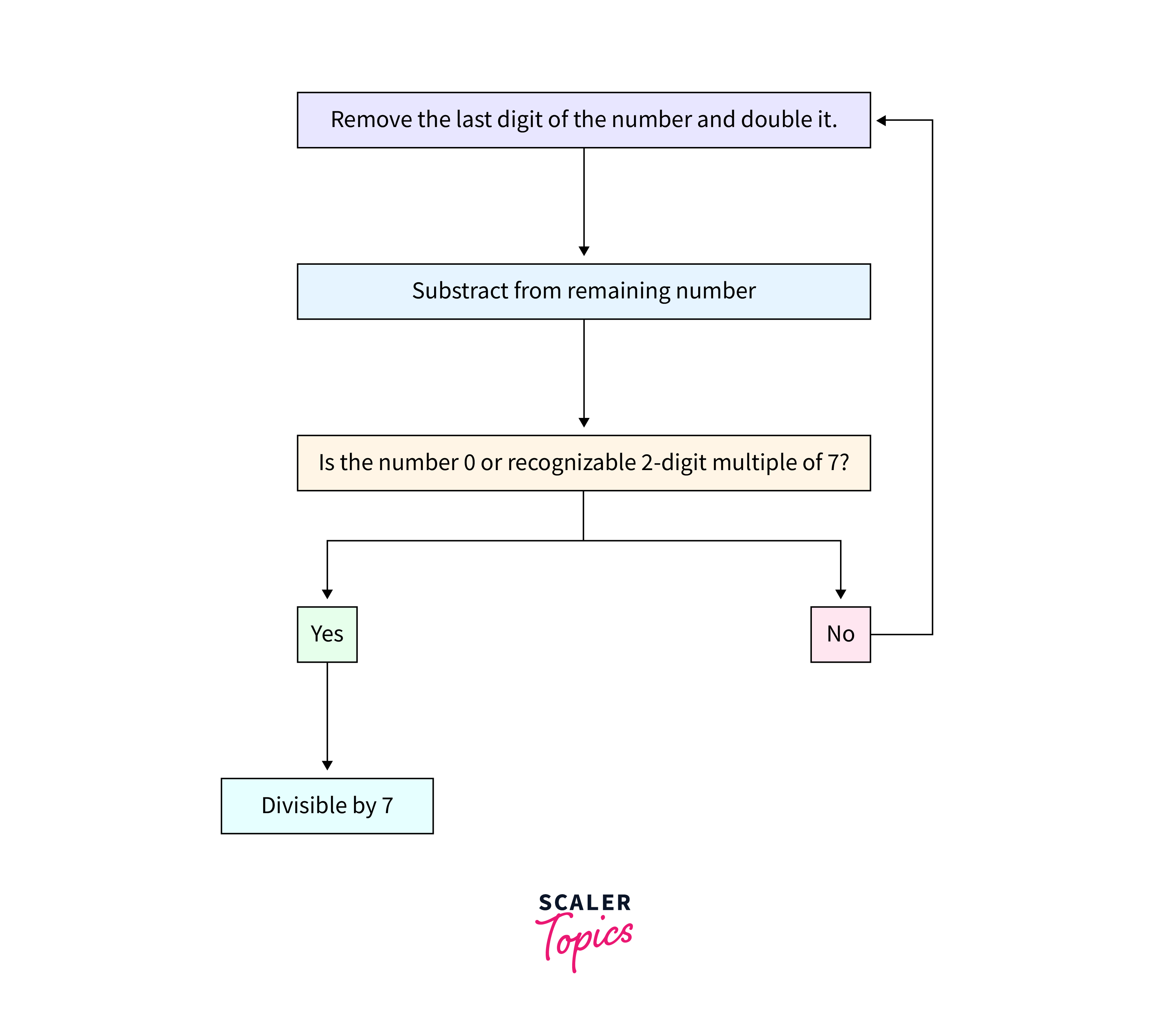
The approach is straightforward, the given number is a 10a + b. Now, if a - 2b is divisible by 7 then, only 10a + b is divisible by 7. This can be recursively called or iteratively checked until we end up with a 7, or a 0.

Let us break down the above procedure into steps:

1. Find the digit at the unit's place from the rest of the number N and say b. This can be done by taking modulo with 10. Note that we cannot use modulo with 7 to get the remainder.
2. Next, we will divide the given number N by 10 and call it a.
3. Now multiply b with 2 and subtract this from a.
4. If the result is greater than 9 then repeat the above 3 steps until the number is less than 9.
5. If the number is less than 9 and not equal to 0 or 7 then we will return true else return false.
6. Sometimes the resultant number is negative but still divisible by 7. Thus we will also check if the number is equal to -7 or -14 which are also divisible by 7.

Example

Let us take a few examples and also dry run the above method to check if the number is divisible by 7 or not.

Example 1

• INPUT: 371
• CONDITION: 371 > 9 => TRUE
• UPDATE:
  • a = 37, b = 1
  • a - 2b = 37 - 2 = 35 = num
• CONDITION: 35 > 9 => TRUE
• UPDATE:
  • a = 3, b = 5
  • a - 2b = 3 - 10 = -7 = num, LOOP BREAKS
• CONDITION: num == -7 => TRUE
• OUTPUT: The given number is divisible by 7.

Example 2

• INPUT: 559944
• CONDITION: 559944 > 9 => TRUE
• UPDATE:
  • a = 55994, b = 4
  • a - 2b = 55994 - 8 = 55986 = num
• CONDITION: 55986 > 9 => TRUE
• UPDATE:
  • a = 5598, b = 6
  • a - 2b = 5598 - 12 = 5586 = num
• CONDITION: 5586 > 9 => TRUE
• UPDATE:
  • a = 558, b = 6
  • a - 2b = 558 - 12 = 546 = num
• CONDITION: 546 > 9 => TRUE
• UPDATE:
  • a = 54, b = 6
  • a - 2b = 54 - 12 = 42
• CONDITION: 42 > 9 => TRUE
• UPDATE:
  • a = 4, b = 2
  • a - 2b = 4 - 4 = 0
• CONDITION: 0 > 9 => FALSE, LOOP BREAKS
• CONDITION: num == 0 => TRUE
• OUTPUT: The given number is divisible by 7.

Example 3

• INPUT: ``
• CONDITION: 52 > 9` => TRUE
• UPDATE:
  • a = 5, b = 2
  • a- 2*b = 5 - 4 = 1` = num
• CONDITION: 1 > 9 => FALSE, LOOP BREAKS
• CONDITION: 1 != 7 || 1 != -7 || 1 != -7 || 1 != 0 || 1 != -14 => FALSE
• OUTPUT: The given number is not divisible by 7.

Implementation

Complexity Analysis

We can also perform this recursively, in that case, the space complexity will be O(log n) but since we are using iteration to save space the space complexity is O(1). Time complexity is O(n) for the above program.

Time Complexity: O(log n)

Auxiliary Space: O(log n)