C Program to Convert Infix to Postfix Expression Using Stack

Infix expressions feature operators between operands, like 'a + b,' whereas postfix expressions place operators after operands, as in 'ab+.' This article elucidates the conversion process from infix to postfix notation using C programming. While infix denotes operations like 'x + y,' postfix rearranges them to 'xy+', streamlining expressions by positioning operators to the right of operands, facilitating efficient computation and code interpretation in languages like C.

Let us consider an example, if we have this form of expression, then these notations facilitate us in restructuring the logic in several fashions.

It is important to emphasize that the values calculated after evaluation do not vary in these different notations, but the way the expression is interpreted changes.

Infix Expression

This is more human-readable and generally used by humans for better understanding, In this representation, the operator remains in the middle and operand exists on both sides of the operator and the value can be evaluated simply according to precedence and associativity rule.

Structure:

Example:

Explanation:

5 + 4 * (9 - 2) = 5 + 4 * 7 = 5 + 28 = 32

Postfix Expression

In this notation, the operator remains on the right side of both operands like this,

Structure:

Example:

Explanation:

We can consider the expression (4 9 2 - *) before the last operator as one operand and the first (5) as another operand. Solving the expression recursively, 5 4 9 2 - * + = 5 4 7 * + = 5 28 + = 32

Prefix Expression

Similar to the last one, in this notation the operator is on the left side of both operands like this,

Structure:

Example:

Explanation:

Wthe operands for first + operator are, 5 and *4-92. This can be solved by reading the expression from right to left.

+ 5 * 4 - 9 2 = + 5 * 4 7 = + 5 28 = 32

Algorithm to Convert Infix to Postfix Expression Using Stack

If we are converting our Infix Notation to any other notation then there should be a predefined and standard approach to follow so, here we will discuss the exact algorithm with an example to explain how the transformation occurs. The Infix Notation is traversed from left to right and a stack is used here to maintain the operator to be inserted in the postfix expression.

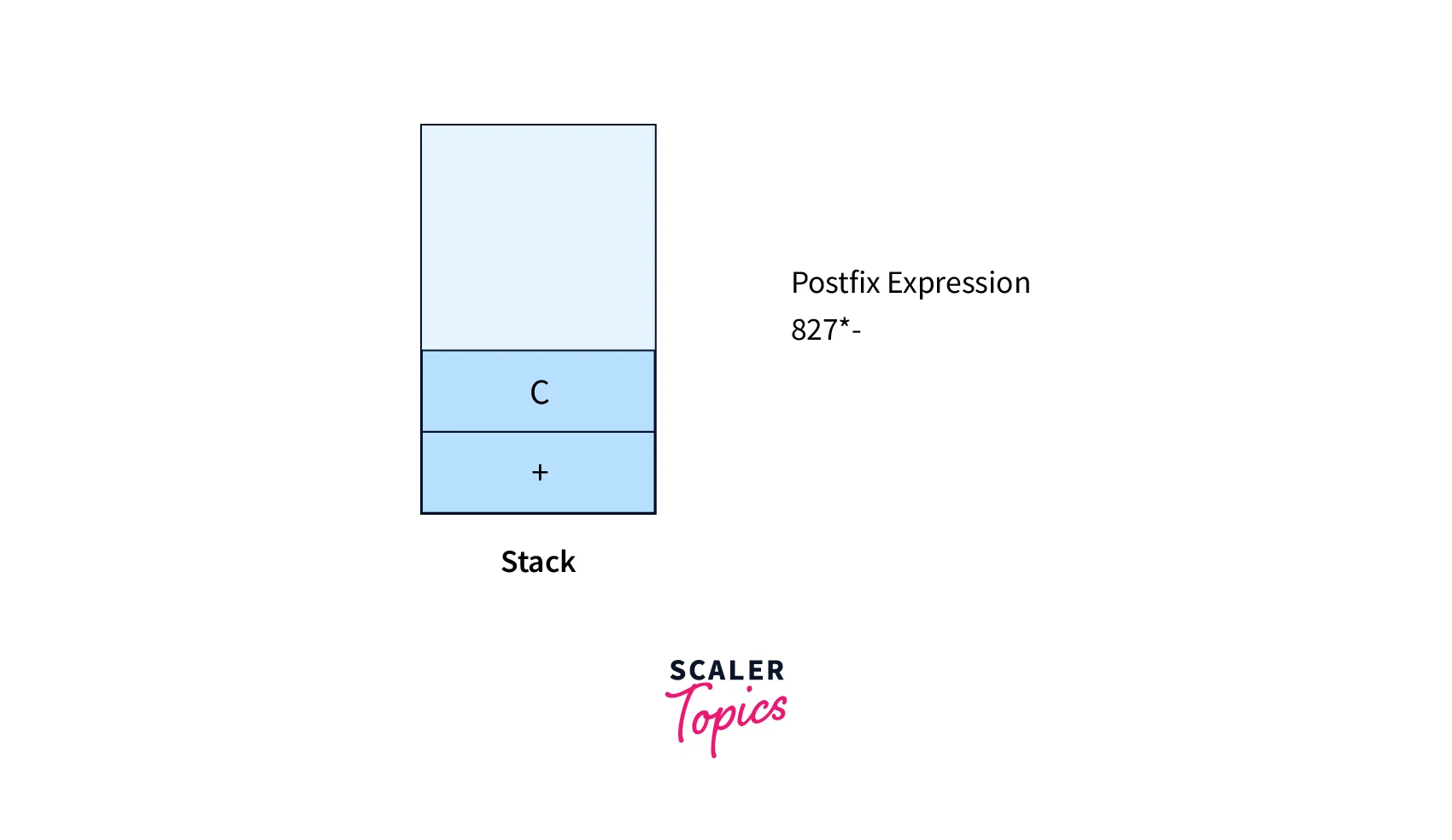
1. If we encounter an opening parenthesis (, we push it into the stack.
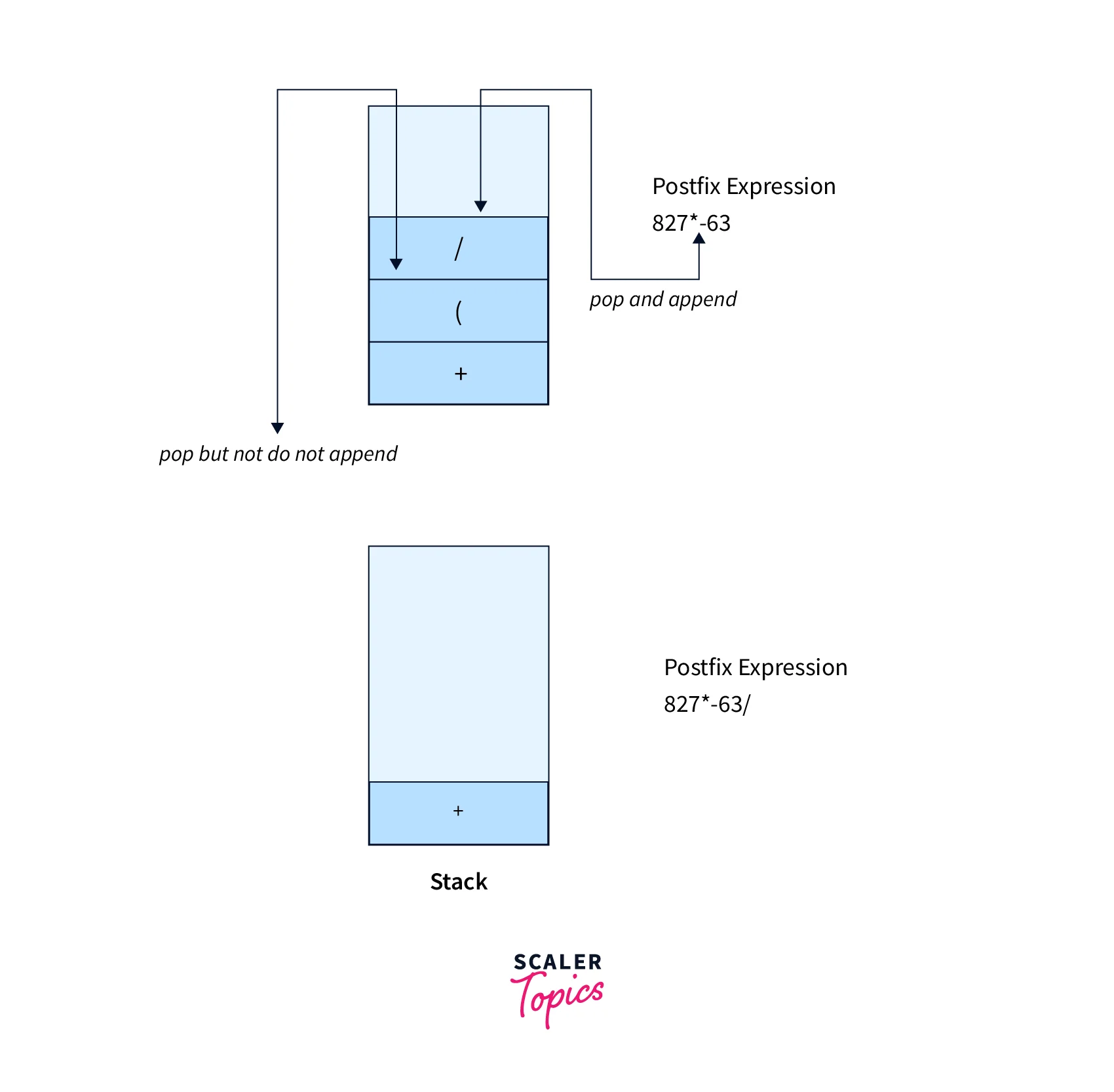
2. If we have a closing parenthesis ), then keep popping out elements from the top of the stack and append them to the o postfix expression until the top of the stack contains (. In the end, just pop out the opening parenthesis but make sure to not append this in the postfix expression.
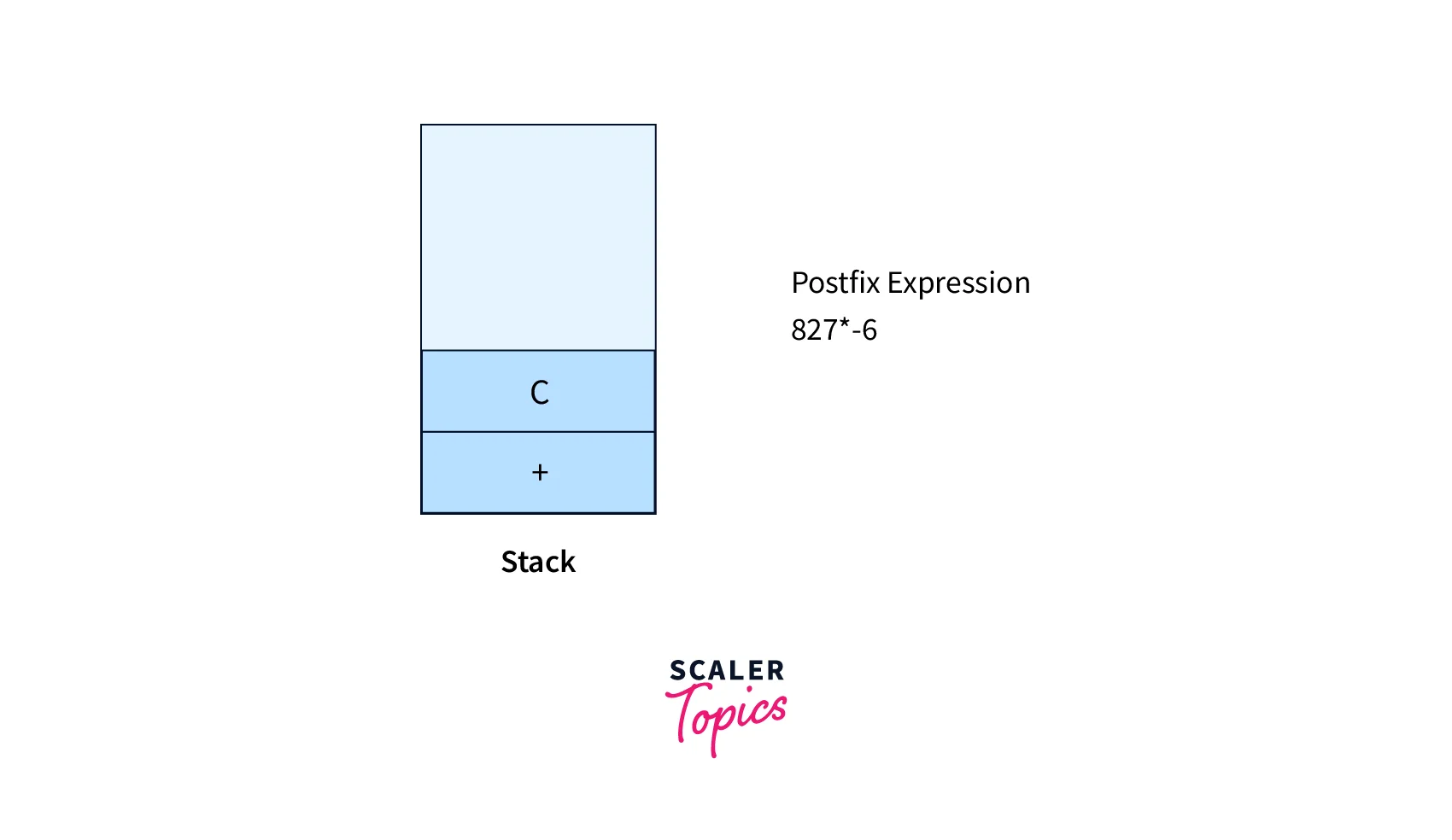
3. If we encounter an operand, then append it to the postfix expression.
4. If we encounter any operator, then exist exists several cases,
   • If the top of the stack contains the operator with less precedence in comparison to the operator which is going to be pushed there or stack is empty, then just push the new operator in the tack.
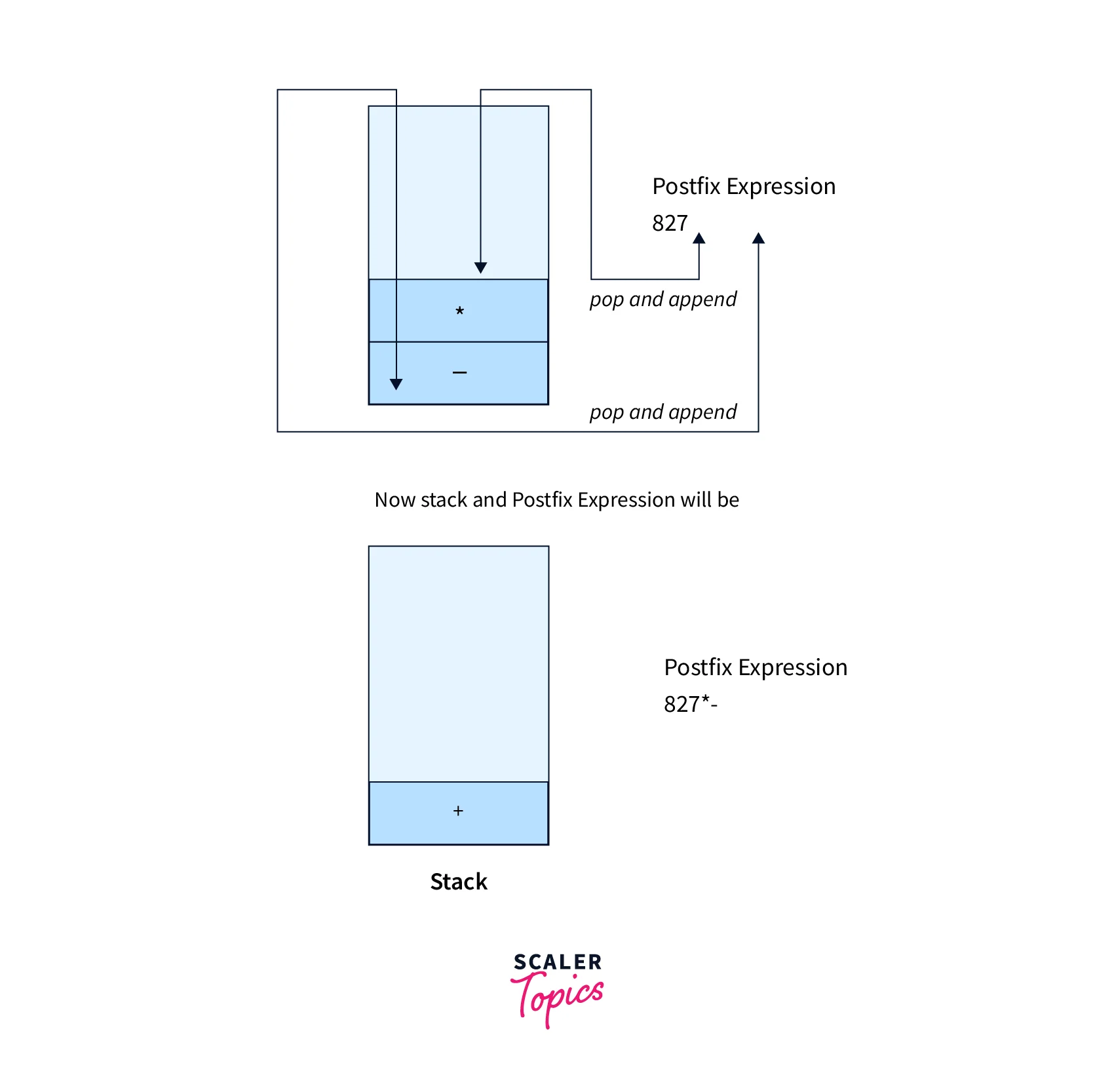
   • If the top of the stack contains the operator with high or equal precedence then pop the operators from the stack and append to the postfix expression until the top of the stack will not contain the operator with lower precedence.
   • Let's discuss informally just memorize this point to avoid confusion, so the inference of these two points is, that the operator which is at the upper level of the stack must have strictly higher precedence than the one which is at a lower level.
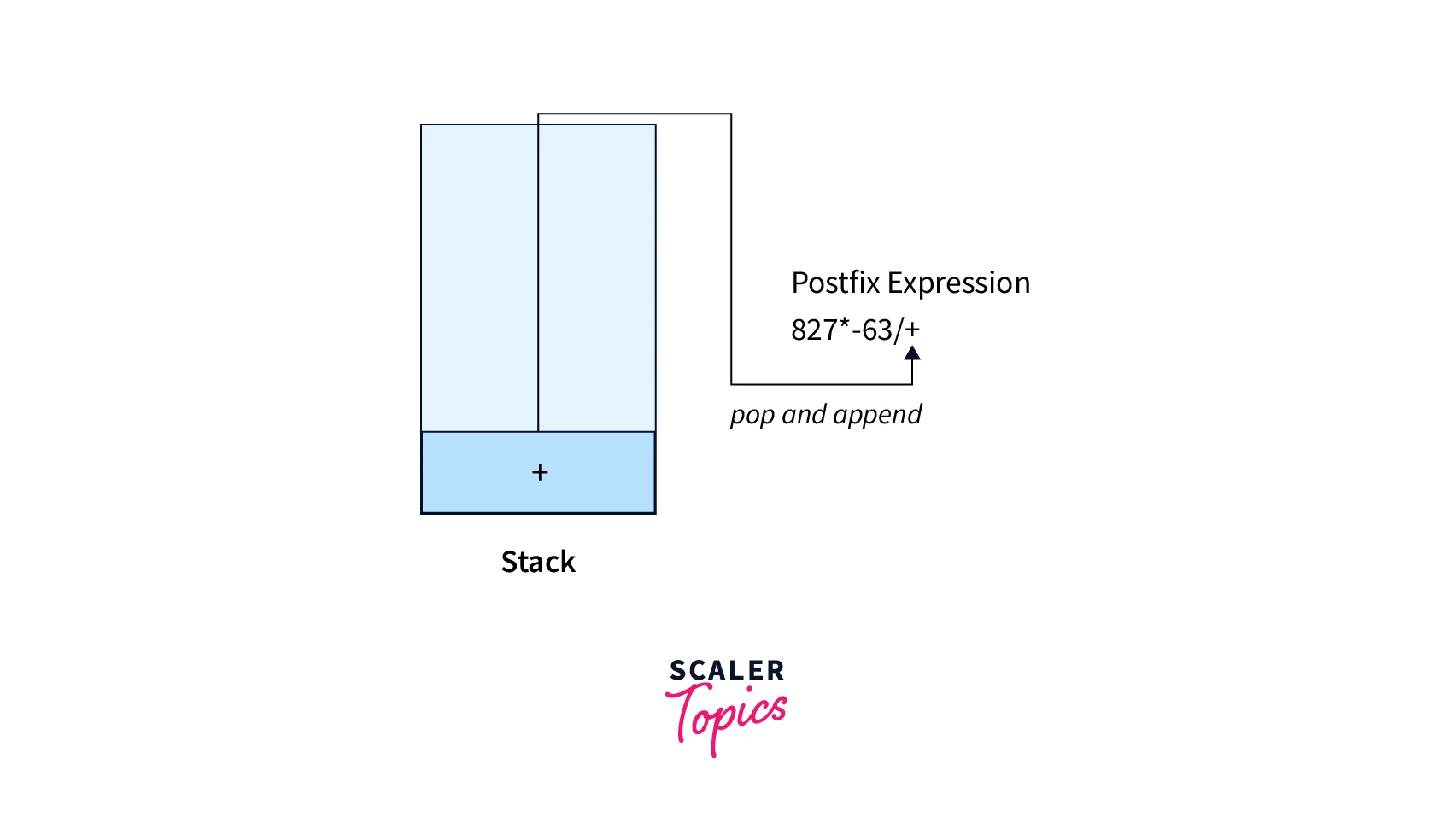
5. In the end if we have nothing to traverse in the Infix Notation then just append all operators from the stack in the sequence of pop operations.

Let's take an example to find out the postfix for the infix notation with the help of the algorithm written above. The first step is to start Scanning the Infix Notation from Left to Right and further follow the rules to get the required expression.

Infix:

1. Operand 8, hence apply Rule No. 3

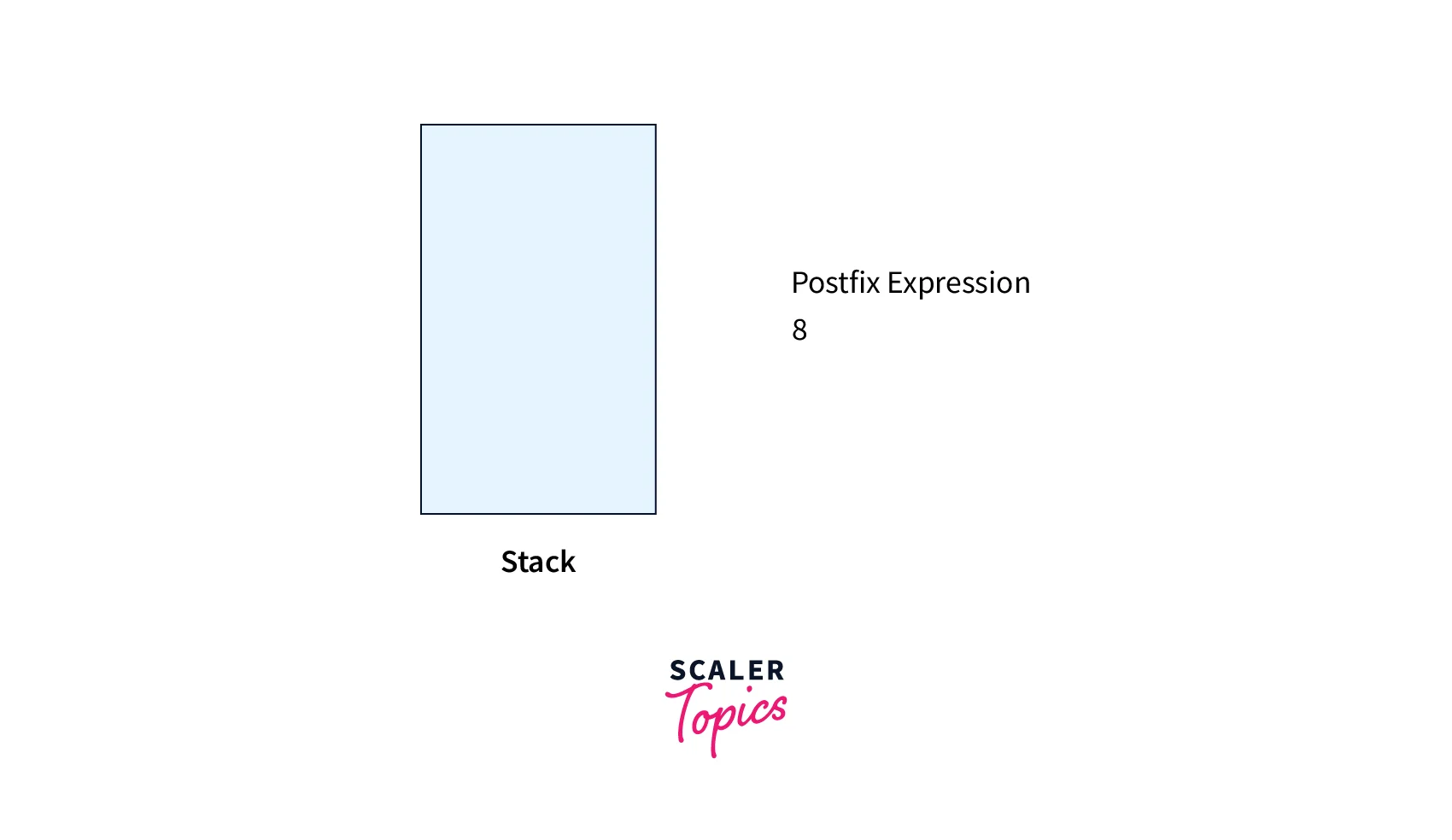
2. Operator -, hence apply Rule No. 4A

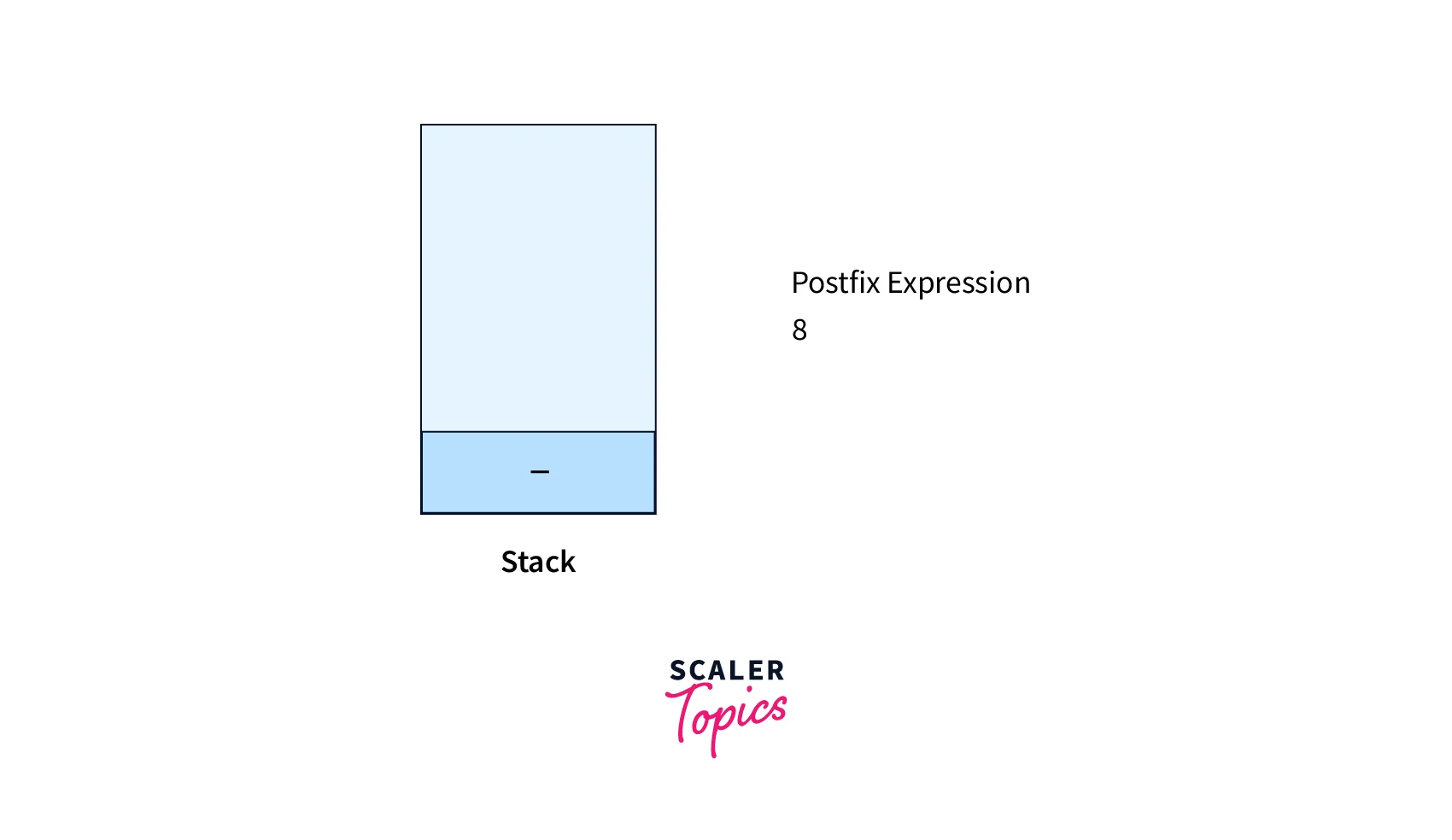
5. Operand 2, hence apply Rule No. 3

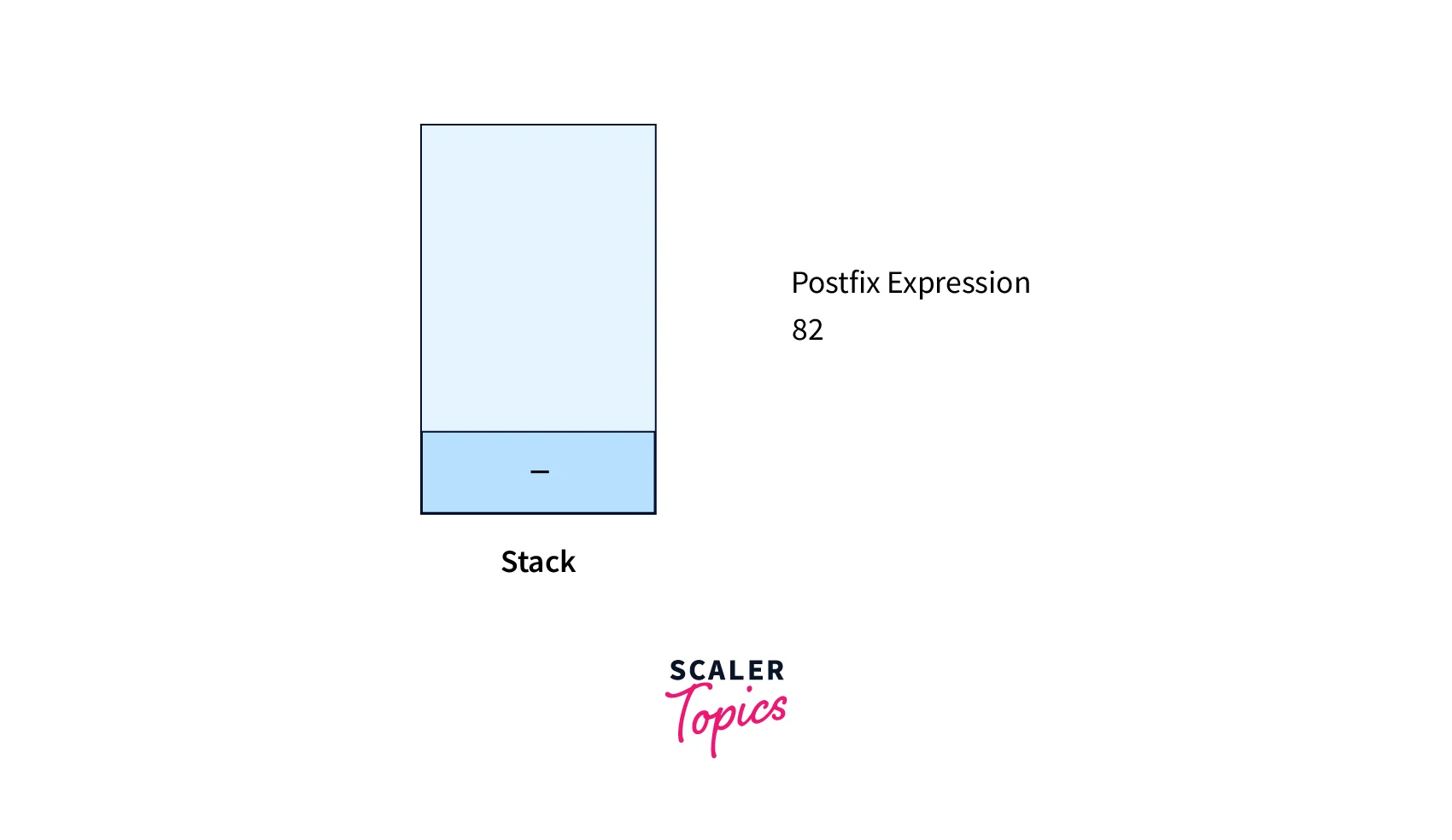
7. Operator *, hence apply Rule No. 4A

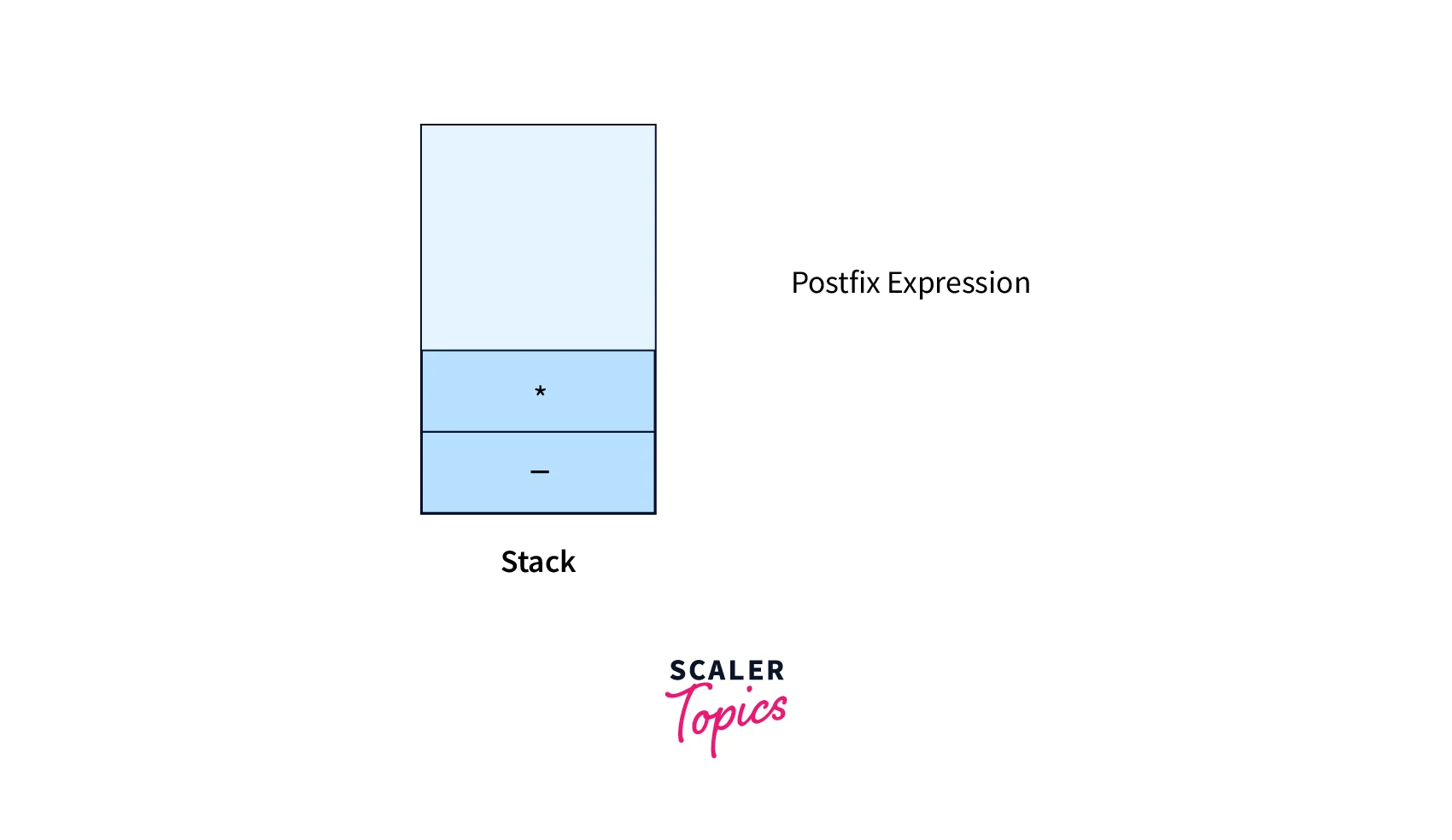
9. Operand 7, hence apply Rule No. 3

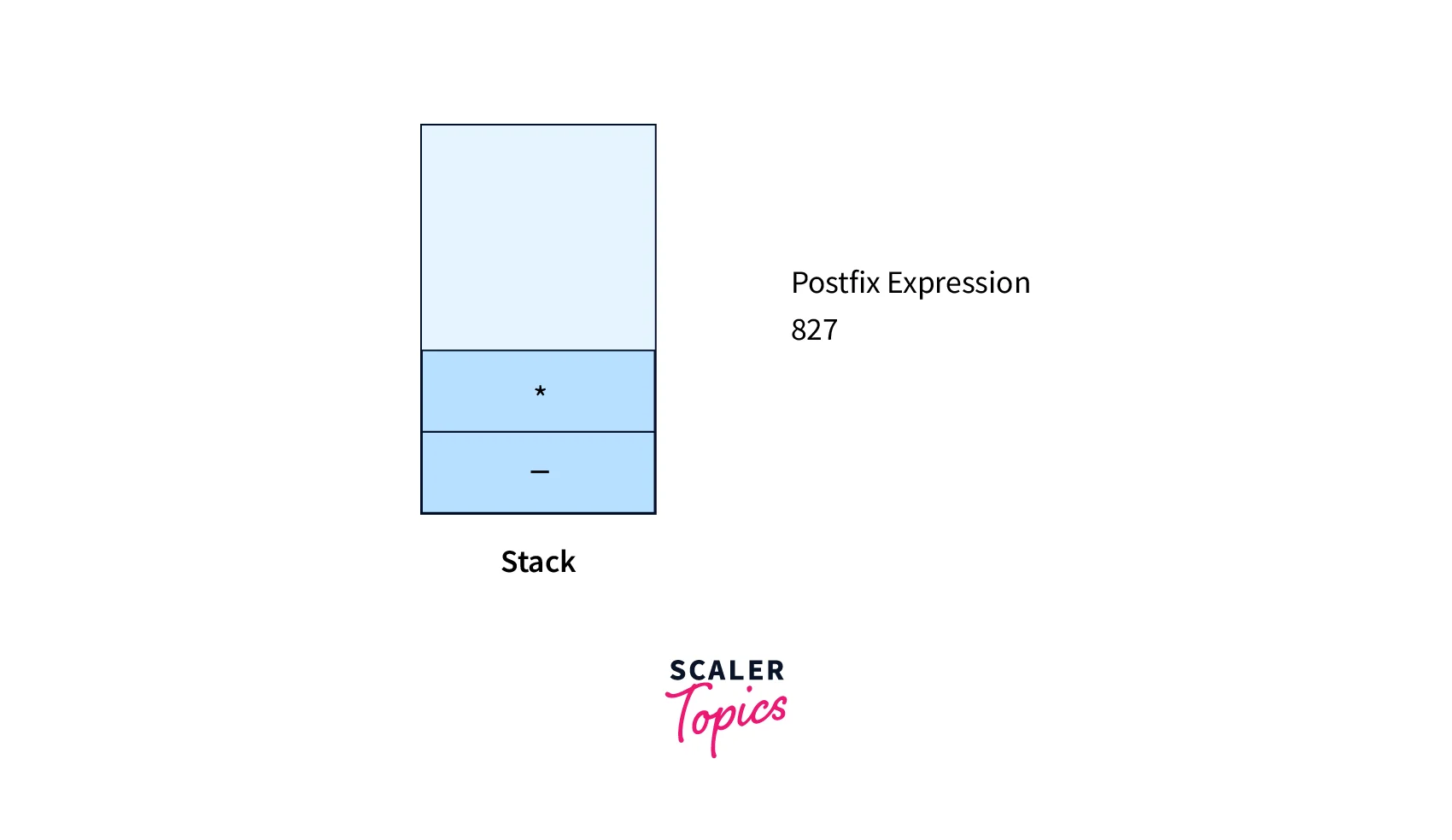
11. Operator +, hence apply Rule No. 4B

13. OpenParenthesisesis (, hence apply Rule No. 1

15. Operand 6, hence apply Rule No. 3

17. Operator /, hence apply Rule No. 4A

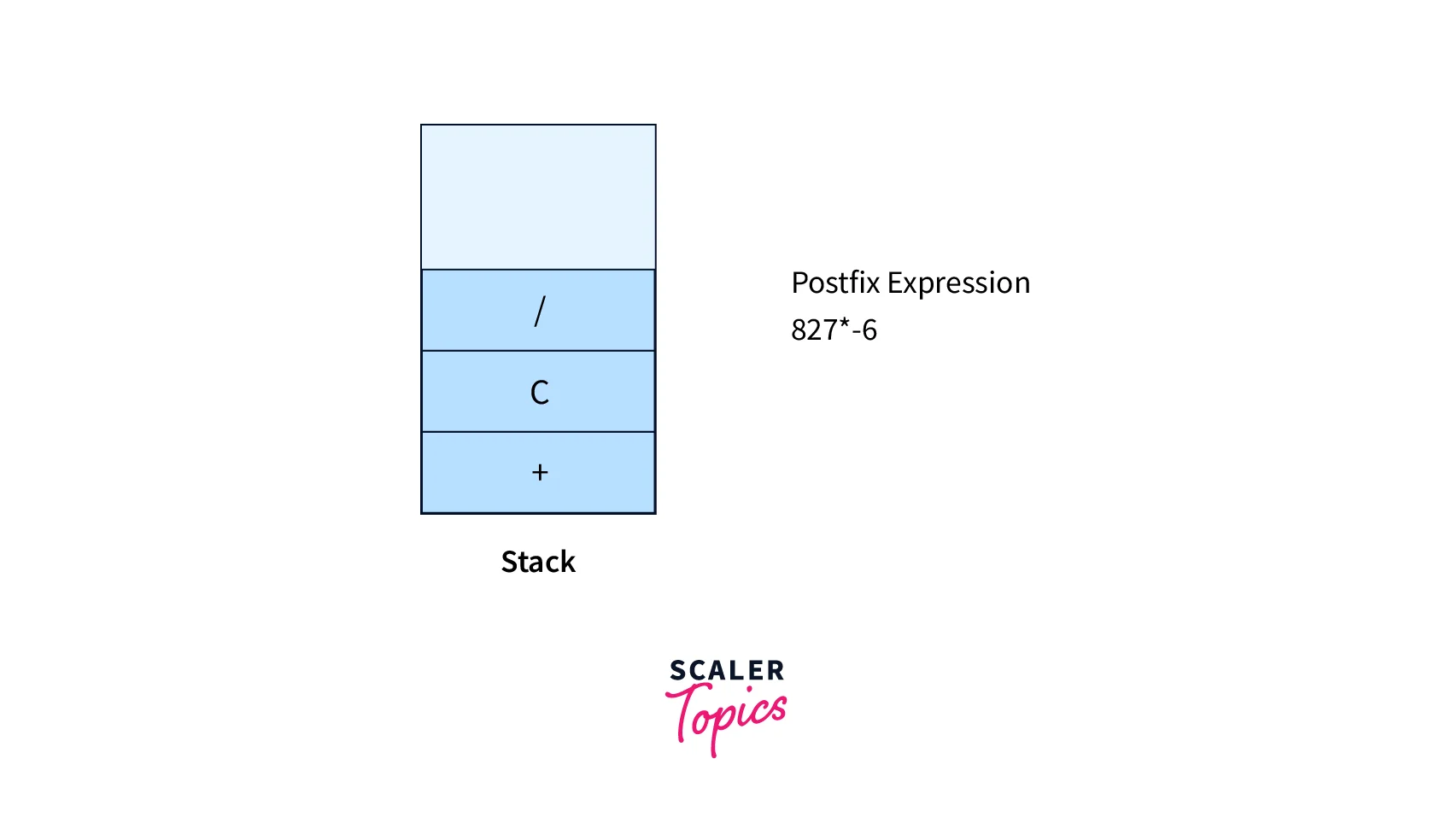
19. Operand 3, hence apply Rule No. 3

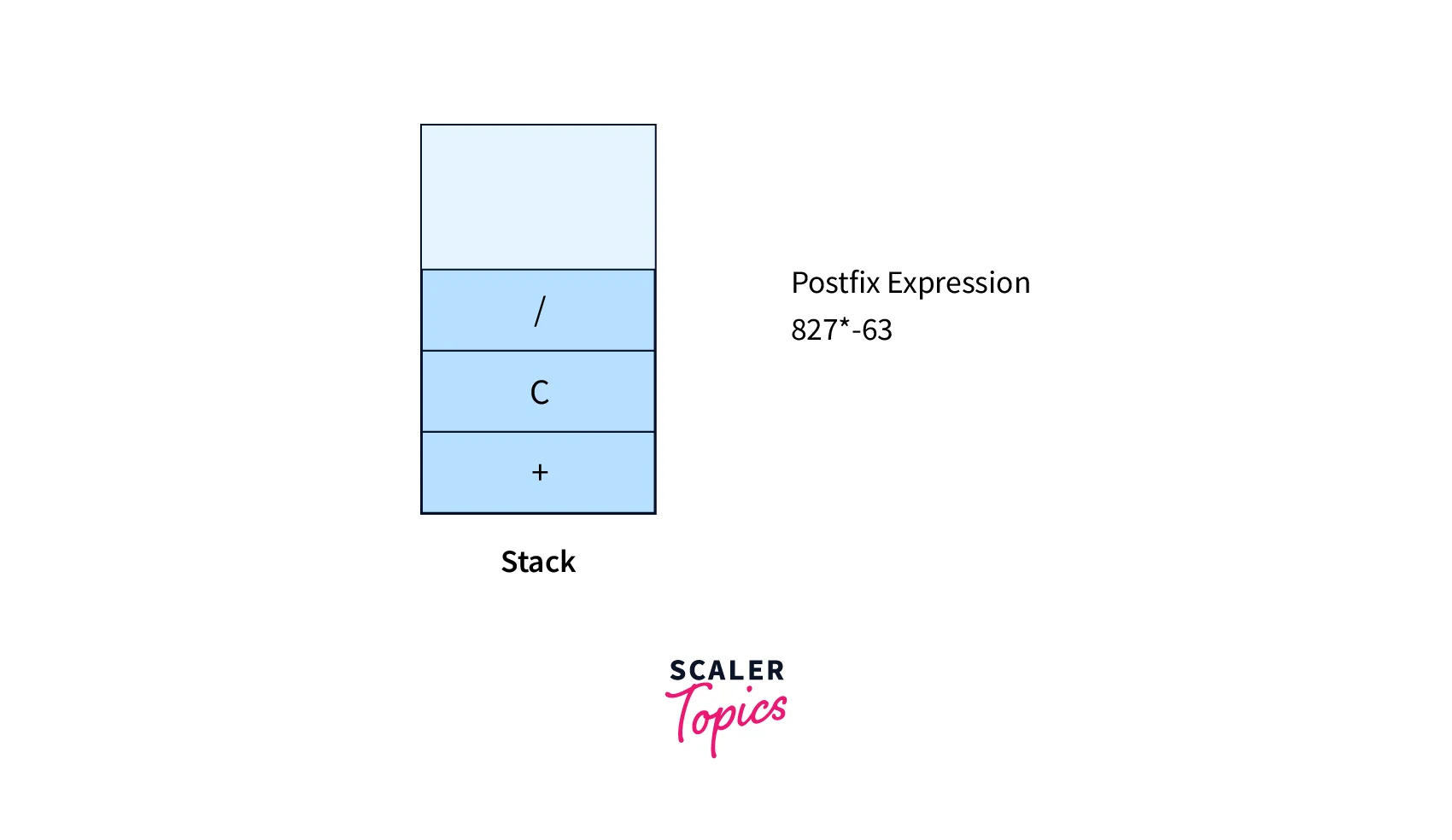
21. Closing Paranthesis ), hence apply Rule No. 2

23. Nothing Left in the Infix Notation, hence apply Rule No. 5

Postfix:

Implementation of the Algorithm for Infix to Postfix in the C Program

Following the algorithmic description, it is now time to implement the infix to postfix program in C. Because there is no built-in support for the stack in C language, we will explore two approaches to imitate the functionality of the stack: array and struct.

Method 1 ing array-based stack approach

Input 1:

Output 1:

Input 2:

Output 2:

Method 2: Using a struct based stack approach

There is not much difference between this method and the one demonstrated above, only the manner of allocating and accessing memory is changed for the implementation of infix to postfix program in C.

Input 1:

Output 1:

Input 2:

Output 2:

More Examples

Handling Mixed Brackets

We previously constructed an infix to postfix program in C that only works with parentheses; now we will modify our code to deal with several sorts of brackets such as {}, [], and parenthesis ().

Input 1:

Output 1:

Input 2:

Output 2:

Advantage of Postfix Expression over Infix Expression

You might be wondering why we are using this strange postfix expression, so here are a few reasons or can say advantages.

• Simplified and Parenthesis free Logic

When an infix expression is changed to a postfix expression, it no longer contains any parenthesis, and we have a predetermined mechanism to parse the expression, making it easily understandable by machines.

• Fast Parsing and Execution

The syntax tree is constructed while translating the source code to the actual target code to be executed on the machine, so the polish notation and reverse polish notation are parsed more readily than the han infix notation. This is why many interpreted and compiled programming languages make use of these notations.

• No ambiguity of Precedence and Associativity

When solving a sub-expression of postfix or prefix notation, it only requires two operands that can be found either before or after the operator, so the evaluation mechanism takes those operands and operator to evaluate the value without taking precedence and associativity into consideration because that was already done while converting the expression from Infix to Postfix.