Insertion Sort in C

Insertion Sort is a simple algorithm for sorting arrays. It divides the array into two parts: sorted and unsorted. Starting with the second element, each item is picked from the unsorted section and placed in its correct position in the sorted section. This is achieved by comparing the current element with the elements in the sorted section and shifting them if necessary to make space for the current element. The process continues until all elements are sorted. Unlike two separate arrays, this method sorts the array in place, minimizing memory usage. Insertion Sort is efficient for small arrays or nearly sorted arrays but becomes inefficient for larger datasets due to its time complexity of O(n^2).

Characteristics of Insertion Sort

• It is one of the simplest algorithms to sort an array. It is easy to understand and implement.
• It is efficient only for a small number of data values.
• Insertion sort is appropriate if the data is partially sorted, i.e. it is adaptive in nature.
• It follows an incremental approach, i.e. the number of elements in the sorted section of the array is increased one by one.
• It is a stable and in-place sorting algorithm.

Working of Insertion Sort Algorithm

Let us take an example of the array as follows: {45, 33, 2, 60, 71, 68} Initially, the array is as follows:

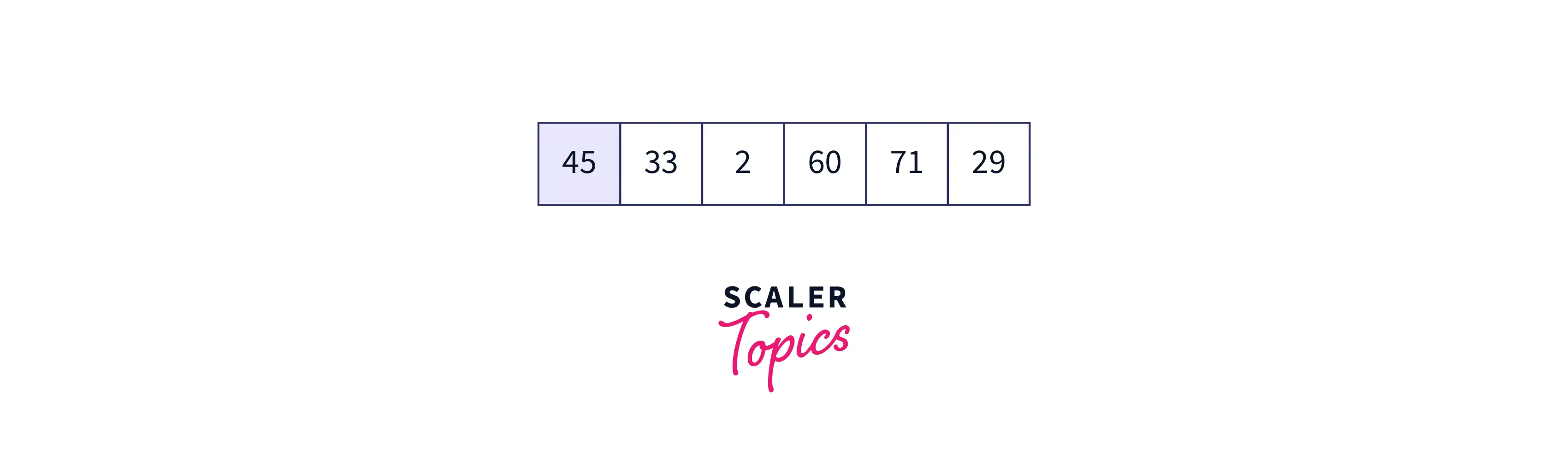
First iteration:

• Initially, the first element is sorted, and i points to the second element, i.e., 33. Now, j points to the 45. After running the while loop, j = -1, cur = 33, and the array is -

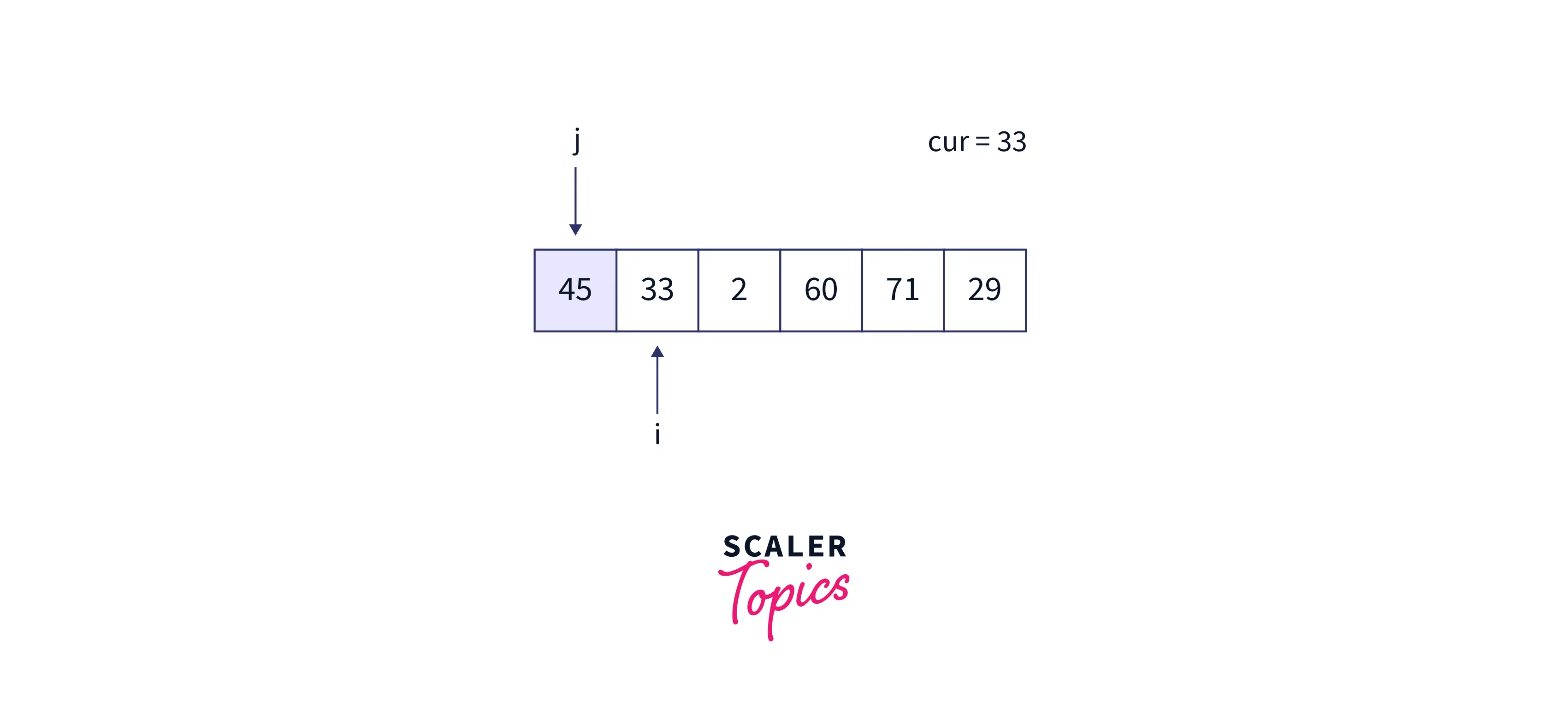
While Loop:

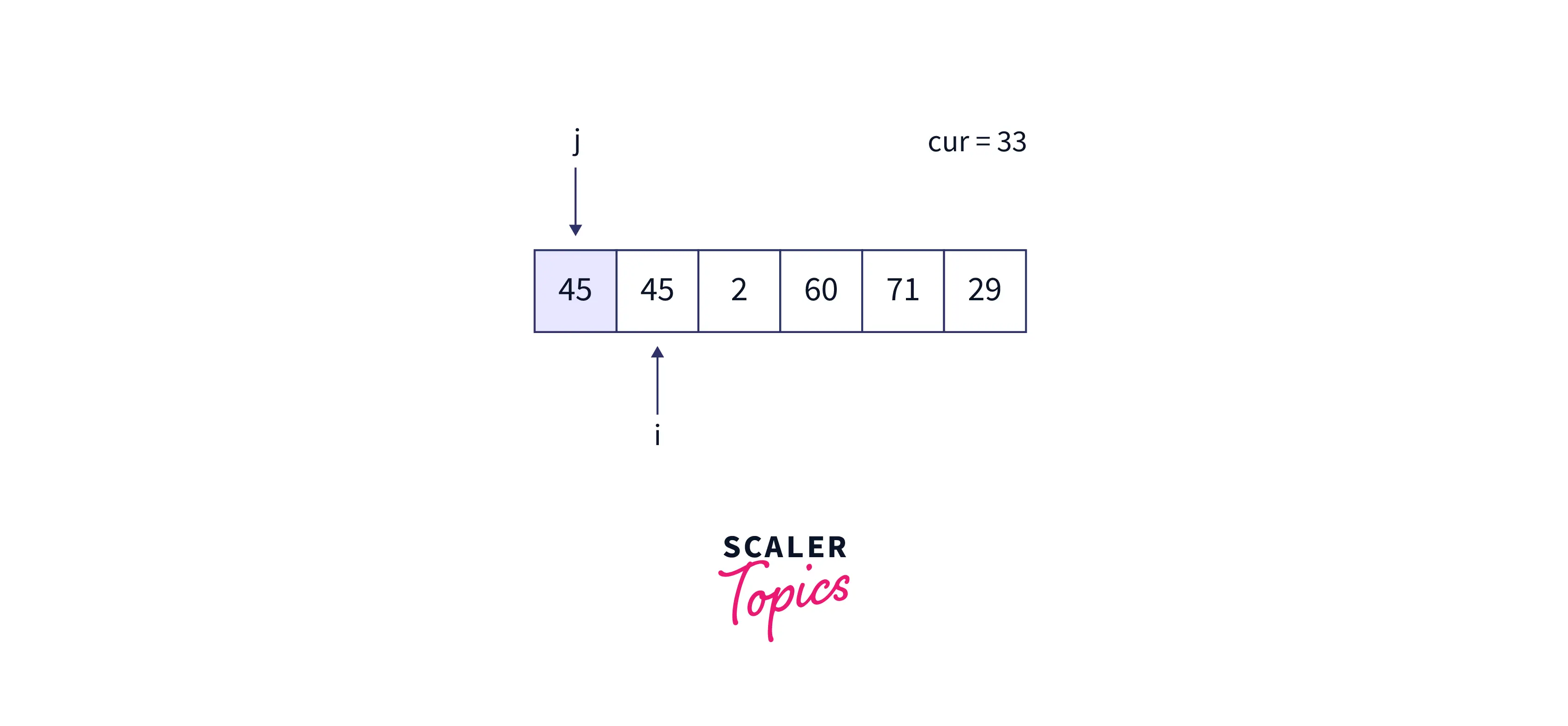
• At the end of for loops iteration, we place cur at its position, i.e. j+1 = 0, and the array becomes

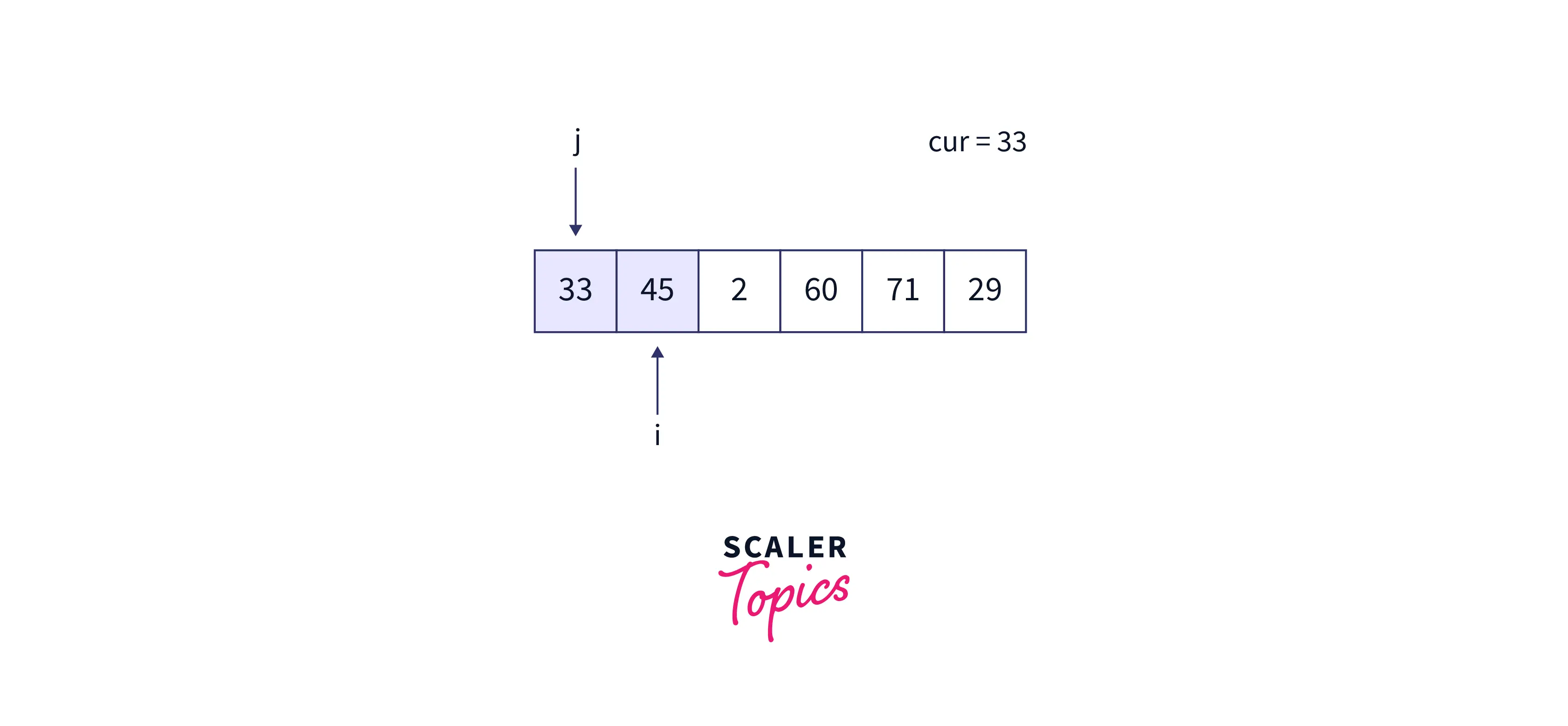
Second iteration:

• Now I point to 2, and j points to 33. After execution of the while loop

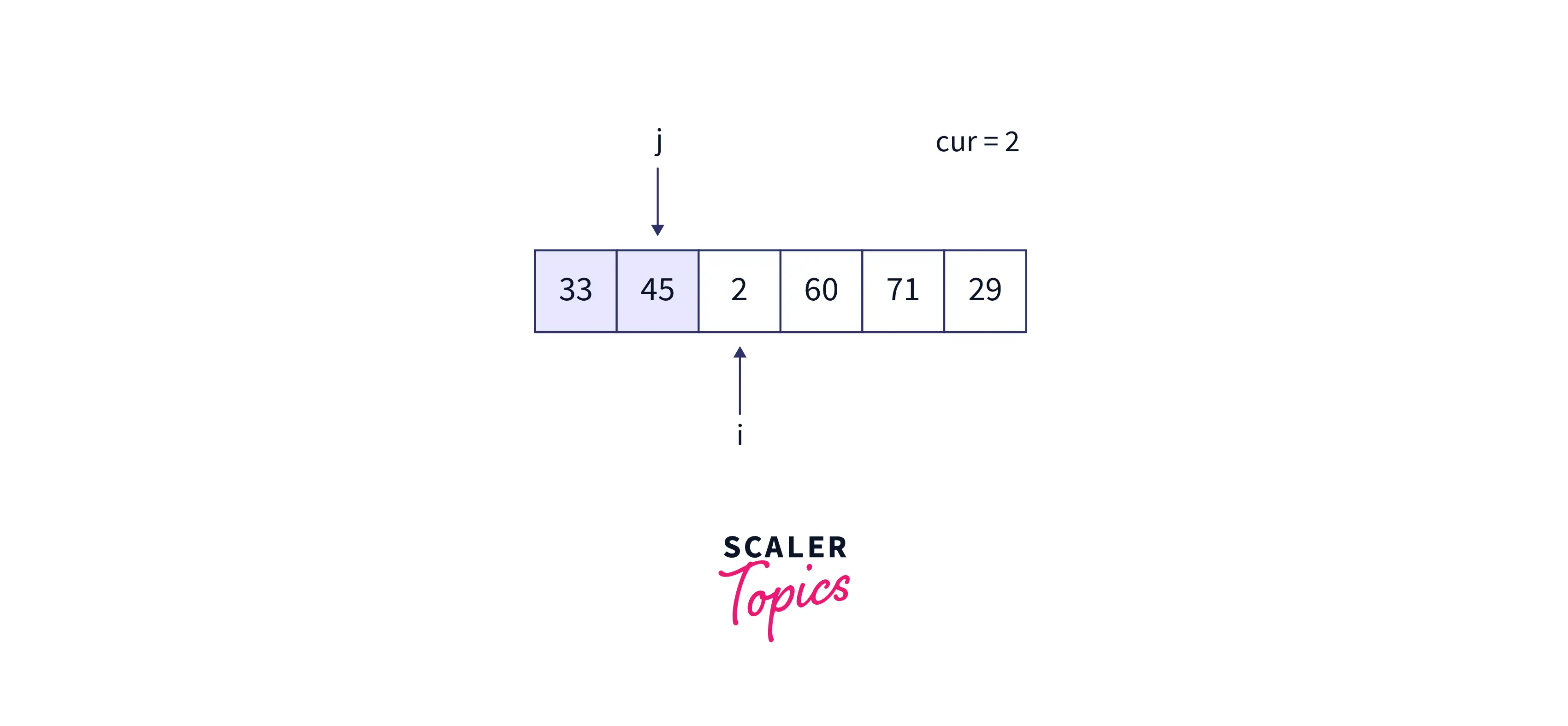
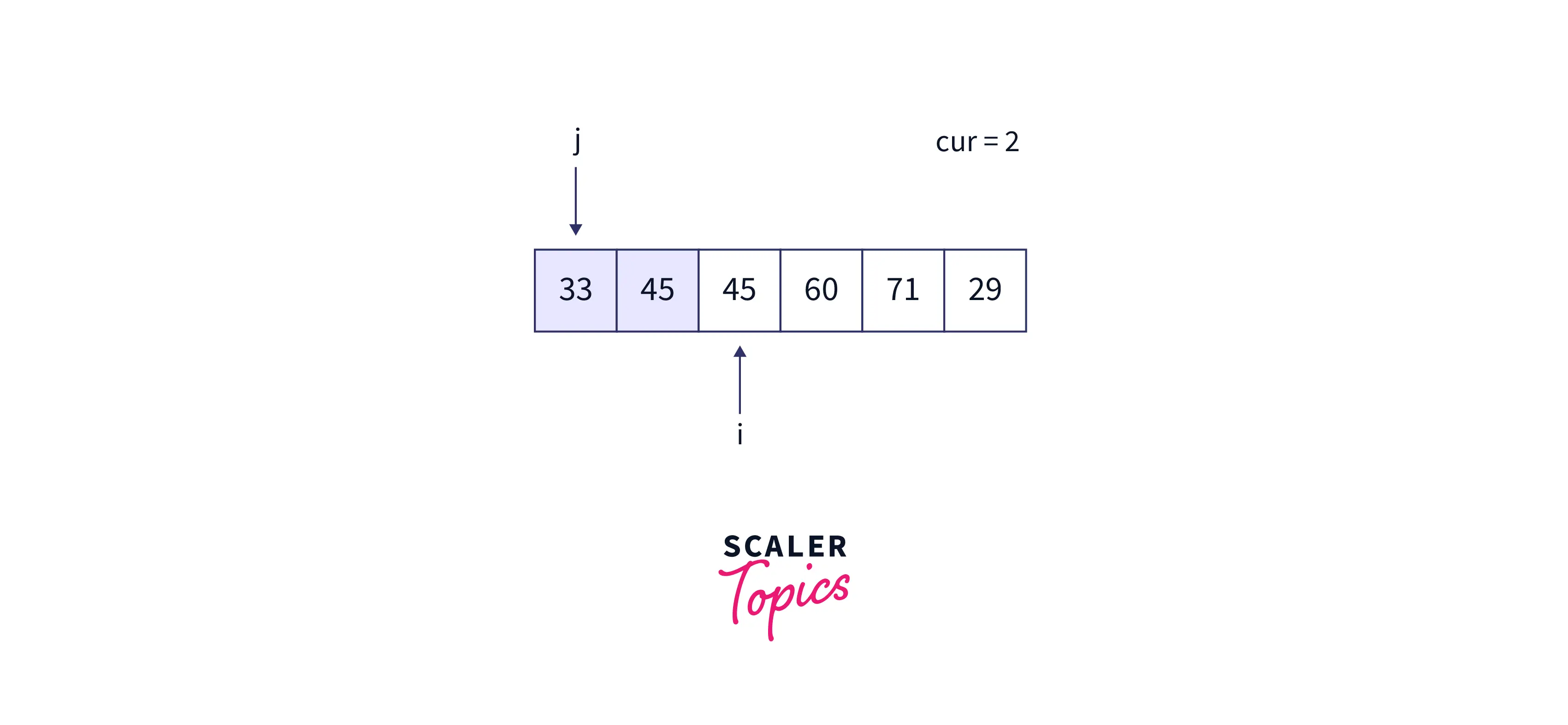
While Loop:

• arr[j] = cur

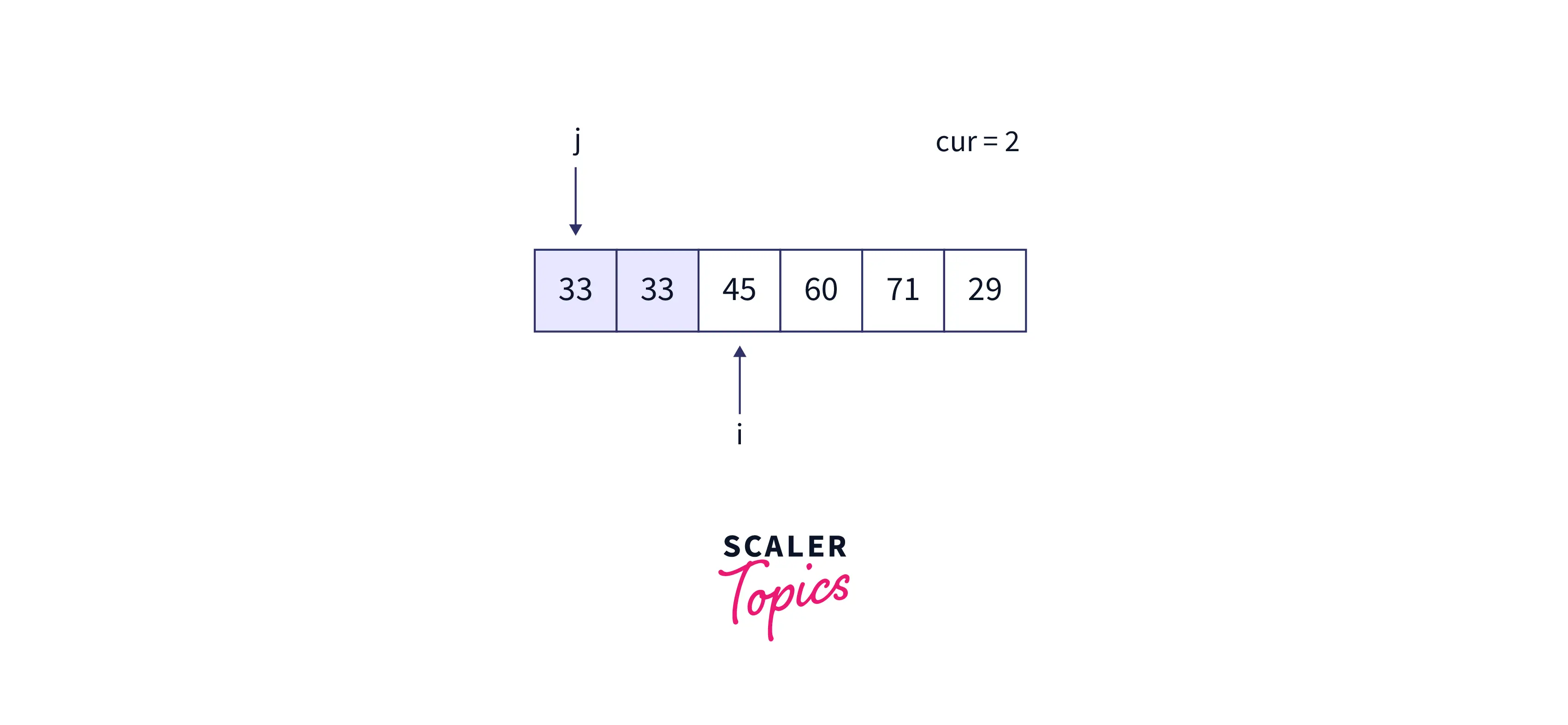
At the end of the second iteration, the array is as follows:

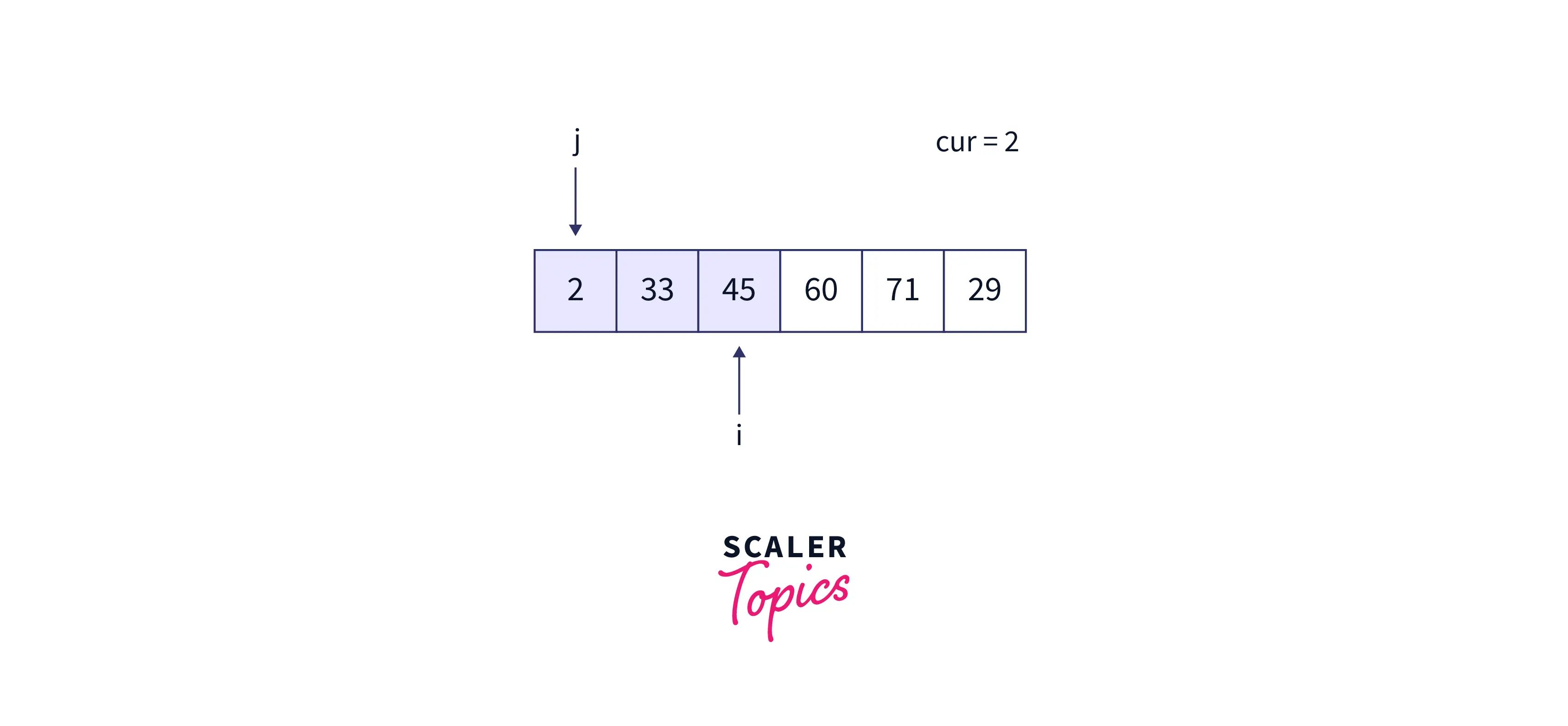
Third iteration: At the beginning of the third iteration,

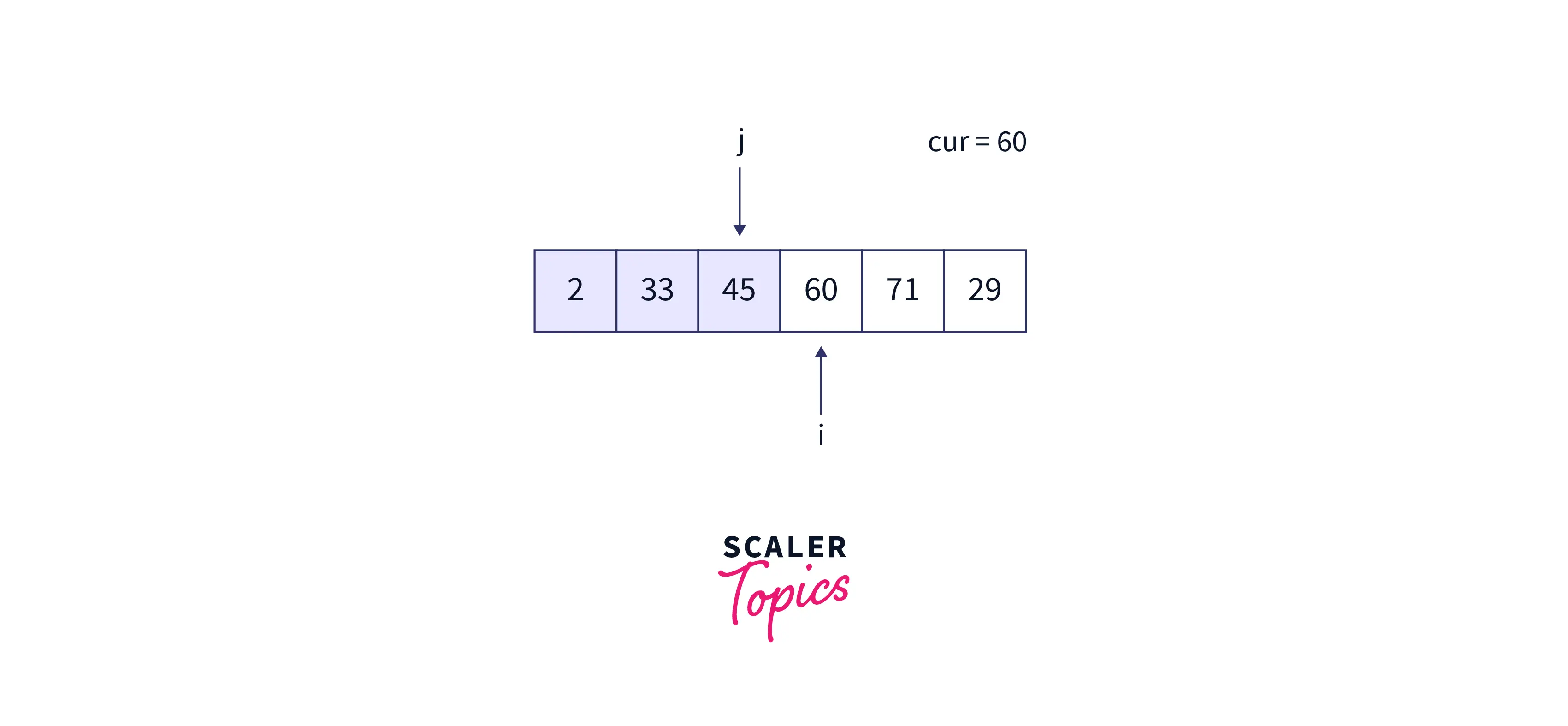
• cur = 60, j points to 45, and 60 is greater than 45; thus, we are not required to modify anything in this iteration.

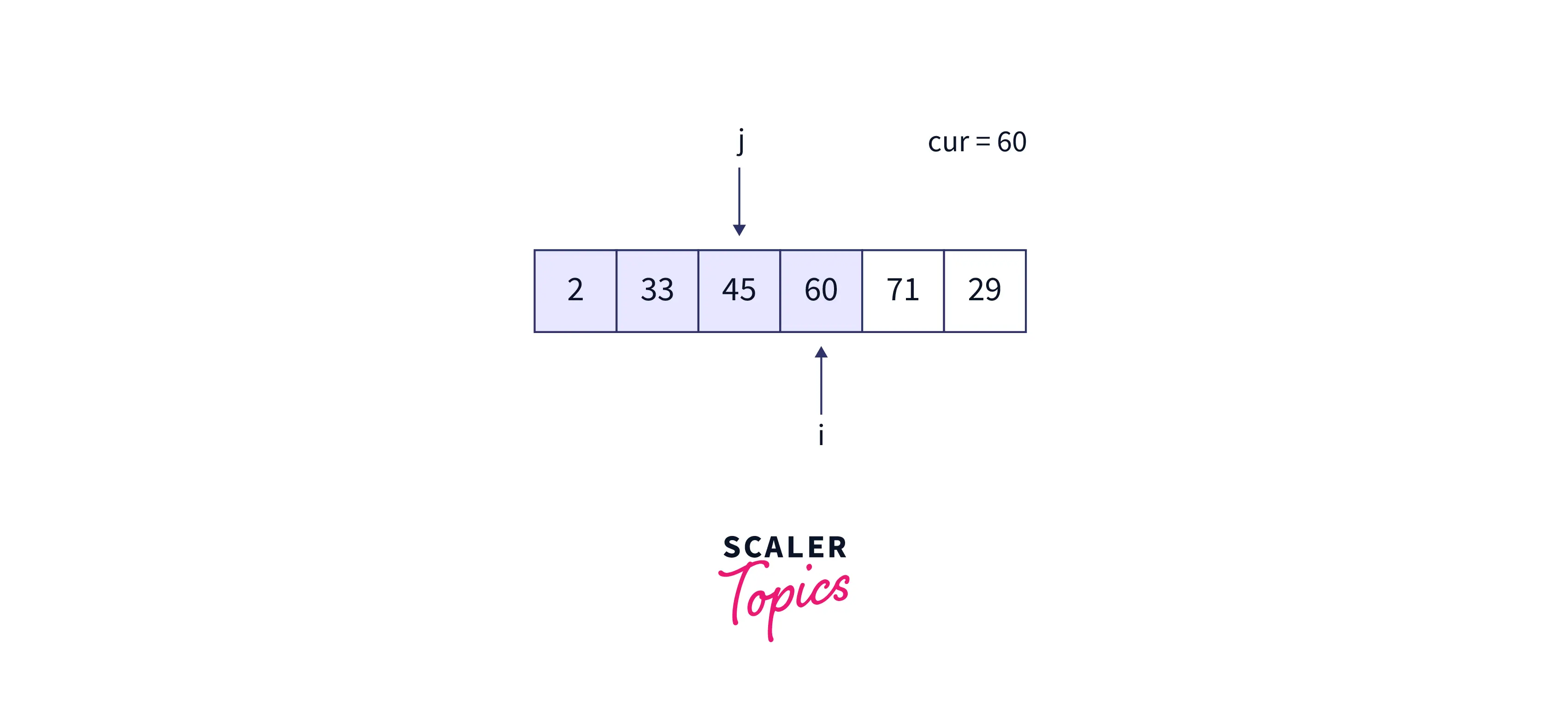
Fourth iteration:

• At the beginning of the fourth iteration,

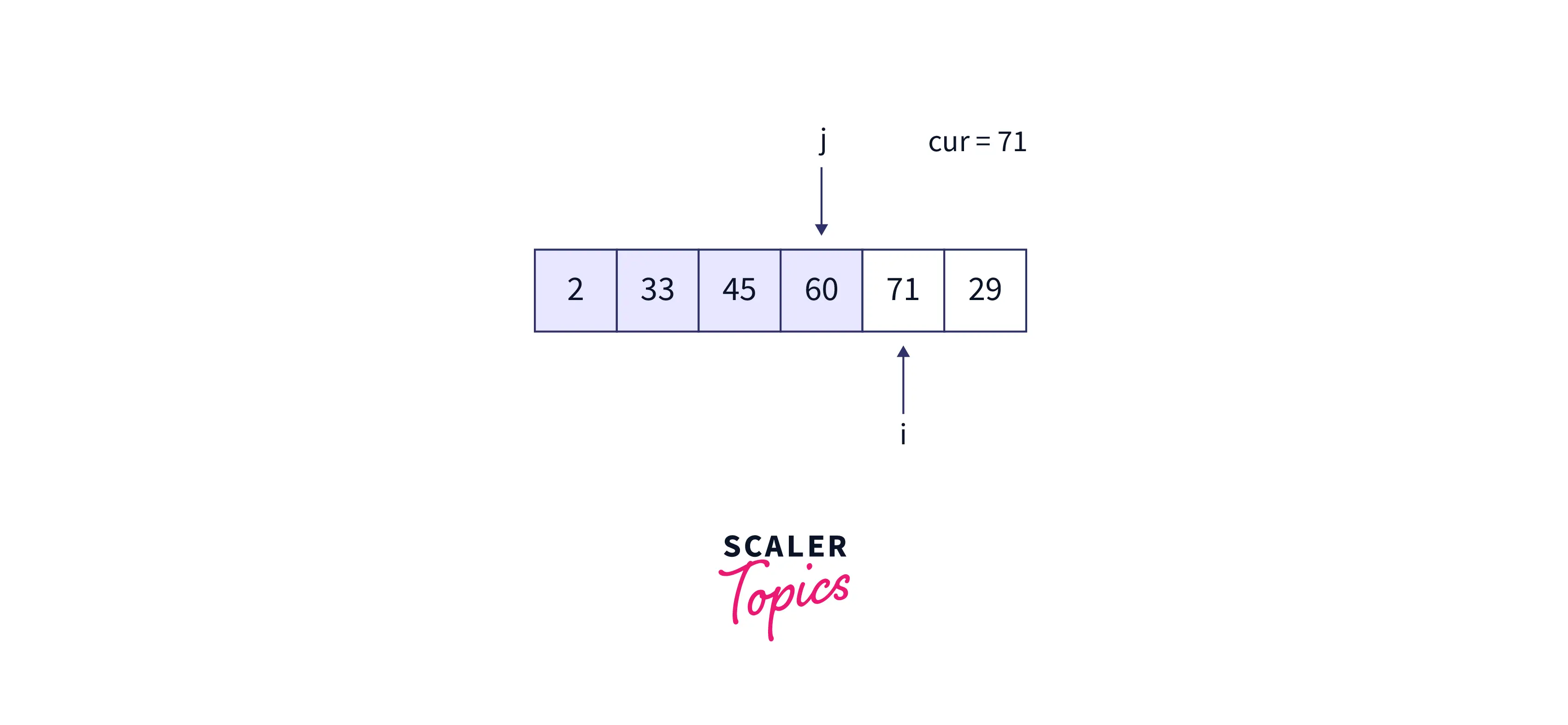
• Now, cur = 71, and j is 60, which is less than 71. Thus, again, the array is sorted so far.

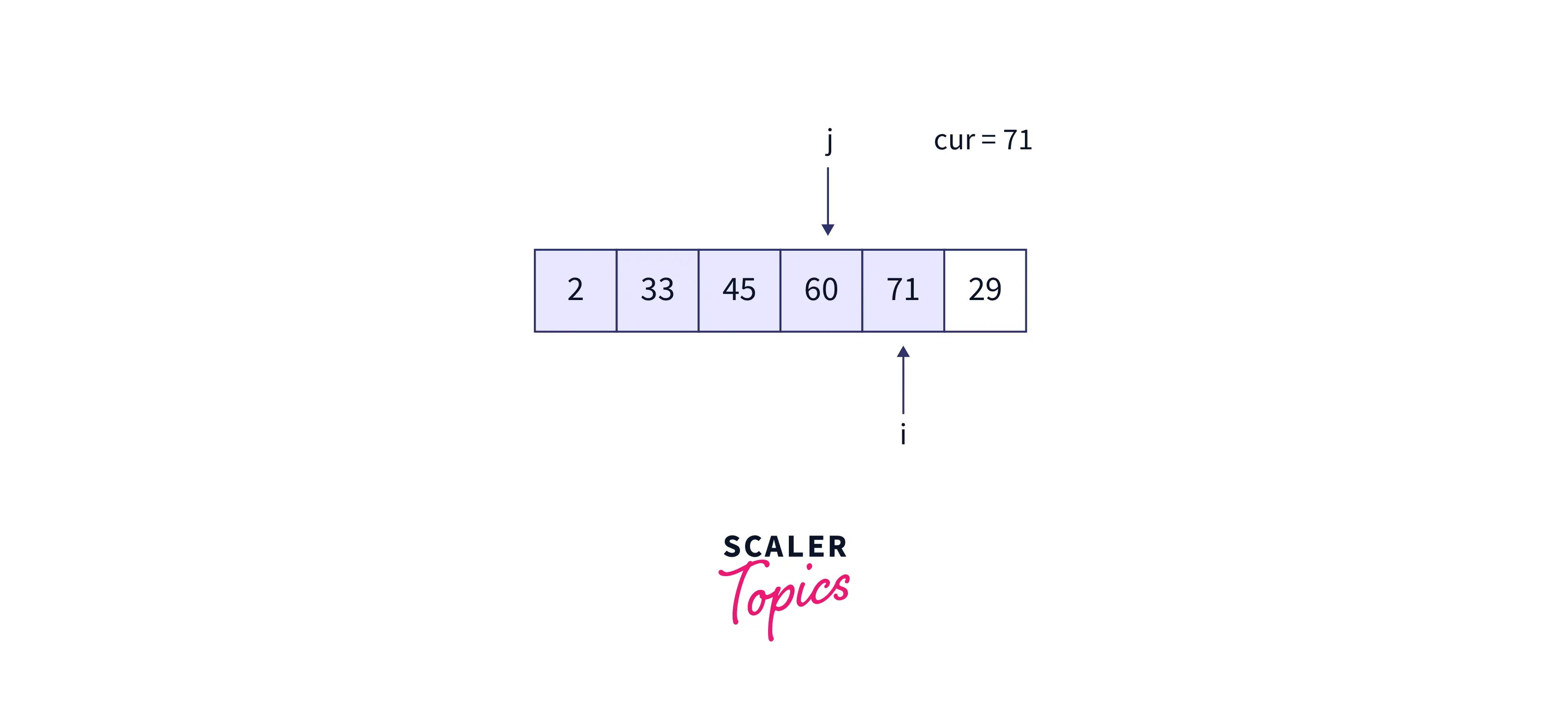
Fifth iteration:

• Array at the beginning of the fifth iteration:

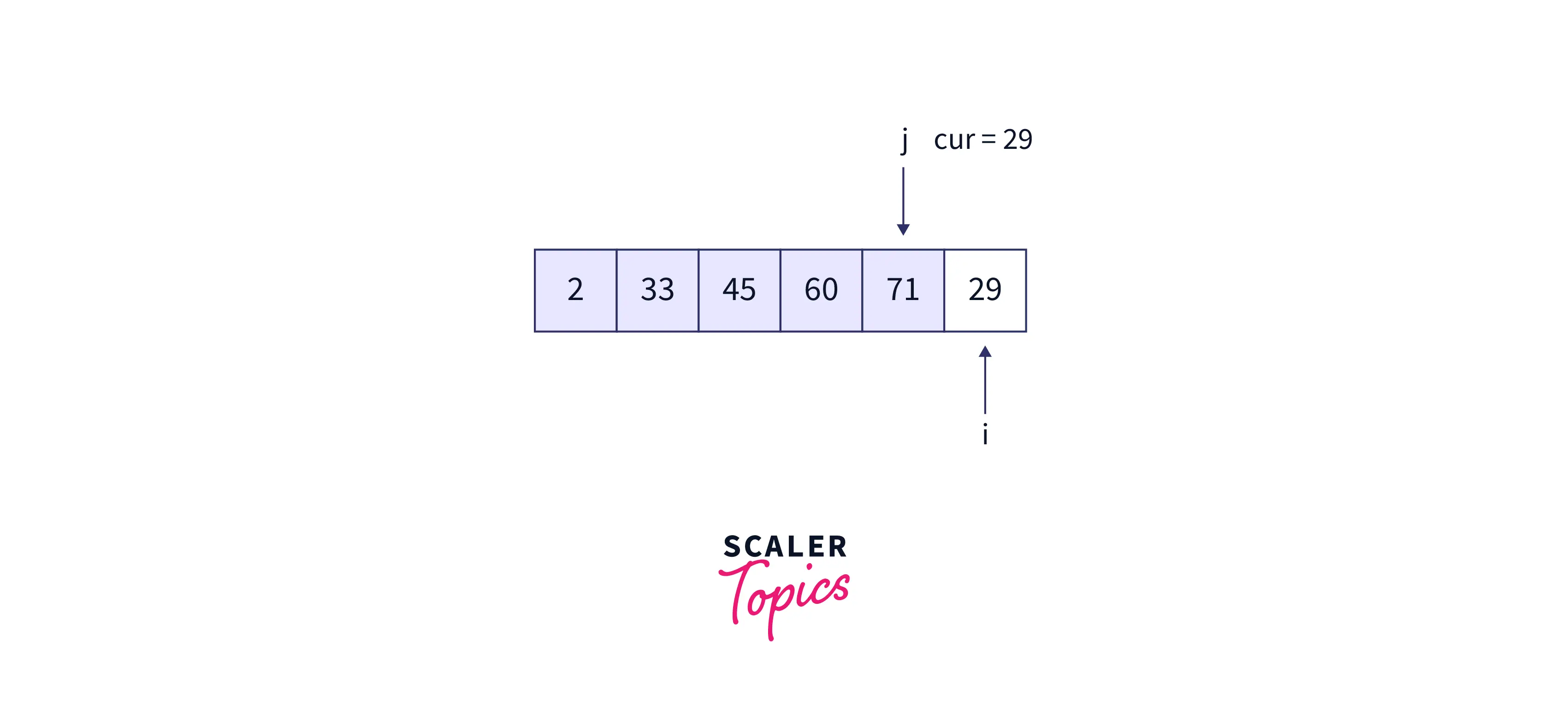
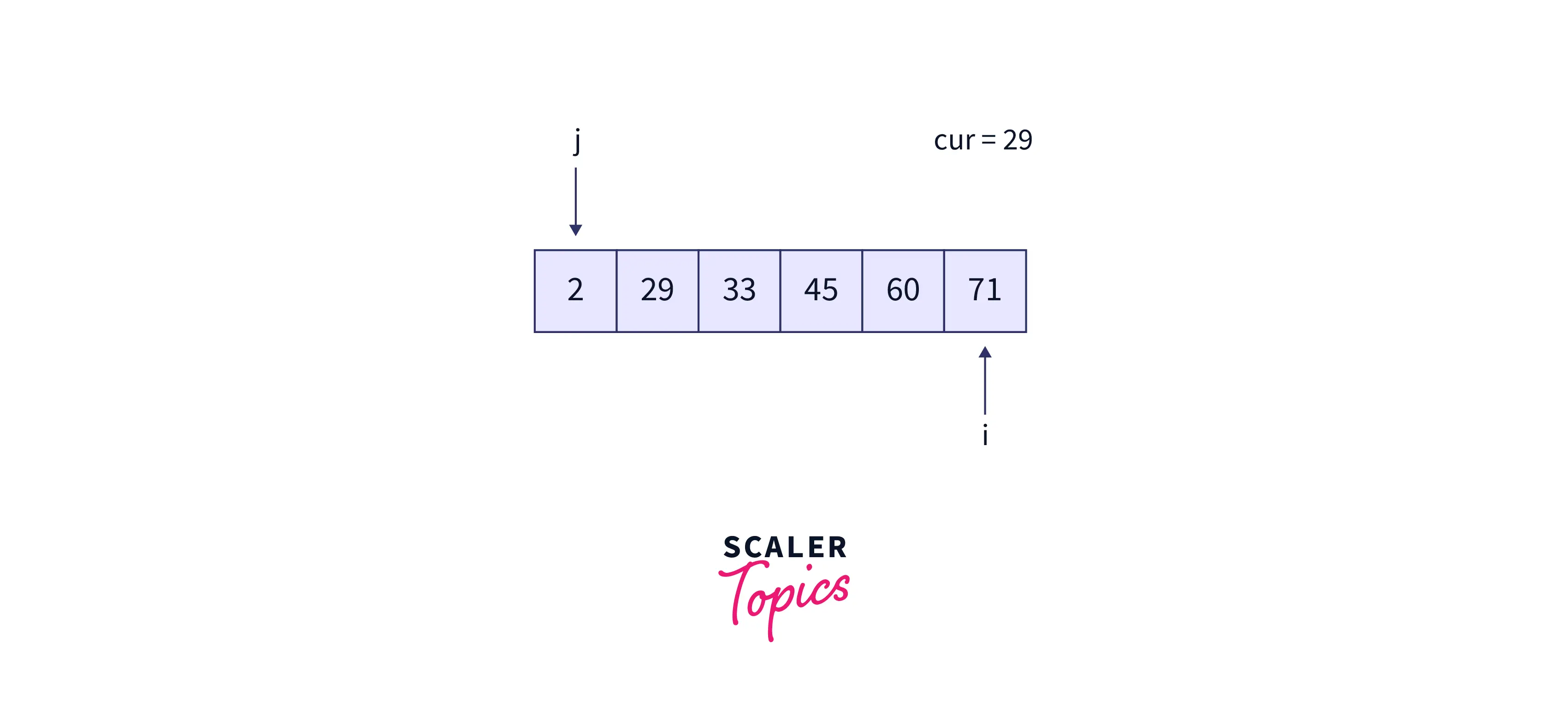
• Lastly, i points to 29 i.e. cur = 29 and j = 4 i.e. 71. Variation during the while loop in the array is as follows:

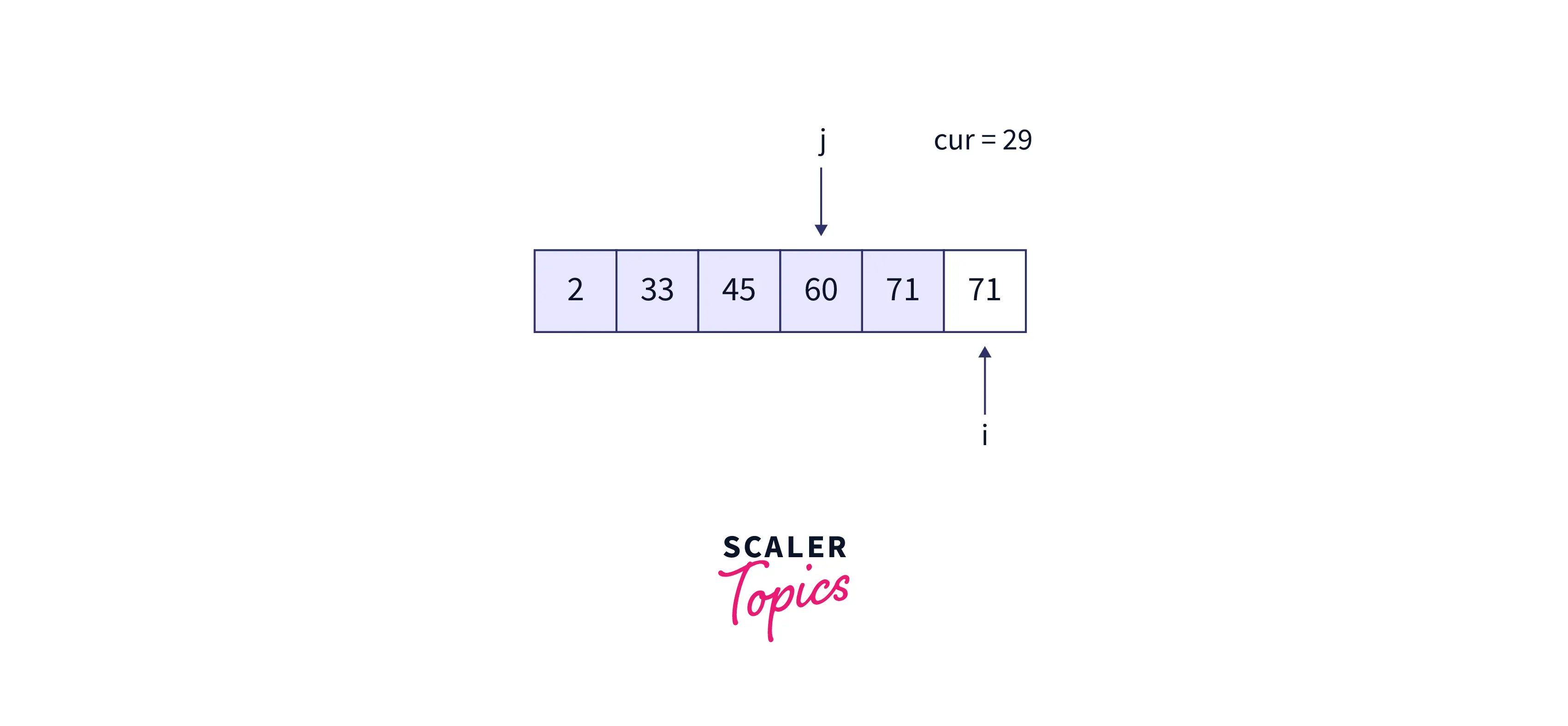
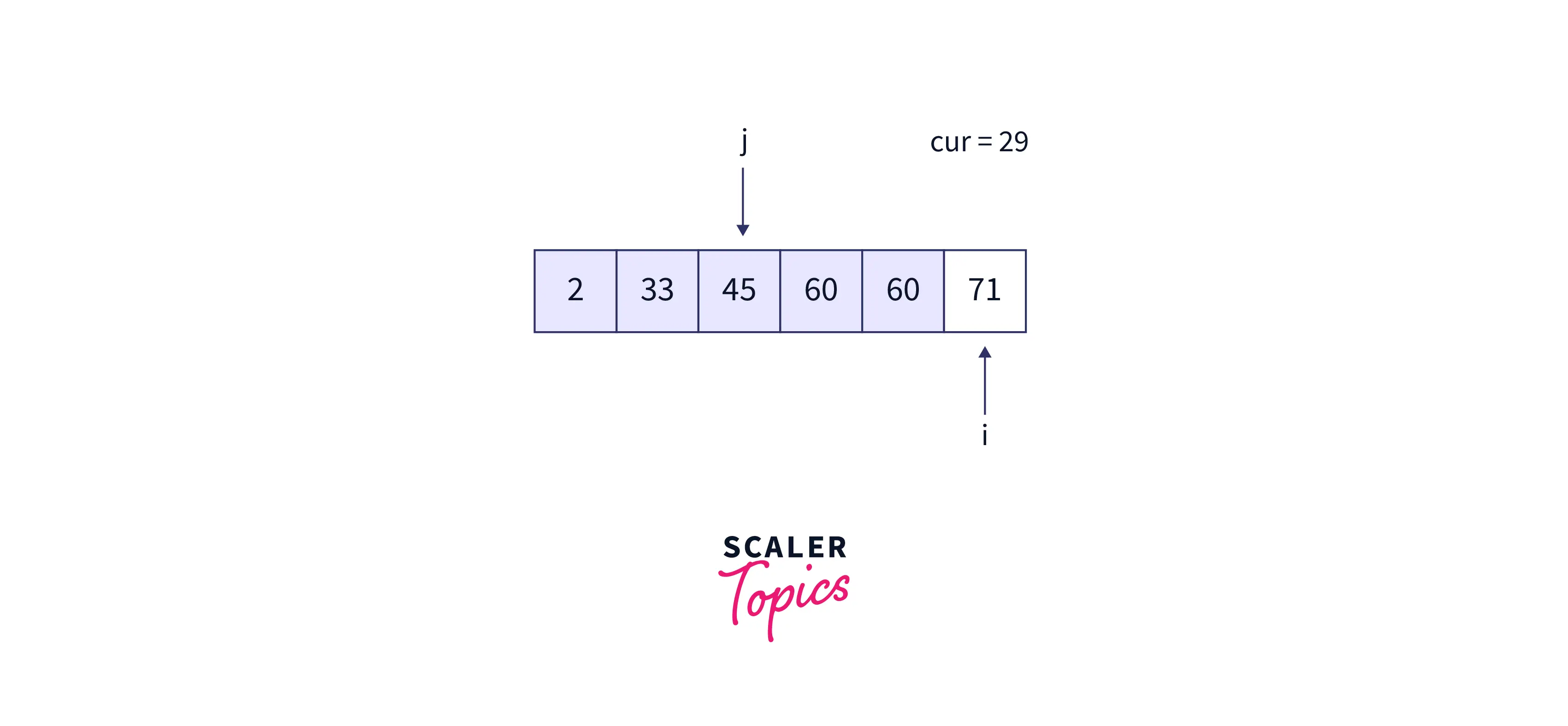
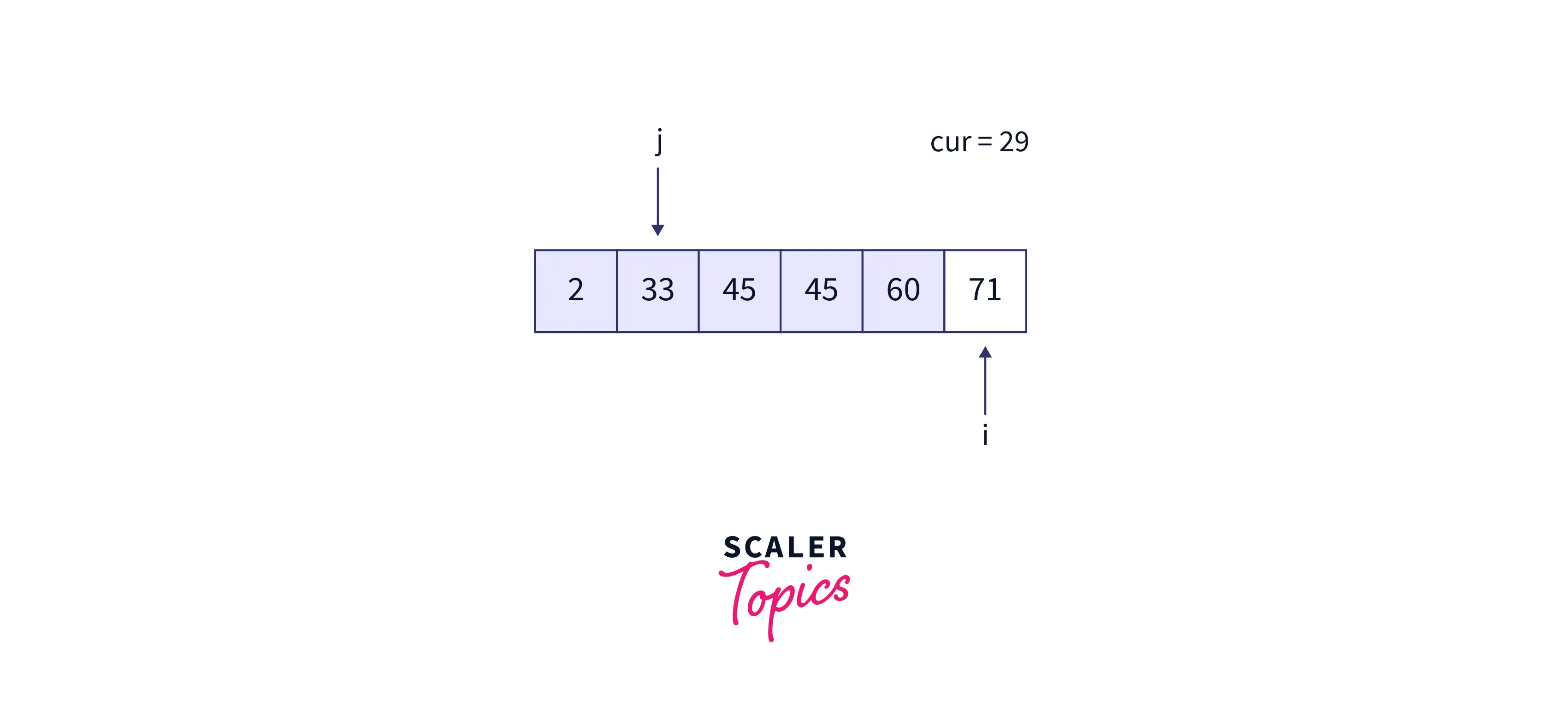
• Now, cur must be placed at position 4. The resultant array is as follows:

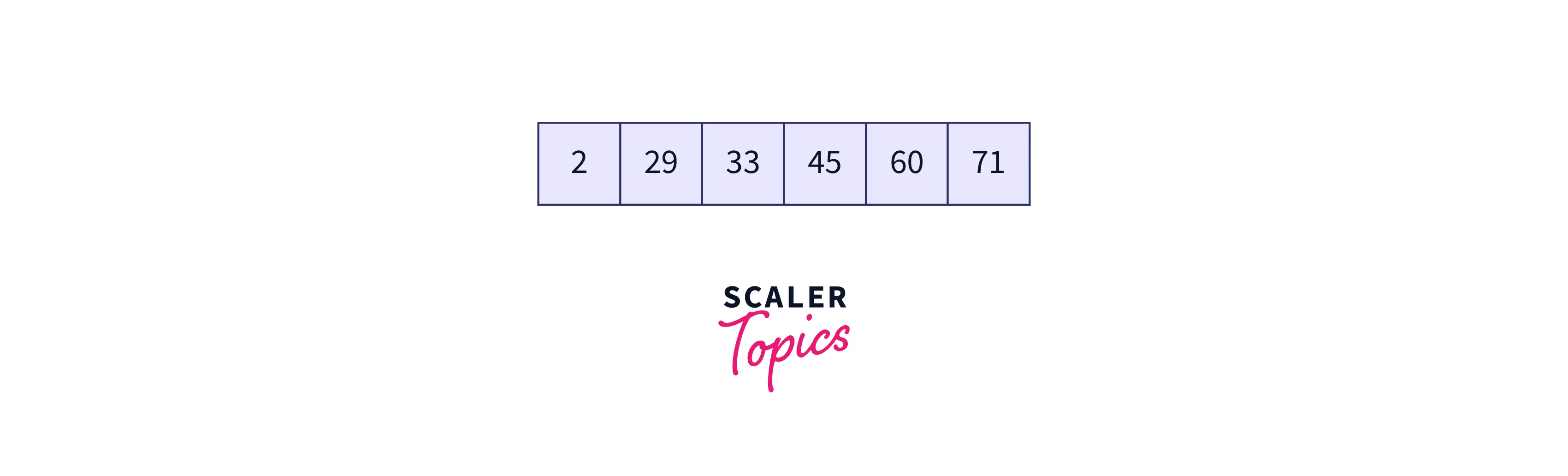
The sorted array after execution of the insertion sort is as follows:

Insertion Sort Algorithm

The steps to implement the insertion sort algorithm are described below:

1. We assume that the array is empty and that inserting one element into it will not affect the sorting order of the array. Thus, the first element is already sorted.
2. We run a loop from the second element to the last element in the array. Each iteration compares the current element with the previous elements, and its correct position is searched.
3. If the current element is greater than or equal to the previous element, then we move towards the next iteration. If the current element is smaller than the previous elements, all the elements greater than the current are shifted one position to the right, and the current element is placed at its correct position.
4. Step 3 is repeated for each element in the array.

The array is sorted now. Let us look at its pseudo code for a better understanding:

In the above code, the outer for loop visits each array element. The inner while loop moves all the elements greater than cur to the one position right. Finally, the cur is placed in the right position.

Implementation

Here, We are using an outer loop to visit all the elements of the loop and an inner while loop to search for the position of the current element and shift greater elements to one step right.

Output:

Time Complexity

• Best Case - O(n).
• Worst Case - $O(n^2)$
• Average Case - $O(n^2)$

Space Complexity

The Space complexity of the insertion sort algorithm in all the cases is O(1).

Boundary Cases of Insertion Sort in C

Boundary cases in algorithms represent scenarios where the algorithm performs at its best or worst. In the case of Insertion Sort, the best scenario arises when the input array is already sorted, while the worst scenario occurs when the array is sorted in reverse order.

In the best-case scenario, with a sorted input array, each new element in the unsorted section must only be compared once, resulting in a single pass through the array. This leads to an O(n) time complexity, where n is the array size.

Conversely, in the worst-case scenario where the array is sorted in reverse order, every new element in the unsorted section must be compared with all elements in the sorted section, necessitating the shifting of elements and resulting in a time complexity of O(n^2).

Thus, the efficiency of Insertion Sort significantly varies based on the input scenario. Understanding these boundary cases is crucial for evaluating the algorithm's performance accurately, highlighting its sensitivity to the initial order of elements in the array.

Algorithmic Paradigm of Insertion Sort in C

The insertion sort algorithm employs several algorithmic paradigms to sort arrays efficiently.

• Firstly, it adopts an iterative approach, utilizing loops to traverse the array and insert each element into its appropriate position within the sorted section.
• it applies the divide and conquer strategy by segmenting the array into sorted and unsorted portions, iteratively incorporating elements from the latter into the former until the entire array is sorted.
• Insertion sort operates in-place, necessitating no extra storage beyond the original array, which enhances its memory efficiency.
• It upholds stability, ensuring that the relative order of equivalent elements remains unchanged in the sorted output.
• Despite its effectiveness for minor to moderate arrays, its O(n^2) time complexity renders it less suitable for larger datasets.

These combined strategies enable insertion sort to organize arrays proficiently, balancing performance considerations with memory constraints and preserving the order of identical elements.