Program for Insertion Sort in Python

Insertion Sort in Python

Insertion sort is a simple sorting algorithm that divides the array into two parts, a sorted part, and an unsorted part. At each iteration, an element from the unsorted array is placed at its correct position in the sorted array.

Properties of Insertion Sort :

• In-place :
  Insertion sort is an in-place algorithm. This means that it does not require any additional space for sorting.
• Stable :
  Insertion sort is a stable sorting algorithm. Suppose we are given an array $A$, and there are two elements $A[i]$ and $A[j]$ such that $A[i] = A[j]$ and $i$ $<$ $j$. In a stable sort, the element $A[i]$ will be placed before the element $A[j]$ in the final sorted array.

Algorithm for Insertion Sort in Python

Problem Statement

Given an array $A$ containing $N$ integers. The problem is to sort the array $A$ in non-decreasing order using Insertion Sort in Python.

Example

Input :

Output :

Intuition

Insertion sort can be visualized as sorting cards in our hands. Suppose we have 5 playing cards with numbers written on them as $[10, 4, 1, 5, 4]$.

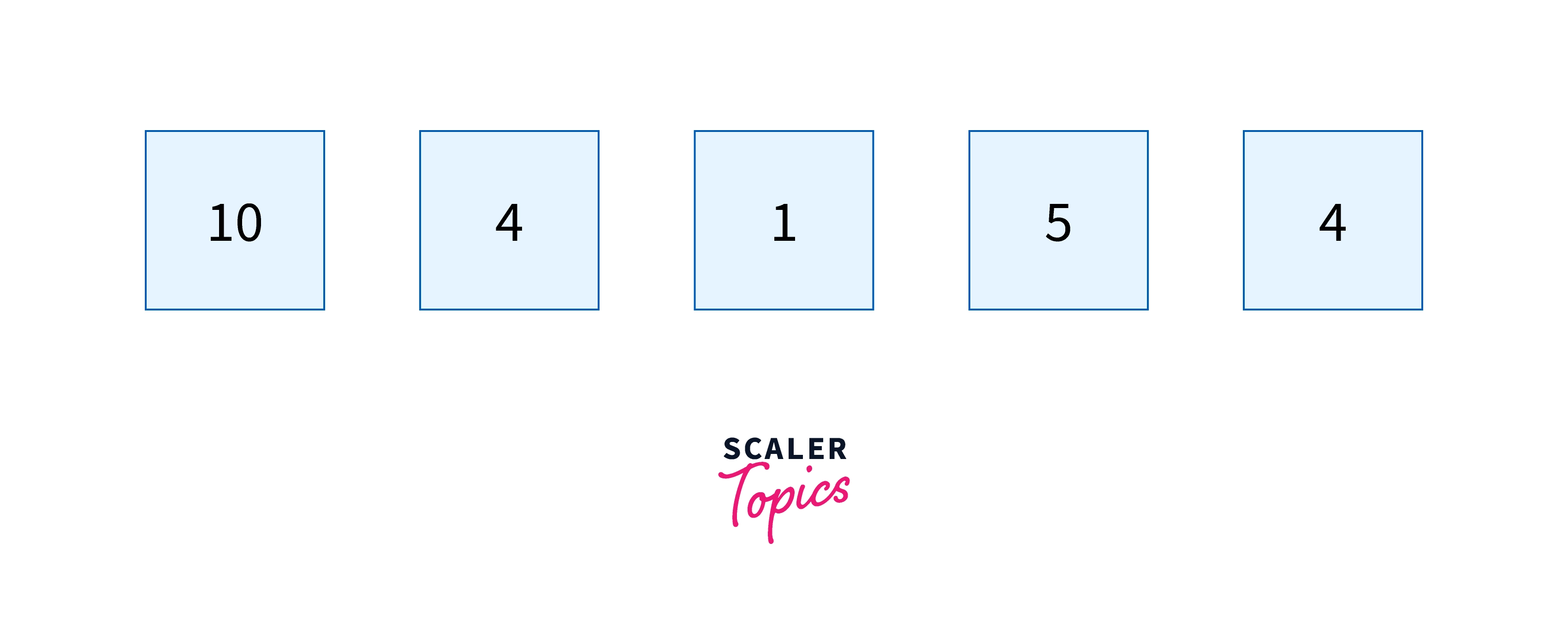
Now we assume that the first card is at its correct location and we are left with four unsorted cards $[4, 1, 5, 4]$.

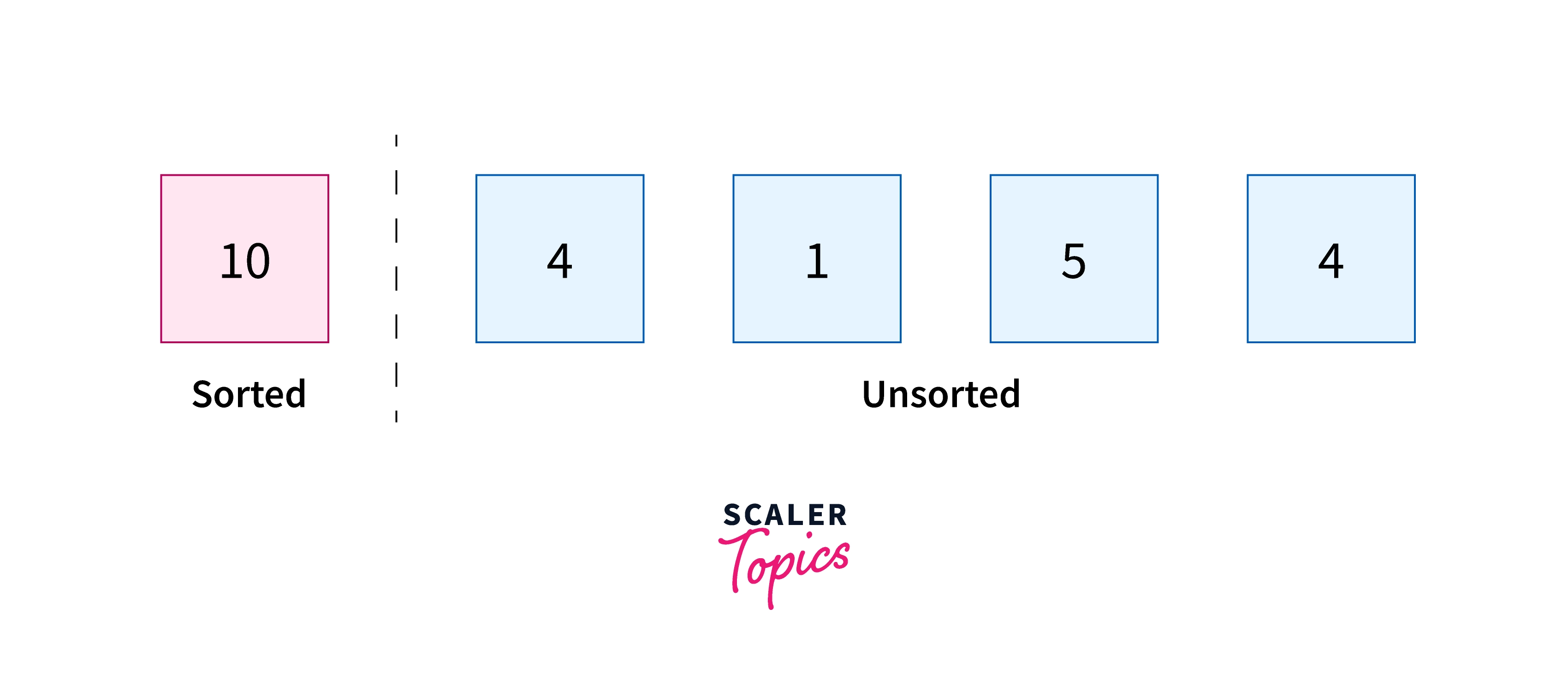
Now we pick the first unsorted card 4 and place it at its correct location, which is before the card with the number 10.

We continue the same process for each element in the unsorted part. So we pick the card numbered 1, then the card numbered 5, and so on. Each time we place it in its correct position.

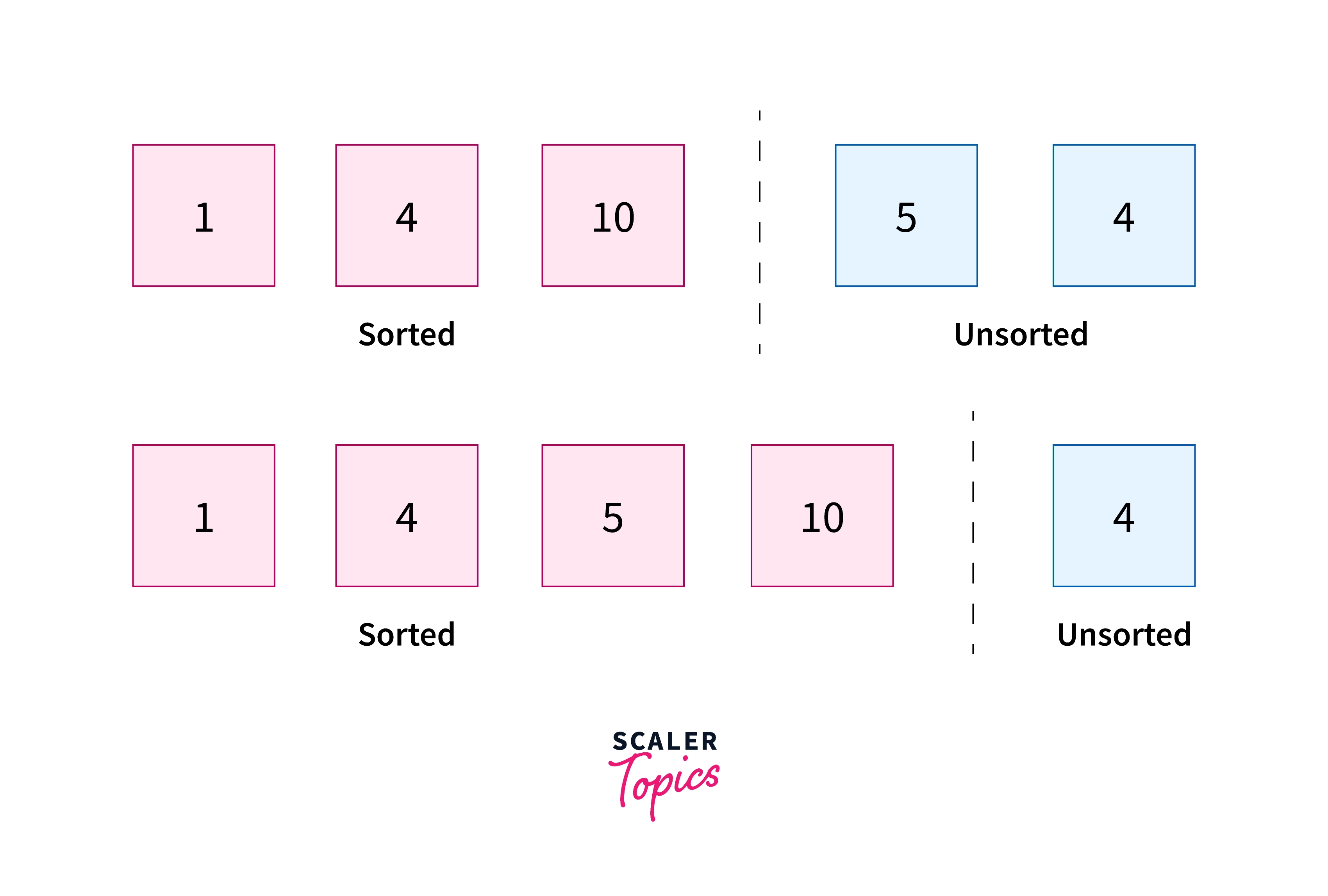
Observe that we are building the sorted sequence of cards from the front. In this way, we will end up with the sorted sequence.

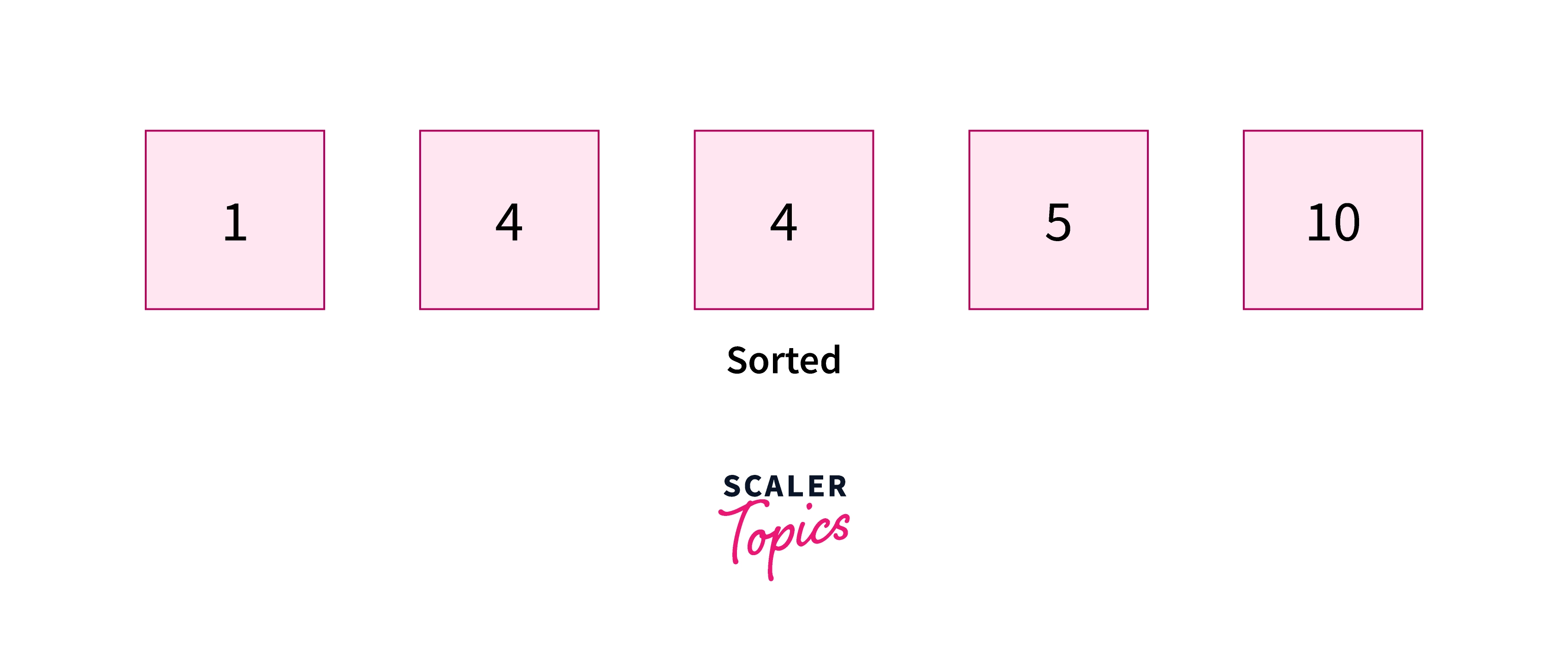
Algorithm

Suppose we are given an array A of size N.

• We consider that the first element of the array A is in its correct position.
• We iterate for all the elements $A[i]$ from $i = 1$ to $i = N - 1$. We will place the element $A[i]$ at its correct position in the prefix $A[0 ... i-1]$.
• We know that the elements from $A[0]$ to $A[i-1]$ are sorted and $A[i]$ is the first unsorted element. Let us initialize $A[i]$ to a variable $key$. So to find the correct position of $A[i]$, we compare it with all the elements $A[j]$ from $j = i-1$ to $0$.
  • Case - 1 :
    $A[j] > key$. In this case, we know the element $A[i]$ will be placed before $A[j]$ as $A[j]$ is greater, hence we shift this element $A[j]$ to $A[j + 1]$.
  • Case - 2 :
    $A[j] <= key$. In this case, we have found the correct position of $A[i]$ in the sequence. We insert the $key$ at location $j+1$.
• From the above step, we guarantee that the array from $A[0]$ to $A[i]$ is sorted and we move to the next element.

In this way, we sort array A. Let us understand this using an example.

Example :

• For $i = 1$, $key = 3$.
  • For $j = 0$, $A[j] = 5$, we can see that $A[j] > key$, so we shift $A[j]$ to $A[j + 1]$. $A = [5, 5, 2, 1, 4]$.
  • Now for $j = -1$, we break this loop at assign $A[j + 1] = key$, so $A[0] = 3$ and $A = [3, 5, 2, 1, 4]$.
• For $i = 2$, $key = 2$.
  • For $j = 1$, $A[j] = 5$ and $A[j] > key$ $\Rightarrow$ $A = [3, 5, 5, 2, 1, 4]$
  • For $j = 0$, $A[j] = 3$ and $A[j] > key$ $\Rightarrow$ $A = [3, 3, 5, 2, 1, 4]$
  • For $j = -1$, we assign $A[j + 1] = key$, so $A = [2, 3, 5, 1, 4]$
• For $i = 3$, $key = 1$.
  • For $j = 2$, $A[j] = 5$ and $A[j] > key$ $\Rightarrow$ $A = [2, 3, 5, 5, 4]$
  • For $j = 1$, $A[j] = 3$ and $A[j] > key$ $\Rightarrow$ $A = [2, 3, 3, 5, 4]$
  • For $j = 0$, $A[j] = 2$ and$A[j] > key$ $\Rightarrow$ $A = [2, 2, 3, 5, 4]$
  • For $j = -1$, we assign $A[j + 1] = key$, so $A = [1, 2, 3, 5, 4]$
• For $i = 4$ and $key = 4$.
  • For $j = 3$, $A[j] = 5$ and $A[j] > key$ $\Rightarrow$ $A = [1, 2, 3, 5, 5]$
  • For $j = 2$, $A[j] = 3$ and $A[j] < key$ so break the loop. We assign $A[j + 1] = key$ so $A = [1, 2, 3, 4, 5]$.

In this way, we perform insertion sort on the unsorted array A.

Implementation

Output :

Complexity Analysis of Insertion Sort

Time Complexity

In the implementation, we iterate for every element in the input array A and we find its correct position in the sorted prefix. To find the correct position, we again iterate over the prefix of the array A. The worst case occurs when we are given an array sorted in descending order. In this case, the second element will be compared with the 1 element, the third element will be compared with the 2 elements, and so on. So, the total number of comparisons will be equal to $(1 + 2 + 3 + … + (N-1))$ which is $O(N^2)$, so the time complexity is $O(N^2)$, where $N$ is the size of the input array.

Time Complexity : $O(N^2)$

Space Complexity

In the implementation, we use a constant number of variables, so the space complexity is $O(1)$, where N is the size of the input array.

Space Complexity : $O(1)$

Application of Python Insertion Sort

• Insertion sort can be used when the number of elements is very small. This is because insertion sort requires less memory and the runtime overhead is very small when compared to Quick sort, Bubble sort, and Merge sort. The constant factor in the overall running time is tiny in the case of insertion sort.
• If the array is partially sorted, then insertion sort can be used to sort the array quickly.
• If it is known apriori that each element, in the input array, is at most K places away from its actual position in the sorted array, then insertion sort can be useful as it gives the time complexity of $O(NK)$ where N is the number of elements in the input array.

Related Programs in Python

• Stable Sorting Algorithms
• Bubble Sort
• Selection Sort