Bitwise Operators in Java

Overview
Bitwise operators are one among those operators which perform their tasks at binary level directly on binary digits (also known as bits), the smallest form of data in a computer, or its data types. These bitwise operators are faster and an efficient way to interact with computers to make heavy computation in a linear time because it works directly with the bits rather than through a level of abstraction of software.
These bitwise operators alter data in constant time complexity and function parallelly by making it efficient on all systems, and therefore this process of altering data through bitwise operators is termed Bit Manipulation. Almost all programming languages will have to work with data abstractions(for eg, objects or variables), rather than the bits they represent. However, direct bit manipulation is required to optimize the performance of code and reduce errors in numerous scenarios.
Here are few examples of tasks that require bit manipulation or knowledge of Bitwise Operators:
- Low-level device control
- Error detection and correction algorithms
- Data compression
- Encryption algorithms
- Optimization
Introduction to Bitwise Operators in Java
The image below shows the number of steps required to perform arithmetic operations on decimal data and binary data.
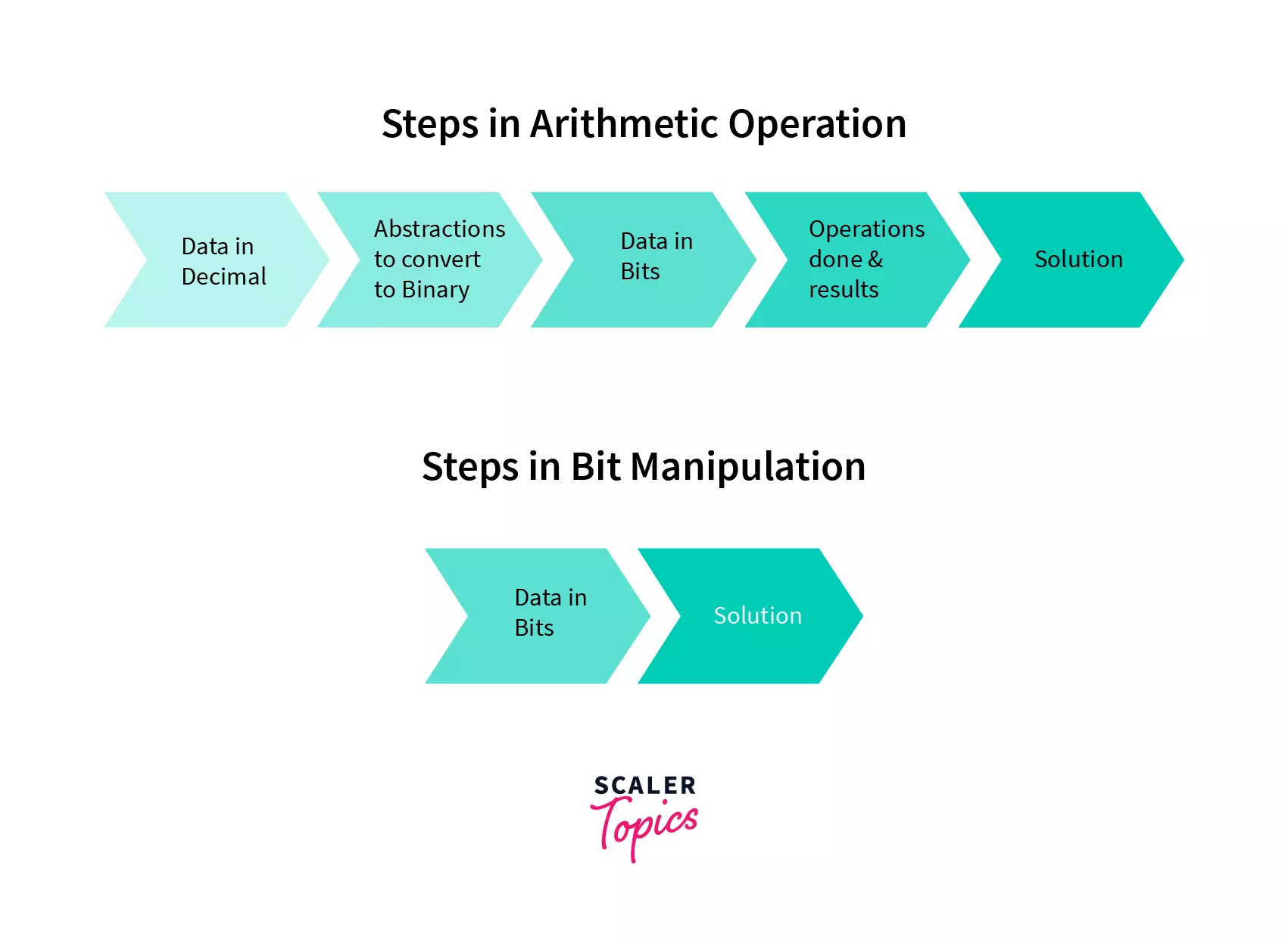
You can see how many steps are reduced with bit manipulation from normal representation.
Bit Manipulation is performed using Bitwise Operators, on each and every bit of a number individually and can be used with any data types such as int, float, short, char, etc.
Bitwise operators work on a binary equivalent of decimal numbers i.e. the operation is performed on decimal numbers and internally these operators work on individual bits bit by bit, as per the given operations:
- First, the operands are converted to their binary representation
- Next, the operator is applied to each binary number and the result is calculated
- Finally, the result is converted back to its decimal representation
Standard arithmetic operators perform operations on human-readable values (3+4), while bitwise operators manipulate the low-level data directly.
Types of Java Bitwise Operators in Java
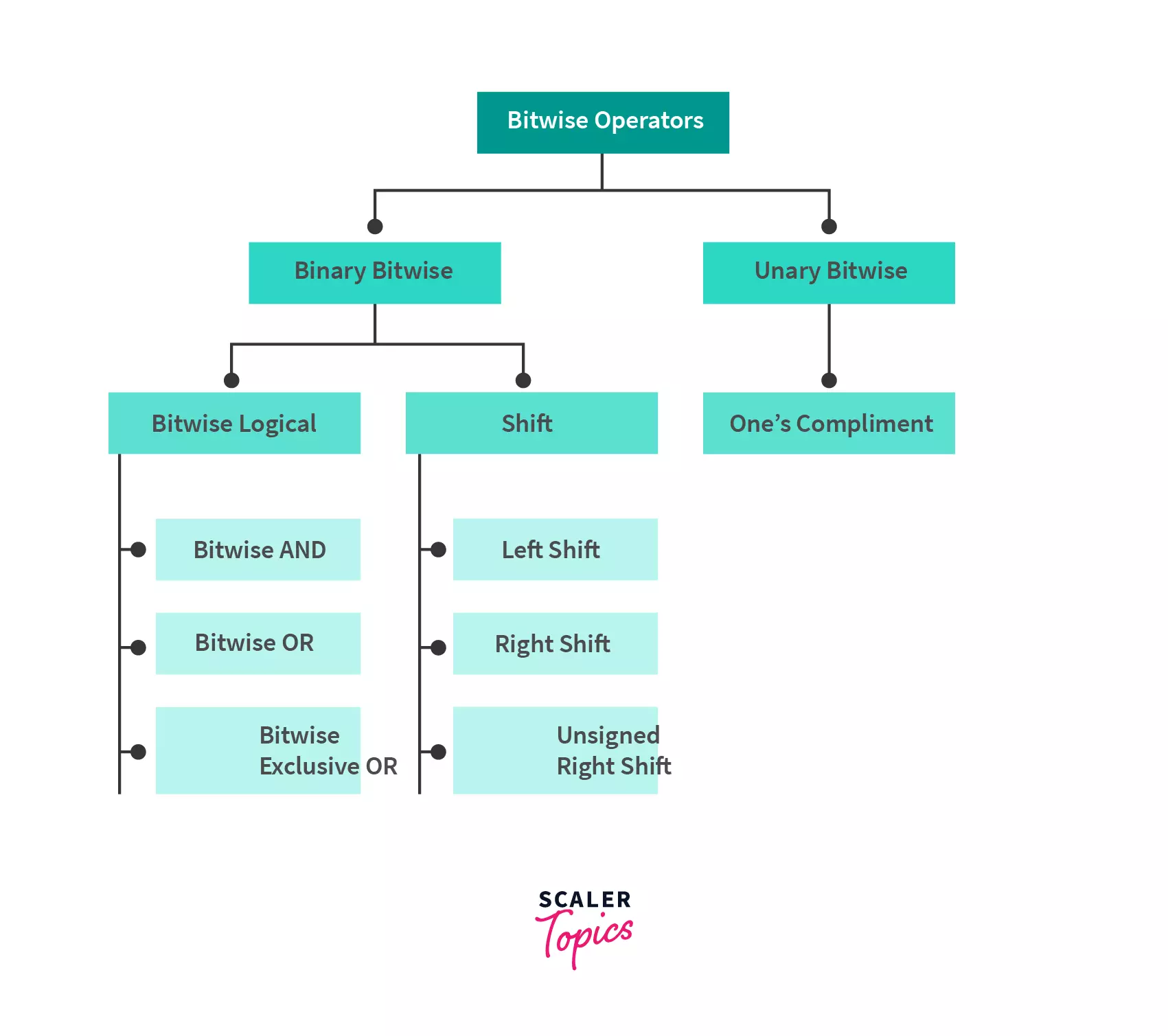
| Operators | Symbol | Uses |
|---|---|---|
| Bitwise AND | & | num1 & num2 |
| Bitwise Exclusive OR (XOR) | ^ | num1 ^ num2 |
| Bitwise Inclusive OR | \ | |
| Bitwise Complement | ~ | ~ num |
| Bitwise Left shift | << | num1 << num2 |
| Bitwise Right shift | >> | num1 >> num2 |
| Unsigned Right Shift Operator | >>> | num1>>>num2 |
Let's go through all these operators one by one.
1. Bitwise AND(&)
AND (&) is a binary operator which compares two binary operands of equal bit length (i.e. both numbers in their binary form will have same length). The operands are converted from their decimal form to binary representation. For each and every bit, the operation checks if both bits are 1 across both operands. If true, bit will be set to 1 in the answer. Else, the resulting bit is set to 0. You can understand this operation by the arithmetic multiplication. As multiplying anything by 0 ends up in 0, the AND comparison with any 0 bit will end in 0.
Its Truth Table:
Example:
We want to perform Bitwise AND Operation of 6 and 8 (6 & 8), then
-
The numbers are converted to their binary equivalent
a = 6 = 0110 (In Binary) b = 8 = 1000 (In Binary) -
Then on their binary represntation AND operation is performed.
0110 & 1000 ________ 0000 = 0 (In decimal) -
Resulting binary number is converted to decimal and printed to user as result.
2. Bitwise OR(|)
The OR (|) operator is a binary operator that takes two equal-length operands but compares them in the following way:
- If either corresponding bit is 1, the answer is 1.
- Otherwise, the answer will be 0.
In other words, Bitwise OR of two bits returns ‘1’ if at least one of the bits is 1. You can get idea from arithmetic addition operation, adding anything with 0 results the same.
- If two input bits are 0, the output is 0.
- In all other cases, it is 1.
Its Truth Table:
Example:
We want to perform Bitwise OR Operation of 6 and 8 (6 | 8), then
-
The numbers are converted to their binary equivalent
a = 6 = 0110 (In Binary) b = 8 = 1000 (In Binary) -
Then on their binary represntation OR operation is performed.
0110 | 1000 ________ 1110 = 14 (In decimal) -
Resulting binary number is converted to decimal and printed to user as result.
3. Bit Shift (>>, <<,>>>)
A bit shift is a Bitwise operation where the order of a series of bits is moved to efficiently perform a mathematical operation. A bit shift, shifts each digit in a number’s binary representation left or right by as many spaces as specified by the second operand. These operators can be applied to integral types such as int, long, short, byte, or char.
There are three types of shift:
a. Left shift: << is the left shift operator and meets both logical and arithmetic shifts’ needs.
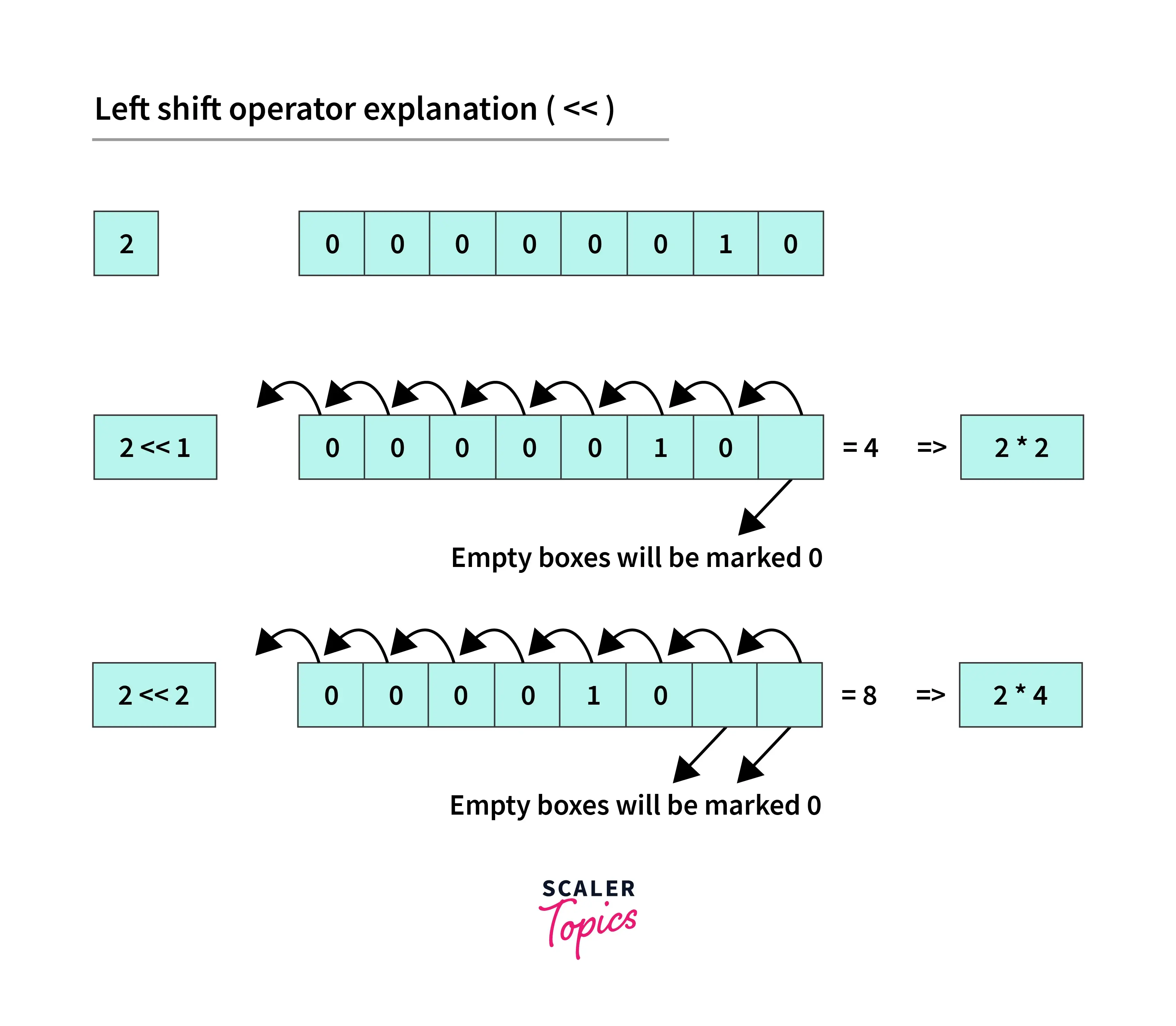
Example:
b. Arithmetic/signed right shift: >> is the arithmetic (or signed) right shift operator.
Example:
c. Logical/unsigned right shift: >>> is the logical (or unsigned) right shift operator. It performs same operation as right shift operator but its sign is not preserved in the operation.
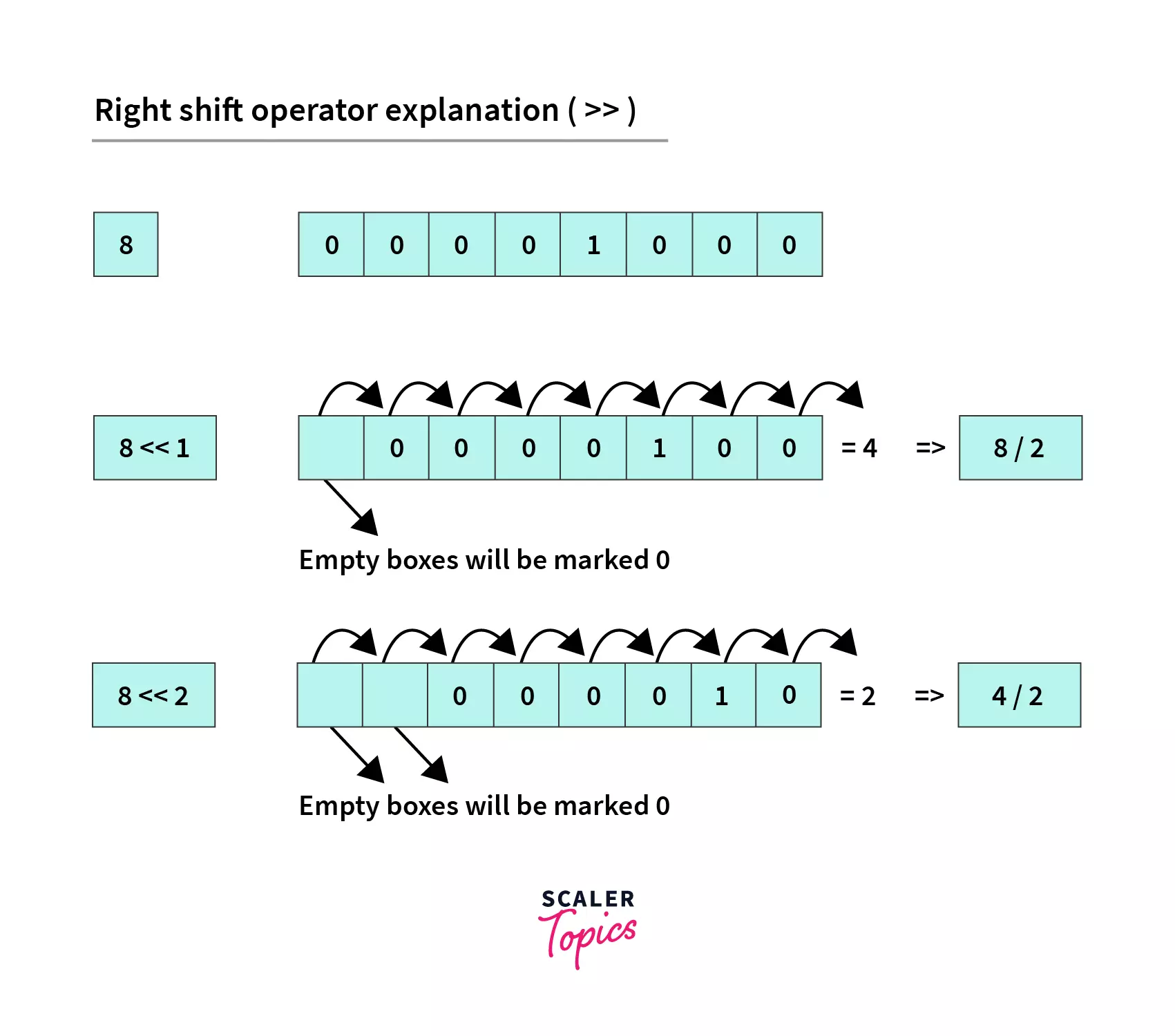
Example:
In Java, all integer data types are signed and << and >> are solely arithmetic shifts.
4. Bitwise Complement (~)
The Bitwise Not or Complement operator simply means the negation of each bit of the input value. It takes only one integer. All samples of 0 become 1, and all samples of 1 become 0. In other words, NOT invert each input bit. This inverted cycle is called the 1’s complement of a bit series.
This makes the number negative as any bit sequence that starts with 1 is negative, as here N = ~N produce results -(N+1) always. Because system store data in form of 2's complement which means it stores ~N like this.
Example:
We want to perform Bitwise Complement of 6 (~6), then
-
Representing the number in binary format a = 6 => 0110 (In Binary)
-
Now we have to find ~6(means 1's compliment of 6) 0000 0110 => 1111 1001 (flip each 1's to 0 and vice versa) So, ~6 = 1111 1001, Here MSB(Most significant Bit) is 1(means negative value). Then, in memory it will be represented as 2's compliment (To find 2's compliment first we have to find 1's compliment and then add 1 to it.)
-
Finding 2's compliment of ~6 i.e 1111 1001
- Converting back to decimal format. 0000 0111 => 7
In step2: we have seen that the number is negative number so the final answer would be -7
So, ~6 === -7 (result of bitwise complement)
NOT is useful for reversing unsigned numbers to the mirrored value on the opposite side of their midpoint.
5. Bitwise XOR (^)
The bitwise XOR operation (^), is a binary operator that takes two input statments and compares it each corresponding bit. If the bits are opposite, the solution has a 1 in that bit position and if they are matched, a 0 is returned.
Example:
We want to perform Bitwise XOR Operation of 6 and 8 (6 ^ 8), then
-
The numbers are converted to their binary equivalent
a = 6 = 0110 (In Binary) b = 8 = 1000 (In Binary) -
Then on their binary represntation XOR operation is performed.
0110 ^ 1000 ________ 1110 = 14 (In decimal) -
Resulting binary number is converted to decimal and printed to user as result.
- XOR is used to flip selected single bits in a register or replace bit patterns that show Boolean states.
- It is widely used in cryptography as well as in producing parity bits for checking error and fault tolerance.
Difference between Logical and Bitwise Operators
There are a couple of differences between the bitwise and logical operators.
- First bitwise operators in java work on binary representations of integer values (long, int, short, char, and byte) and return an integer, whereas logical operators work on boolean expressions and return boolean values (either true or false).
- Also, logical operators always assess the first boolean expression and, depending on its result and the operator used, may or may not assess the second. On the other hand, bitwise operators always assess and evaluate both operands.
- At last, logical operators are used in making solution based on different conditions, whereas bitwise operators work on bits and use bit manipulation for result.
- Bitwise AND operator is represented as & and a logical AND operator is represented as &&. Similarly, the Bitwise OR operator is represented as | and the logical OR operator is represented as ||.
Use Cases and Benefits of Bitwise Operators in Java
- You will have situations where you would like to set/clear/toggle just one specific bit of a register without operating on the whole register. Using bitwise operators you can do a read and perform an OR/AND/XOR operation with the suitable mask to modify only the desired bit position.
- Usually bitwise operations are faster than doing multiply/divide. So if you wish to multiply a variable x by say 9, you'll do (x<<3 + x) which might be some cycles faster than x*9.
- Similarly if you wish to use an array as a circular queue, it'd be faster(and more elegant) to handle wrap around checks with bit wise operations. (your array size should be a power of 2). Example:
- Also if you want a error flag in a program to hold multiple errors codes together for multiple scenarios, each bit can hold a separate value. You can AND it with each individual error code as a check. One such use case is Unix error codes.
- Also a n-bit bitmap can be a compact data structure. If you want to allocate a resource pool of size n, we can use a n-bits to represent the current status.
- In Compression & Encryption where both of these are heavily dependent on bitwise algorithms. Look at the deflate algorithm for an example - everything is in bits, not bytes. For example:- Huffman Coding (for compression) and Data Encryption Standard (for encryption)
Tricks in Bitwise Operators in Java
Always use Bitwise operators instead of arithmetic operators wherever we can use them because the operation through Bitwise operators in java is much faster than the arithmetic operators. This is because the Bitwise operators directly work on bits while others first convert the variables or constants into bits then make operations on them then again convert them back into decimal values and that’s why it takes time.
Let’s look at some examples for Bitwise operations in Java:
1. Check for Even and Odd Numbers
There are multiple logic to check if given number is even or not using bitwise AND, OR, and XOR operators. Let's suppose we have a number n, then using:
- If the result of AND bitwise operation between n and 1 as n&1 is equal to 0, the number is even, otherwise odd.
- If result of XOR bitwise operation between n and 1 as n^1 increments n by 1 it is even, otherwise odd.
- If the result of OR bitwise operation with n as n|1 increments the value of n by 1, it is even, otherwise odd.
Code:
Output for Above Code:
Explanation:
- Let's take a number, num = 34 (representing in bits, 100010). Now, 100010 & 1 = 000000 = 0, hence it is even.
- Again let num = 11 (representing in bits, 1011). Now, 1011 ^ 1 = 1010 which is 10 in decimal. As the value of the number has decreased, num is odd.
- Finally let num = 13 (representing in bits, 1101). Now, 1101 | 1 = 1101 whic is 13 in decimal. As the value of the number is unchanged, hence odd number.
Time Complexity for all three bitwise operation is O(1).
2. Change Character to Uppercase or Lowercase
Similar to the previous example, in this also we will use bitwise operators to convert to Uppercase or Lowercase
Now look at this code:
Output:
Explanation:
- The ASCII code of letter A is 65 (in bits, 1000001) and 32 in bits is 100000.
- Now, 'A' & 32 = 65 & 32 = (1000001) | (100000) = 1100001 (97) and ASCII code for a is also 97.
- So after casting 97 into char it gives ‘a’. Similarly for other uppercase characters, this operation gives the corresponding lowercase character.
Some Practice Problems on Bitwise Operators
1. Swap two numbers using Bitwise Operators
This is a simple swapping problem in which we have to swap two numbers using the XOR operator.
Below code makes XOR operation on the given numbers to swap them:
Output:
Explanation:
- Here, a = 33 (representing in bits, 100001) and, b = 79 (representing in bits, 1001111).
- Now, first a = a ^ b = 100001 ^ 1001111 = 1101110, then b = a ^ b = 1101110 ^ 1001111 = 100001 and then last step, again a = a ^ b = 1101110 ^ 100001 = 1001111.
- This works due to the following properties of XOR operation:
Now you can see that both the numbers are swapped i.e., a becomes 1001111 (79) and b becomes 100001 (33).
2. Number of Set Bits in an Integer
In this problem, we will use AND(&) and right-shift(>>) operators to find out the number of set bits in a number. Whenever we calculate the binary representation of an integer value then it is formed as the combination of 0’s and 1’s. So, the digit 1 is known as set bit and this example counts the number of 1's in the binary representation of a decimal number.
Now consider below code:
Output:
Explanation:
- In this problem, we are just looping on the number, till it becomes 0.
- Inside the loop, it is checked the rightmost bit is 1 or not (using AND operation) and then remove the rightmost bit using the right-shift operator.
- We are removing the rightmost bit, so that we can access each bit of the given number one by one.
Let’s understand this step by step
Consider, a = 79 (1001111).
Step1: Check rightmost bit is 1 or not, as 1001111 & 1 is equal to 1 then increase setBits count by 1
Step2: Then, remove the rightmost bit of a, now a becomes 100111
Step3: Continue looping on Step1 and Step2 until a becomes equal to 0.
3. Check the ith bit of a number is 1 or 0
In this problem, we will find out that the ith bit (starting from 0th bit from the end) of any number is 0 or 1 using AND(&) and left-shift(<<) bitwise operators.
Now consider below code:
Output:
Explanation:
- The above technique used is called Bit-Masking. In this approach, we first create a mask (based on the problem given) and make a bitwise operation of the mask with the given number.
- In this problem the mask will be 1 << i which basically creates a set bit at ith index keeping the bit 0 at all other indices.
- After performing the AND operation if the result is equal to 0 then the ith bit from the end is 0 otherwise 1.
Conclusion
- There are various bitwise operators such as:
- AND(&)
- OR(|)
- Complement (~)
- Bit Shift (>>,<<,>>>) and
- XOR (^)
- Bitwise operators are faster than standard arithmetic operators which operate on decimal numbers. It is because it directly operates on the bits and no conversion computations are performed in its case.
- Logical and Bitwise operations are two different types of operations. The first one operates on boolean data types whereas the latter operates on bits.
- AND bitwise operator returns 1 if and only if both bits are set.
- OR bitwise operator returns 1 if at least one of the operand bits is set.
- XOR bitwise operator returns 1 if the operand bits are opposite in value.
- We can create masks to target a particular bit in a binary operation.
- To determine whether a number is odd or even, we can use bitwise operators such as AND, OR or XOR operators.
