Job Sequencing with Deadlines
Overview
In the Job Sequencing with Deadlines problem, the objective is to find a sequence or the order of the jobs, which is completed within their deadlines and gives maximum profit, given the condition that we are using a single processor OS (operating system) which is capable of performing one job at a time.
What is Job Sequencing with Deadlines in OS?
Let's understand the problem of job sequencing with the help of a similar real-life example, suppose you are a content writer and have 4 articles to write. Each article takes a different amount of time to complete and has different payments. You want to earn the maximum amount by writing the articles.
So which article will you write first? You have two options:
-
Article with maximum payment - In this case, the article can take a longer duration to complete but by writing this article, you may miss some other articles which can be completed in a shorter interval of time, and it can be unprofitable to you if the sum of the payments from the missed articles is greater than the payment of this single article which you are doing.
-
The article which takes less time: In this case, it may happen that you have written multiple articles in the given time but there could be the possibility that if you would have chosen the article with maximum payment, you could have earned more, even by writing a single article.
We will see how we can solve such problems in real life by understanding the job sequencing problem.
The job sequencing problem states that you have a single processor operating system and a set of jobs that have to be completed with given deadline constraints. Your objective is to maximize the profit, given the condition that only one job can be completed at a given time.
Job Sequencing with Deadlines Algorithm
The simple and brute-force solution for this problem is to generate all the sequences of the given set of jobs and find the most optimal sequence that maximizes the profit.
Suppose, if there are n number of jobs, then to find all the sequences of jobs we need to calculate all the possible subsets and a total of subsets will be created. Thus, the time complexity of this solution would be .
To optimize this algorithm, we can make use of a greedy approach that produces an optimal result, which works by selecting the best and the most profitable option available at the moment.
Here are the greedy algorithm steps to perform the job sequencing algorithm
- Sort the jobs in decreasing order of their profit.
- Find the highest deadline among all deadlines and draw a Gantt chart up to that deadline.
- Now, we need to assign time slots to individual job ids.
- Now pick each job one by one and check if the maximum possible time slot for the job, i.e., its deadline, is assigned to another job or not. If it is not filled yet, assign the slot to the current job id.
- Otherwise, search for any empty time slot less than the deadline of the current job. If such a slot is found, assign it to the current job id and move to the next job id.
- Continue this process until all the feasible jobs are allocated to their time slot.
- In the end, we can calculate the profit for all the allocated feasible jobs.
Implementation of Job Sequencing with Deadlines:
Job Sequencing with deadlines problems can have many solutions. An optimal solution to this problem should give the maximum profit. And that's why we can use the Greedy approach here. The greedy solution described below always gives the optimal solution to this problem.
In this code, each job has three components its unique id, profit, and the deadline associated with that job.
First, we sorted the jobs in descending order of profit so that the job with the highest profit can be selected first. Then initialize all slots as empty by marking the elements in the slot array as false, then select jobs one by one and see if their deadlines are assigned to another job or not. If it is not occupied yet, then we can assign a slot to the current job ID.
But, if the slot is filled, then, search for any empty time slot less than the deadline of the current job. If such a slot is found, then assign that slot to the current job id and move to the next job id. If in case no empty slot is found, that means that we can't assign any time slot to that job and we will skip that job id and the next job. This process will continue until all the feasible jobs are allocated to their time slots.
The time complexity for the above job scheduling algorithm is in the worst case when we will look for all the slots in the Gantt chart for a given job id and on average, n jobs search n/2 slots. So, this would also take time approximately time in the best and average cases ace complexity is as extra space is used in the above implementation.
Problem Statement:
In the table below, jobs with their profits and deadlines are given. What would be the optimal sequencing of jobs which will give maximum profit?
| Jobs | Deadlines | Profits |
|---|---|---|
| Job 1 | 5 | 200 |
| Job 2 | 3 | 180 |
| Job 3 | 3 | 190 |
| Job 4 | 2 | 300 |
| Job 5 | 4 | 120 |
| Job 6 | 2 | 100 |
Solution:
- Step 1:
Sort the jobs in decreasing order of their profit.
| Jobs | Deadlines | Profits |
|---|---|---|
| Job 4 | 2 | 300 |
| Job 1 | 5 | 200 |
| Job 3 | 3 | 190 |
| Job 2 | 3 | 180 |
| Job 5 | 4 | 120 |
| Job 6 | 2 | 100 |
As you can see from the table above, the jobs have been sorted in descending order of their profit.
- Step 2:
Here we can see that value of the maximum deadline is 5.
Its Gantt chart will be :
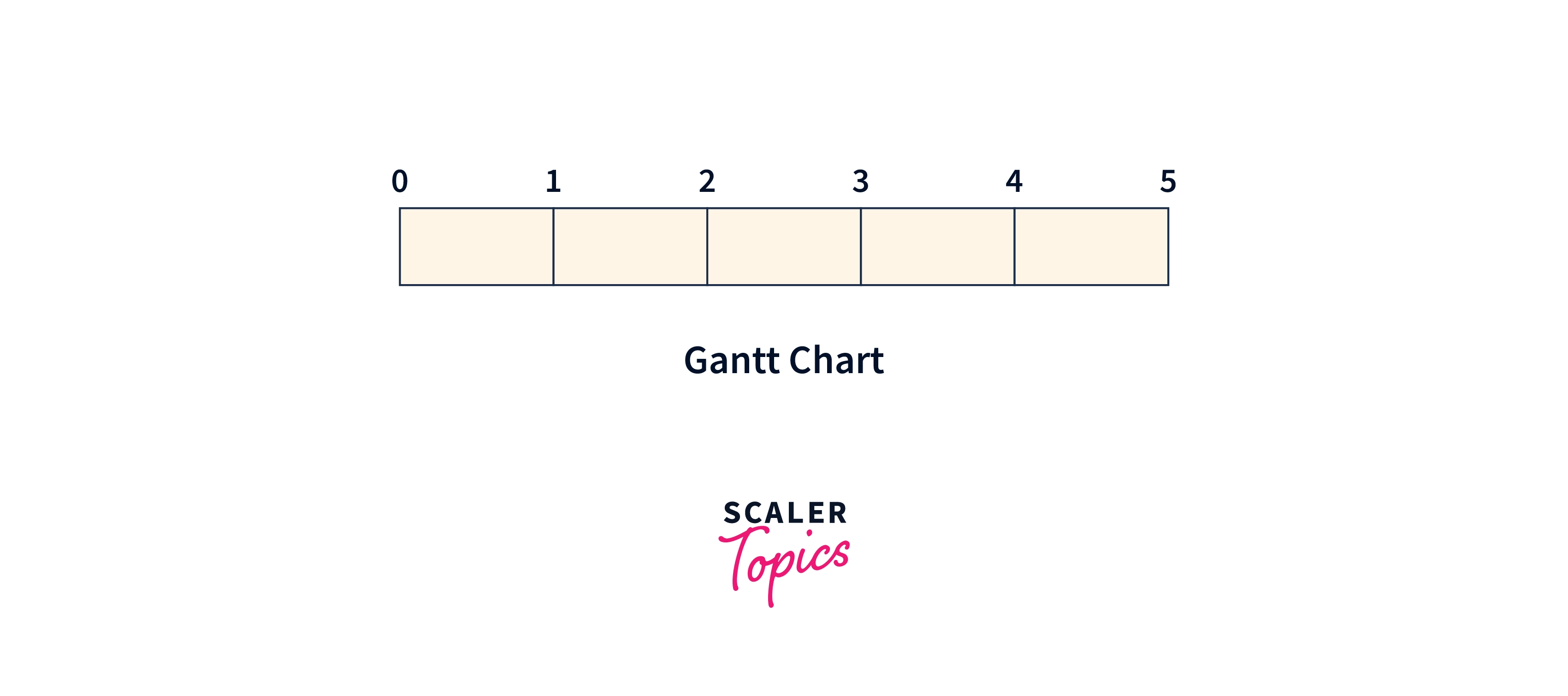
- Step 3
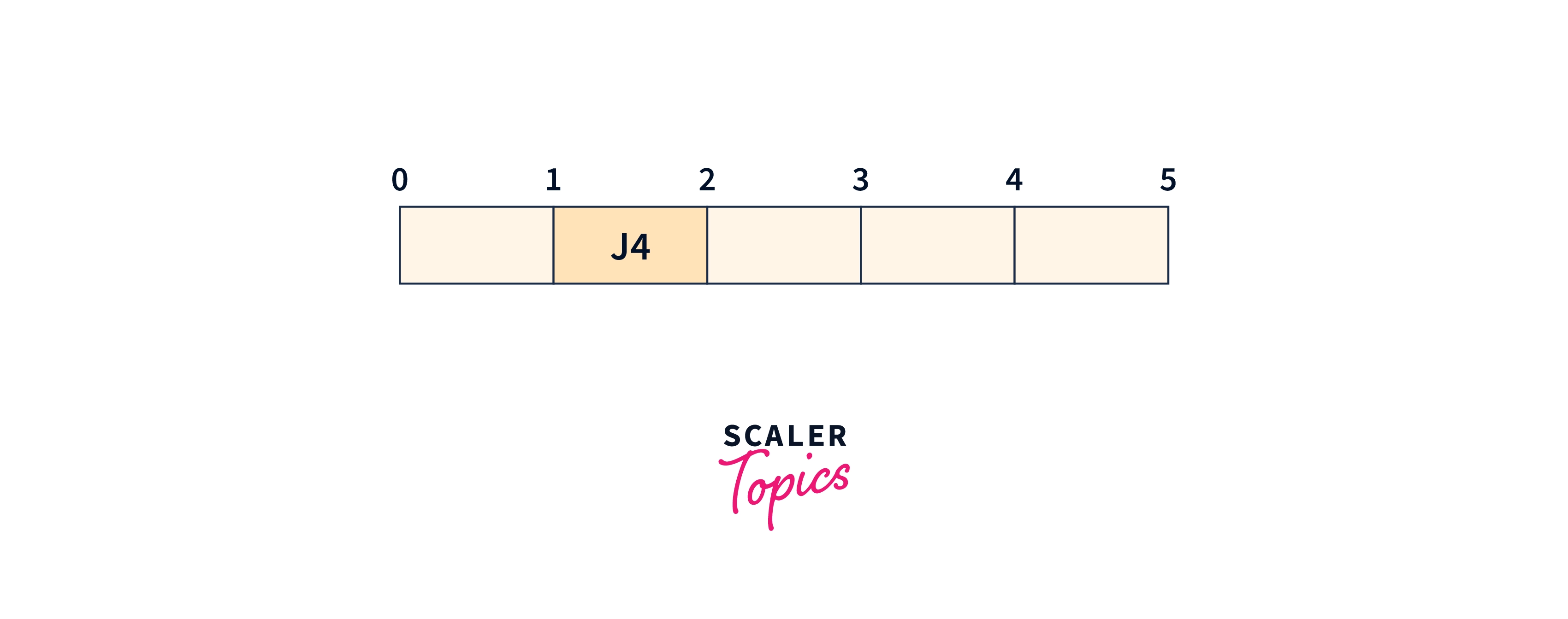
Now, pick the jobs one by one as presented in step, 1, and place them on the Gantt chart as far as possible from 0.
We will pick Job 4. Its deadline is 2. So placing the job in the empty slot available just before the deadline.
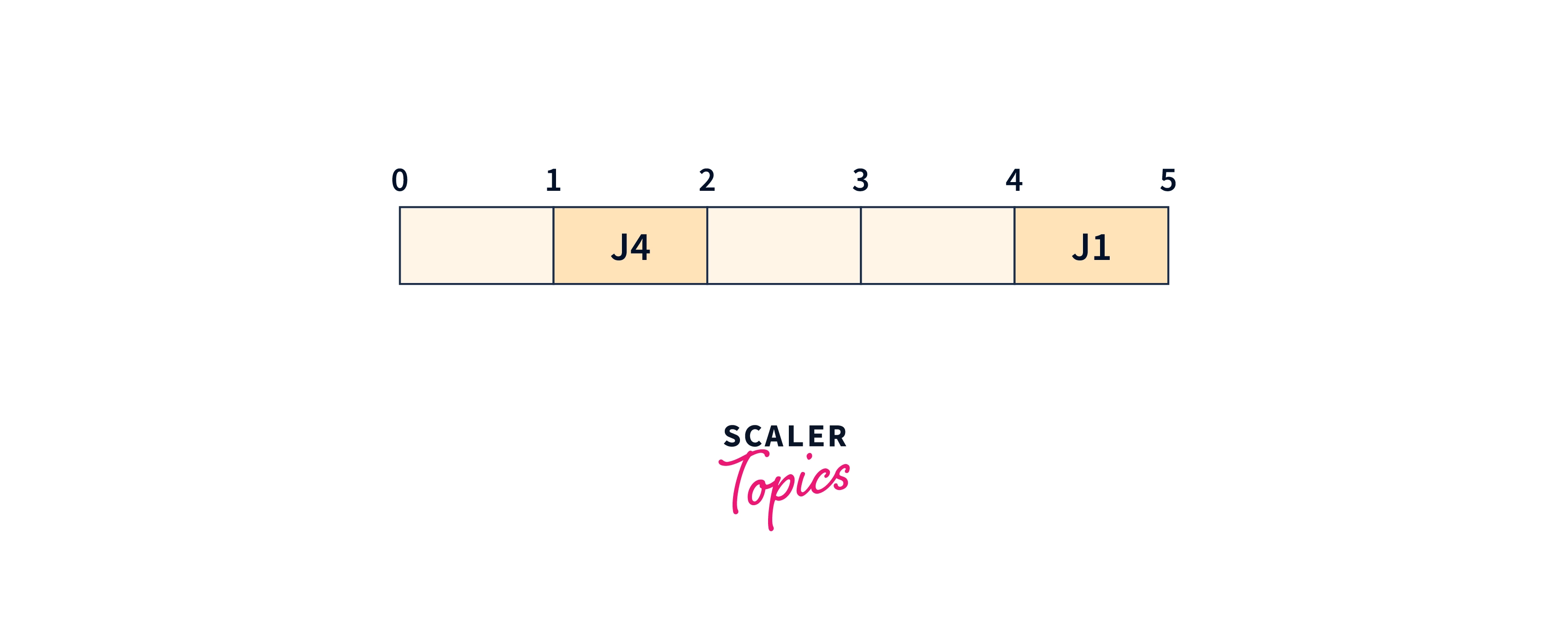
We will now pick Job 1. Its deadline is 5. So placing the job in the empty slot available just before the deadline.
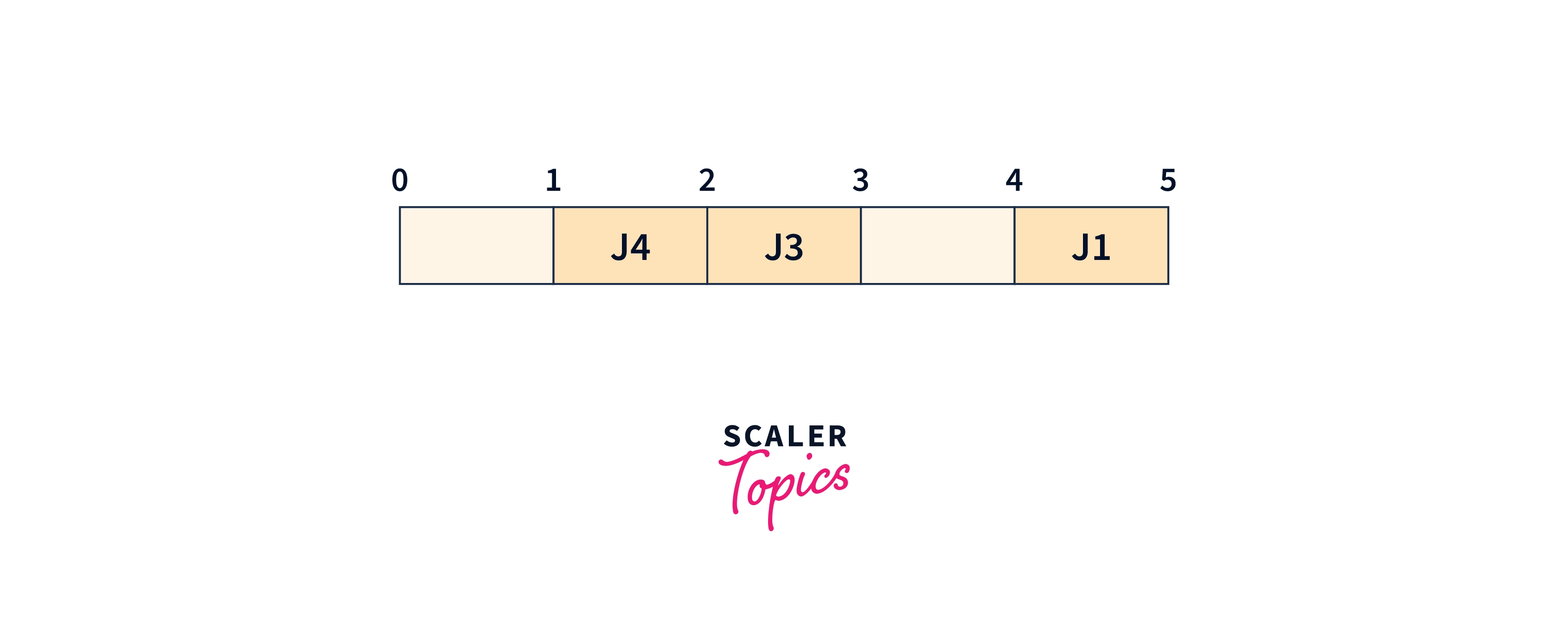
We will now pick Job 3. Its deadline is 3. So placing the job in the empty slot available just before the deadline.
We will now pick Job 2. Its deadline is 3. Here second and third slots are already filled. So place job 2 on the next available free slot farthest from 0, i.e first slot.
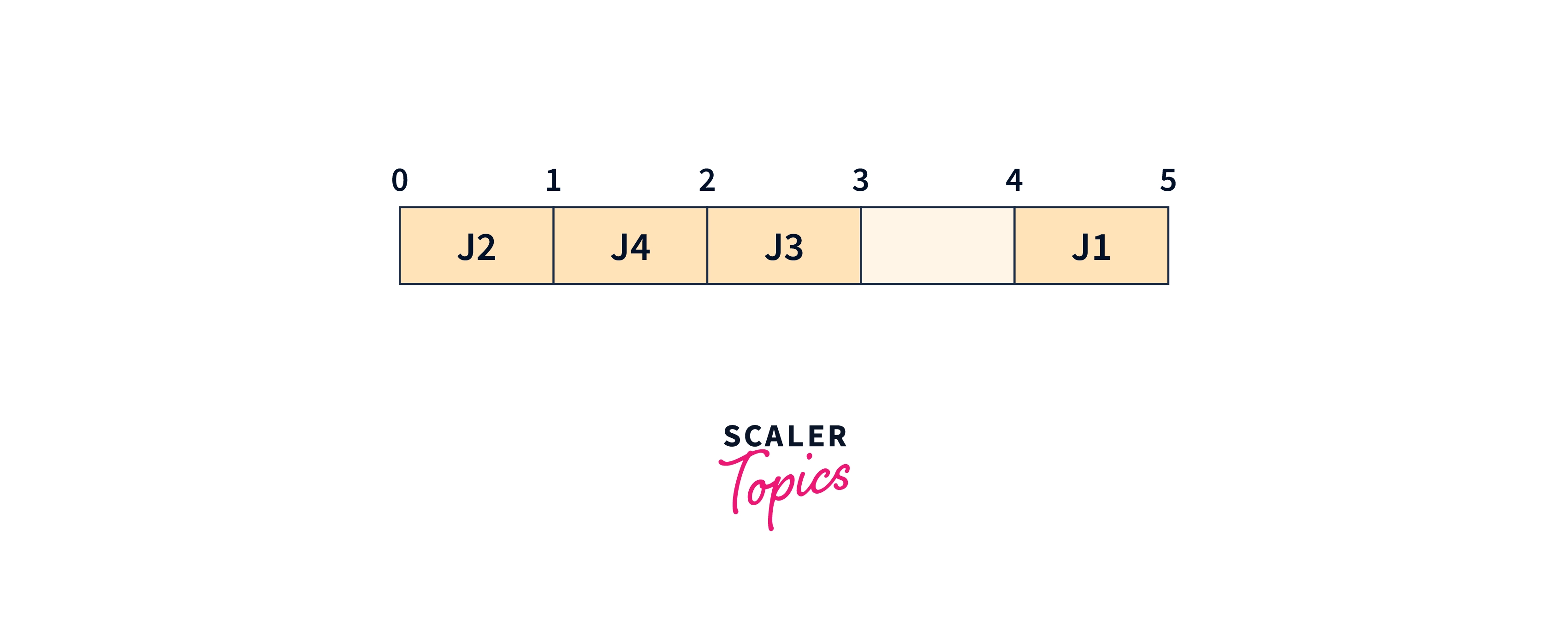
We will now pick Job 5. Its deadline is 4. Place the job in the first empty slot before the deadline,i.e fourth slot.
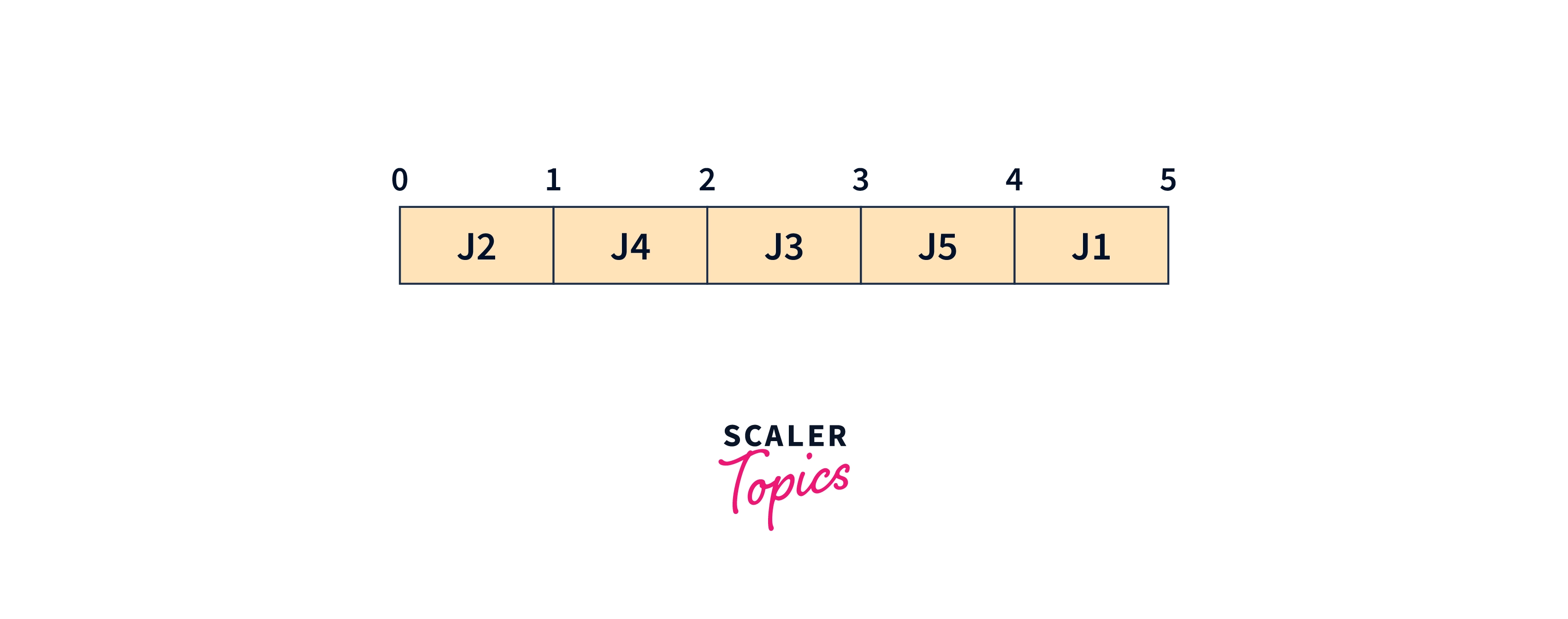
We will now pick Job 6. Its deadline is 2. Now we need to place the job in the first empty slot before the deadline. Since, no such slot is available, hence Job 6 can not be completed.
So, the most optimal sequence of jobs to maximize profit is Job 2, Job 4, Job 3, Job 5, and Job 1.
And the maximum profit earned can be calculated as:
Profit of Job 2 + Profit of Job 4 + Profit of Job 3 + profit of Job 5 + profit of Job 1
Analysis
There can be many sequences possible for this problem, but to get the most optimal sequence, we implement the Greedy approach.
We observed that to get the maximum profit, we try to execute the jobs of maximum profit in the free time interval available just before their deadline so that we can have the space left for the jobs with lesser deadlines.
In this way, we can get the most optimal sequence of the jobs providing a maximum profit.
Examples for Job Sequencing with a Deadline:
| Jobs | Profit | Deadline |
|---|---|---|
| J1 | 85 | 5 |
| J2 | 25 | 4 |
| J3 | 16 | 3 |
| J4 | 40 | 3 |
| J5 | 55 | 4 |
| J6 | 19 | 5 |
| J7 | 92 | 2 |
| J8 | 80 | 3 |
| J9 | 15 | 7 |
Solution:
Step 1:
Sort the jobs in decreasing order of profit.
| Jobs | Profit | Deadline |
|---|---|---|
| J7 | 92 | 2 |
| J1 | 85 | 5 |
| J8 | 80 | 3 |
| J5 | 55 | 4 |
| J4 | 40 | 3 |
| J2 | 25 | 4 |
| J6 | 19 | 5 |
| J3 | 16 | 3 |
| J9 | 15 | 7 |
Step 2:
The value of the Maximum Deadline is 7. So, draw the Gantt chart up to the maximum deadline.
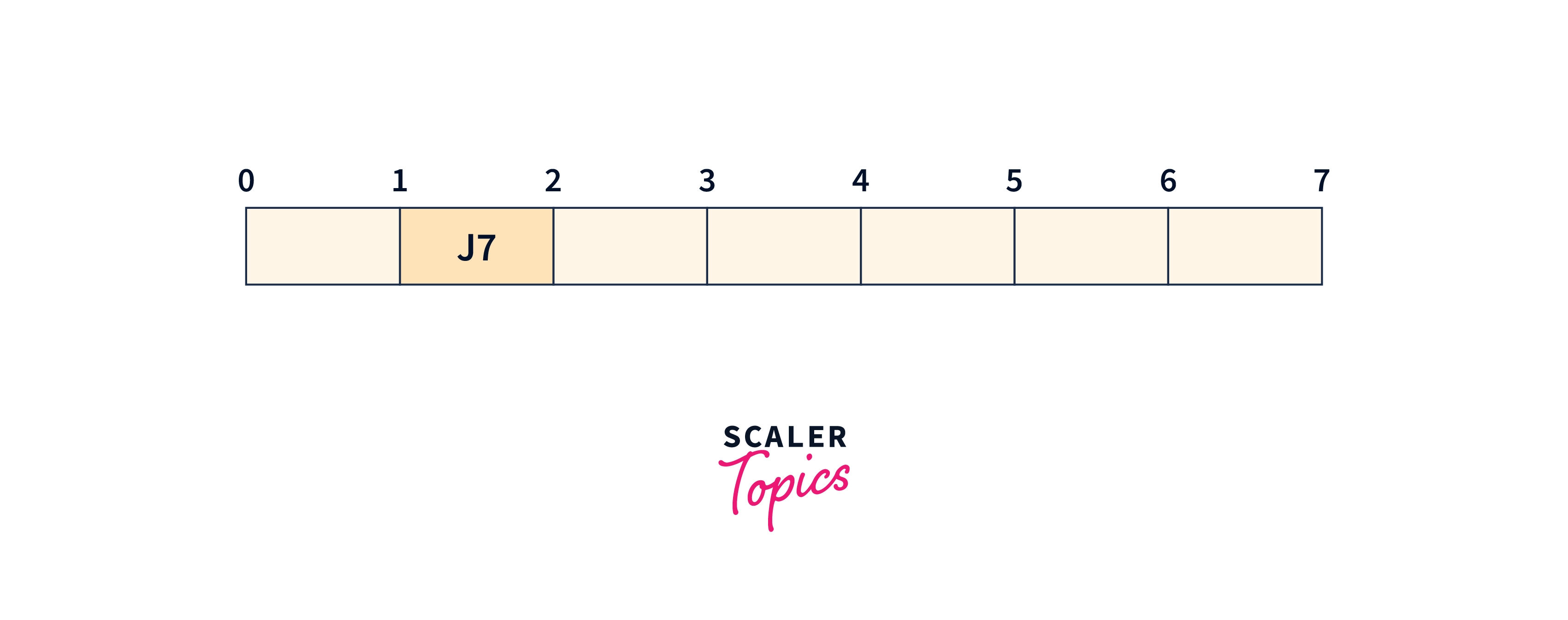
Step 3: One by one pick the job from the table formed in Step 1 and place it in the first empty slot available just before the deadline and as far as possible from 0.
We will take the J7 job
We will take the J1 job
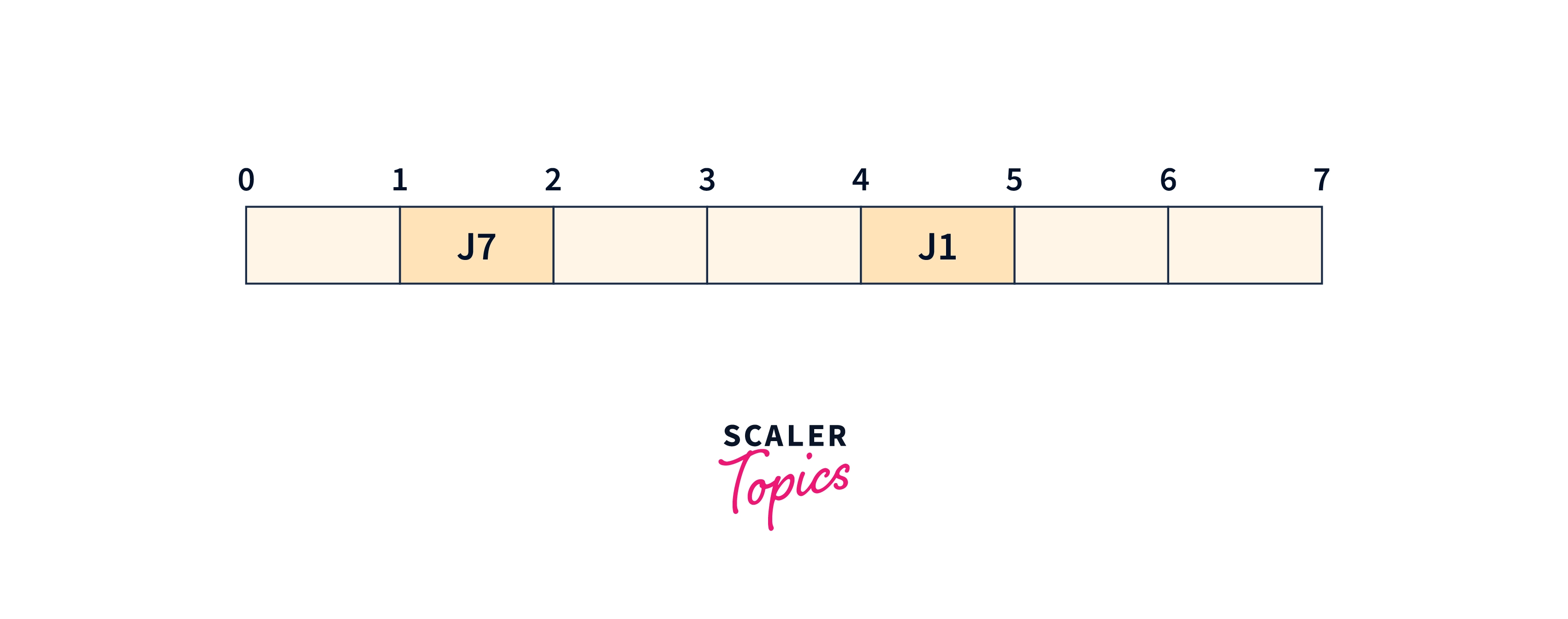
We will take the J8 job
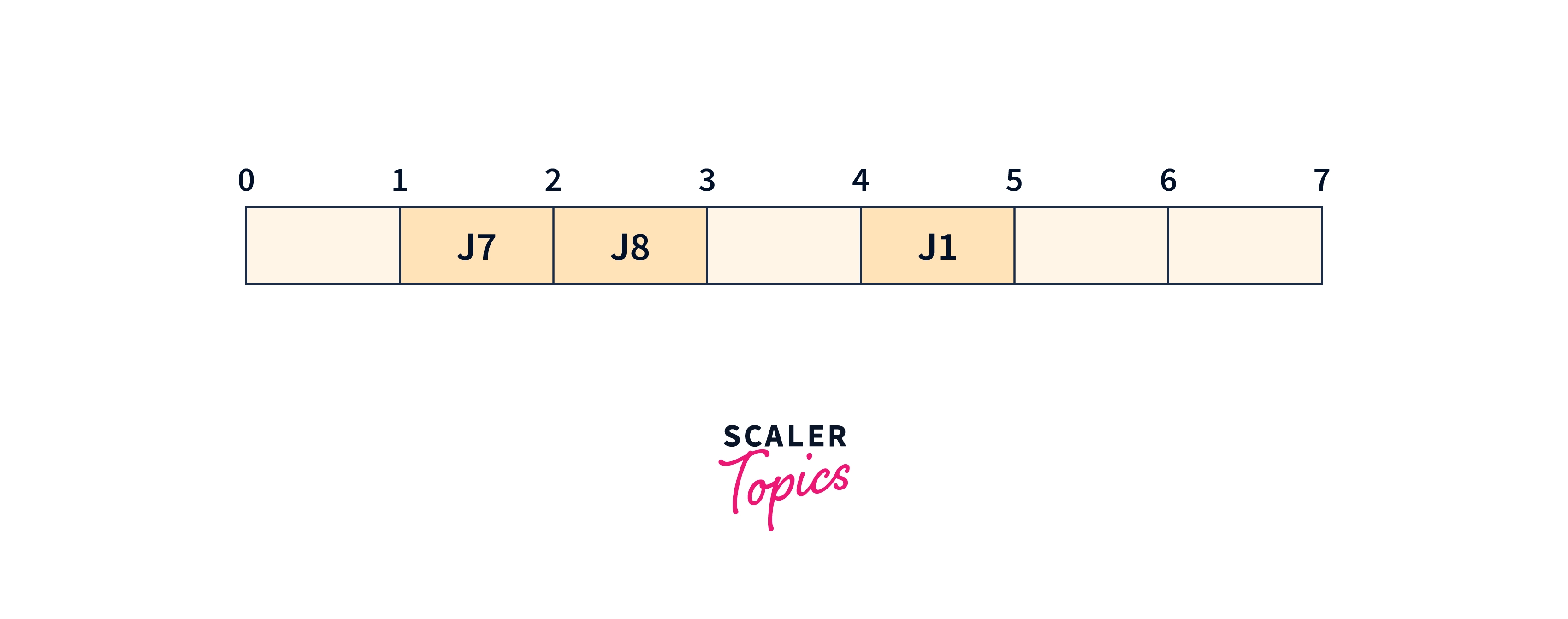
We will take the J5 job
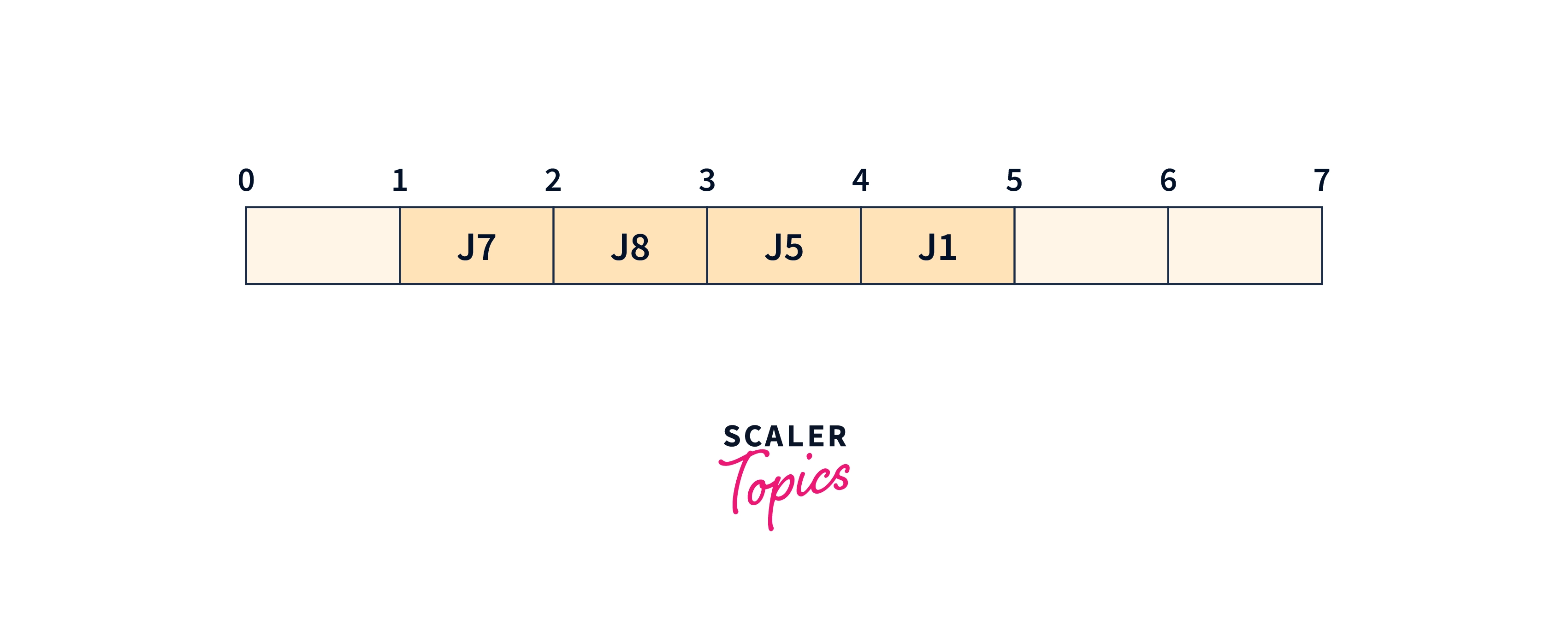
We will take the J4 job
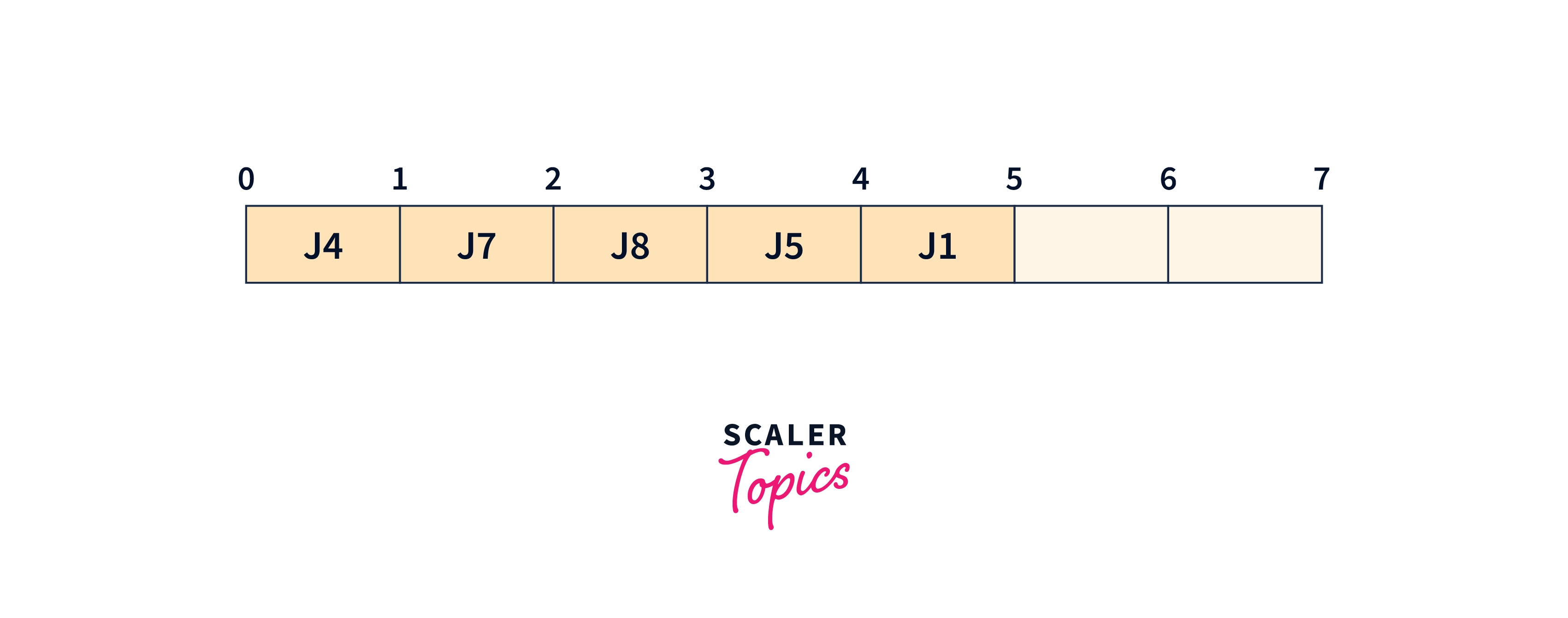
We can't take J2, J3, and J6 jobs as no empty slots are available before their respective deadlines.
We will take the J9 job
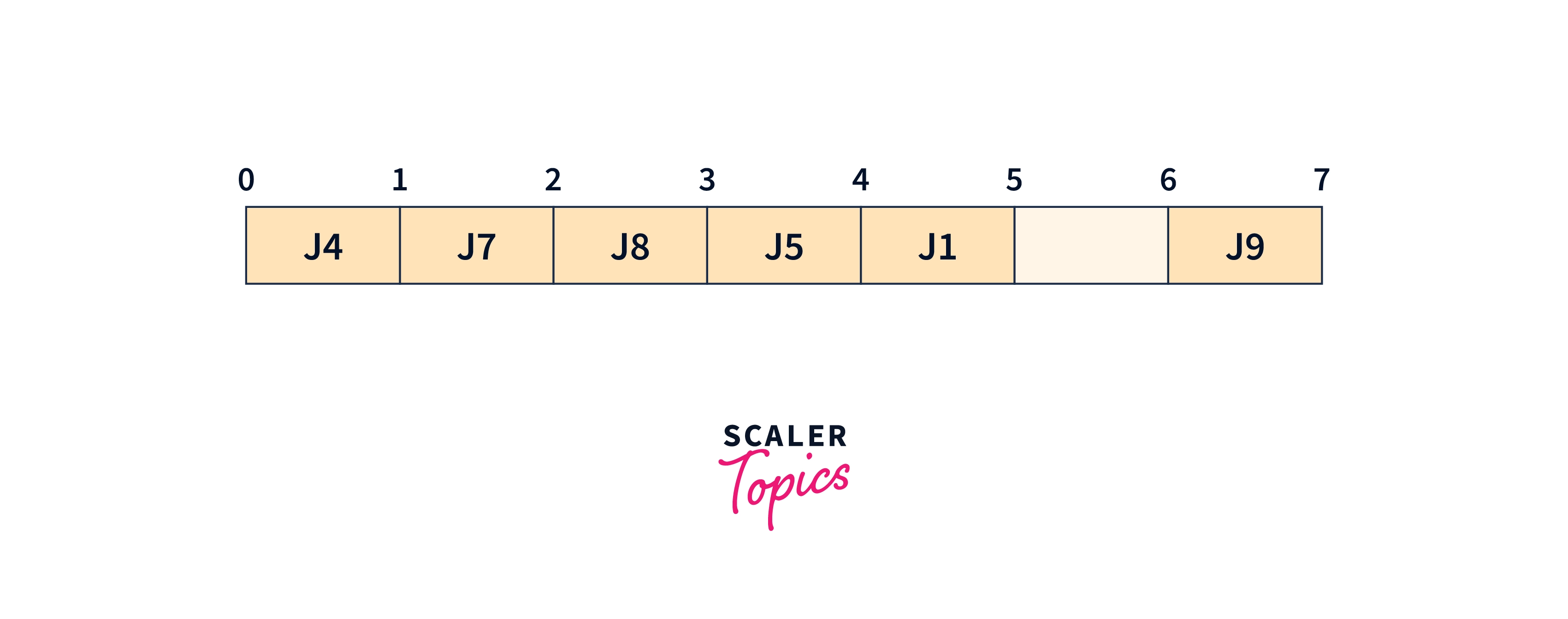
The optimal sequence is J4, J7, J8, J5, J1, and J9.
And the maximum profit earned is
Conclusion
- Job Sequencing with Deadlines is a problem to find the most optimal sequence of Jobs when executed in a single processor operating system, to obtain the maximum profit.
- There are many sequences of Jobs possible, Since we need the most optimal sequence, hence it is a greedy problem.
- A greedy algorithm is an approach for solving optimization problems by selecting the best option available at the moment.
- The greedy method involves sorting the jobs in decreasing order of their profit and then placing the jobs one by one in the free slot available just before the deadline to give the maximum profit.
- In real life, job scheduling algorithms are widely used in the fields of optimal routing in networks.
- In the job sequencing problem, only one processor is available for processing all the jobs and it takes one unit of time to complete a job.
