Recursion in Kotlin

Introduction

A function that invokes itself is referred to as a recursive function in kotlin, and this approach is termed recursion.

Within the given program, two categories of function calls exist:

• Regular function calls
• Recursive function calls

When the printHello() function is called from the main() function, it's considered a standard function call. However, when the printHello() function is called from within another instance of itself, it qualifies as a recursive function call. This is due to the fact that the printHello() function is calling upon its own definition.

How does recursion in kotlin work in?

Visual Explanation:

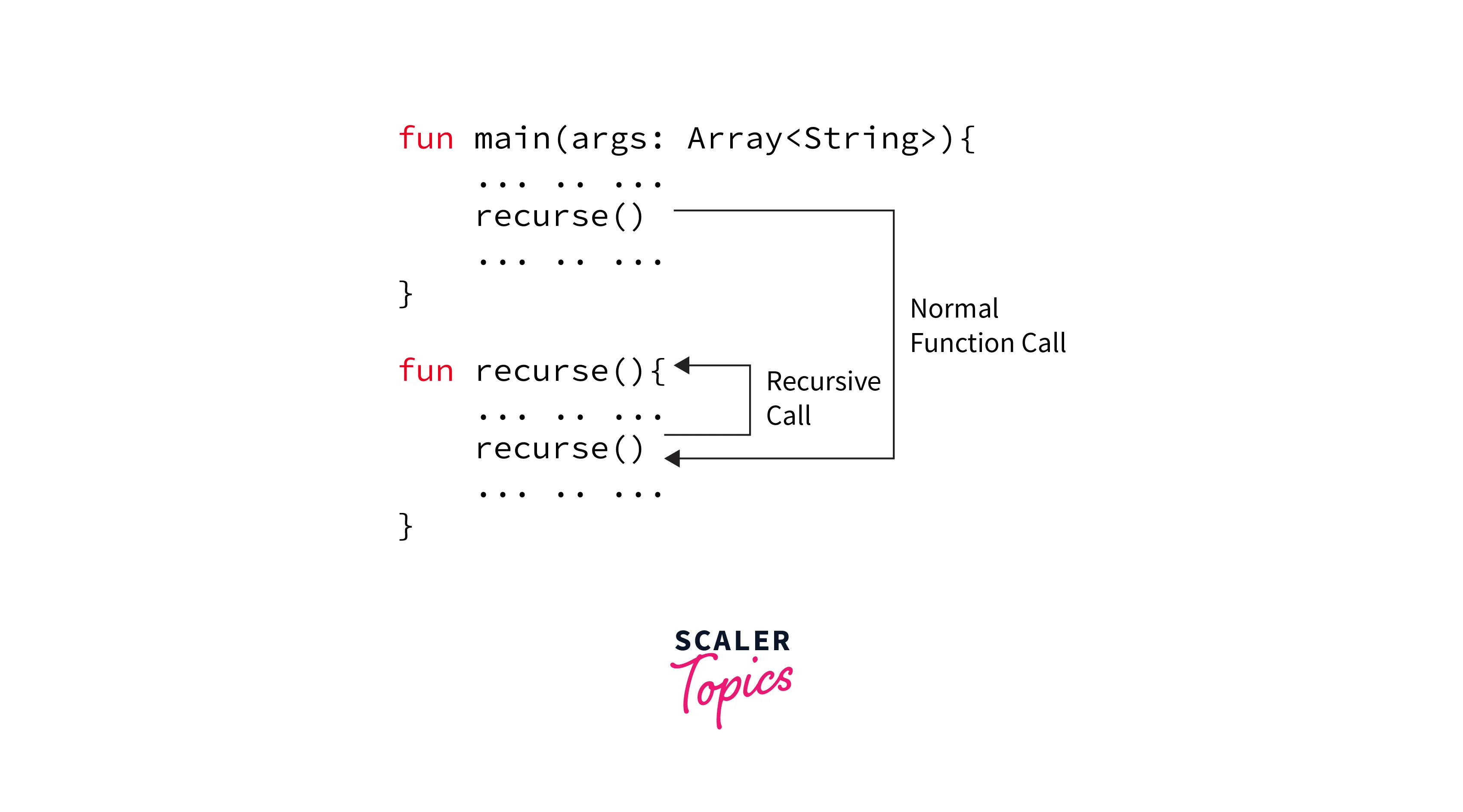
Here, the recursive call continues forever causing infinite recursion.

To avoid infinite recursion in kotlin, if...else (or similar approach) can be used where one branch makes the recursive call and other doesn't this leads us to,

Recursion Function Examples

Let us take a look at few examples to understand the concept of recursion better.

Example 1: Find the Factorial of a Number Using General Recursion

Output:

Visual explanation:

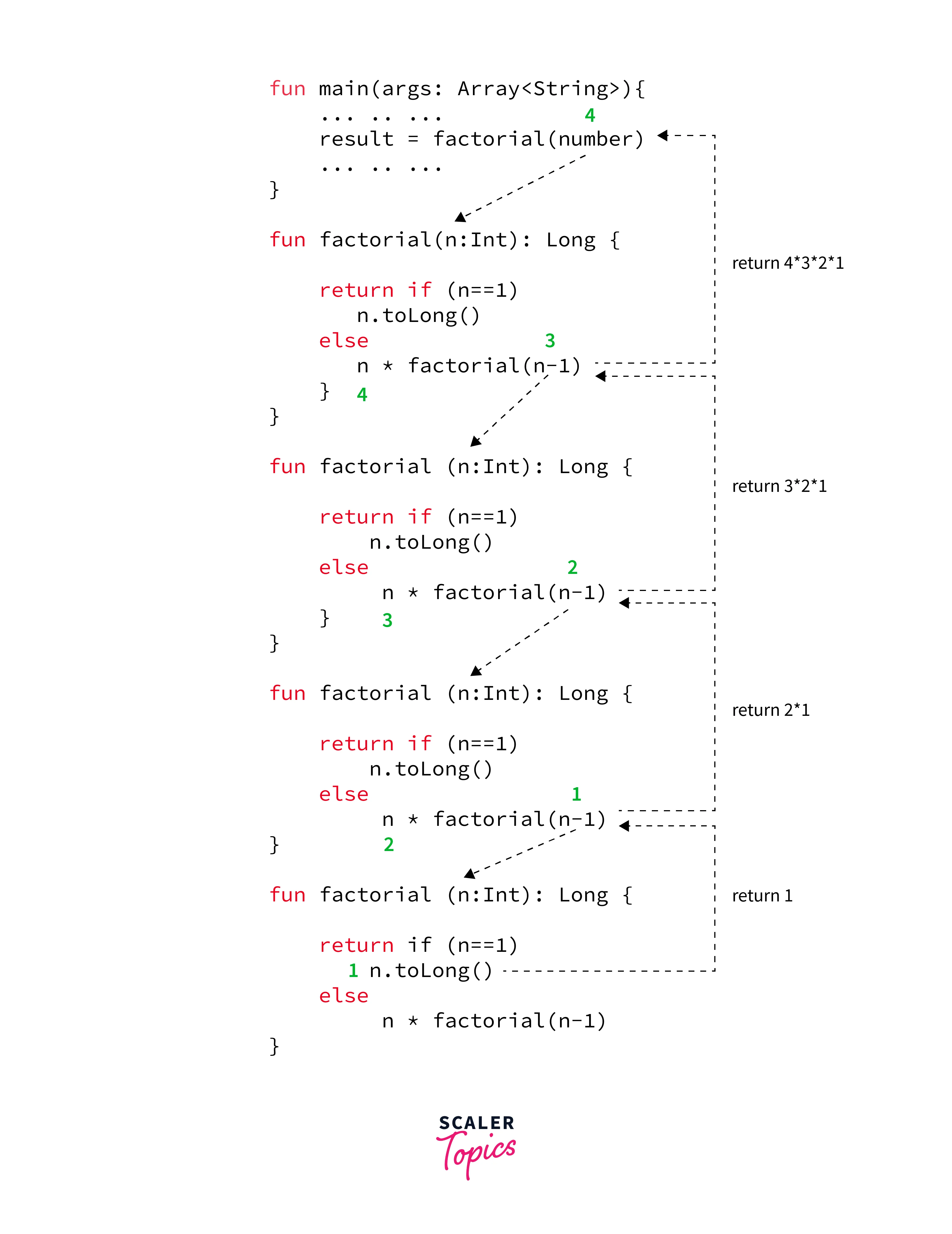
Steps:

factorial(4)              // 1st function call. Argument: 4
4*factorial(3)            // 2nd function call. Argument: 3
4*(3*factorial(2))        // 3rd function call. Argument: 2
4*(3*(2*factorial(1)))    // 4th function call. Argument: 1 
4*(3*(2*1))                 
24

Example 2: Find the Factorial of a Number Using Tail Recursion

The example to compute factorial of a number in the above example cannot be optimized for tail recursion.

Here's a different program to perform the same task.

Code:

Output:

Explanation: The compiler can optimize the recursion in this program as the recursive function is eligible for tail recursion, and we have used tailrec modifier that tells compiler to optimize the recursion. tailrec is a Kotlin keyword that indicates that this function is tail-recursive. Tail recursion is a special form of recursion where the recursive call is the last operation performed in the function. This allows the Kotlin compiler to optimize the recursion into an iterative loop, avoiding stack overflow errors for large inputs.

The code as a whole calculates the factorial of the number 5 and prints the result, which is 120 (5 factorial).

Example 3: Find the Sum of Elements of an Array Using Recursion

Code:

Output:

Explanation: Here, we have initialized an array and passed as an argument to the sum() function. In each recursive call the index value decrement by one. If the index equal to zero or less than then terminate it and return the sum of all the elements.

Tail Recursion

Tail recursion is a universal concept that isn't exclusive to the Kotlin language. Several programming languages, Kotlin included, leverage tail recursion to enhance the efficiency of recursive calls. However, there are languages like Python that lack support for tail recursion.

a. General vs Tail Recursion

In regular recursion, you initiate all the recursive calls beforehand and derive the final result from the returned values afterward. Consequently, the result is not available until all recursive calls are executed.

Utilizing tail recursion offers specific advantages. For instance, tail recursion conserves stack space for subsequent recursive calls. This is possible because there's no requirement to retain the current function call in the stack memory, primarily due to the fact that the recursive call takes place at the conclusion of the function. In the context of tail recursion programs, issues such as StackOverflowError are averted.

Condition for tail recursion A recursive function qualifies as having tail recursion when its self-invoking function call is the final operation it undertakes.

Let's see some examples,

Example 1: Ineligible for tail recursion due to the fact that the function call to itself, n * factorial(n-1), does not constitute the final operation.

Example 2: Qualified for tail recursion as the function's self-invoking call, fibonacci(n-1, a+b, a), stands as the concluding operation.

In Kotlin, to instruct the compiler to execute tail recursion, it's necessary to annotate the function with the tailrec modifier.

Advantages and Disadvantages of Recursion in Kotlin

Advantages:

1. Enhanced code readability and maintainability: Recursive functions frequently lead to more succinct and comprehensible code, particularly when tackling intricate issues.
2. Simple algorithm implementation: Numerous algorithms, like the Tower of Hanoi, lend themselves to straightforward implementation through recursion.
3. Promotes reusability: Recursive functions are often reusable for comparable problems, curtailing the necessity of crafting new code.
4. Adaptability to dynamic data structures: Recursive algorithms can harmonize effectively with dynamic data structures that expand or contract during runtime, showcasing an ability to adjust to structural changes.

Disadvantages:

• Elevated memory consumption: Each recursive call introduces a fresh function entry to the call stack, potentially triggering stack overflow issues when managing substantial datasets.
• Performance implications: Recursive algorithms frequently exhibit inferior performance compared to their iterative counterparts, demanding more memory and CPU cycles.
• Constraints of Tail Recursion Optimization: While Kotlin integrates tail call optimization, a mechanism mitigating certain tail-recursive call overheads, this optimization might not be universally applicable to all recursive functions.
• Complex debugging process: Debugging recursive functions can pose considerable difficulties. Missteps in implementation can lead to predicaments such as endless recursion or flawed base cases, resulting in intricate debugging challenges.