Program to Calculate the Levenshtein Distance in List in Python

What is Levenshtein Distance?

Have you ever wondered how word processors like MS Word and Google Docs can identify misspelled words and provide suggestions? These word processors use multiple string algorithms to match each word written by the user against the words in their dictionary. Now, identifying misspelled words can be done using a standard String Matching algorithm. However, to provide suggestions, the processors need to find a list of such words that are close similar to the misspelled word. In simpler words, the processor needs an algorithm that computes the similarity between two words. This can be calculated by finding the Levenshtein Distance between the two strings.

Levenshtein Distance (a.k.a Edit Distance) calculates the distance between two words and returns a number representing how similar the words are. The number represents the total number of edits required to transform one word into another. There are three ways by which the editing can be done:

• Insertion A new character can be inserted anywhere in the given string. Example: A: "helo" B: "hello" We can insert the character 'l' at position 4 in string A to get string B.
• Deletion A character can be deleted from anywhere in the given string. Example A: "helloo" B: "hello" We can delete a character at position 6 in string A to get string B.
• Replacement A character can be replaced with the other character. Example A: "hella" B: "hello" We replace the character 'a' with 'o' at position 5 in string A to get the string B.

Each of these operations adds 1 to the edit distance.

Understanding the Levenshtein Algorithm

Problem Statement

Consider two input strings A and B of length n and m respectively, containing lowercase English letters only. The problem is to find the Levenshtein distance between A and B using the following edits:

• Insert a character in A
• Delete a character from A
• Replace a character in A with any other character.

The cost of each operation is 1.

Algorithm (Using sub-subproblems)

Levenshtein distance between two strings can be found using dynamic programming. The algorithm exhibits the property of overlapping subproblems.

Consider the strings A and B.

• Case 1: $A[1] = B[1]$. In this case, we can skip the first position and the edit distance of the whole problem is equal to the edit distance of $A[2:n]$ and $B[2:m]$. Here $S[i:j]$ means substring of $S$ from position $i$ to position $j$.
• Case 2: $A[1] \neq B[1]$. In this case, we will use the three operations mentioned above to find the edit distance.
  • Insert $B[1]$ in $A$: The edit distance is equal to 1 + the edit distance of $A[1:n]$ and $B[2:m]$. This is because the first character in $B$ matches the newly added first character in $A$.
  • Delete $A[1]$: The edit distance is equal to 1 + the edit distance of $A[2:n]$ and $B[1:m]$. This is because we have simply deleted the first character in $A$. The characters left in both strings will contribute to the edit distance of the whole problem.
  • Replace $A[1]$ with $B[1]$: The edit distance will be equal to 1 + the edit distance of $A[2:n]$ and $B[2:m]$. The edit distance will be the minimum cost of inserting, deleting, or replacing the characters in $A$ to get the string $B$.

The general idea of the algorithm is to transform the prefix of string $A[1:i]$ equal to the prefix of string $B[1:j]$ using the minimum number of insert, delete and replace operations. At every mismatch, we need to apply the three types of edit and choose the operation that minimizes the overall edit distance of the problem.

Example

Let us consider an example where $A$ = "gate" and $B$ = "goat". To calculate the Levenshtein distance, we will use the above approach.

• $A$ = "gate" and $B$ = "goat". Since $A[1] = B[1]$, we simply move to the next character.
• Since $A[2] \neq B[2]$, we have three choice. If we perform:
  • Insert: We get $A$ = "goate" and $B$ = "goat".
  • Delete: We get $A$ = "gte" and $B$ = "goat".
  • Replace: We get $A$ = "gote" and $B$ = "goat".

Now if we look at the choice where we insert an element, we see that deleting the last character from $A$ = "goate" will transform it into the string B. Hence in this case the edit distance will be $2$. In the rest cases, we see that the number of operations will be more, so we take the minimum of the three cases. Edit Distance of $A$ = "gate" and $B$ = "goat" is $2$.

Understand the Array

Now to efficiently compute the result, we need to add memoization in the above algorithm. To do this, we need some states to define a subproblem uniquely. To identify a subproblem, we only need to know the length of the prefix of string $A$ and string $B$. Hence we need two variables $i$ and $j$, to define our dynamic programming states. Let us define $DP[i][j]$ = Levenshtein distance of string $A[1:i]$ and string $B[1:j]$.

Base Case: In the base case, we can consider that the length of one of the strings is $0$. In this case, we will either use only insert operations, if the length of $A$ is $0$, or else we will use only delete operations if the length of string $B$ is $0$. $DP[0][j] = j$ for all $j$ from $1$ to $m$. $DP[i][0] = i$ for all $i$ from $1$ to $n$.

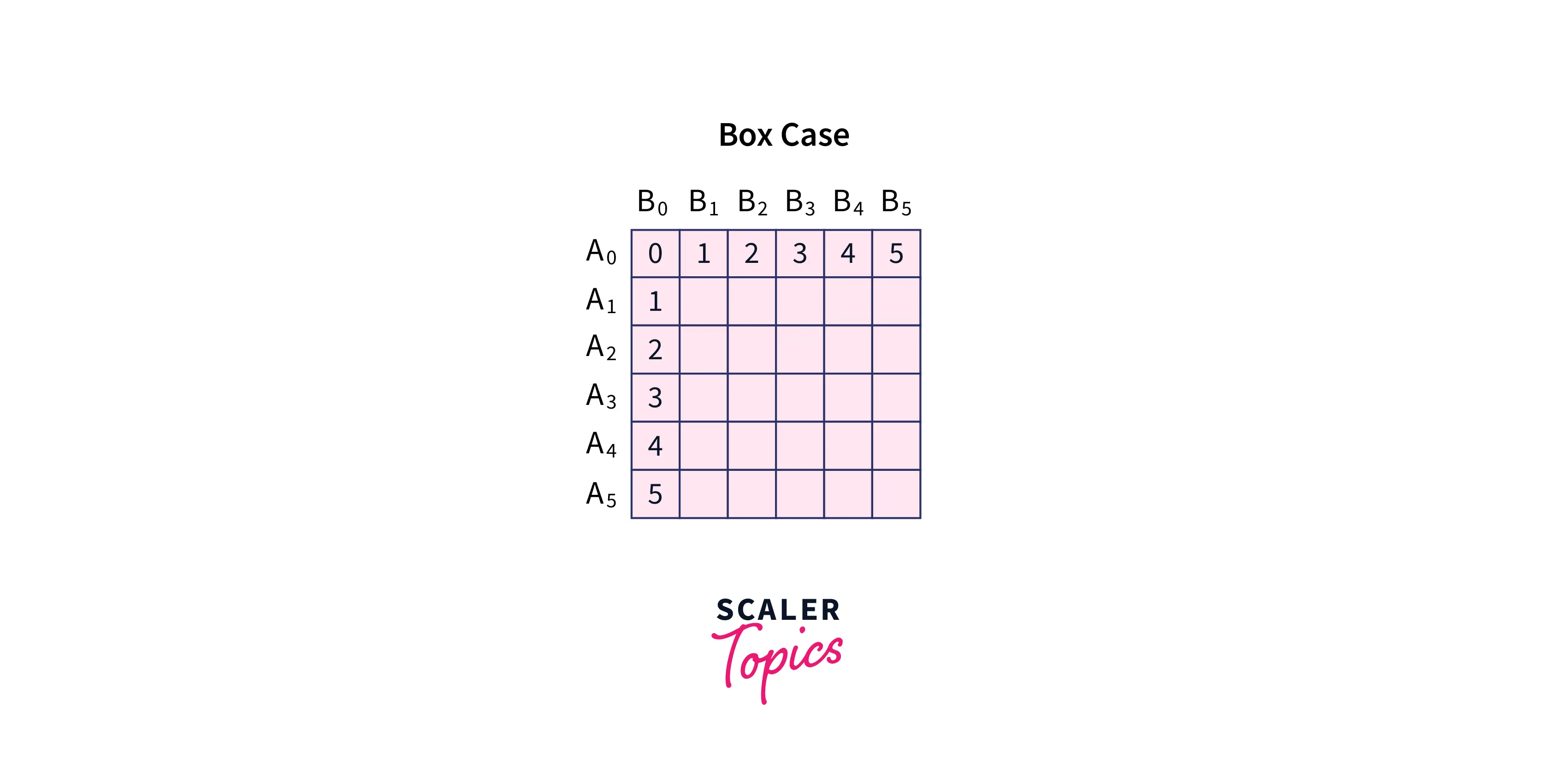
Transitions

Suppose we want to calculate the edit distance of $A[0:i]$ and $B[0:j]$, then

• Case 1: $A[i] == B[j] \Rightarrow DP[i][j] = DP[i-1][j-1]$
• Case 2: $A[i] \neq B[j]$. In this case, we need to perform an edit operation.
  • If we perform insert operation then we will take $i-1$ characters from $A$ and $j$ characters from $B$, so $DP[i][j] = 1 + DP[i-1][j]$.
  • If we perform delete operation then we have not matched the $j^{th}$ character in B yet, so we simply carry forward the edit distance calculated till $i^{th}$ character of $A$ and $(j-1)^{th}$ character of $B$, so $DP[i][j] = 1 + DP[i][j-1]$.
  • If we do a replace, then $DP[i][j] = 1 + DP[i-1][j-1]$, as we have replaced $i^{th}$ character of $A$ with $j^{th}$ character of $B$.

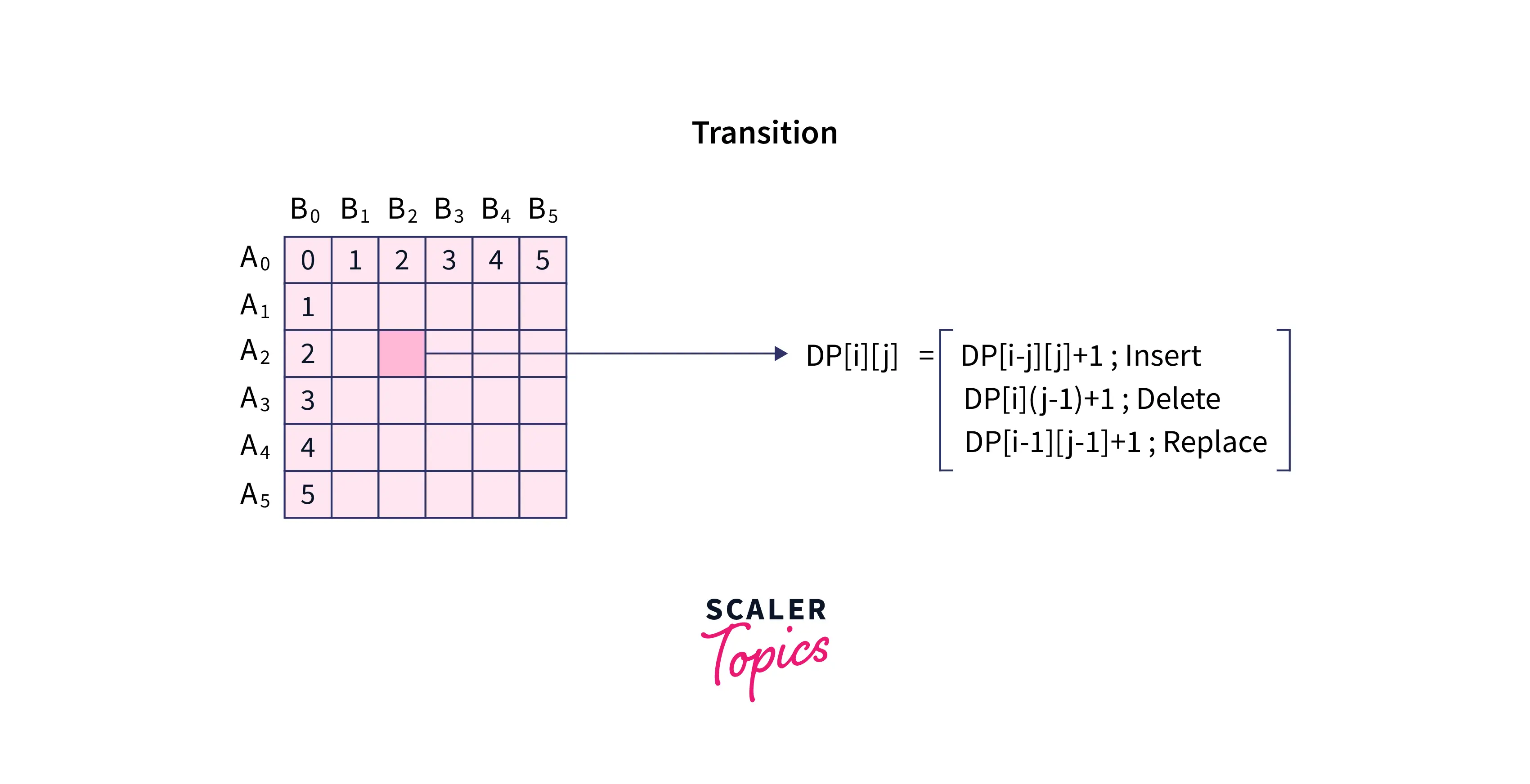
Finally, we write $DP[i][j] = 1 + min\{DP[i-1][j], DP[i][j-1], DP[i-1][j-1]\}$

Final Output After we calculate all the transitions, the Levenshtein Distance will be equal to $DP[N][M]$.

Example

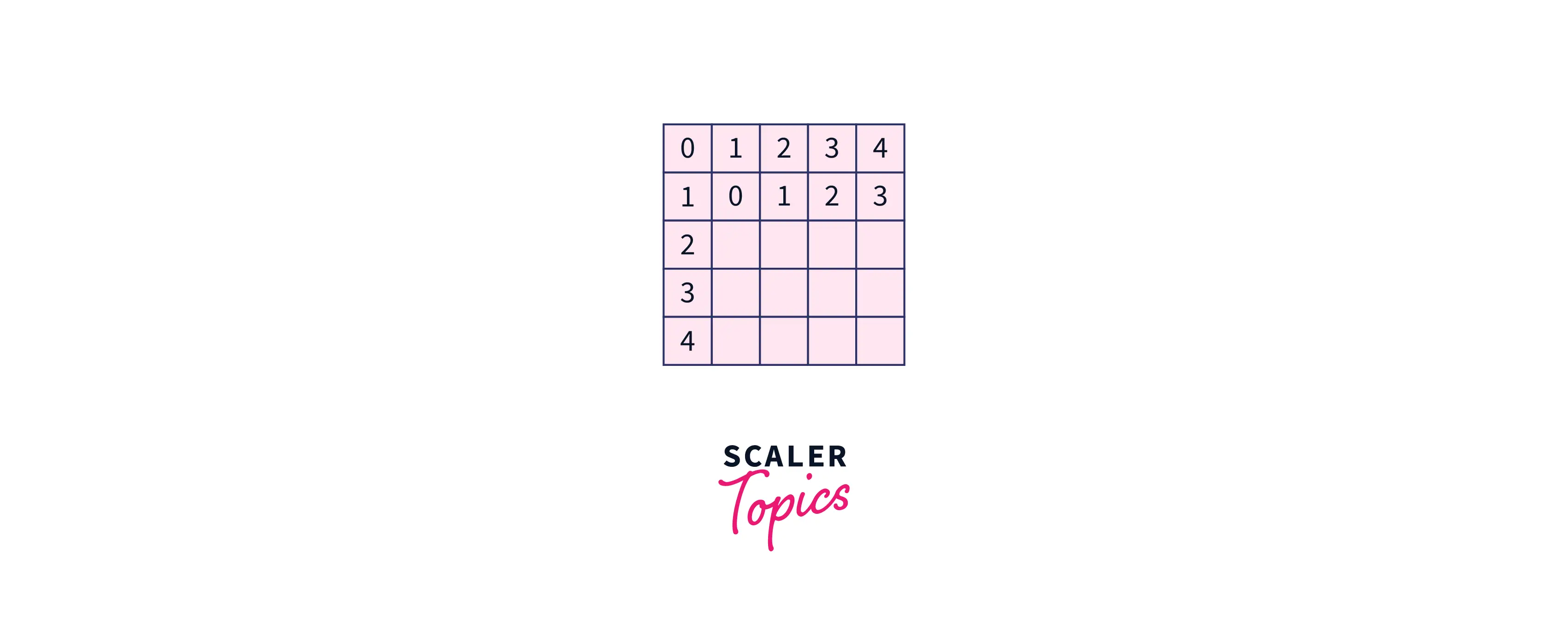
Let us look at the $DP$ matrix for $A$ = "gate" and $B$ = "goat". Here $n = m = 4$. Consider $i = 0$ and $j = 0$ be the iterators. When $i = 1$ and $j = 1 .. m$ we calculate the edit distance for $A[1]$ with all the prefixes of $B$. Since $A[1] == B[1]$, $DP[1][1] = DP[i-1][j-1] = 0$. Since $B[2]$ is an extra character, a delete operation is required, $DP[1][2] = DP[1][1] + 1 = 2$. In this way, we build the rest of the matrix.

When $i = 2$ and $j = 1 .. m$, we calculate the edit distance for $A[1:2]$ with all prefixes of $B$.

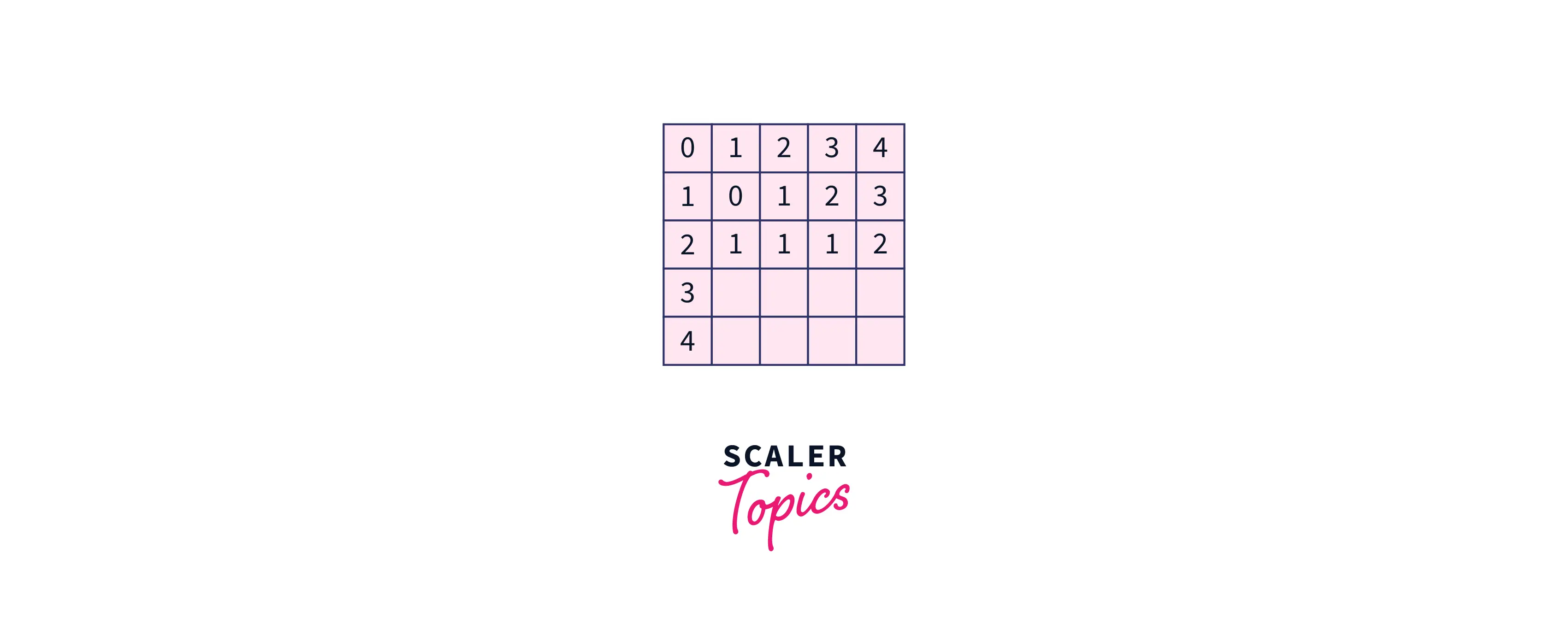
Repeating the same process, we will end up with the whole $DP$ matrix.

Implementation

Output

Complexity Analysis of Levenshtein Algorithm

Time Complexity

In the implementation, we have a $n*m$ state, and for each transition, we take $O(1)$ time, hence the time complexity is $O(n*m)$ where $n$ and $m$ are the lengths of strings $A$ and $B$ respectively. Time Complexity: $O(n*m)$

Space Complexity

In the implementation, we use a table to store $n*m$ states of the problem, hence the space complexity is $O(n*m)$ where $n$ and $m$ are the lengths of strings $A$ and $B$ respectively. Space Complexity: $O(n*m)$

Calculating the Levenshtein Distance using Enchant

Introduction

Spell Checking in Python is also implemented in the in-built module pyenchant. This module can be used to calculate the Levenshtein distance between two strings. To download this package, run the following command in the terminal:

Algorithm

The following function pyenchant.utils.levenshtein() can be used to calculate the edit distance between two strings. This function is a library implementation of the above-discussed algorithm.

Example

Output