Linear Regression Vs Logistic Regression

Linear regression vs logistic regression - these are two fundamental algorithms in the realm of machine learning, each tailored to address specific types of predictive tasks and data characteristics. While linear regression is ideal for predicting continuous outcomes, logistic regression excels in binary classification scenarios. Let's delve deeper into the nuances of each and understand their differences to effectively leverage them in various applications.

Linear Regression in Machine Learning

linear regression example

Linear regression is a supervised learning algorithm used for predicting the value of a continuous dependent variable based on one or more independent variables. It establishes a linear relationship between the input variables (predictors) and the output variable (target). The algorithm finds the best-fitting straight line through the data points to make predictions. Linear regression is extensively used in various fields such as economics, finance, engineering, and social sciences for tasks like sales forecasting, risk assessment, and trend analysis.

Linear regression aims to model the relationship between a dependent variable $y$ and one or more independent variables $x$ by fitting a linear equation to observed data. The equation for simple linear regression with one independent variable can be expressed as:

$[ y = \beta_0 + \beta_1x + \epsilon ]$

Where:

$y$ represents the dependent variable, which is the variable we aim to forecast or predict.
$x$ stands for the independent variable, which is the variable utilized for prediction or forecasting.
$\beta_0$ is the intercept (the value of $y$ when $x$ is 0).
$\beta_1$ is the slope (the change in $y$ for a one-unit change in $x$ ).
$\epsilon$ is the error term, representing the variability in $y$ that is not explained by $x.$

In the case of multiple linear regression with $n$ independent variables, the equation becomes:

$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n + \epsilon$

The objective of linear regression is to estimate the coefficients $\beta_0, \beta_1, ..., \beta_n$ that minimize the sum of squared residuals (least squares method). This is typically achieved using optimization techniques such as gradient descent or matrix factorization methods.

To explore linear regression in detail, you can refer to this link.

Logistic Regression

logistic regression

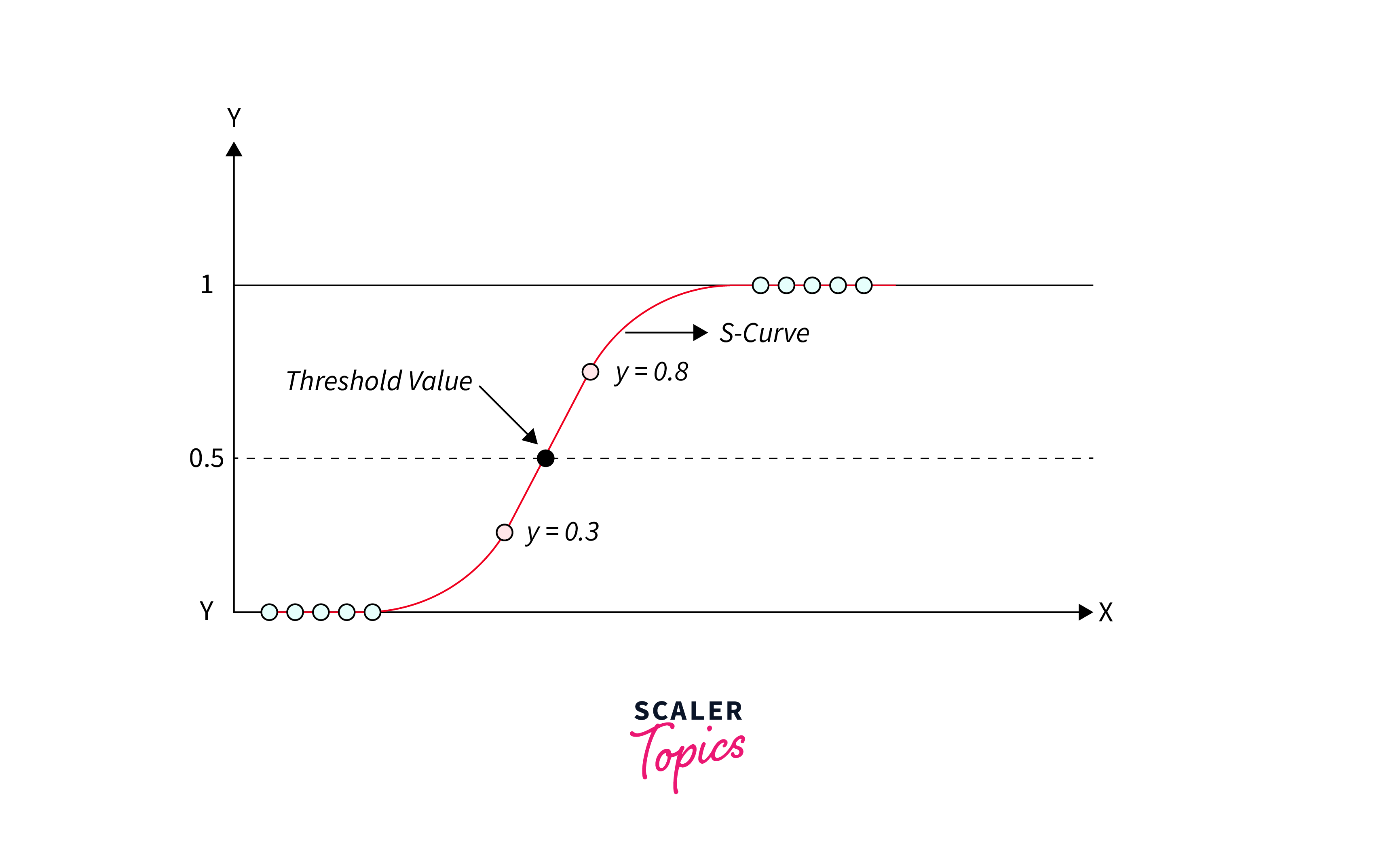
Logistic regression, despite its name, is a classification algorithm used for predicting the probability of occurrence of a binary event based on one or more independent variables. Unlike linear regression, which predicts continuous outcomes, logistic regression predicts probabilities and assigns observations to discrete categories (usually binary: 0 or 1). It employs the logistic function (also known as the sigmoid function) to map predicted values between 0 and 1, making it suitable for binary classification tasks. Logistic regression finds applications in various domains such as healthcare (disease diagnosis), marketing (customer churn prediction), and fraud detection.

Logistic regression models the probability of a binary outcome (usually coded as 0 or 1) based on one or more independent variables. It uses the logistic function (sigmoid function) to transform the output of a linear combination of the independent variables into probabilities between 0 and 1. The logistic function is defined as:

$\sigma(z) = \frac{1}{1 + e^{-z}}$

Where:

$z = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n$ is the linear combination of independent variables.
$\beta_0, \beta_1, ..., \beta_n$ are the coefficients (similar to linear regression).
$e$ is the natural logarithmic base.

The output of the logistic function $\sigma(z)$ represents the probability that the dependent variable belongs to a particular class (e.g., 1 for the event happening, 0 for the event not happening).

The coefficients $\beta_0, \beta_1, ..., \beta_n$ are estimated using maximum likelihood estimation, where the likelihood function is maximized to find the best-fitting model.

These mathematical formulations underpin the workings of linear regression and logistic regression, providing a foundation for understanding their roles and applications in machine learning.

For further insights into logistic regression, you can visit this link.

Linear Regression Vs Logistic Regression

linear regression vs logistic regression example

Aspect	Linear Regression	Logistic Regression
Type of Problem	Solves regression problems where the goal is to predict continuous outcomes.	Addresses classification tasks, aiming to predict probabilities and assign observations to discrete categories.
Output Type	Generates continuous numerical values, representing predictions directly.	Produces probabilities ranging between 0 and 1, later mapped to discrete categories based on a threshold.
Nature of Relationship	Assumes a linear relationship between input and output variables.	Models a non-linear relationship using the sigmoid function, mapping inputs to probabilities.
Evaluation Metrics	Commonly assessed using metrics such as Mean Squared Error (MSE) and R-squared.	Evaluated using metrics like accuracy, precision, recall, and F1-score to gauge classification performance.
Example Use Cases	Frequently utilized for tasks like predicting house prices, stock prices, or temperature trends.	Applied in scenarios such as spam email detection, customer churn prediction, or medical diagnosis.
Assumptions	Assumes linearity, homoscedasticity (constant variance of errors), and independence of errors.	Relies on the assumption of linearity in the log odds, independence of errors, and absence of multicollinearity.
Robustness to Outliers	Prone to the influence of outliers, which can significantly impact the model's predictions.	More robust against outliers due to the logistic function's ability to dampen their influence on the predictions.
Handling Categorical Data	Typically requires encoding techniques like dummy variables or one-hot encoding to handle categorical data.	Can handle categorical variables directly using approaches like one-hot encoding or label encoding.
Algorithm Complexity	Generally less complex and computationally efficient, making it suitable for large datasets.	More complex as it involves iterative optimization techniques, which may require more computational resources.
Implementation	Relatively straightforward to implement and understand, making it accessible to beginners.	Requires understanding of concepts like odds, log odds, and the logistic function for effective implementation.

This elaborated comparison provides a detailed insight into the differences between linear regression and logistic regression, highlighting their distinct characteristics, applications, and considerations in machine learning tasks.

FAQs

Q. When to use linear regression vs logistic regression?

A. Use linear regression when dealing with predicting continuous outcomes, such as predicting house prices. Use logistic regression for binary classification tasks, like spam email detection.

Q. Can logistic regression be used for multi-class classification?

A. Yes, logistic regression can be extended to handle multi-class classification tasks through techniques like one-vs-rest or softmax regression.

Q. Is it necessary for the relationship between variables to be linear for logistic regression?

A. No, unlike linear regression, the relationship between variables in logistic regression need not be linear. It's the relationship between the log odds of the dependent variable and the independent variables that matters.

Certainly! Here's an additional FAQ:

Q. What are some common assumptions made in linear regression and logistic regression?

A. Linear Regression assumes linearity and independence of errors. Logistic Regression assumes linearity in the log odds and the absence of multicollinearity.

Conclusion

Understanding the disparities between linear regression and logistic regression is pivotal for choosing the right algorithm for specific tasks.
Linear regression is adept at predicting continuous outcomes, whereas logistic regression shines in binary classification scenarios.
It's essential for machine learning practitioners to grasp the strengths and limitations of each algorithm to make informed decisions.
By selecting the appropriate algorithm, practitioners can effectively address various real-world challenges, whether it involves predicting house prices or identifying spam emails.
The choice of algorithm lays the groundwork for successful model development and deployment, impacting the efficacy of solutions in practical applications.