Introduction to Logarithms

What is a Logarithm?

In mathematics, the inverse of an exponential function is called the logarithmic function. In simple terms, the logarithm is the exponent or power of any number(which we call them to be the base) to which the number(which we call them to be the argument) should be raised to get another number.

We usually denote a logarithmic function as $log_ba$, where b stands for the base and a stands for argument. For example, $log_28$ is equal to the power to which the number 2 should be raised to get the number 8, and that is 3 as $2^3 = 8$, hence $log_28 = 3$ will be the answer. In general, the base of the logarithmic function must be greater than 0 b>0 and the base must not be equal to 1.

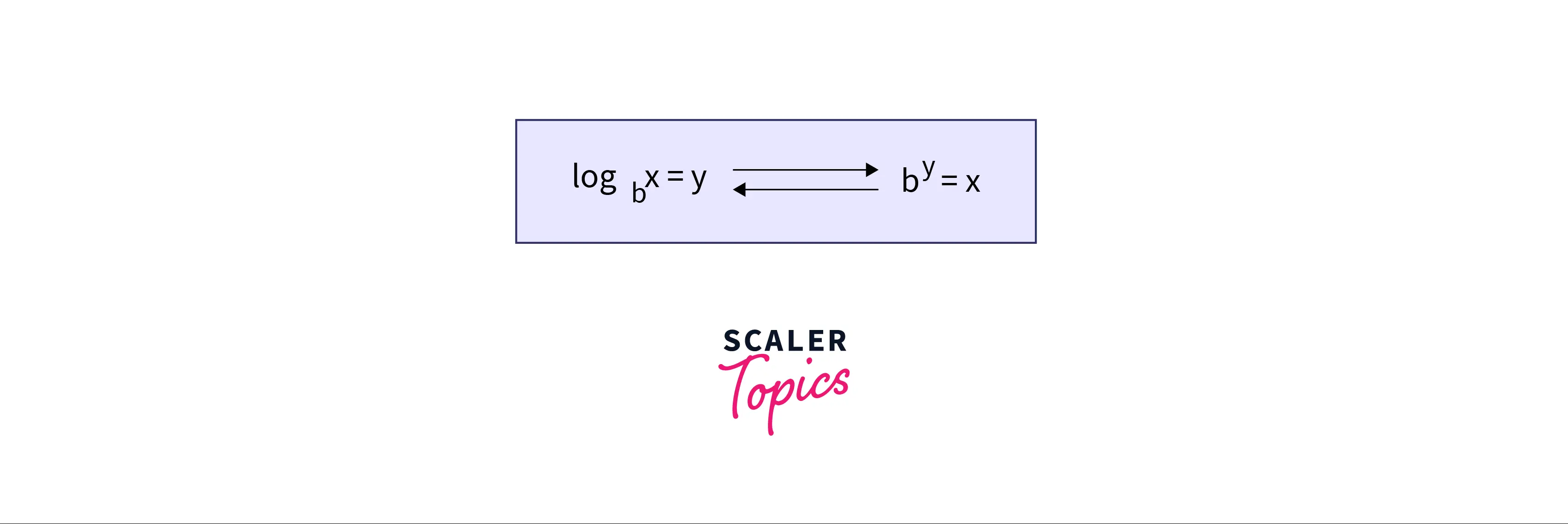
Notation

A logarithmic function's notation consists of two parts in general . They are as belows --

1. Argument
2. Base

let us discuss each of them in detail.

Argument:

In mathematics, an argument of a function is a value that must be provided to obtain that function’s result. It is also called an independent variable.

For instance, when we write 𝑠𝑖𝑛(𝑥), 𝑐𝑜𝑠(𝑥), 𝑡𝑎𝑛(𝑥) or 𝑙𝑜𝑔(𝑥), in each of these cases, 𝑥 is the argument of the problem.

Let us take $log(100)$ as an example. That number 100 in the pair of brackets is the argument of the Logarithm.

Base:

Basically, the base of any logarithmic function is the number which should be raised by any power to get the argument.

However, the logarithmic function must always have a base attached to it, for example, $log_416$ or $log_{10}1000$

The above expressions mean the following:-

• To what power should we raise 4 to get the number given as the argument, i.e. 16? The answer to that is 2
• To what power should we raise 10 in order to get the argument 1000? The answer to that is 3.

In the above example of argument, we have seen an example $log(100)$ where we did not mention the base. Many of us just write $log(100)$ out of habit, laziness, or convention. In these circumstances, the base is typically taken to be 10, because they make computations involving decimals simple. Base-10 logarithms have grown to be a crucial aspect of our lives.

The Natural Logarithm is another widely used concept of logarithms. Here, the Euler's Constant, or 2.718281828 is assumed to be the base. This number is extremely significant in mathematics, and it is frequently referred to as e.

In order to retrieve the Argument as the answer, $log_{base} argument$ only asks the following question: To what power should we raise the base to get the argument?

Types of Logarithms

There are basically two types of logarithms

• Common Logarithm
• Natural Logarithm

Let us discuss them in detail

Common Logarithm

Logarithms with a base of 10 are called common logarithms. We usually do not mention the base in case of common logarithms, for example, $log10$. Base-10 or common logarithms have become a very important part of our lives because of how it makes decimal calculations easy. Let us now have a look at how we can use this common logarithm function in Java programming language.

Syntax:

Let us look at the syntax of writing logarithms in Java programming language.

Java code :

Explanation:

• In the above syntax, we are importing the log10() function from the Java Math Library.
• The log10() method consists of an argument of double type.
• This log10() method will return the logarithm of a with a base as 10.
• Based on the argument, various cases that can occur:
• If the argument is a positive double value, then the Math.log10() method will return the logarithm of the given value with a base of 10.
• If the argument is a negative value or NaN, then the Math.log10() method will return NaN.
• If the argument is positive infinity, then the Math.log10() method will return Positive Infinity as a result.
• If the argument is positive or negative zero, then the Math.log10() method will return Negative Infinity as a result.

Natural Logarithm

Logarithms with a base of Euler’s Constant (e) or 2.718281828…… are called natural logarithms. In the case of natural logarithms, we need to mention the base as e for example $log_e10$. We mostly use this natural logarithm in mathematics and physics, to make the calculation easier and for its simpler derivative. Let us now have a look at how we can use this natural logarithm function in Java programming language.

Syntax:

Let us look at the syntax of writing logarithms in Java programming language.

Code:

Explanation:

• In the above syntax, we are importing the log() function from the Java Math Library.
• The log() method consists of an argument of double type.
• This log() method will return the logarithm of a with the base as Euler’s Constant (e).
• Based on the argument there are various cases that can occur:
  • If the argument is a positive double value, then the Math.log() method will return the logarithm of the given value with the base as Euler’s Constant (e).
  • If the argument is a negative value or NaN, then the Math.log() method will return NaN.
  • If the argument is positive infinity, then the Math.log() method will return Positive Infinity as a result.
  • If the argument is positive or negative zero, then the Math.log() method will return Negative Infinity as a result.

Logarithmic Rules and Properties

Let us now discuss different logarithmic rules and properties

Product Rule

According to the product rule, a logarithmic function of the product is equal to the sum of the logarithms of the factors. Let us look below the expression for the same --

$log_{b}(mn)$ = $log_b(m)$ + $log_b(n)$ for b > 0.

Example:

$log_2(4*8)$ = $log_2(4)$ + $log_2(8)$ = 5.
$log_{10}(10*100)$ = $log_{10}(10)$ + $log_{10}(100)$ = 3.

Division Rule

According to the Division rule, a logarithmic function of the ratio of two numbers is equal to the difference between the logarithm of the numerator to the logarithm of the denominator. Let us look below the expression for the same --

$log_b(\frac{m}{n})$ = $log_b(m)$ - $log_b(n)$ for b > 0.

Example:

$log_2(\frac{8}{4})$ = $log_2(8)$ - $log_2(4)$ = 1.
$log_{10}(\frac{1000}{10})$ = $log_{10}(1000)$ - $log_{10}(10)$ = 2.

Power rule/Exponential Rule

According to the power rule/exponential rule, the logarithm of an exponential number, or a number with power is equal to the exponent time of the logarithm of the number. Let us look below the expression for the same --

$log_b(m^n)$ = $n*log_b(m)$ for b > 0.

Example:

$log_2(8^4)$ = $4*log_2(8)$ = 12.
$log_{10}(1000^{10})$ = $10*log_{10}(1000)$ = 30.

Change of base rule

We can change the base of any logarithmic function, just by dividing the logarithm of the argument with the new base, by the logarithm of the original base with the new base. Let us look below the expression for the same --

$log_b(a)$ = $\frac{log_n(a)}{log_n(b)}$ where n = new base.

Example:

$log_2(16)$ = $\frac{log_4(16)}{log_4(2)}$ = 4.

Base Switch Rule

We can switch the base with the argument of the logarithmic function, just by taking the reciprocal or dividing with 1 of the logarithmic function. Let us look below the expression for the same --

$log_b(a) = \frac{1}{log_a(b)}$

Example:

$log_4(2)$ = $\frac{1}{log_2(4)}$ = 0.5

Derivative of log

The derivatives of any natural logarithmic function are just the reciprocal of the attribute. In the case of a logarithmic function with a base, the derivative will be reciprocal of the product of the attribute and the logarithm of the base. Let us look below the expression for the same --

$(\frac{d}{dx})log x = \frac{1}{x}$

$(\frac{d}{dx})log_b x = \frac{1}{xlog(b)}$

Example:

$(\frac{d}{dx})log x^2 = 2*\frac{d}{dx} log(x)$ = $\frac{2}{x}$

Integral of log

For the integration of natural logarithmic function, $logx$ is equal to $xlogx - x + C$, where the integration constant is C. By using the integration by parts formula (also known as the UV formula of integration) we can calculate the integral of a natural logarithmic function. Basically, the area under the curves of the function is determined by integration. Therefore, the integral of natural logarithmic function $logx$ gives the area under the curve of the function f(x) = $logx$. In mathematic terms the formula for the integration of logarithmic function $logx$ is $∫log x dx = xlogx - x + C$. Let us look below the expression for the same --

$∫log x dx = xlogx - x + C$

Additional Properties

Let us look at some additional properties of the logarithmic function.

$log_bb = 1$

If both the argument and the base of the logarithmic function are the same, then the result will be 1. As, the logarithmic function is just the inverse of exponentiation, so the base should be raised by power 1 to get the argument equal to the base($b^1 = b$ where b is base).

$log_bb = 1$

$log_b1 = 0$

If the argument is 1, no matter what is the base, the result of the logarithmic function will always be 0. As the logarithmic function is just the inverse of exponentiation, the base should be raised by power 0 to get the argument equal to 1($b^0 = 1$ where b is base).

$log_b1$ = $0$

$log_b0 = undefined$

If the argument is 0, no matter what is the base, the result of the logarithmic function will always be undefined. Because we can never get zero by raising anything to the power of the base.

$log_b0 = undefined$