Loss Functions in Neural Networks
Overview
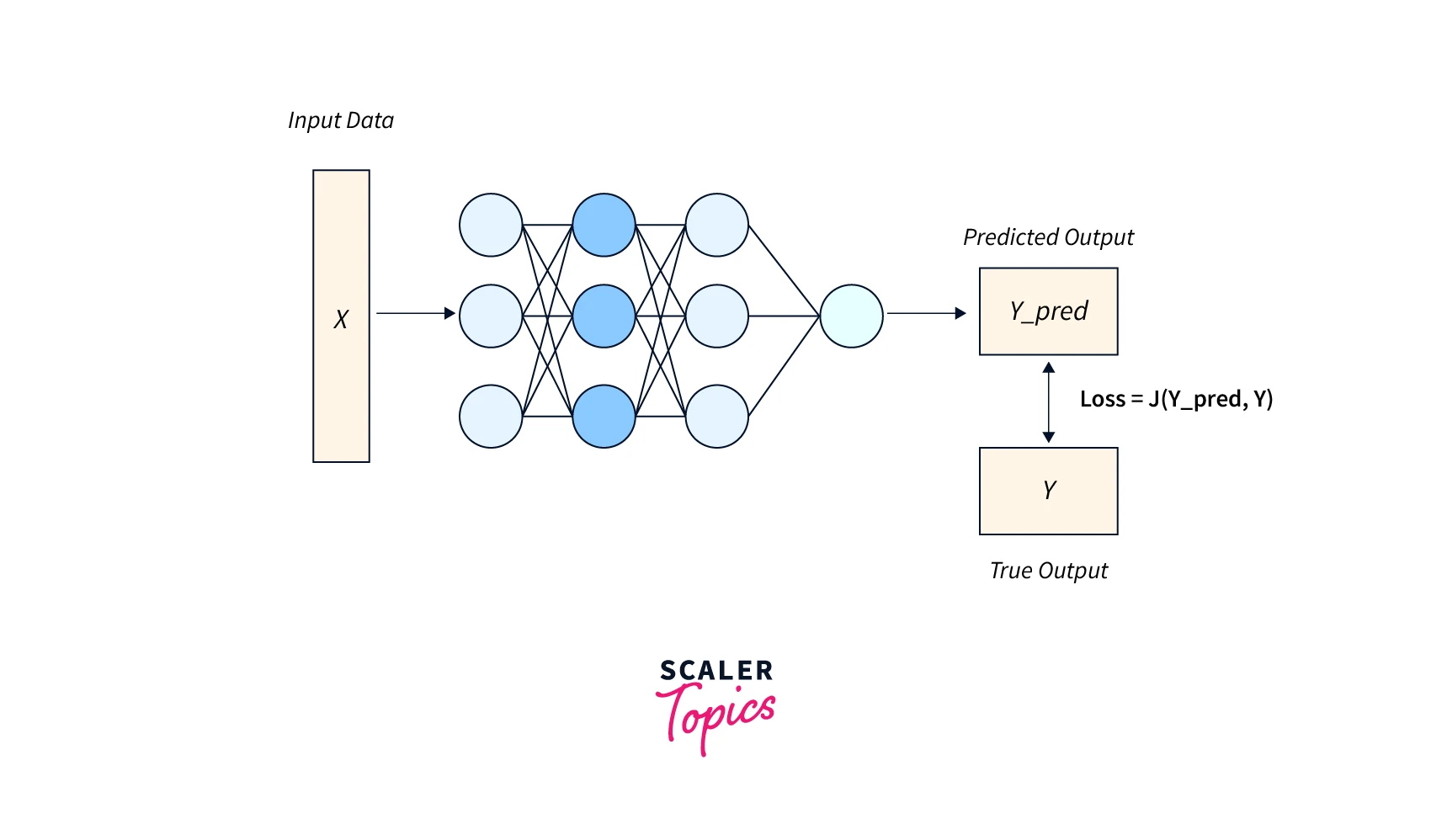
In neural networks, loss functions are used to evaluate the performance of a model and guide the optimization process. A loss function is a function that measures how well the model's predicted outputs match the true output labels. The loss function is used to optimize the model by minimizing the loss, which means the model makes fewer mistakes on the training data.
Pre-requisites
- To understand the content of this article, readers should have a basic understanding of machine learning and the concepts of prediction, optimization, and evaluation.
- Familiarity with basic mathematical operations such as sums, differences, and multiplications is also helpful.
What are Loss Functions?
A loss function is a function that measures how well a machine learning model's predicted outputs match the true output labels. The loss function is used to optimize the model by minimizing the loss, which means that the model makes fewer mistakes on the training data. The loss function is an important part of the machine learning process because it provides a way to evaluate the model's performance and guide the optimization process by indicating how the model's predictions differ from the true output labels.
Several different loss functions in neural networks exist, such as mean squared error, cross-entropy loss, and hinge loss. The choice of loss function depends on the type of task the model is being used for and the type of model being used. For example, mean squared error is often used for regression tasks, while cross-entropy loss is commonly used for classification tasks.
In addition to indicating how well the model performs, the loss function can provide insight into other aspects of the model's behavior, such as overfitting or underfitting the data. For example, if the model is overfitting the data, the loss of the training data may be very low. Still, the loss on the validation data may be high, indicating that the model needs to generalize well to unseen data.
Regression Loss Functions
Regression loss functions in neural networks measure the difference between a regression task's predicted and true values. They are used to evaluate the performance of a machine learning model in predicting a continuous value.
The choice of loss function depends on the characteristics of the task and the model being used. The goal of the model is to minimize the loss, which means that it makes fewer mistakes in the training data.
Some common loss functions in neural networks used for regression tasks include mean squared error (MSE) loss, mean squared logarithmic error (MSLE) loss, and mean absolute error (MAE) loss.
Mean Squared Error Loss
Mean squared error (MSE) loss is a common loss function used for regression tasks. It is the mean of the squared differences between predicted and true output. The MSE loss is calculated by taking the average squared difference between the predicted and true values for all the samples in the dataset. The MSE loss is used to evaluate the performance of a model on a regression task and is often used as an optimization objective when training a model.
The following equation gives the MSE loss:
Where n is the number of samples and and are the predicted and true output values, respectively.
A simple example would be a model that tries to predict the price of a house given the number of bedrooms. For a set of actual prices and predicted prices , the MSE loss would be:
The MSE loss is differentiable, meaning we can use it with gradient-based optimization algorithms. It is also a convex function with a single global minimum that optimization algorithms can find. One of the advantages of the MSE loss is that it is well-behaved and smooth, making it easier to optimize than other loss functions in neural networks. However, it is also sensitive to outliers in the data, making it less suitable for some tasks.
Mean Squared Logarithmic Error Loss
Mean squared logarithmic error (MSLE) loss is a function used for regression tasks. It is similar to mean squared error (MSE) loss, but it takes the logarithm of the predicted output before squaring the difference between the predicted and true values.
The following equation gives the MSLE loss:
Where n is the number of samples and and are the predicted and true output values, respectively.
The MSLE loss is often used when the predicted output values are expected to be positive, and the magnitude of the errors is more important than the direction (i.e., whether the prediction is higher or lower than the true value). It is differentiable and convex, making it suitable for gradient-based optimization algorithms. However, it is less well-behaved than the MSE loss and may be more difficult to optimize in some cases.
An example of using MSLE would be predicting an exponentiated target variable and, for instance, predicting the sale of a product for the next month. The true values for product sales are and predicted values .
Mean Absolute Error Loss
Mean absolute error (MAE) loss is a function used for regression tasks. It is the mean of the absolute differences between predicted and true output. The MAE loss is calculated by taking the average absolute difference between the predicted and true values for all the samples in the dataset.
The following equation gives the MAE loss:
Where n is the number of samples and and are the predicted and true output values, respectively.
The MAE loss is less sensitive to outliers in the data than mean squared error (MSE) loss, making it a suitable choice for some tasks. It is also differentiable and convex, making it suitable for gradient-based optimization algorithms. However, it is smoother than the MSE loss and may be more difficult to optimize in some cases.
For example, imagine you are training a model to predict the price of a house given its square footage. If you have four houses in your training dataset, with actual prices of and , respectively, and your model predicts prices of and , respectively, we would calculate the MAE loss as:
In this example, the MAE is , which means, on average, the model's predictions are off by .
Binary Classification Loss Functions
Binary classification loss functions in neural networks are functions that are used to evaluate the performance of a machine learning model on a binary classification task. Binary classification is a machine learning task involving predicting a binary outcome, such as a Yes/No decision or a 0/1 label.
Binary Cross-Entropy
Binary cross-entropy loss is a loss function used for binary classification tasks. It is defined as the negative log probability of the true class. It is calculated by taking the negative log of the predicted probability of the true class.
The mathematical formulation for binary cross-entropy loss is:
Where is the true label (0 or 1) and is the predicted probability of the true class (a value between 0 and 1). The binary cross-entropy loss is sensitive to the predicted probabilities and penalizes the model more for predicting low probabilities for the true class. It is often used as an optimization objective when training a model for a binary classification task.
Hinge Loss
Hinge loss is a function that trains linear classifiers, such as support vector machines (SVMs). It is the maximum difference between the predicted and true margins and a constant value. The predicted margin is the distance between the decision boundary and the closest training data point. The true margin is the distance between the decision boundary and the true label.
The following equation gives the hinge loss:
Where is the true label (-1 or 1) and is the predicted margin (a value between -1 and 1).
The hinge loss is zero when the predicted margin exceeds the true margin and increases as the predicted margin gets smaller. It is used to train linear classifiers and is similar, making it more difficult to optimize than other loss functions in neural networks.
Squared Hinge Loss
Sure! Squared hinge loss is a function that trains linear classifiers, such as support vector machines (SVMs). It is defined as the square of the difference between the predicted margin and the true margin.
The following equation gives the squared hinge loss:
Where is the true label (-1 or 1) and is the predicted margin (the distance between the decision boundary and the closest training data point).
The squared hinge loss is zero when the predicted margin exceeds the true margin ( * > 1) and increases as the predicted margin gets smaller. It is differentiable, making it suitable for gradient-based optimization algorithms.
The squared hinge loss is often used to train linear classifiers for binary classification tasks. It is less sensitive to outliers in the data than the hinge loss but is also more computationally expensive.
Multi-class Classification Loss Functions
Multi-class classification loss functions in neural networks are functions that are used to evaluate the performance of a machine learning model on a multi-class classification task. Multi-class classification is a type of machine learning task that involves predicting a class label from among multiple classes, such as predicting the type of fruit in an image from a set of classes such as "apple," "banana," and "orange."
We can use several loss functions in neural networks for multi-class classification tasks, including cross-entropy loss, softmax loss, and categorical hinge loss.
Multi-Class Cross-Entropy Loss
Multi-class cross-entropy loss is a loss function used for multi-class classification tasks, where the goal is to predict a class label from a set of K possible classes. It is defined as the negative log probability of the true class, averaged over all the samples in the dataset.
The mathematical formulation for multi-class cross-entropy loss is:
Where n is the number of samples in the dataset, is the true class label for the i-th sample, and is the predicted probability of the true class for the i-th sample.
The multi-class cross-entropy loss is calculated by taking the negative log of the predicted probability of the true class for each sample and summing the results. The loss is then averaged over all the samples in the dataset. The multi-class cross-entropy loss is sensitive to the predicted probabilities and penalizes the model more for predicting low probabilities for the true class. It is often used as an optimization objective when training a model for a multi-class classification task.
Sparse Multiclass Cross-Entropy Loss
Sparse multiclass cross-entropy loss is a loss function used for multiclass classification tasks with many classes. "Multiclass" refers to the fact that the model is trying to predict one of several possible classes, and "sparse" refers to the fact that only one class is present in each sample (as opposed to "dense," where multiple classes can be present in a single sample).
The mathematical formulation for sparse multiclass cross-entropy loss is as follows:
Where is the true label (an integer between 0 and the number of classes), and is the predicted probability for the true class (a value between 0 and 1).
The sparse multiclass cross-entropy loss is calculated by taking the negative log of the predicted probability of the true class and summing over all the samples in the dataset. It is often used as an optimization objective when training a model for a multiclass classification task with many classes.
One of the advantages of the sparse multiclass cross-entropy loss is that it is computationally efficient because it only requires predictions for the true class rather than for all the classes. However, it can be less robust to class imbalance than other loss functions in neural networks, such as dense multiclass cross-entropy loss or focal loss.
Kullback Leibler Divergence Loss
Kullback-Leibler divergence, known as KL divergence or information divergence, measures the difference between two probability distributions. Machine learning often uses it as a loss function to compare predicted and true distributions.
The following equation gives the Kullback-Leibler divergence loss:
KL Divergence Loss =
is the true probability distribution, is the predicted probability distribution.
The KL divergence loss measures the difference between the true and predicted distributions by calculating the expected value of the log of the ratio of the true distribution to the predicted distribution. It is a non-symmetric measure, which means that the KL divergence from distribution A to distribution B is not necessarily the same as the KL divergence from distribution B to distribution A.
The KL divergence loss is often used as an optimization objective when training a model to predict a probability distribution, such as in the case of generative models or models that predict the distribution of the target variable. It is a useful loss function because it allows the model to learn about the underlying structure of the data and make more informed predictions.
Writing a Custom Loss Function
Writing a custom loss function can be useful when the available loss functions in neural networks do not meet the needs of your machine-learning task or when you want to implement a new loss function for research purposes.
Here are the steps to follow when writing a custom loss function:
Step - 1:
Define the function signature: The first step is to define the function signature, which includes the function's name, the input arguments, and the return type. The input arguments should include the model's predicted output and the true output labels.
Step - 2:
Calculate the loss: The next step is calculating the loss using the predicted and true output values. This can involve applying mathematical operations such as sums, differences, and multiplications to the input values.
Step - 3:
Return the loss: The final step is to return the loss value from the function. The loss value should be a scalar value that indicates how well the model's predictions match the true output labels.
Step - 4:
Test the loss function: It is important to test the custom loss function to ensure it works as intended. We can do this by using the loss function to evaluate the performance of a model on a test dataset and comparing the results to the model's performance using a different loss function.
Here is an example of how to write a custom loss function using the Python programming language:
Output:
In this example, I tested the loss function by defining two sample arrays and passing them to the function; it returns the loss.
Remember that this is just a sample code. You can tweak the loss function and test it on the dataset as required.
Also, you need to compile the model and give your loss function as a parameter when building the model; this will tell the model to use this loss function during backpropagation.
Conclusion
- Loss functions are an important part of the machine learning process, as they are used to evaluate the performance of a model and guide the optimization process.
- There are several loss functions in neural networks, including regression loss functions, binary classification loss functions, multi-class classification loss, and Kullback-Leibler divergence loss.
- The choice of loss function depends on the type of task the model is being used for and the type of model being used.
- In some cases, it may be necessary to write a custom loss function to meet the specific needs of a task or to implement a new loss function for research purposes.
