Clustering | DBSCAN

Prerequisites

• The learner must know the basics of unsupervised learning techniques.
• Knowing the K-means algorithm in machine learning will help the learner better understand DBSCAN.
• Knowledge about mean and standard deviation will be helpful.

Introduction

Clustering analysis, or simply Clustering, is an Unsupervised learning method that divides the data points into several specific batches or groups, such that the data points in the same groups have similar properties and data points in different groups have different properties concerning specific criteria. It comprises many other methods based on differential evolution.

E.g., K-Means (distance between points), Affinity propagation (graph distance), Mean-shift (distance between points), DBSCAN (distance between nearest points), Gaussian mixtures (Mahalanobis distance to centers), Spectral clustering (graph distance), etc.

Fundamentally, all clustering methods use the same approach. First, we calculate similarities, and then we use it to cluster the data points into groups or batches. Here we will focus on the Density-based Spatial Clustering of Applications with Noise (DBSCAN) clustering method.

Clusters are dense regions in the data space, separated by regions with lower points density. The DBSCAN algorithm is based on this intuitive notion of “clusters” and “noise.” The key idea is that for each point of a cluster, the neighborhood of a given radius has to contain at least a minimum number of issues.

Why DBSCAN?

Partitioning methods (K-means, PAM clustering) and hierarchical clustering help to find spherical-shaped clusters or convex clusters. In other words, they are suitable only for compact and well-separated clusters. Moreover, they are also severely affected by the presence of noise and outliers in the data. Real-life data may contain irregularities, like:

1. Clusters such as those shown in the figure below can be of arbitrary shape.
2. Data may have noise.

The figure above shows a data set containing nonconvex clusters and outliers/noises. Given such data, a k-means algorithm has difficulties in identifying these clusters with arbitrary shapes.

The DBSCAN Algorithm:

Parameters:

The DBSCAN algorithm requires two parameters:

1. eps: This parameter defines the neighborhood around a data point. In other words, if the distance between any two points is lesser than or equal to ‘eps,’ these points are considered neighbors. If the eps value selected is too small, most data will be regarded as outliers. If it is chosen to be very large, the clusters will merge, and most data points will be in the same cluster. One way to find the eps value is based on the k-distance graph.
2. MinPts: a Minimum number of neighbors (data points) within an eps radius. The larger the dataset, the more significant value of MinPts must be chosen. As a general rule, the minimum MinPts can be derived from the number of dimensions D in the dataset as $MinPts >= D+1$. The minimum value of MinPts must be chosen to be at least 3.

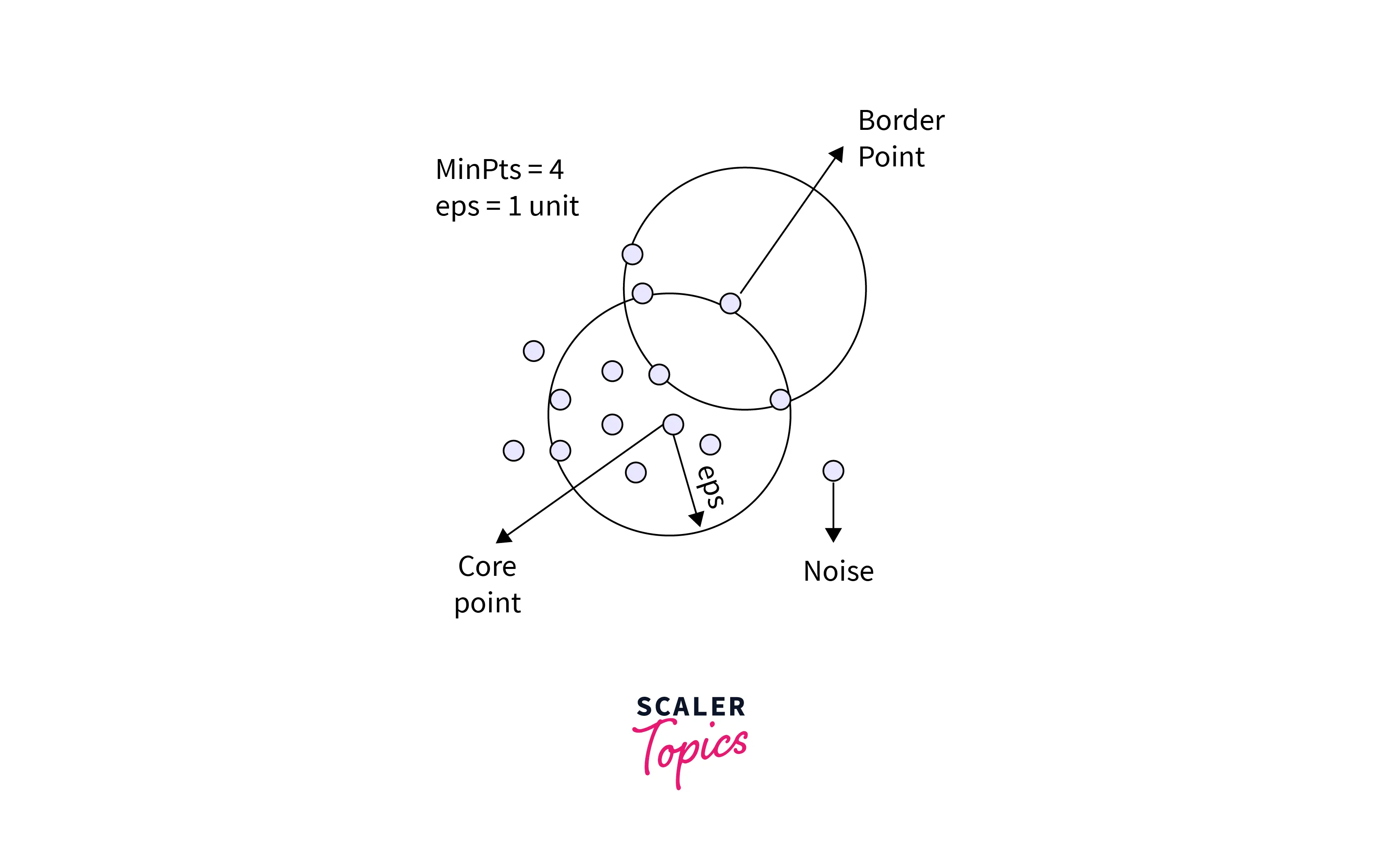
In this algorithm, we have three types of data points:

1. Core Point: A point is a core point if it has more than MinPts points within eps.
2. Border Point: A point with fewer than MinPts within eps but is in the neighborhood of a core point.
3. Noise or outlier: A point that is not a core or border point.

The Algorithm

The DBSCAN algorithm can be summarized in the following four steps. These are:

1. Find all the neighbor points within eps and identify the core points or visited with more than MinPts neighbors.
2. If it is not already assigned to a cluster, create a new one for each core point.
3. Find all its density-connected points recursively and assign them to the same cluster as the core point. Points a and b are density connected if point c has a sufficient number of points in its neighbors and points a and b are within the eps distance. This is a chaining process. So, if b is a neighbor of c, c is a neighbor of d, and d is a neighbor of e, which in turn is a neighbor of a, implying that b is a neighbor of a.
4. Iterate through the remaining unvisited points in the dataset. Those points that do not belong to any cluster are noise.

Pseudocode

Evaluation Metrics

• Silhouette score : Silhouette's score is in the range of -1 to 1. A score near 1 denotes the best, meaning that the data point i is very compact within the cluster to which it belongs and far away from the other clusters. The worst value is -1. Values near 0 denote overlapping clusters.
• Absolute Rand Score : Absolute Rand Score is in the range of 0 to 1. More than 0.9 denotes excellent cluster recovery, and above 0.8 is a good recovery. Less than 0.5 is considered to be poor recovery.

Code Example in Python

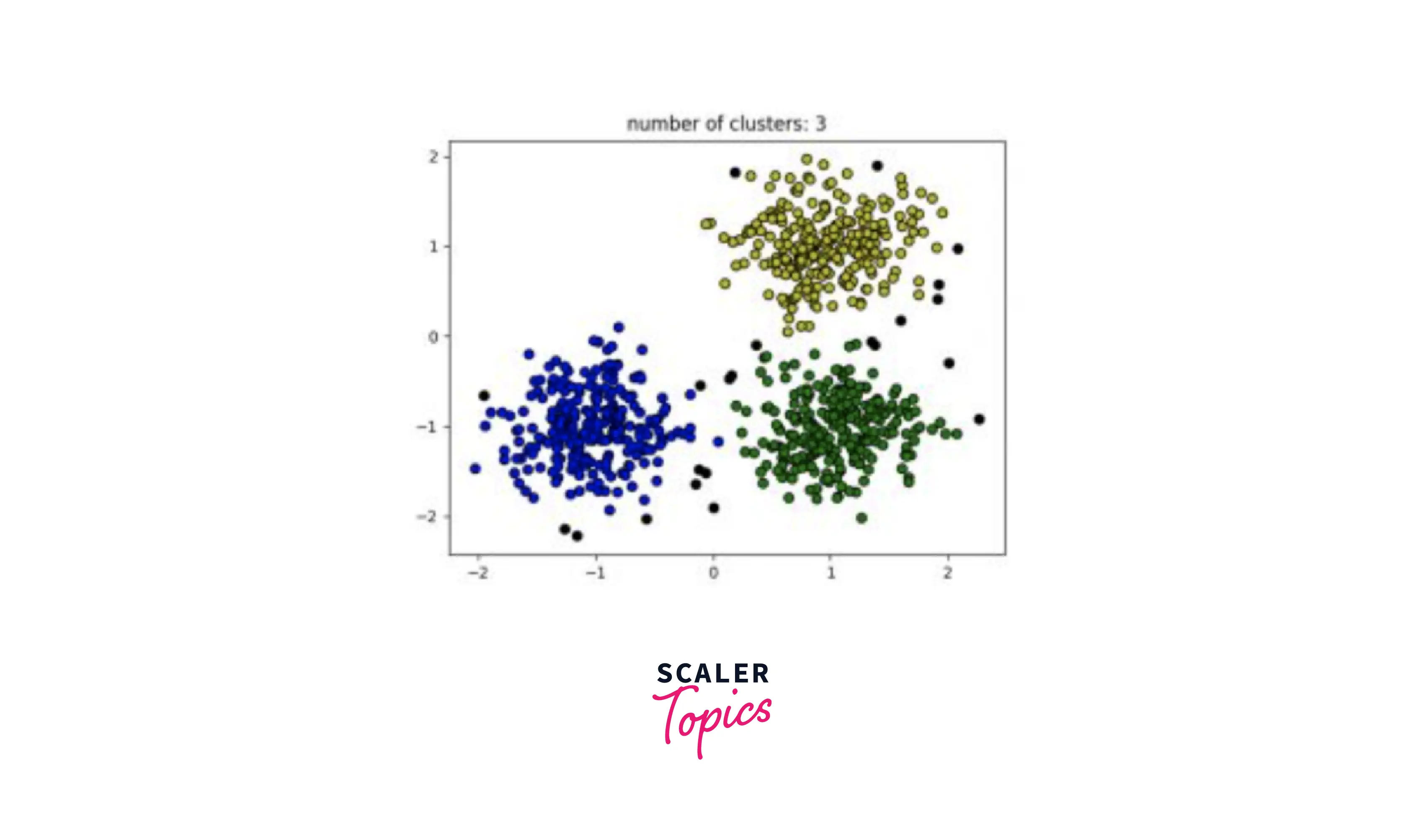
In this snippet, we have used the DBSCAN module from sklear.cluster library. Using the make_blobs function, we have created our own dataset consisting of random points. After removing all the noise from our dataset, we use a loop to plot all of our clusters. To conclude, we use Matplotlib to display our clusters.

The output of the above code is shown below: