Types of Errors in Machine Learning

Prerequisites

Before this article, you must know a bit about:

• Basic probability concepts.
• The lifecycle of a Machine Learning project.

Introduction

As we discussed earlier in this article, calculating errors in our Machine Learning models helps us understand our model's less-impacting areas and various ways to tackle them. Amongst the uses of errors in Machine Learning, it is also used quite a lot when comparing various Machine Learning algorithms for a problem statement. With the help of errors, we can determine which model has the highest accuracy.

Error calculation is the process of isolating, observing, and diagnosing various ML predictions, thereby helping understand the highs and lows of the model. This article will unravel various methods to calculate and minimize errors.

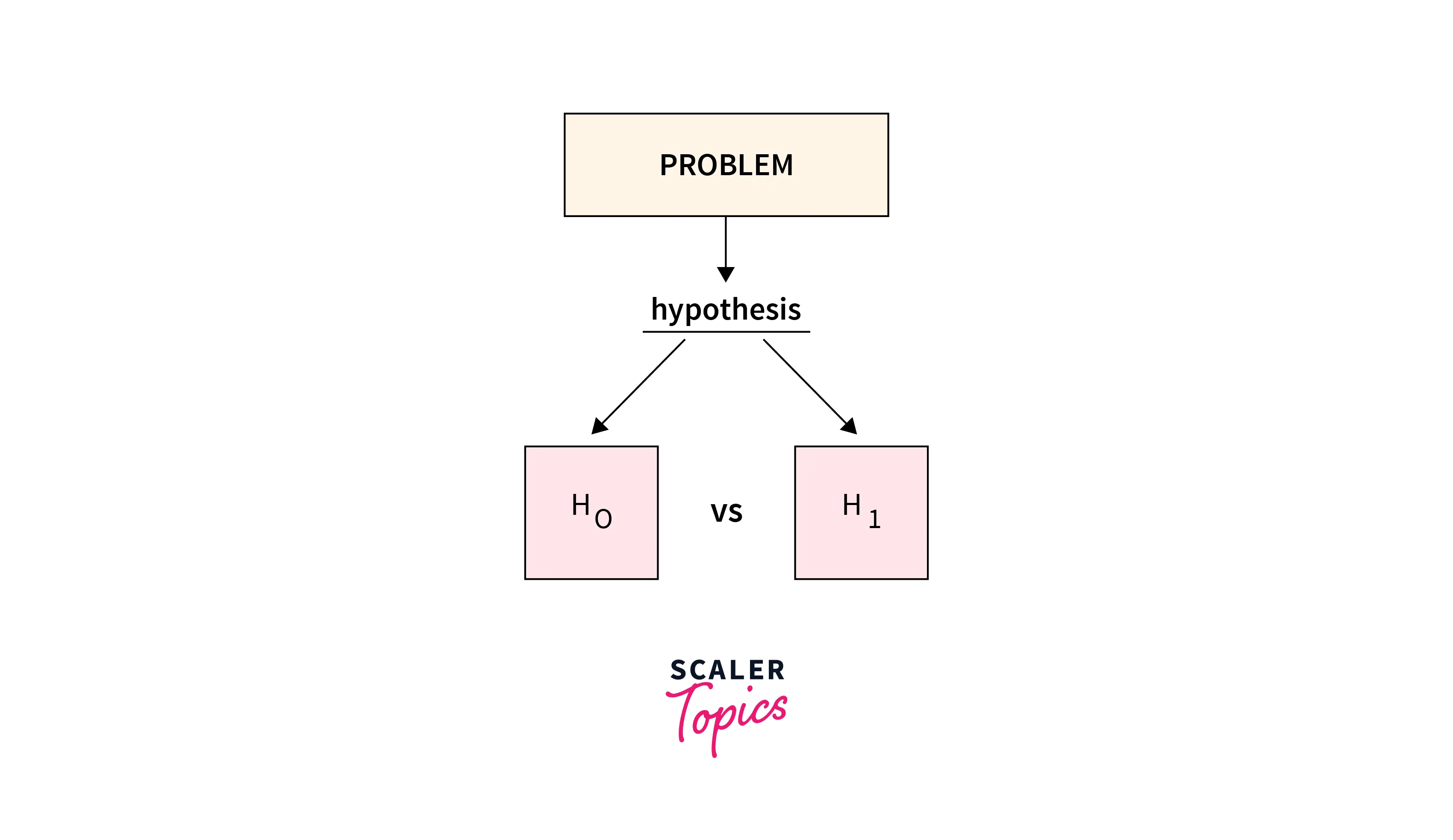
Importance of Hypothesis

Hypothesis (Hypothesis Testing, to be precise) is an idea generated from an educated guess. We basically take a statement (should be falsifiable) and then try to prove its authenticity. If the educated assumption holds, then the hypothesis is considered true, else it's not held in contention.

Using statistical hypothesis, we calculate a critical effect; this effect determines if our observed assumption holds true or not. In practice, we generate a null hypothesis(H0), in which there is no difference between population means based on samples. Then, we use the statistical/alternate hypothesis (H1) to challenge the null hypothesis, to either accept or deny the hypothesis.

Probability and P-Values

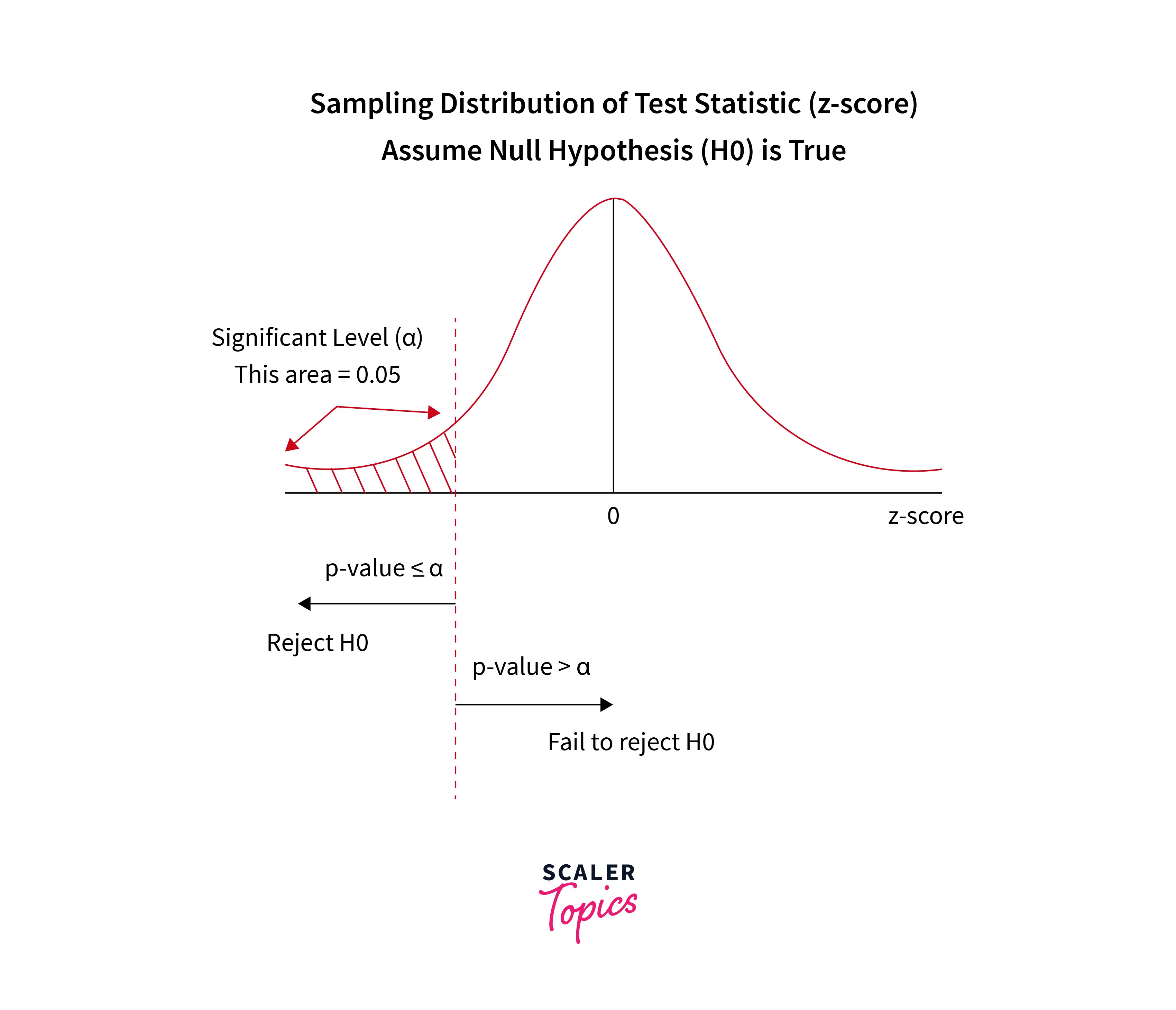
Probability can be described as the foundation of Machine Learning. Most of the Machine Learning models run on probability. Probability measures the level of certainty associated with an ambiguous event. In hypothesis testing, the probability is also known as P-Value, and it lies between 0 and 1. The P-value in Hypothesis Testing signifies whether the statistical hypothesis (H1) is true. This means that the lesser the P value, the better the chances for the null hypothesis to be true.

This threshold for P-Value is known as the Level of Significance. The main condition regarding the Level of Significance is:

If the p-value is equal to or less than 0.05 (depending on the use case), then the result can be called significant.

The P value is the probability that the observed results would occur if the null hypothesis were true. So a p-value less than 0.05 means that the observed results would occur less than five out of a hundred times if the null hypothesis is true. Hence, we must reject the null hypothesis. However, if the p-value is greater than 0.05, the null hypothesis is not rejected because the deviation from it is not statistically significant.

Error Measurement in Classification Problems

Now that we have covered what errors are in Machine Learning and how they influence the accuracy of our model, let us dive deep into the various types of error measurement metrics used in Machine Learning.

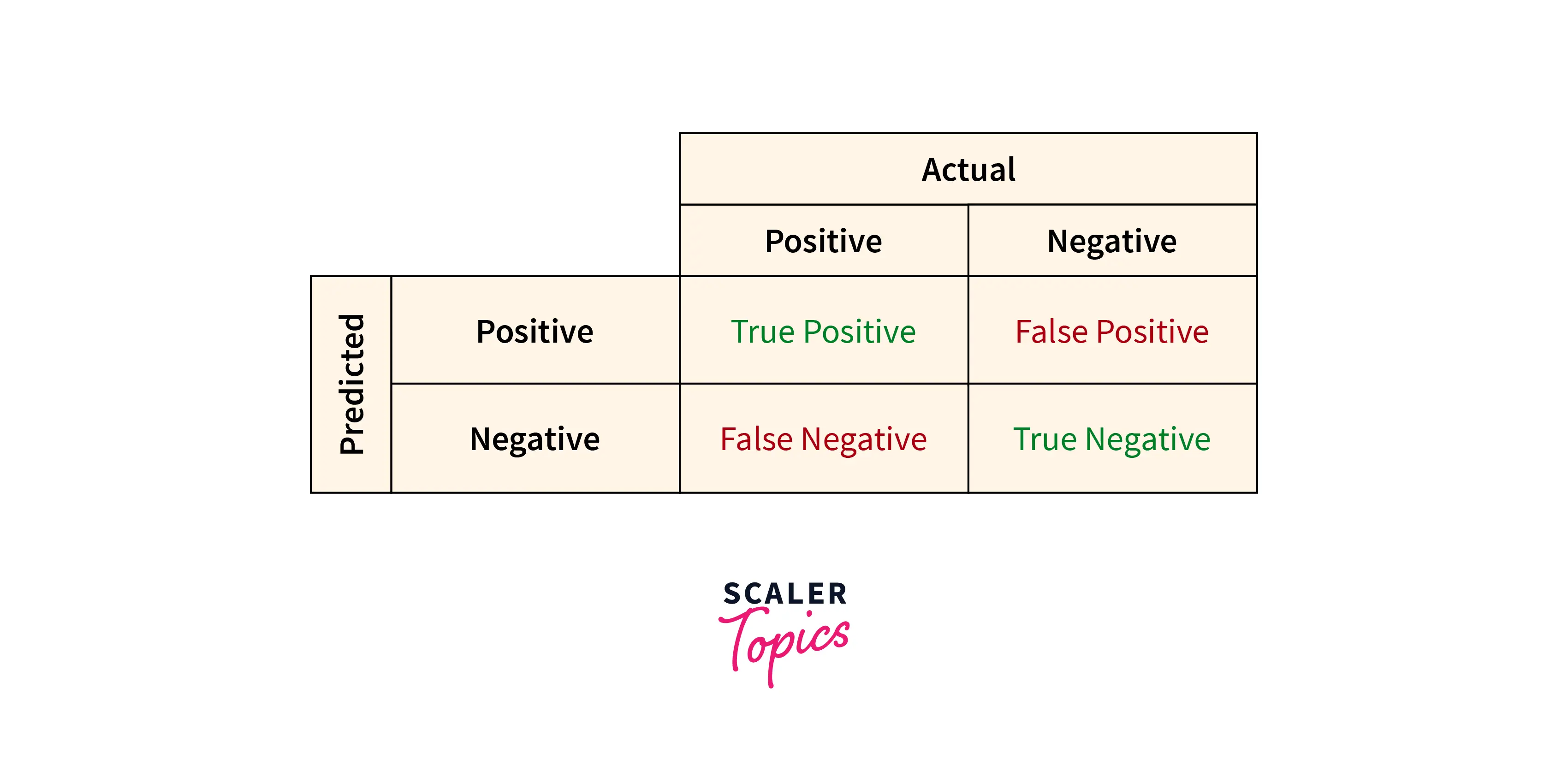
Error Measurements are mostly used in binary classification problems (determining if a certain observation is right or not). There are four types of error measurement methods in classification problems:

• True Positive (TP) When the observation from the dataset is true, and the value calculated using our model comes out to be true, we have a true positive scenario.
• False Positive (FP) In the False Positive error, the value in the dataset is true, while the computed value appears to be false. It is also known as Type I error.
• False Negative (NP) A false negative error is one where the computed value is false while the value in the dataset is true. It is also called Type II error.
• True Negative (TN) Similar to True Positive, True Negative happens when the value computed is the same as the value in the dataset, the value being false.

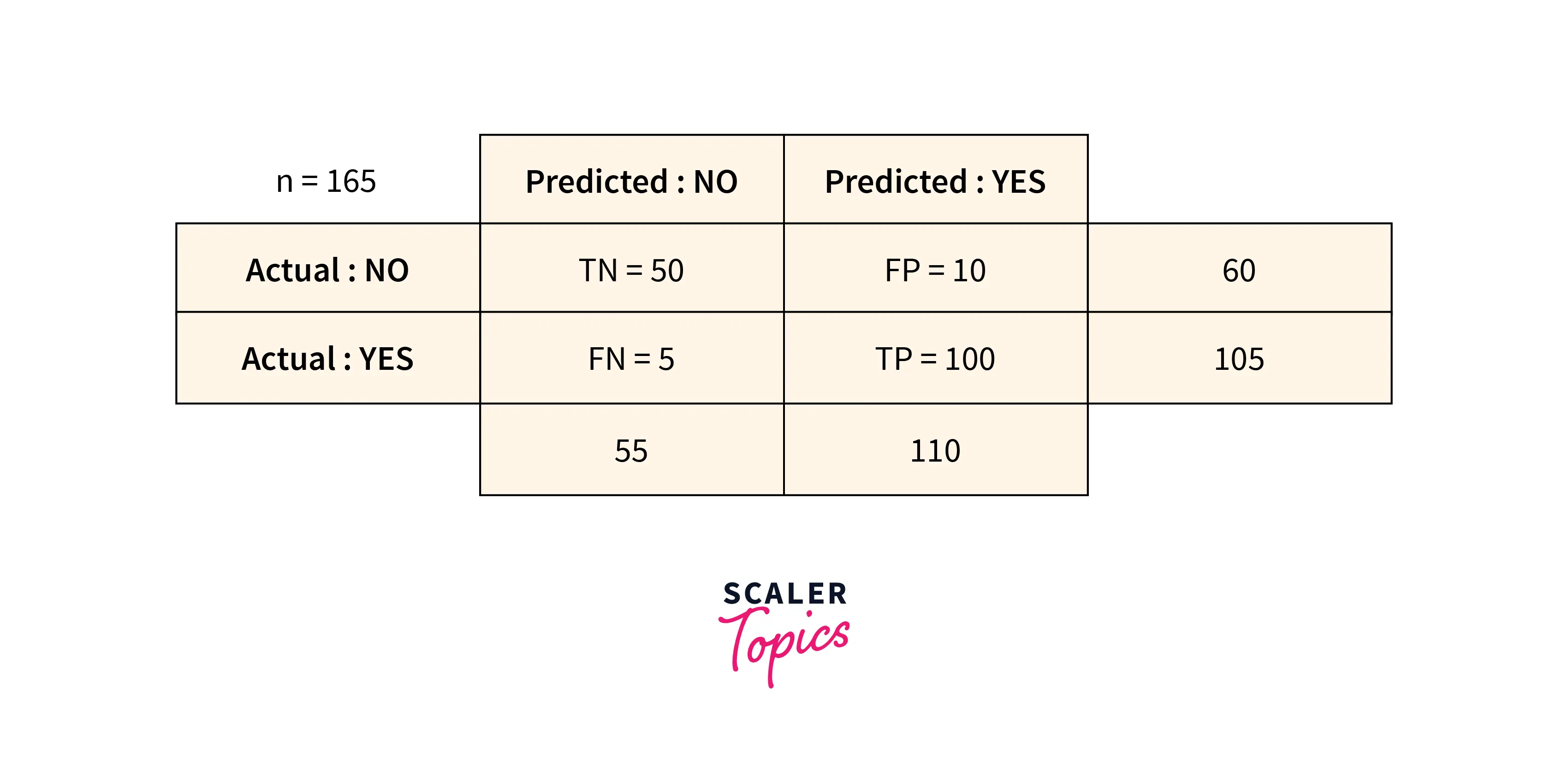
Confusion Matrix

An additional method to measure errors in the Machine Learning model is a Confusion Matrix. It is an upgrade over the methods discussed earlier in this article; it computes metrics like recall, precision, specificity, accuracy, and ROC scores.

• Recall Recall, also known as sensitivity, is the proportion of correctly predicted positive observations to all of the actual class's observations. $Recall = True Positives/(True Positives + False Negatives)$

• Precision The proportion of accurately anticipated positive observations to all predicted positive observations is known as precision. $Precision = True Positives/(True Positives + False Positives)$

• Accuracy Accuracy, the proportion of properly predicted observations to all observations, is the most used performance metric. $Accuracy = (Observed Value - Actual Value)/Actual Value * 100$

• ROC Score The ROC (Reciever Operating Characteristic) score is the slope of a ROC plot, which shows the performance of a classification model at all classification thresholds. The two parameters for the ROC score are True Positive Rate and False Positive Rate