Classification Models | F-Β Score

Pre-requisites

Before going further in this article, the reader must be familiar with the basics of classification metrics, such as:

• Precision: Percentage of positive predictions that belong to the positive class.
• Recall: Percentage of all the positive class samples in the dataset that are predicted correctly.

Introduction

As we discussed earlier in this article, error calculation metrics are very important when it comes to Classification Problems in Machine Learning because they improve the performance of our models by providing insight into how well they are able to classify the data. The main aim of Machine Learning models is to take note of the metrics and further improve themselves.

Python supplies many categorization metrics to assist us in determining the ideal setups for our machine-learning models to serve this function. In this article, we will unravel F-1 and F-beta scores, their importance, and how they are implemented to get the best out of any classification Machine Learning model.

The F-1 Score

The F-1 Score is a very popular choice amongst Machine Learning developers, as it uses the two most reliable sources of accuracy; precision and recall.

$F1 score = (2*Precision*Recall)/Precision + Recall$

As discussed earlier, the F1 score is made up of two variables:

• Precision Percentage of positive predictions that belong to the positive class.

$Precision = True Positives/(True Positives + False Positives)$

• Recall Percentage of all the positive class samples in the dataset that are predicted correctly.

$Recall = True Positives/(True Positives + False Negatives)$

Now that we have learned about the F-1 score, let us dive into the much-generalized version of the F-1 Score; F-beta score.

The F-β Score

The F-beta score is a step up to the F-1 score, as it enables us to choose how to balance precision and recall using the beta parameter. The beta (β) represents the harmonic mean between precision and recall.

$F-β Score = ((1+beta^2)*Precision*Recall)/beta^2*Precision+Recall$

As we can see, the beta variable is very influential. If the beta value is 1, then the F-β score will be equal to the F-1 score. If the beta is 0.5, then the F-β would be slightly more than the F-1 score.

Imbalanced Classification and F-β Scores

When working with F-1 and F-β scores, we might expect an anomaly sometimes. As we know, F-β score is supposed to be an upgrade over F-1 score, but it is not the case in certain scenarios. Let us understand this in-depth using an example.

For illustration, let us take the Titanic Dataset. We will create our Machine Learning model using Logistic Regression. Since the problem statement asks us to predict one dependent variable, Logistic Regression would be a wise choice.

In the code above, we use NumPy to create linearly spaced elements, and with the help of these elements, we create various probability thresholds. These thresholds will help us to plot various probabilities regarding the different scores.

Output

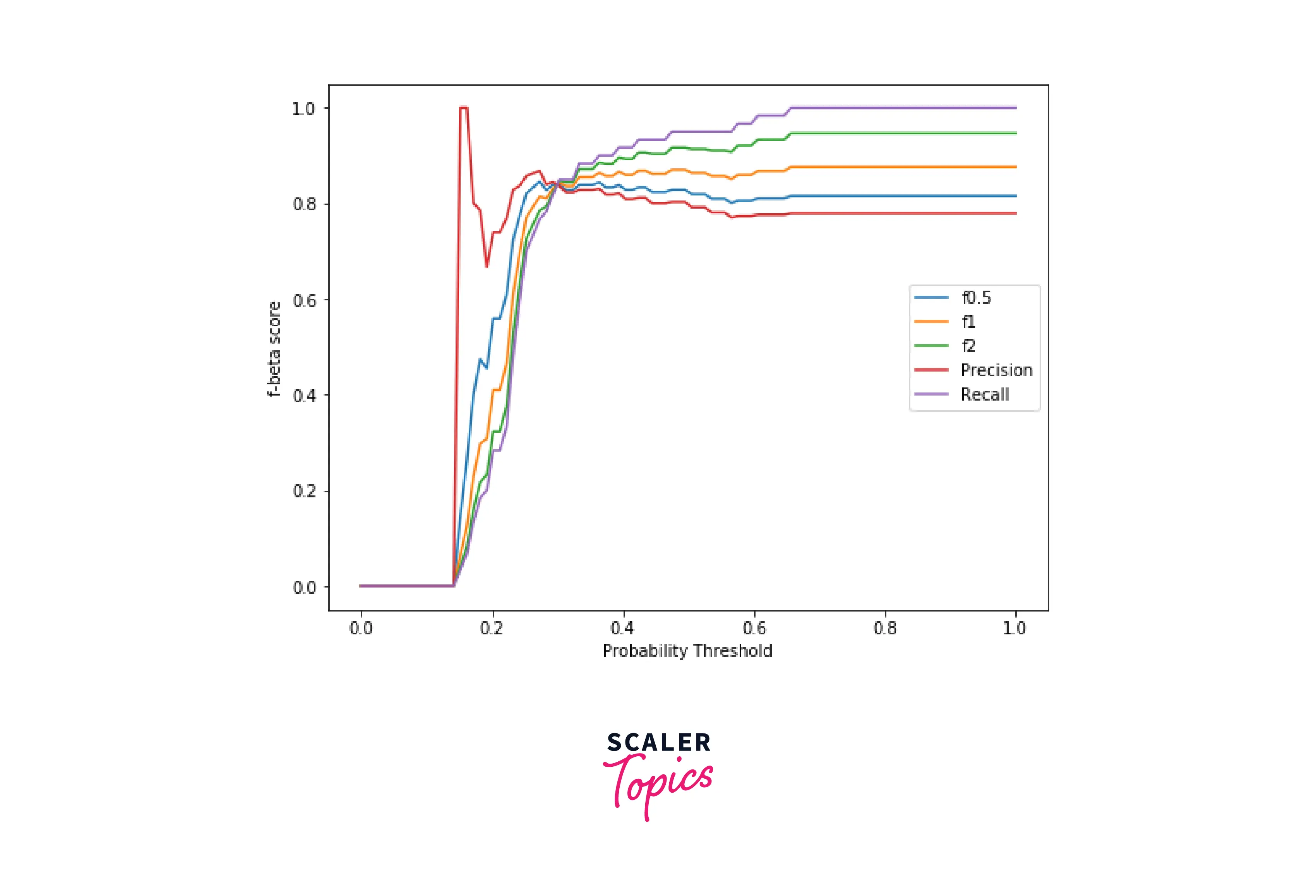
As we can see, recall is the metric with the highest f-beta score and precision is the metric with the lowest f-beta score. Although the F0.5, F1, and F2 curves are quite similar in shape, they have different values. Hence, the question arises; How can we choose the beta value to get better results?

If we want to prioritize minimizing false positives over reducing false negatives, we must select a beta value less than 1, since precision would have more influence over recall. When precision has more influence, the model will be more selective in making a positive prediction, minimizing false positives.

Conversely, to minimize false negatives rather than minimizing false positives, we must select the beta value to be more than 1. In this case, recall would be given more importance than precision. Hence the model tries to get as many positive samples as it can and, in doing so, minimizes false negatives.

Applying the concepts we learned above, we can safely say that amongst the F scores, F2 would be a great choice for the Titanic Dataset.

Code Implementation

In this section, we will calculate the F-beta score using Python. The Machine Learning algorithm that we will use is the DecisionTree classifier. The Decision Tree classifier is an optimal choice when working with smaller datasets. Learn more about Decision Tree classifiers here (insert link).

Output