What are Linear Models in Machine Learning?
Overview
The Linear Model is one of the most straightforward models in machine learning. It is the building block for many complex machine learning algorithms, including deep neural networks. Linear models predict the target variable using a linear function of the input features. In this article, we will cover two crucial linear models in machine learning: linear regression and logistic regression. Linear regression is used for regression tasks, whereas logistic regression is a classification algorithm. We will also discuss some examples of the linear model, which has essential applications in the industry.
Introduction to Linear Models
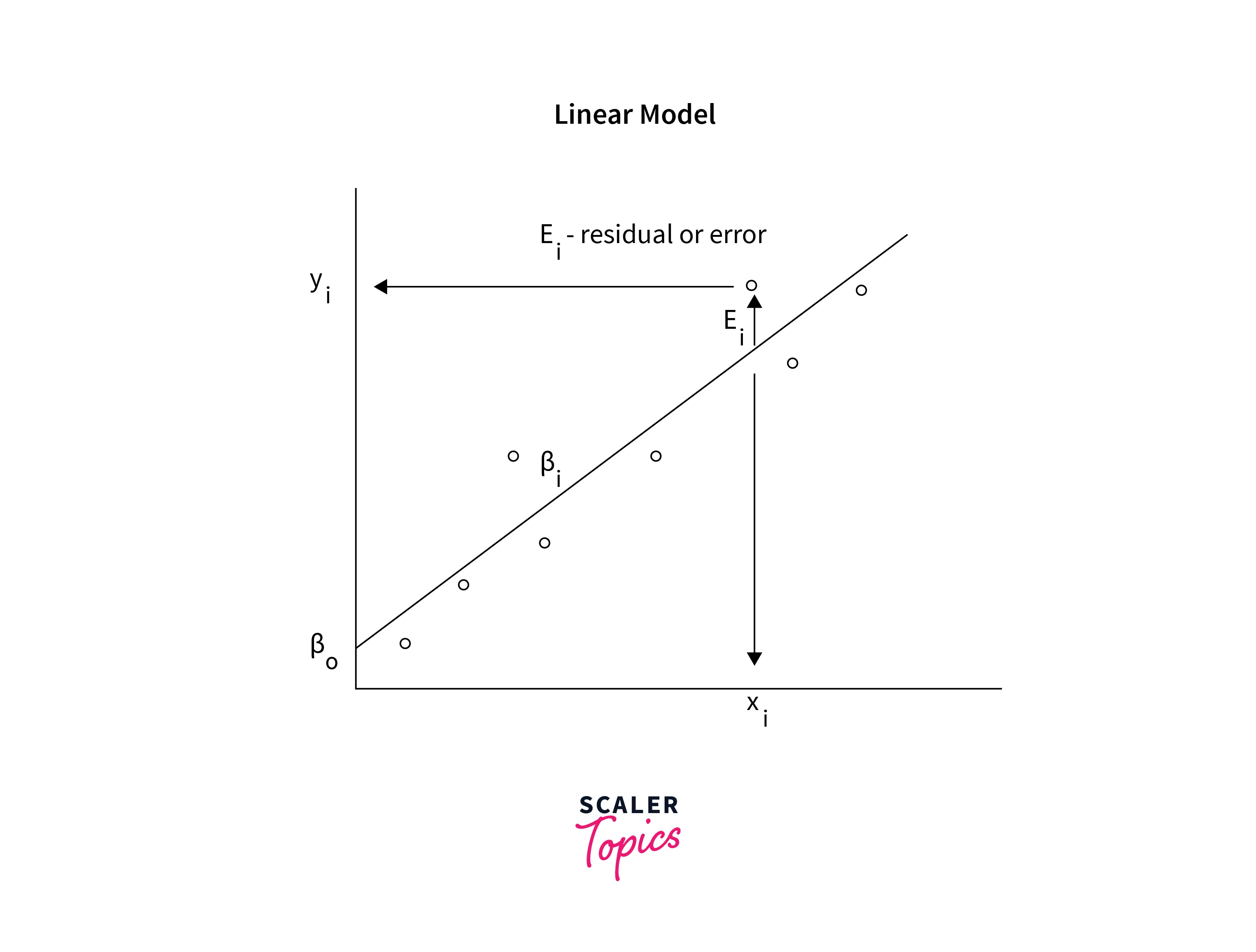
The linear model is one of the most simple models in machine learning. It assumes that the data is linearly separable and tries to learn the weight of each feature. Mathematically, it can be written as , where X is the feature matrix, Y is the target variable, and W is the learned weight vector. We apply a transformation function or a threshold for the classification problem to convert the continuous-valued variable Y into a discrete category. Here we will briefly learn linear and logistic regression, which are the regression and classification task models, respectively.
Linear models in machine learning are easy to implement and interpret and are helpful in solving many real-life use cases.
Types of Linear Models
Among many linear models, this article will cover linear regression and logistic regression.
Linear Regression
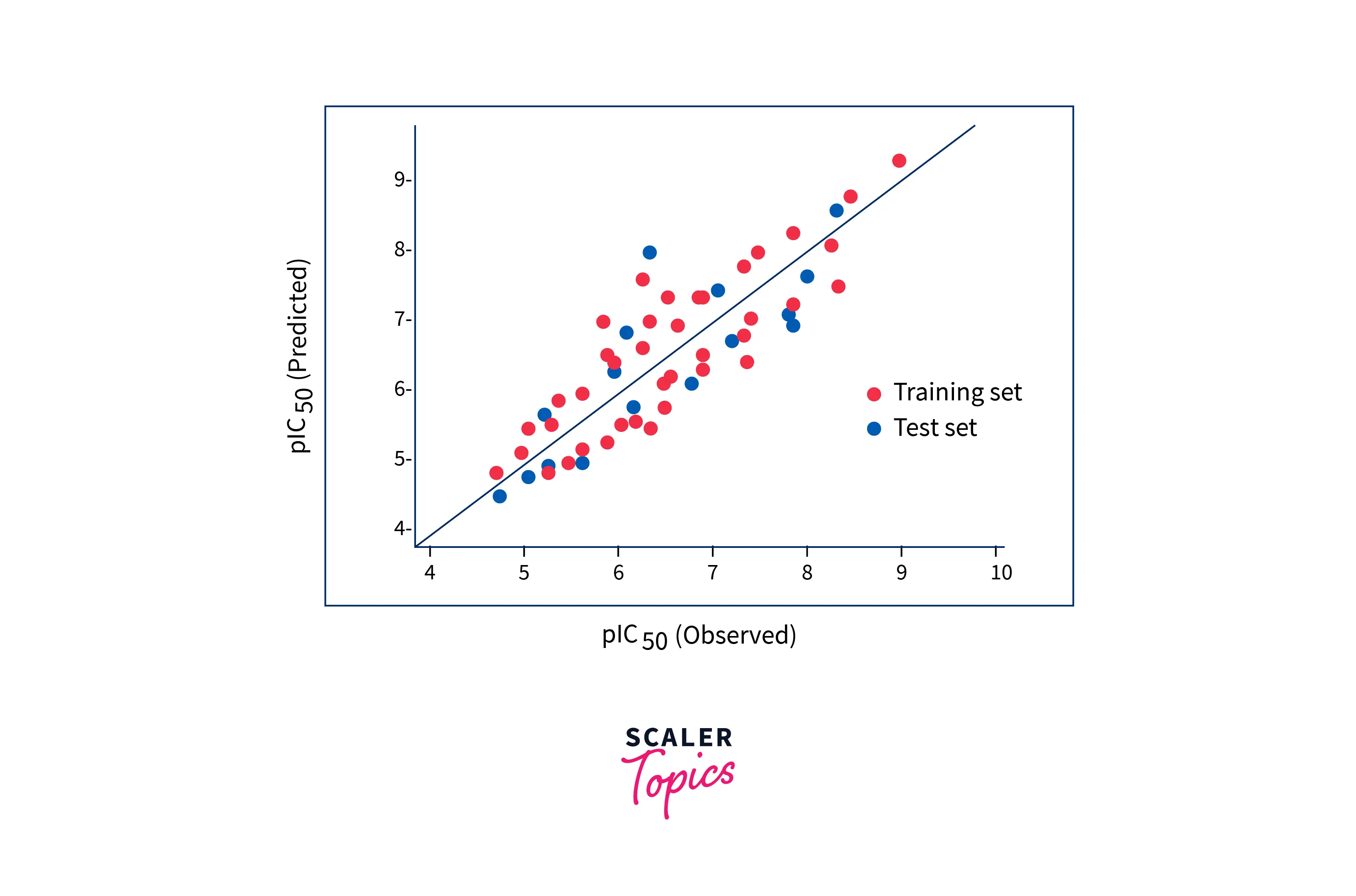
Linear Regression is a statistical approach that predicts the result of a response variable by combining numerous influencing factors. It attempts to represent the linear connection between features (independent variables) and the target (dependent variables). The cost function enables us to find the best possible values for the model parameters. A detailed discussion on linear regression is presented in a different article.
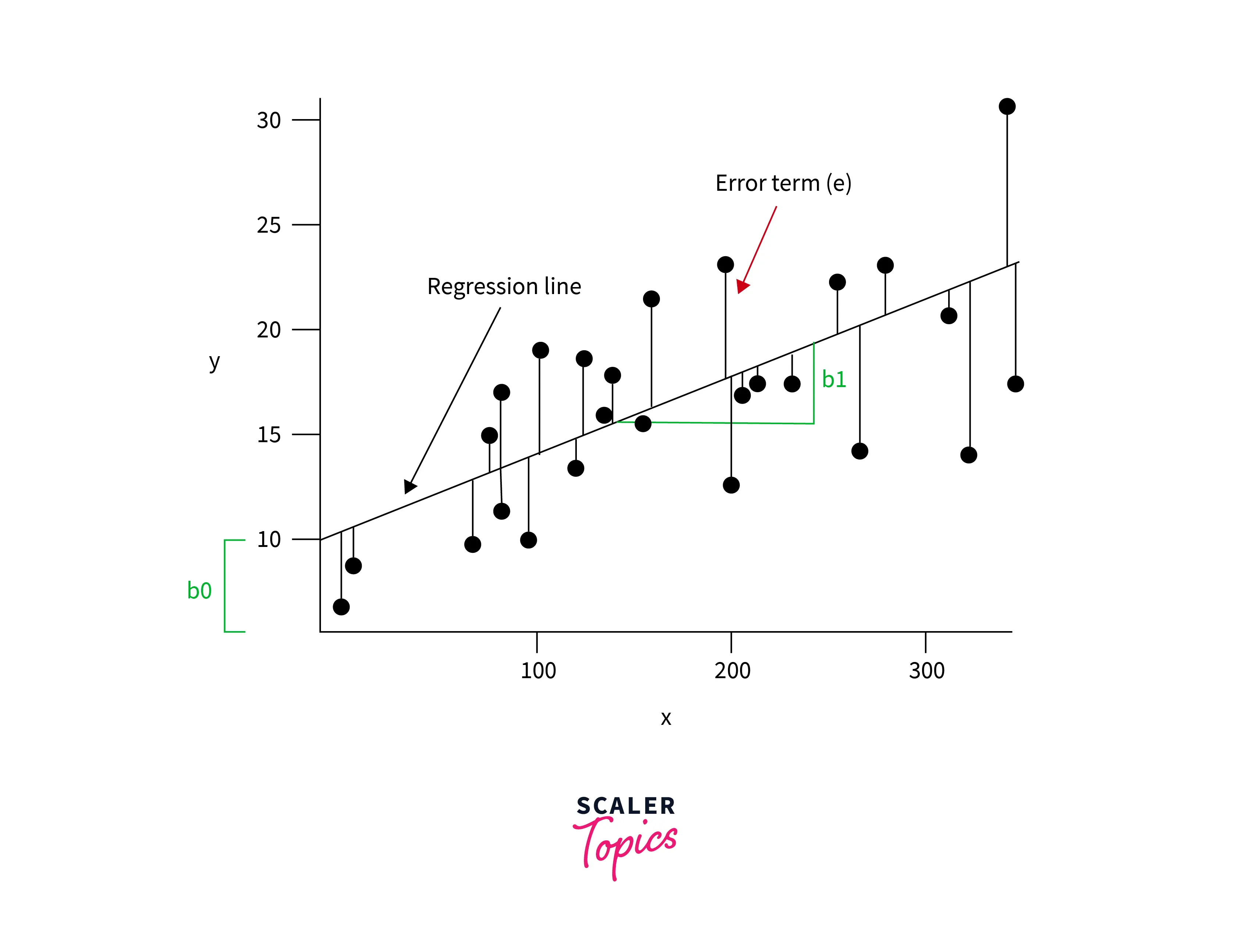
Example: An analyst would be interested in seeing how market movement influences the price of ExxonMobil (XOM). The value of the S&P 500 index will be the independent variable, or predictor, in this example, while the price of XOM will be the dependent variable. In reality, various elements influence an event's result. Hence, we usually have many independent features.
Logistic Regression
Logistic regression is an extension of linear regression. The sigmoid function first transforms the linear regression output between 0 and 1. After that, a predefined threshold helps to determine the probability of the output values. The values higher than the threshold value tend towards having a probability of 1, whereas values lower than the threshold value tend towards having a probability of 0. A separate article dives deeper into the mathematics behind the Logistic Regression Model.
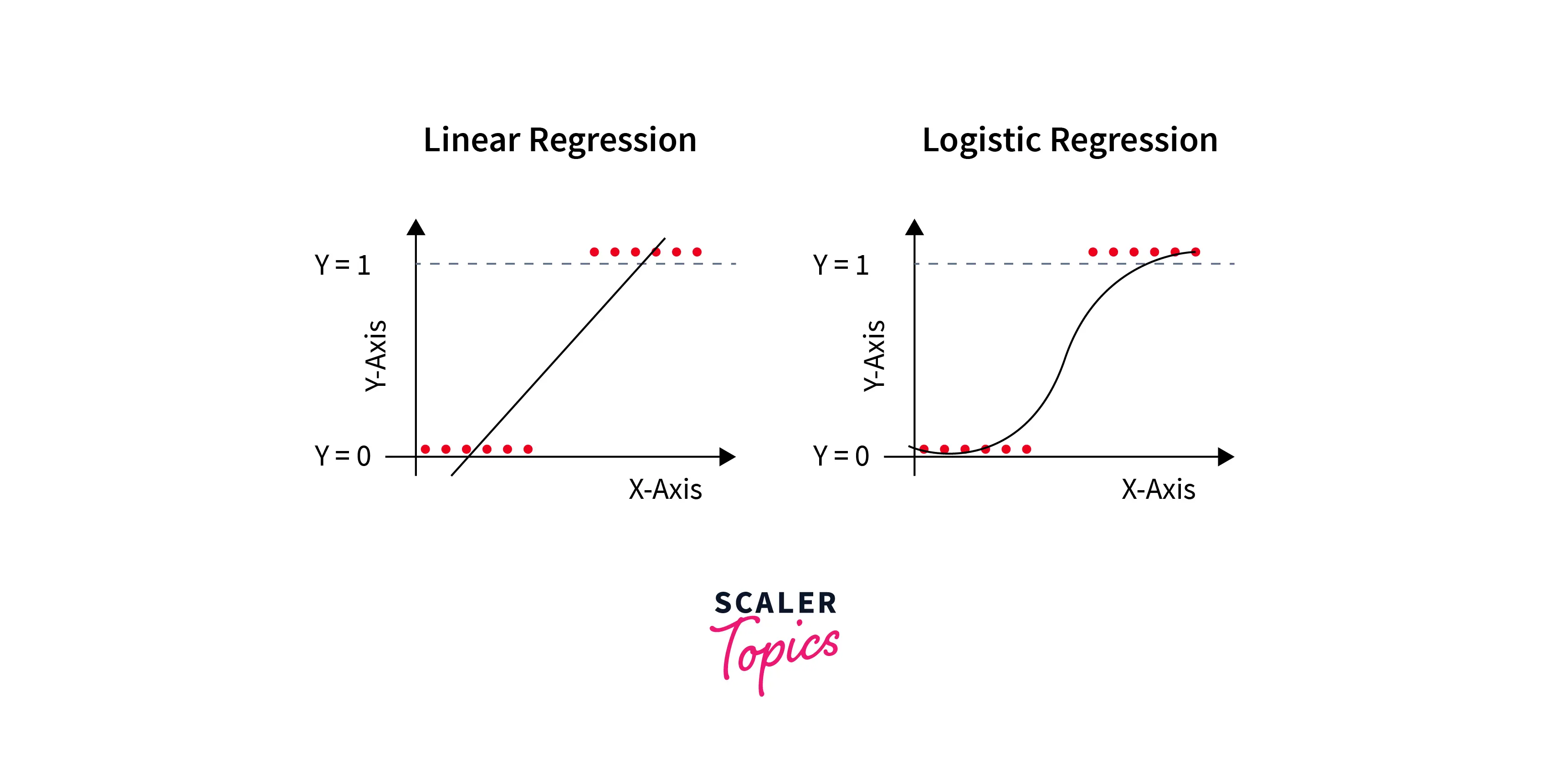
Example: A bank wants to predict if a customer will default on their loan based on their credit score and income. The independent variables would be credit score and income, while the dependent variable would be whether the customer defaults (1) or not (0).
Applications of Linear Models
Several real-life scenarios follow linear relations between dependent and independent variables. Some of the examples are:
- The relationship between the boiling point of water and change in altitude.
- The relationship between spending on advertising and the revenue of an organization.
- The relationship between the amount of fertilizer used and crop yields.
- Performance of athletes and their training regimen.
Conclusion
- In this article, we have covered linear models in machine learning.
- Linear and logistic regression were also discussed in brief here.
- Some real-life applications of linear models are also presented here.
- A detailed discussion on linear and logistic regression will be presented in a subsequent article.
