Support Vector Machine in Machine Learning

Overview

Support Vector Machine, or SVM, is one of the most popular Supervised Learning algorithms used for Classification, Regression, and anomaly detection problems. However, this article covers how SVM is used for classification purposes. The same can be easily extended for regression and anomaly detection tasks. The SVM algorithm works by creating the best line or decision boundary that can classify new data points in the correct category in the future. In this article, we will cover Linear Support Vector Machines. It can work as a nonlinear classifier with the help of a kernel trick, which will be covered later.

Prerequisites

Learners must know the basics of machine learning, specifically what is supervised machine learning.
Knowledge about linear algebra is mandatory.
Knowledge of gradient descent and calculus is also required to understand the article better.

What is Support Vector Machine?

SVM is a supervised machine learning algorithm that classifies data from two or more different classes. SVMs differ from other classification algorithms because they choose the decision boundary that maximizes the distance from all the classes' nearest data points. The decision boundary created by SVMs is called the maximum margin hyperplane, and SVM is called the Maximum margin classifier.

Hyperplane and Support Vectors in SVM

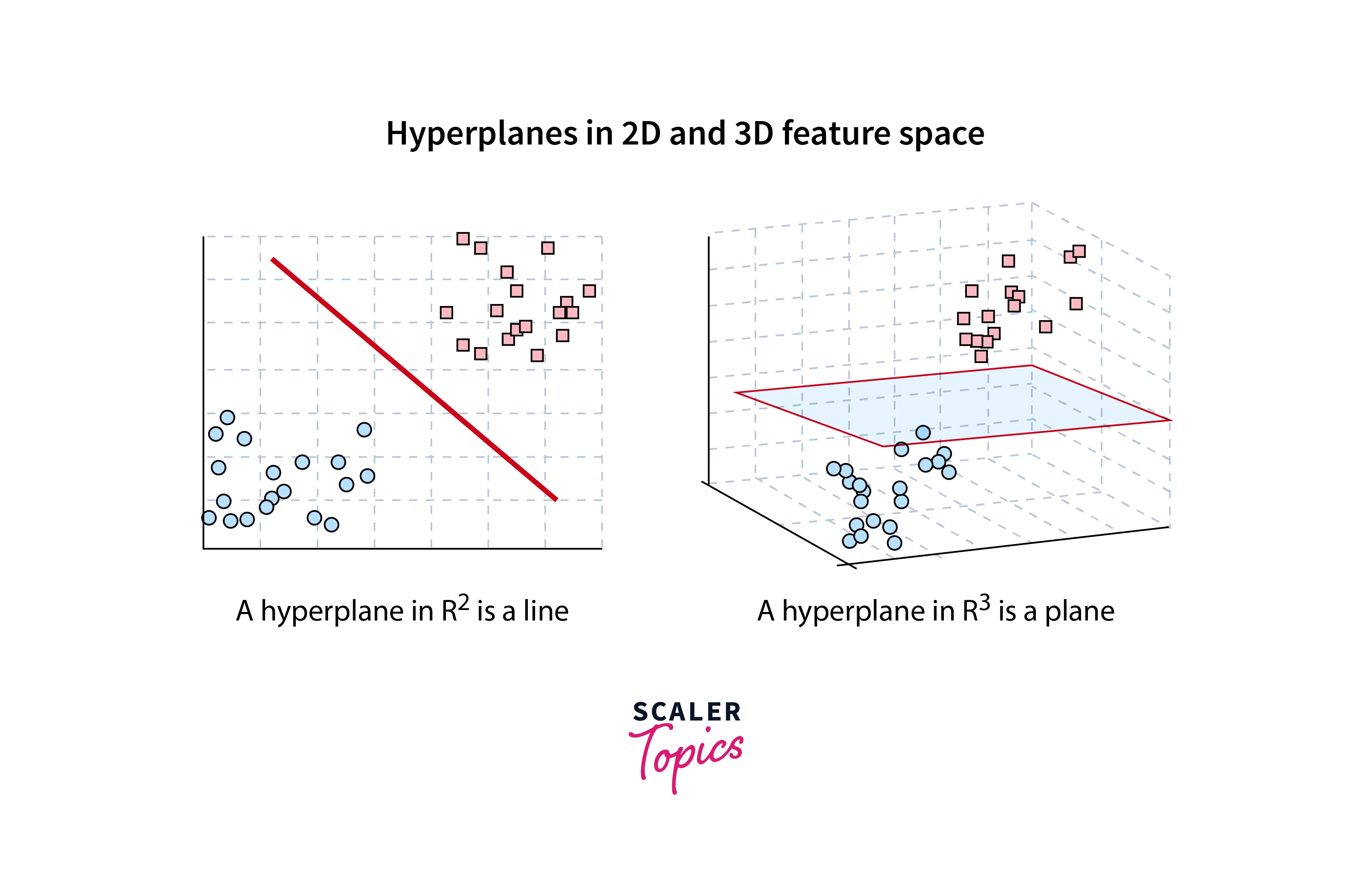
Hyperplane

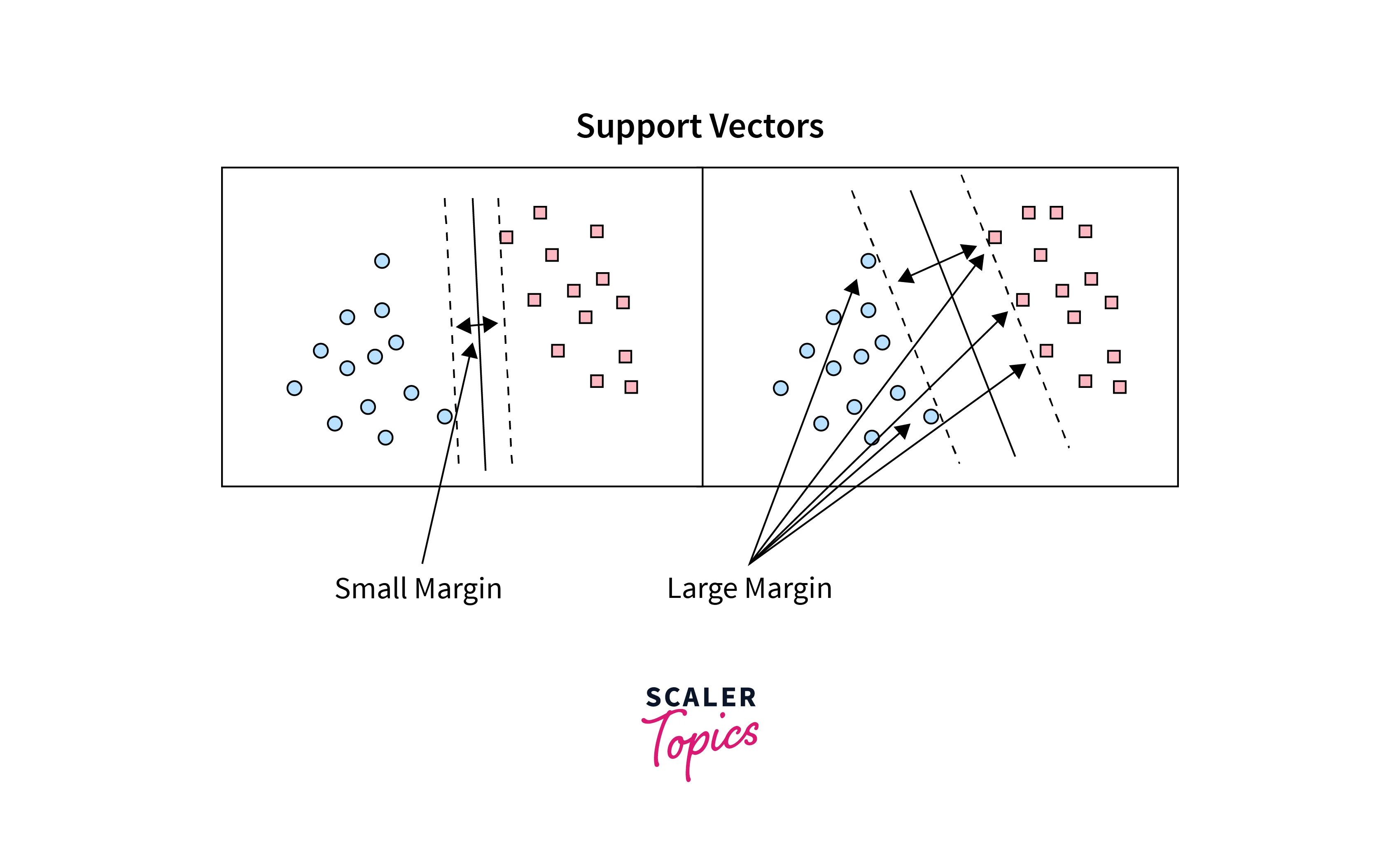
For an n-dimensional plane, a hyperplane is an (n-1) dimensional plane that divides it into two parts. For 1D, it is a point. For a 2D scenario, a hyperplane is a line. For 3D, it's a plane. Beyond 3D, the representation of a hyperplane is not possible. Hyperplane and Support Vectors in SVM

Support Vectors

Support vectors are samples closer to the hyperplane. It decides the location and orientation of the hyperplane. Using these support vectors, SVM maximizes the margin of the classifier. The addition or Deletion of the support vectors will change the position of the hyperplane.

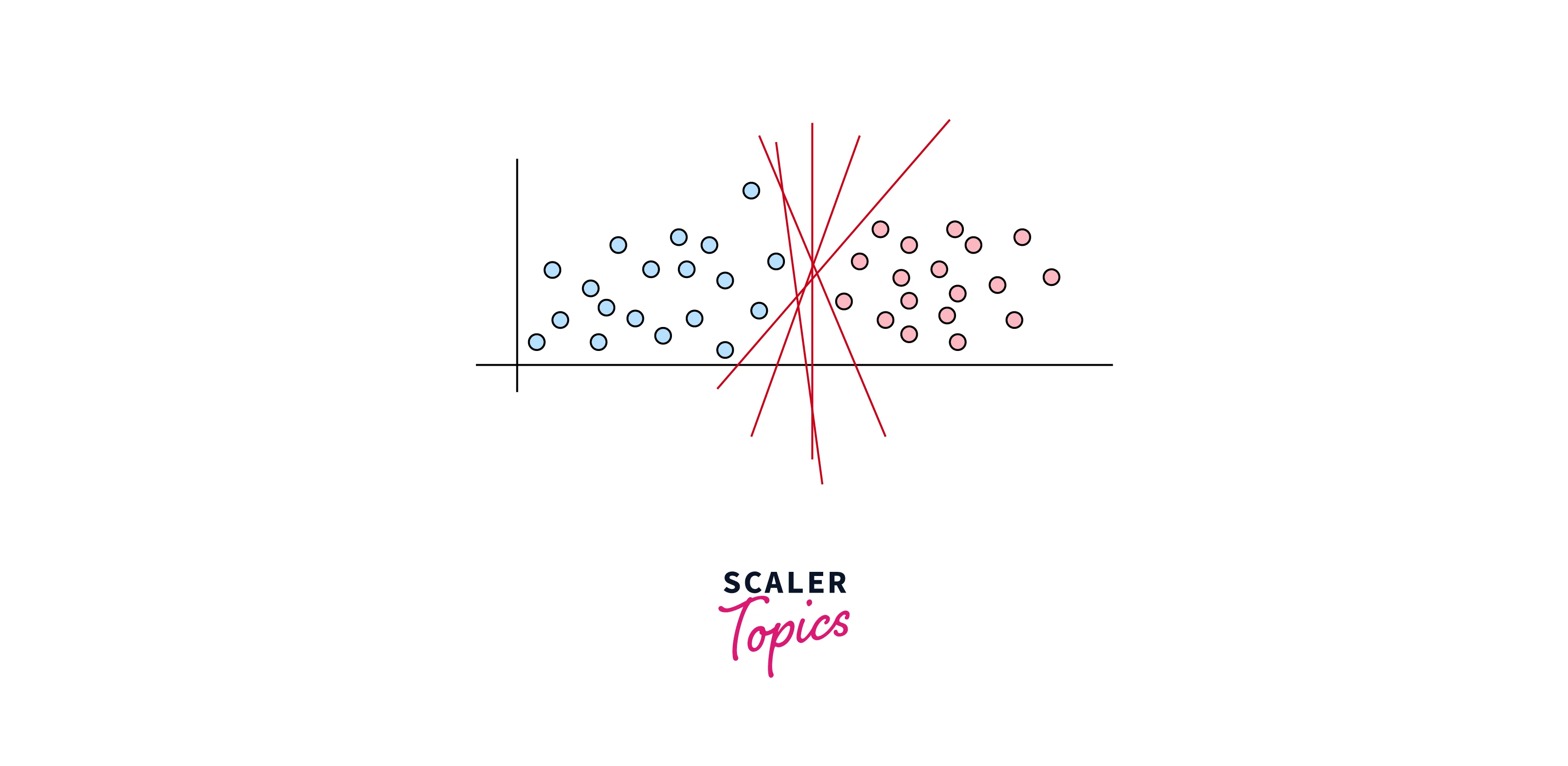
Selecting the Best hyperplane

Let us try to understand this with an example first. Given data from two linearly separable classes, one can draw many hyperplanes that correctly identify all samples. The SVM algorithm chooses the one from many possible hyperplanes, which maximizes the distance from all the classes' nearest data points. Selecting the Best hyperplane

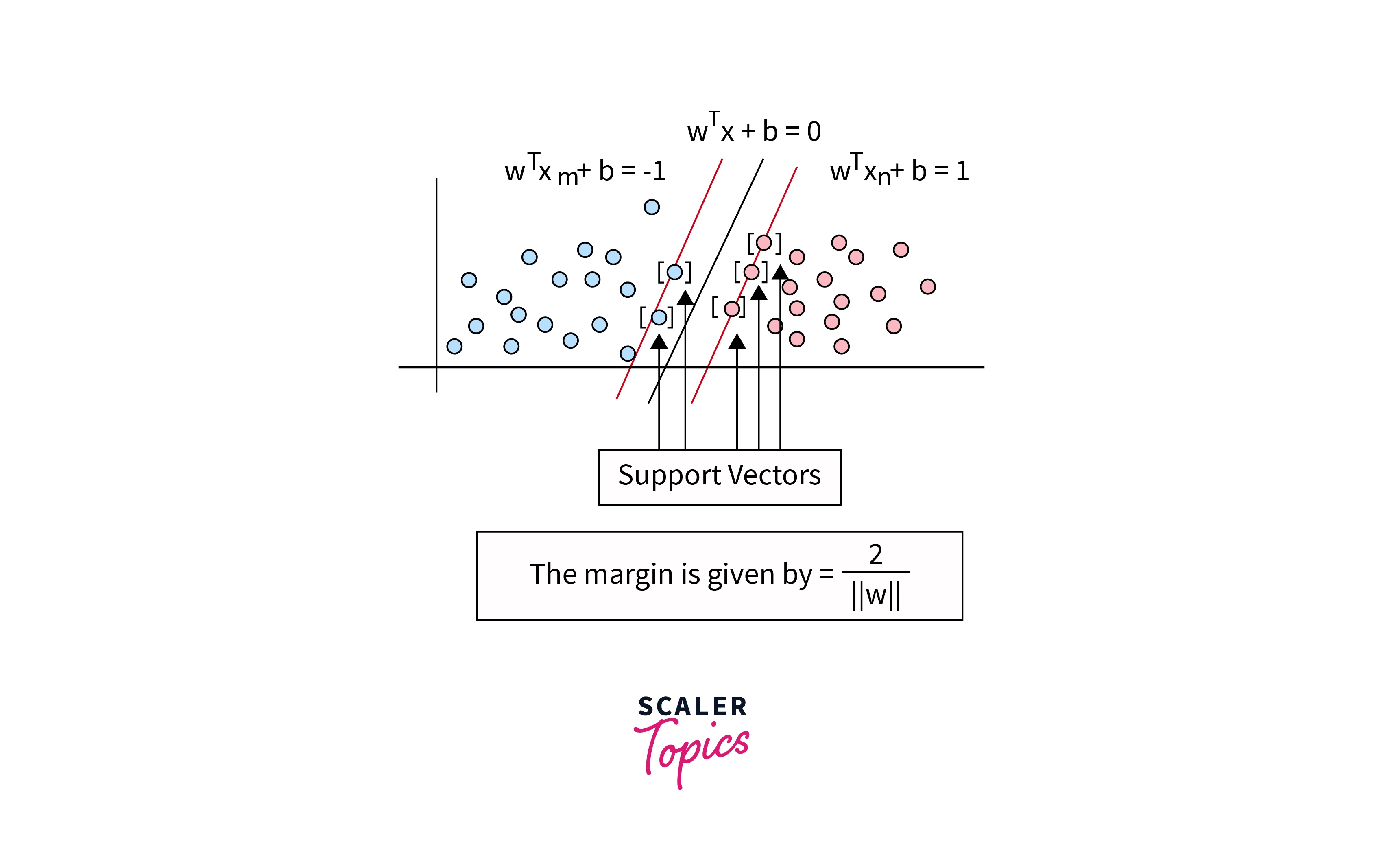
Mathematical Equation

Here, the equation for left-hand side (class label $y^i=-1$ ) support vector can be written as $w^Tx_m + b =-1$ ....(1), and for right hand side (class label $y^i=+1$ ) it is $w^Tx_n + b =1$ ....(2). Hence, The margin $(x_n-x_m)=2/||w||$ . We are interested in finding values for w and b that maximize the margin. Note that, equations 1 and 2 can be combined and extended for all sample $x_i$ as $y^i(w^tx_i+b) \ge 1$ .... (3) Maximizing the margin means minimizing $w^Tw/2$ such that the constraint in equation 3 is satisfied. Selecting the Best hyperplane mathematical equation Hence our objective function becomes minimise $w^Tw/2$ such that, $y^i(w^tx_i+b) \ge 1$ for all $x_i$ . Using the Lagrangian Multiplier and KKT Condition, we can solve the equation to identify the best hyperplane.

SVM Implementation in Python

Let us first import the necessary library.

Next, we will generate a toy data sample for our classification purpose.

Let's visualize how the data looks.

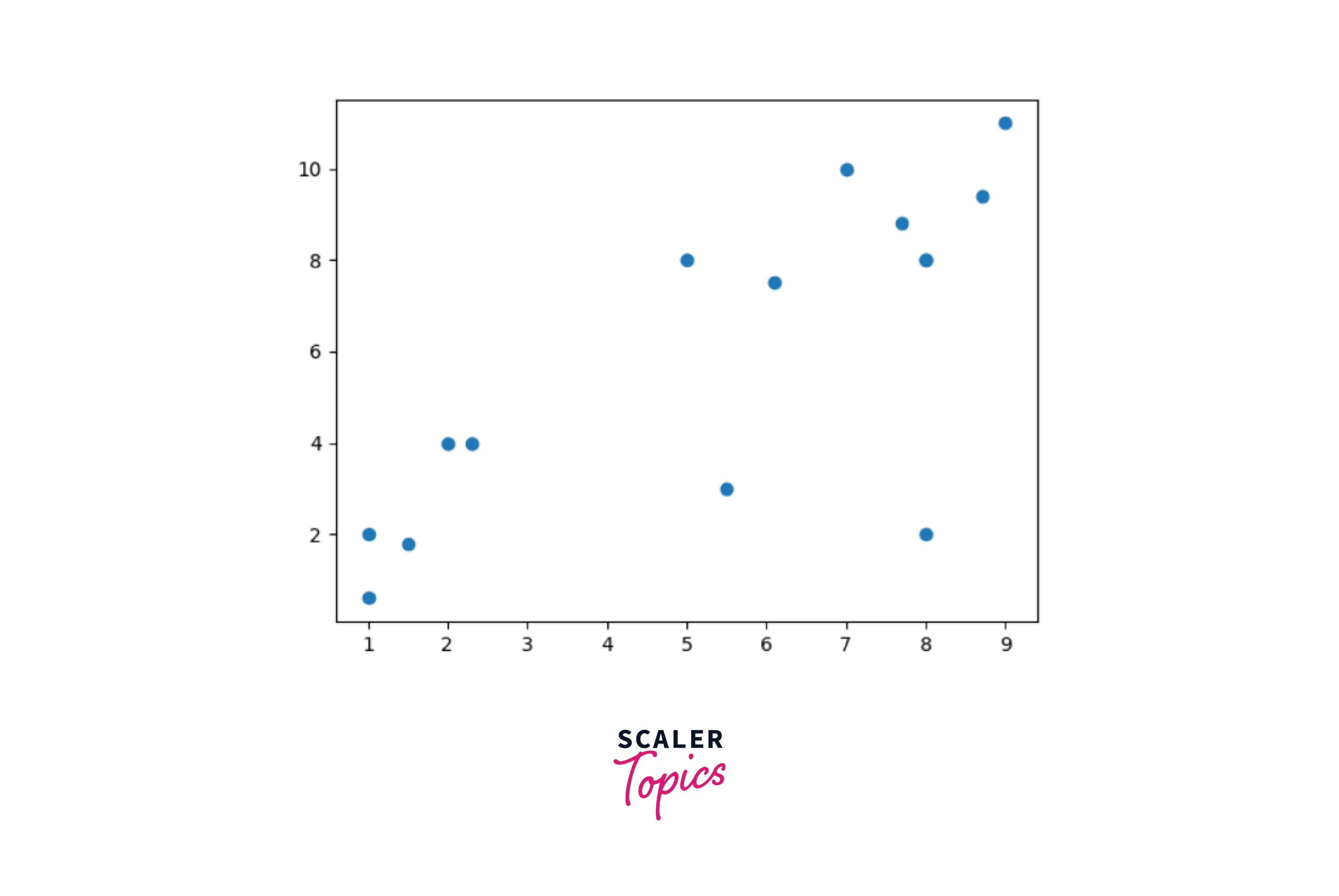
SVM implementation in python

Class labels are added to each sample so that it remains linearly separable.

Next, let's create the classification model and feed the training data into the model.

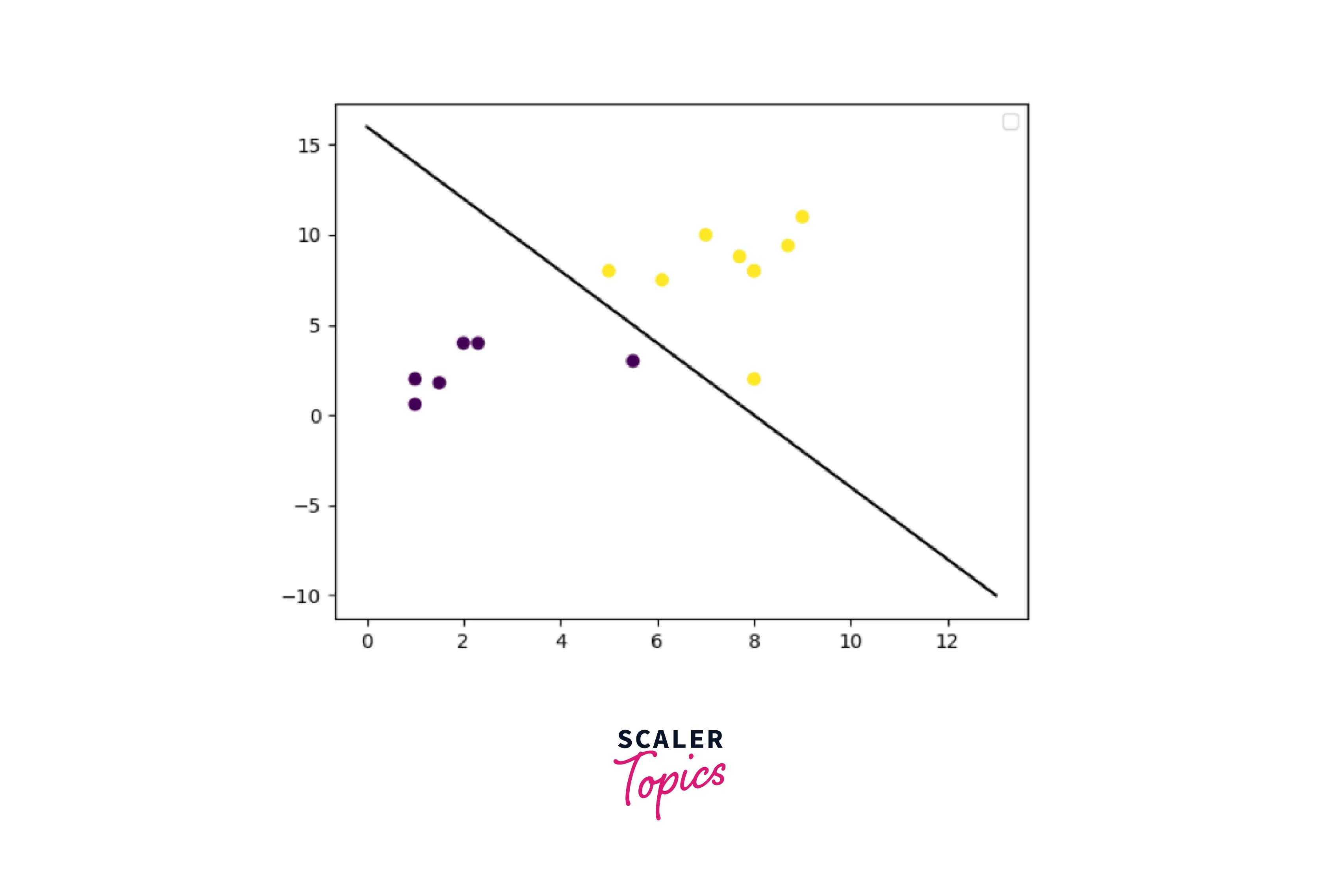
Next, the trained model predicts the class and draws the decision boundary.

The output of the above snippet is shown below. SVM implementation in python 2

Conclusion

You have learned about linear support vector machine here, a popular and crucial supervised machine learning algorithm.
For ease of understanding, we have presented a python implementation of a linear support vector machine.
Nonlinear support vector machine will be covered in a subsequent lecture.