Mathematical Operations on Images in Computer Vision

Introduction

Fundamental operations used in computer vision to analyze and evaluate images are mathematical operations on images in computer vision. Mathematical processes like addition, subtraction, multiplication, division, and matrix operations are frequently utilized in computer vision. Operations, including image enhancement, segmentation, feature extraction, and object recognition, can be accomplished using these methods.

Image Representation

An image comprises a rectangular array of dots known as pixels and is also defined as a two-dimensional function. To represent digital images, we mostly use two methods. Suppose a digital image with M rows and N columns is created by sampling the image f(x, y). The values of the coordinates (x, y) are now discrete quantities. We will utilize integer values for these discrete coordinates to simplify the notation and make things easier. As a result, the coordinates at the origin have the values (x, y) = (0, 0). The following coordinate values along the image’s first row are shown as (x, y) = (0, 1). It’s crucial to remember that the second sample along the first row is denoted by the notation (0, 1). It doesn’t necessarily imply that these were the physical coordinate values when the image was captured.

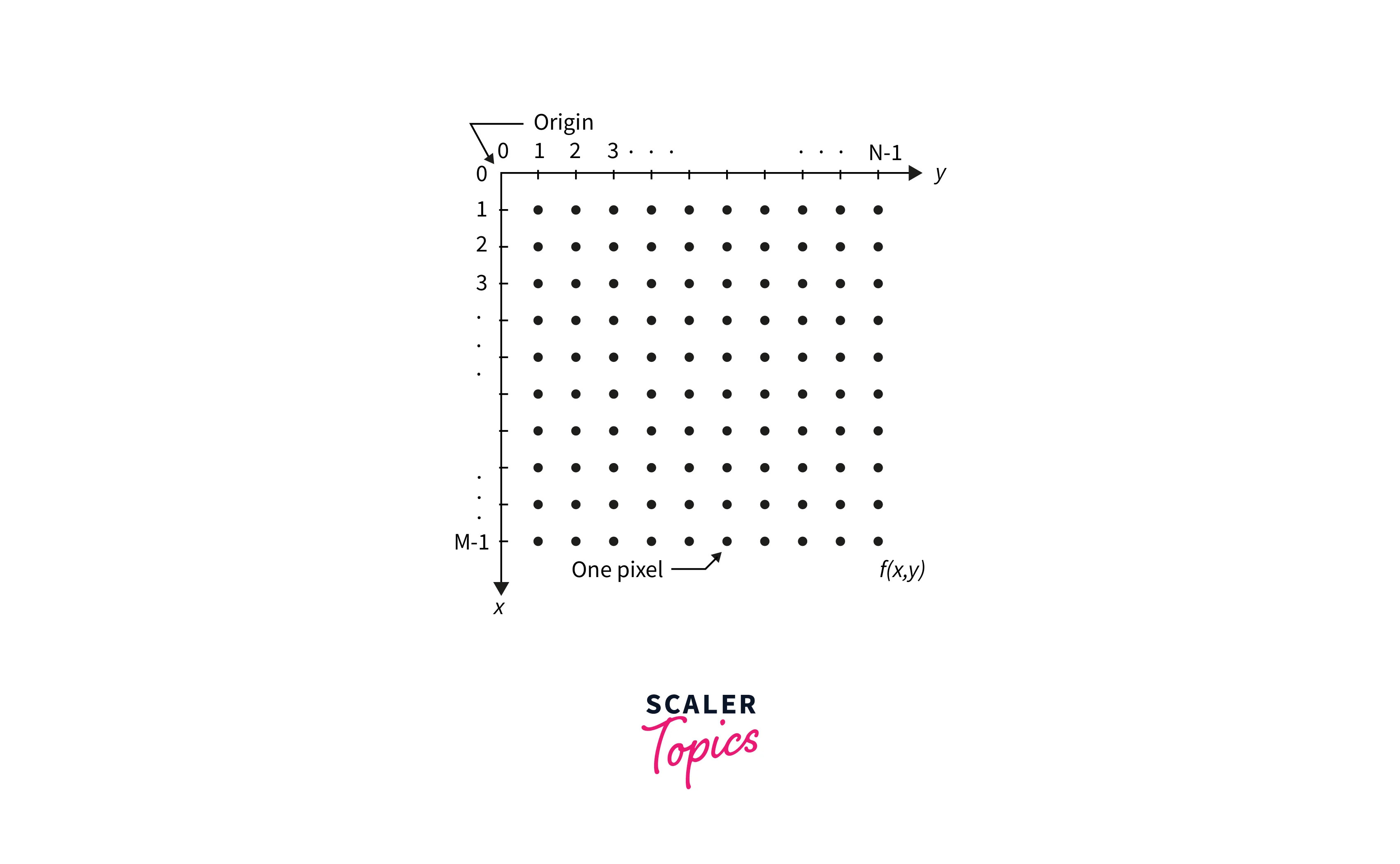
Types of Image Representation

Image As a Matrix:

Going on to how an image is represented, the most basic method you may have already considered is to express an image as a matrix. An image is a set of square pixels (picture elements) arranged in columns and rows in an array or matrix. The elements in these arrays or matrices also represent the pixels or intensity values of the image.

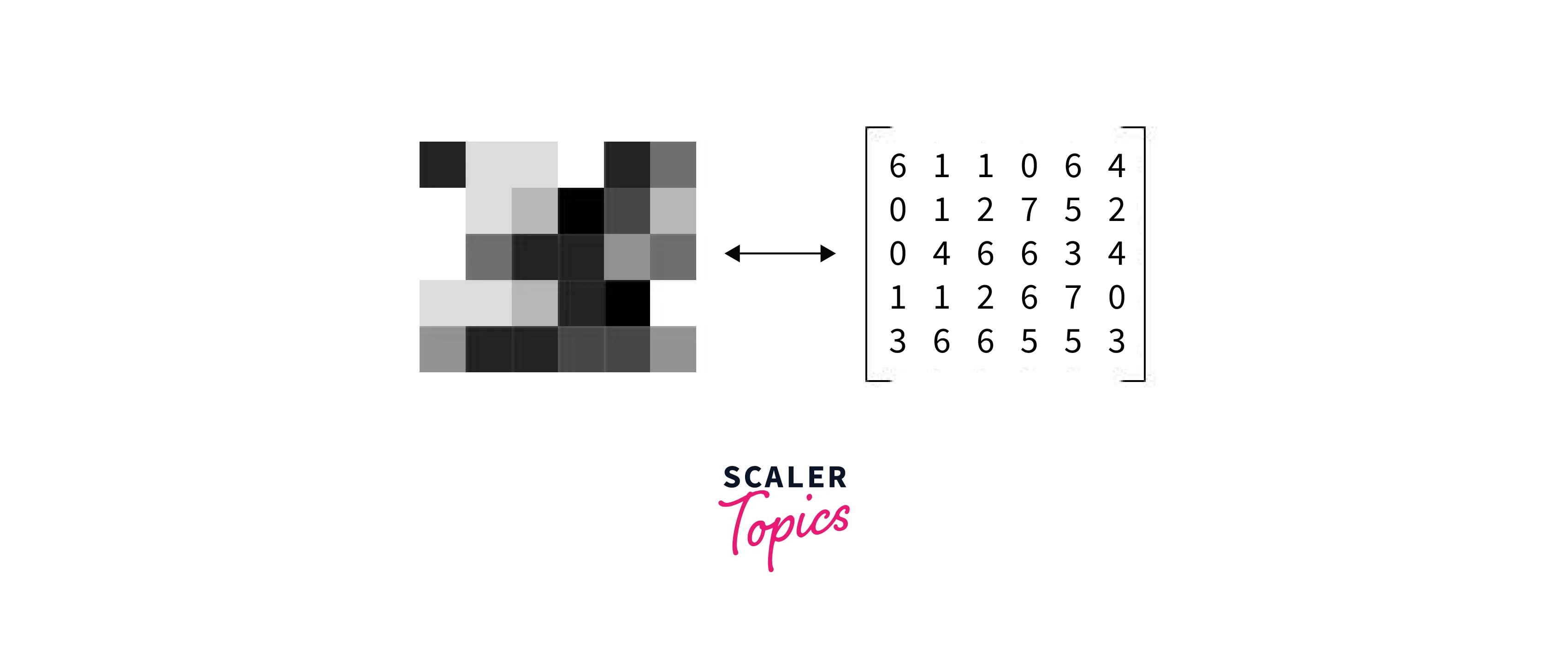
People frequently used up to a byte to represent each pixel in an image. This means that 0 is black and 255 is white, and values between 0 and 255 reflect the intensity for each pixel in the image. A matrix of this kind is constructed for each color channel in the image. Normalizing numbers between 0 and 1 is also typical.

Image as a Function:

In its most general form, an image is a function f from R2 to R (f: ℝ² → ℝ).It just helps us have operations on images more effectively if we represent it also as a function. A function(f) being going fromR 2 to R, which simply corresponds to one particular coordinate location on the image, say (i, j) and that is what we mean by R2 – f( x, y ) gives the intensity of a channel at position (x, y) , that is If values are normalized, the intensity value can range from 0 to 1 or from 0 to 255. – defined over a rectangle, with a finite range: f: [a,b]x[c,d] → [0,1] – A color image is just three functions pasted together:

• f( x, y ) = (fr( x, y ), fg( x, y ), fb( x, y ))

Advantages and Disadvantages of Image Representations

• It relates to how the transmitted information, such as color, is digitally coded and how the image is saved, i.e., how an image file is structured.
• For the successful identification and recognition of items in a scene, image representation and description are essential.
• Digital images can be modified using matrices since they are matrices when broken down into the finest bits of information (pixels).
• The matrix format of an image also enables operations like brightness addition and rotation.
• Also, because the color value information is readily available and well-organized, filters that can alter an image's coloring are simple to apply.
• Image processing has benefited tremendously from matrix manipulation.
• Matrix only accepts photos in.jpg or.jpeg format. The system won't accept other file types, including those that are based on the.jpg standard, like.png.
• Every image that is processed by Matrix uses the sRGB color profile. Nevertheless, photographs with an "Uncalibrated" Color Representation or any other mentioned standard may be "color shifted" or lose quality during upload. Images with no Color Representation defined may be used.
• This is the suggested minimum size because Matrix saves all listing photos at 2048 pixels wide by 1536 pixels tall. 3000 by 3000 pixels is the largest size that Matrix will accept. Pictures that are larger than 3000 pixels in either direction may not upload.
• Image Transformation is possible when an image is represented as a function.

Basic Mathematical Operations

Image arithmetic or mathematical operation on images is a method of manipulating images by applying ordinary arithmetic or logical operators. Each pixel's value in the output image is solely determined by its matching pixel in the input images since these processes are carried out pixel-by-pixel. The input images must normally be the same size as a result. When adding an offset to an image, for example, one input image could be a constant value.

Despite being a straightforward method of image processing, image arithmetic has many uses. Due to its simplicity, one of its key benefits is speed. For example, when reducing random noise by adding successive images or detecting motion by subtracting two successive images, the images being processed are often snapshots of the same scene recorded at various times.

In image arithmetic, logical operators are frequently employed to join binary images. Logical operators are often applied bitwise when working with integer pictures. This enables the use of a binary mask to choose particular areas inside an image.

Addition and Subtraction of Images

The OpenCV function cv2.add() or the straightforward numpy operation addition = image1 + image2 can be used to combine two images. Both images should be of the same depth and type, otherwise, the second image can simply be a scalar number. But, adding the pixels is not optimal. As a result, we employ the cv2.addweighted() function.

Output

subtraction of images With cv2.subtract, we may subtract the pixel values from two images and merge them . The images must be the same size and depth. It is customary to use a single image as input and to subtract a constant value from all of the pixels.

Output

Multiplication and Division of Images

Multiplication Multiplication is used in computer vision to scale images and perform transformations such as rotation and scaling. It's also utilized in image processing processes like convolution and correlation. Multiplication is a computationally efficient operation, particularly when performed with SIMD (Single Instruction Multiple Data) instructions.

Using the cv2.multiply() function, we achieve picture scaling by multiplying the first image by 0.5. The cv2.multiply() function performs element-wise multiplication of the image's pixel values.

Scaling images using multiplication operation

Output

Division In computer vision, the division is used for image normalization and contrast adjustment. It is also employed in several feature extraction methods. When working with huge images, the division might be computationally expensive.

Below is an example of implementing the division of images for normalization

Output

Blending of Images

This is likewise image addition, but the images are given varied weights to create the illusion of blending or transparency. The first image weights 0.7, whereas the second image has a weight of 0.3.

Output BLENDED IMAGE

Comparison of Basic Mathematical Operations

• Image processing operations such as blending and background subtraction make use of addition and subtraction.
• Scaling, blending, filtering, and feature extraction all rely on multiplication.
• Normalization, contrast adjustment, and colour balance are all accomplished by division.
• Subtraction and division are not commutative, but addition and multiplication are.
• Subtraction and division are not associative, although addition and multiplication are.
• Subtraction and division are distributive over each other, but addition and multiplication are not.
• Each operation has distinct properties and applications, and a combination of these operations is frequently utilised to do more complicated computer vision tasks.

Advanced Mathematical Operations

Advanced mathematical operations are an essential part of computer vision and image processing. They allow us to extract useful information from images, detect patterns, and perform complex tasks like object recognition and tracking. These operations can be used to perform tasks like image filtering, segmentation, feature extraction, and classification.

Image Filtering

• The process of enhancing, blurring, or sharpening images.
• Involves a kernel or filter mask convolving an image.
• The Gaussian, Sobel, and Laplacian filters are typical filters.
• Moreover, non-linear filters like median and bilateral filters are frequently employed.

Convolutional Operations

• A mathematical operation used to extract features from an image.
• involves applying a number of learnable  filters to a given image.
• Semantic segmentation, object detection, and image classification are typical uses.
• A few well-known convolutional neural networks are MobileNet, ResNet, VGG, and AlexNet.

Fourier Transform

• The technique for converting images from the spatial to the frequency domain.
• Involves breaking down an image into its individual frequency components.
• Edge detection, noise reduction, and image compression are typical uses.
• In image processing, the discrete Fourier transform (DFT) and fast fourier transform (FFT) are frequently utilized.

Wavelet Transform

• The technique for converting images from the spatial to the frequency domain.
• Involves breaking an image down into many wavelets with various sizes and orientations.
• Image compression, feature extraction, and denoising are frequent uses.
• There are several wavelet families that are often utilised, including Haar, Daubechies, and Coiflets.

Comparison of Advanced Mathematical Operations

• It is essential to keep in mind that each of these sophisticated mathematical operations has distinct properties and applications while comparing them.
• Convolutional operations are utilised for feature extraction in many image processing tasks, whereas image filtering is effective for enhancing, blurring, or sharpening images.
• Wavelet transformations are better suited for images with localized features than Fourier transforms, which are utilised for frequency analysis and image compression.
• The particular challenge and the characteristics of the input image will influence the approach selection.

Applications of Mathematical Operations

Mathematical operations are used extensively in computer vision to extract meaningful information from images. These operations can be used to filter noise, enhance image quality, and segment objects from backgrounds.

Image Enhancement

Image enhancement is the process of raising an image's quality and aesthetic appeal. By modifying contrast, brightness, and sharpness, and reducing noise, mathematical operations contribute significantly to image enhancement. The following are some instances of mathematical processes applied to improve images.

1. Contrast stretching
2. Histogram Equalization

Image Restoration

The process of eliminating noise or artifacts from an image to restore its original quality is known as image restoration. For image restoration, mathematical processes like deconvolution and filtering are frequently utilised. The following are a few instances of mathematical processes used for image restoration:

1. Median Filtering
2. Wiener Deconvolution

Image Segmentation

The technique of splitting an image into many segments or regions based on similar qualities such as color, texture, and form is known as image segmentation. Image segmentation frequently makes use of mathematical procedures including thresholding, edge detection, and morphological processes. Here are the instances of mathematical processes that are applied to image segmentation:

1. Thresholding
2. Edge Detection

Object Recognition and Detection

The methods of locating and detecting things in an image are known as object recognition and detection. For object recognition and detection, mathematical processes including feature extraction, template matching, and convolutional neural networks are frequently utilised. The following are the instances of mathematical operations used for item identification and detection:

1. Feature Extraction
2. Convolutional Neural Networks

Challenges and Future Scope

• The requirement to manage vast volumes of data can be computationally taxing and demands specialized hardware and software, which is one of the main issues in the subject of mathematical operations in computer vision.
• The requirement to manage vast volumes of data can be computationally taxing and demands specialized hardware and software, which is one of the main issues in the subject of mathematical operations in computer vision.
• Creating algorithms that can efficiently process and evevaluateeterogeneous image data, including images from multiple sensors and modalities, including infrared and medical imaging, is another difficulty.
• The development of effective and scalable algorithms that are capable of handling data sets that are more complicated and different will determine the future application of mathematical operations in computer vision.
• The combination of mathematical processes with other technologies, such machine learning and artificial intelligence, to produce more intelligent and adaptive computer vision systems, is another area of future growth.