How to Plot Polar Axes in Matplotlib?

Introduction

The polar coordinate system plots angular data on the graph, i.e., periodic functions. A point in the polar coordinate system is represented as ($r,\theta$), where r is the distance from the origin and theta is the angle from the axis. matplotlib.pyplot.polar() is used to plotting curve on polar axes.

When to use Polar Coordinates

The two most popular methods for plotting the points on a graph are the rectangular and polar coordinate systems. Polar coordinates are best used when periodic functions are considered. The polar coordinates of points describe their position in terms of distance from the origin and a fixed direction (angle).

Using a rectangular coordinate system when dealing with latitude and longitude would be impractical. Suppose we point out the location of a spherical object. In that case, we use polar coordinates because it will pinpoint the location with more accuracy, distance from the center of the spherical object, and angle from the axes.

Similarly, in a GPS, the concept of polar coordinates is used to find the real-time location of a person. Moreover, many physical systems—such as those concerned with bodies moving around a central point or phenomena originating from a central point—are simpler and more intuitive to model using polar coordinates.

Angular Data

For plotting the polar coordinates on the polar coordinate system, we need two things, $r$ and $\theta$, where $r$ is the distance from the origin to the point, and the $\theta$ is the angle of projection of the point to the x-axis.

Example: Plotting angular data on the polar coordinate system

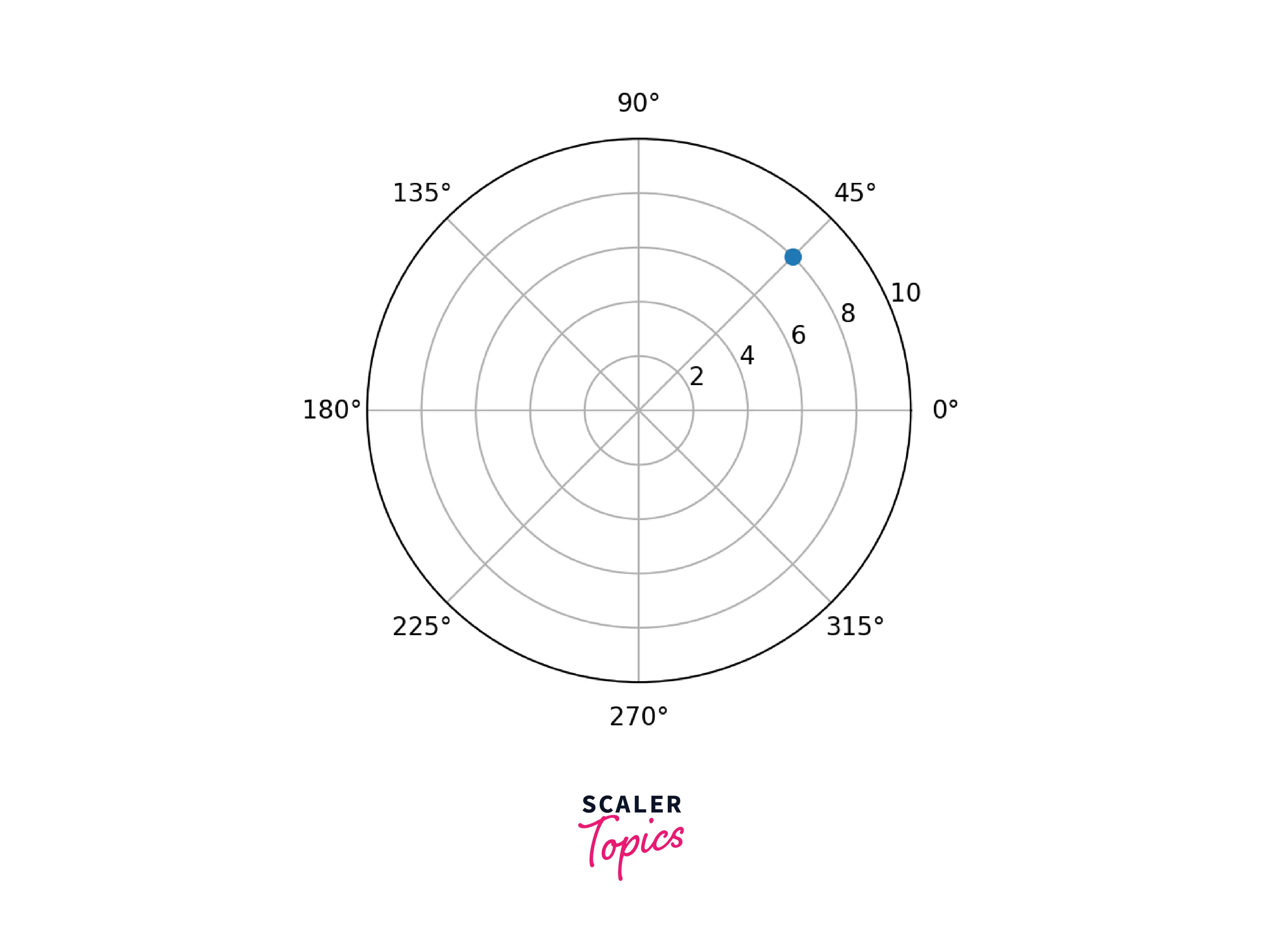
In the above plot, this is how a polar coordinate system looks: angles are the x-axis and the distance from the origin to the circle's circumference is the y-axis. As we can see, there is a marker on the coordinate system. It is a polar coordinate where r=8 and theta=45°.

How to Plot Polar Axes in Matplotlib

How does it Work?

Before plotting polar coordinates on the graph, we have to change the coordinate system from rectangular to polar, which can be done by using the function matplotlib.pyplot.axes(projection =) where we must pass the value 'polar' in the parameter projection. The matplotlib.pyplot.polar() function pyplot modules are used to plot polar coordinates. This function plots various figures like circles, ellipses, cardioid, and the archimedean spiral. It takes at least two parameters to plot the polar coordinates on the graph, i.e., r and theta.

Syntax and Parameters

Syntax of the function to plot polar coordinates is

Parameters of the function,

• theta: Angle by which we plot the point.
• r: Distance between the origin and point.
• kwargs: Keyword argument to change the visual properties of the points like a marker, color, size, width, etc.

How to Plot Data on a Polar Coordinate System

Below is the implementation of plotting points on polar axes in matplotlib.

Output:

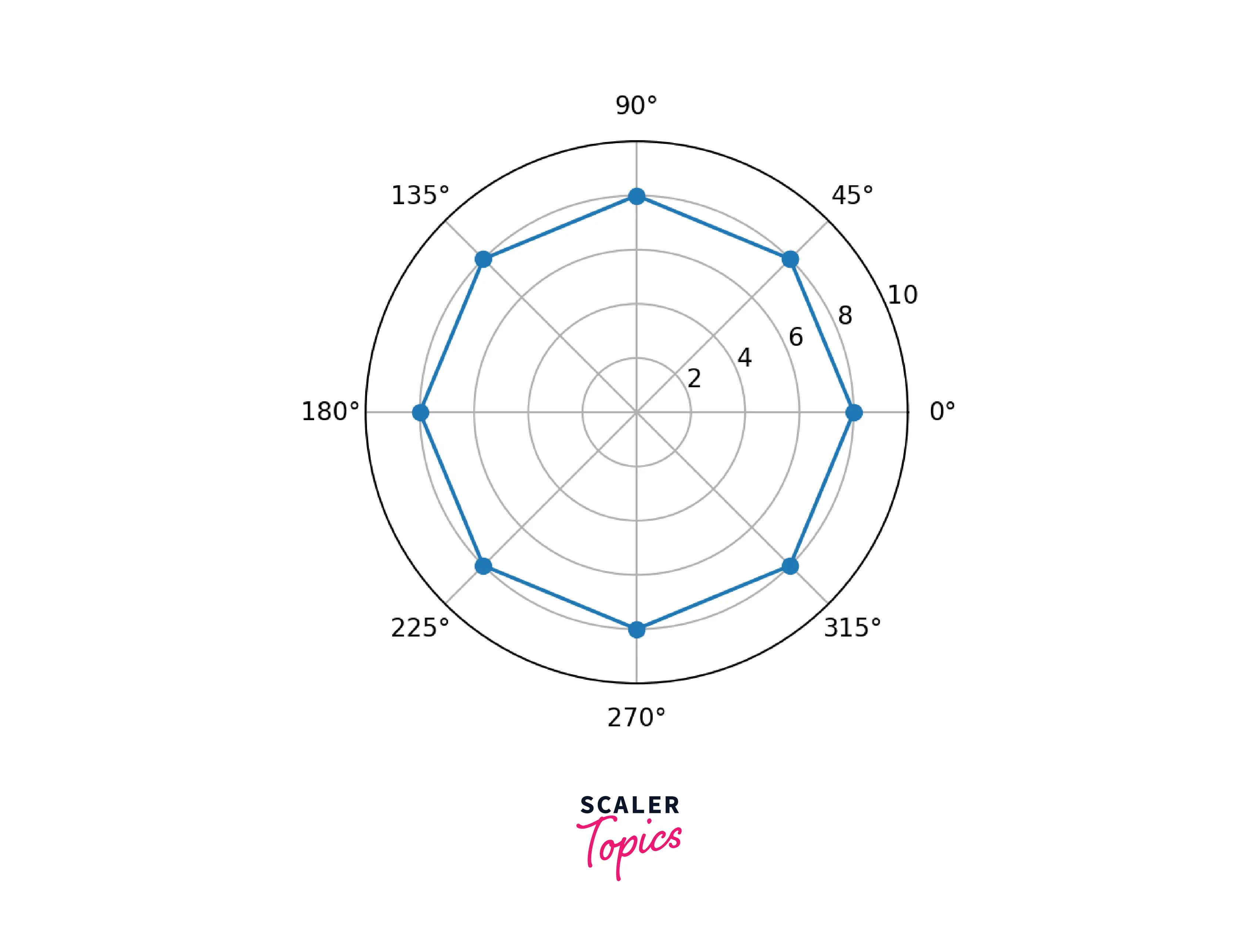
Code explanation:

• Importing the required modules.
• Creating the new figure and setting up the resolution using the function matplotlib.pyplot.figure(dpi=).
• Adding the subplots to the created figure and set the coordinate system to polar by setting the value of the parameter projection to 'polar'.
• Then, generate the r and theta and store them in the list.
• Plot the point on the polar coordinate system using the function matplotlib.pyplot.polar().
• Then, set the y-axis tick range using the .add_subplot().set_ylim function.
• Displaying the plot using the matplotlib.pyplot.show() function.

Common Examples

Polar Projections

Polar projections are some plots that can be plotted on a polar coordinate system example, a circle, an ellipse, or an archimedean spiral.

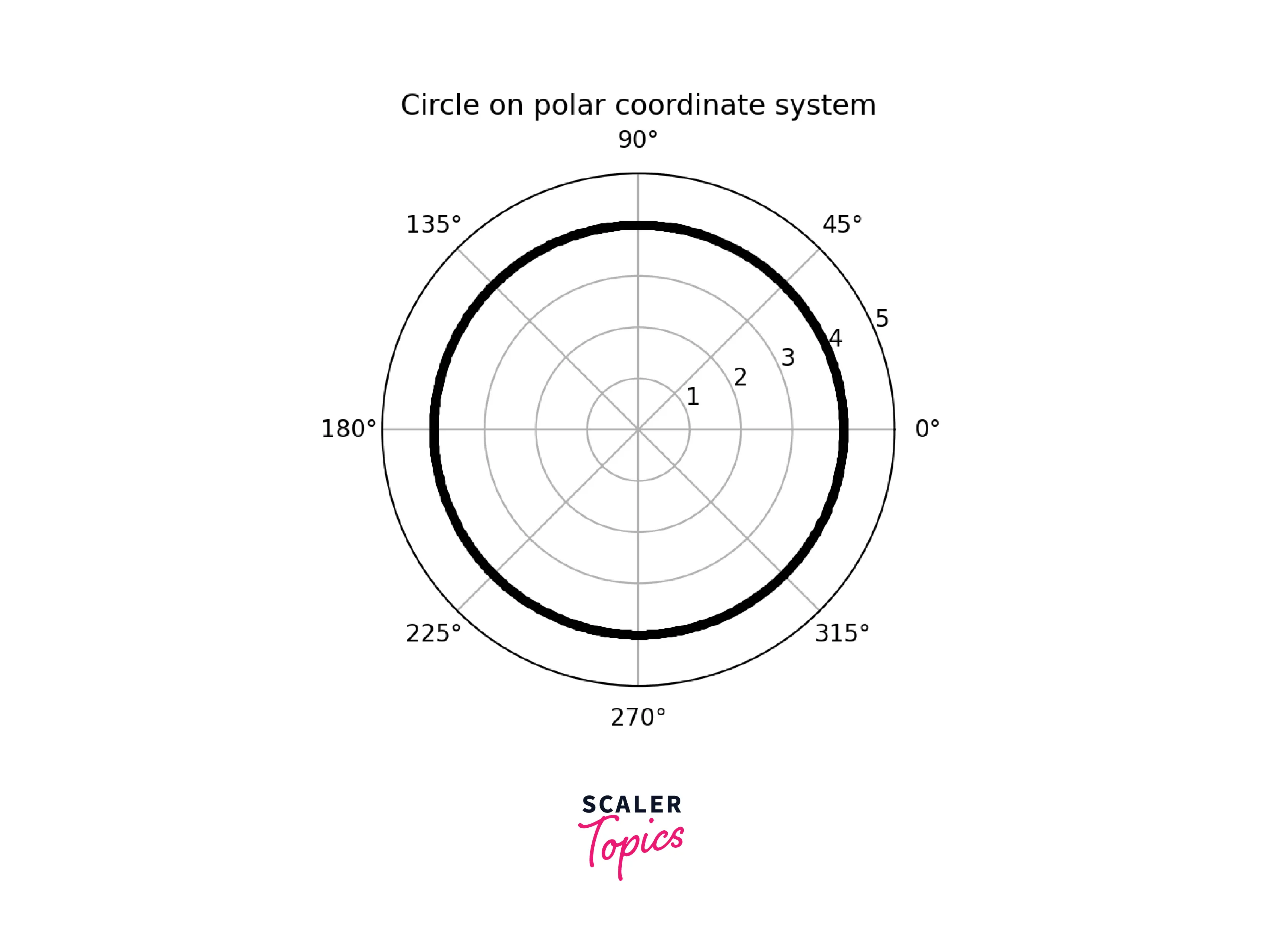
Example 1: Drawing a circle on a polar coordinate system

For Drawing a circle on the polar coordinate system, we need a radius and a list of angles from 0 to 2π in a very short interval.

Output:

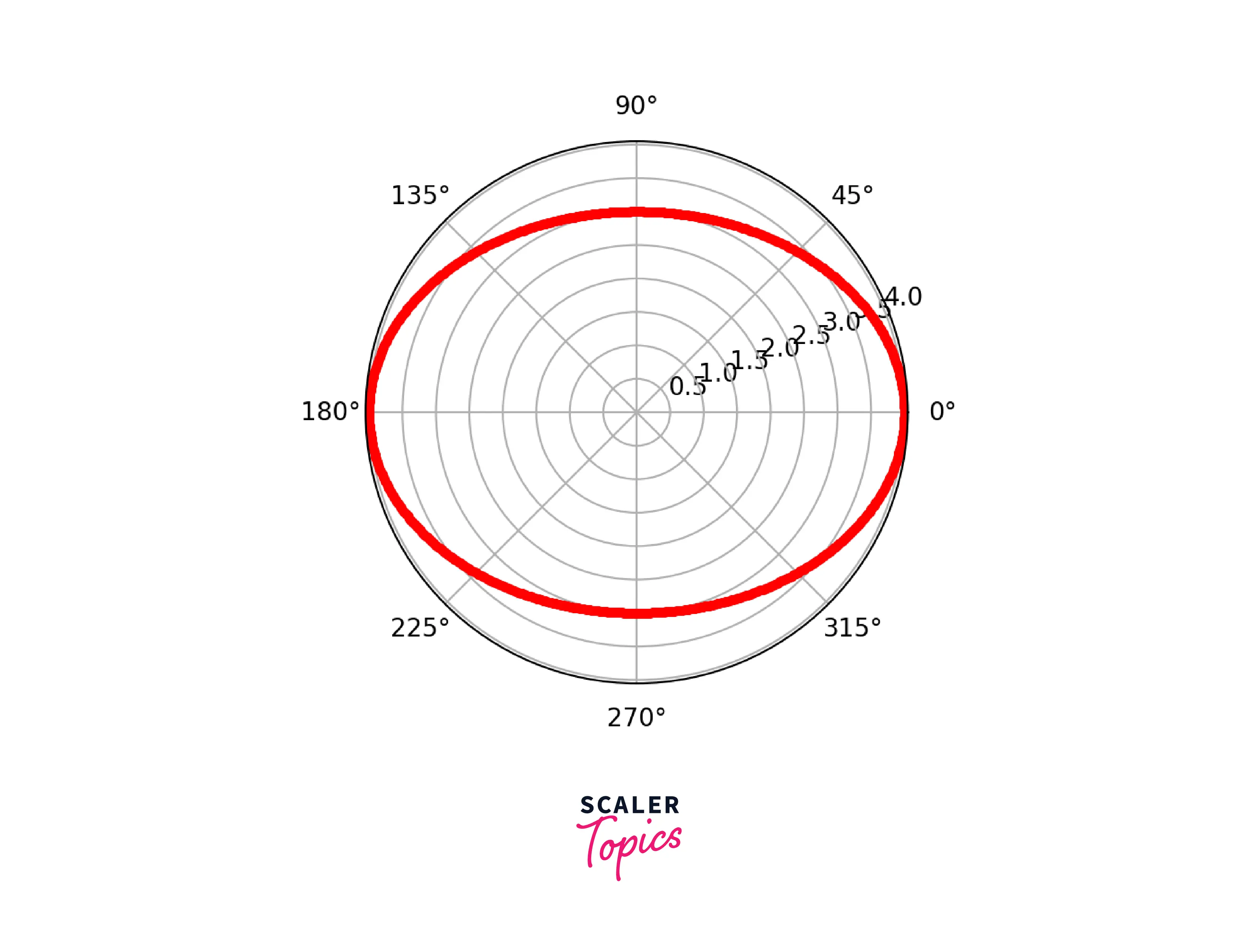
Example 2: Drawing an ellipse on polar coordinates

An ellipse is a locus of a point moving in a plane such that the sum of its distances from two other points (the foci) is constant. Here, r is defined as:

$r= \frac {a*b}{\sqrt{(asin\theta)^2 + (bcos\theta)^2)}}$

Where,

a = length of the semi-major axis b = length of the semi-minor axis

Output:

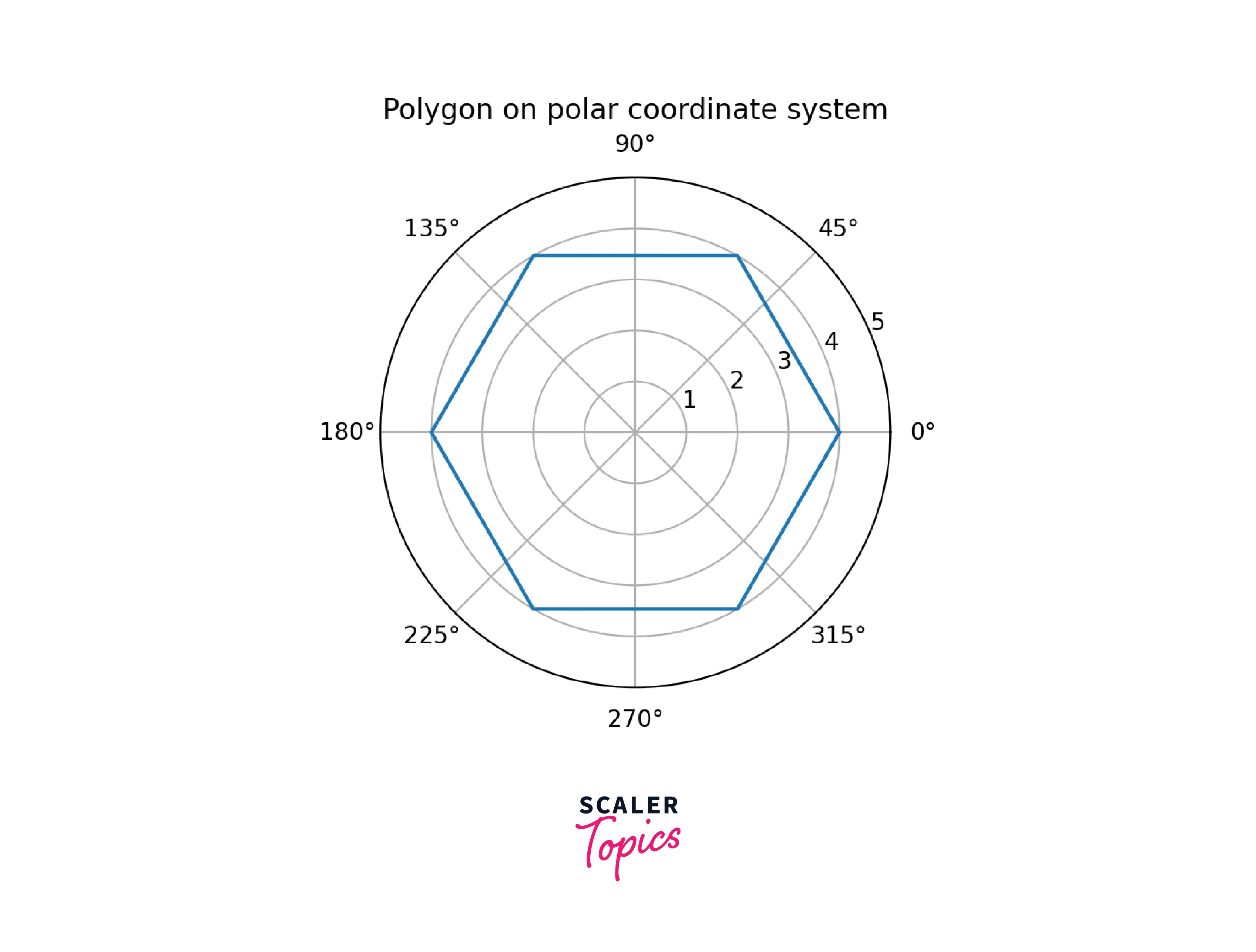
Polygons

Example: Implementation of the polygon in matplotlib

Output: