Matrix Chain Multiplication

The number of multiplication steps required to multiply a chain of matrices of any arbitrary length $n$ highly depends on the order in which they get multiplied.

As multiplication of two numbers/integers is a costly operation, it is very much needed to find the optimal order of multiplying a chain of matrices to minimize the multiplication steps, which ultimately optimizes the time and resources required for the task.

Introduction to Matrix Chain Multiplication

In linear algebra, matrix chain multiplication is an operation that produces a matrix from two matrices. But, multiplying two matrices is not as simple as multiplying two integers, certain rules need to be followed during multiplying two matrices.

Let’s say we have two matrices, $X$ of dimensions $x_1\times x_2$ and $Y$ of dimensions $y_1\times y_2$. $X$ and $Y$ can be multiplied if and only if $x_2=y_1$. And if the condition satisfies the resultant matrix (say $P$) will be of dimension $x_1\times y_2$ and it requires $x_1\times x_2\times y_2$ multiplication steps to compute $P$.

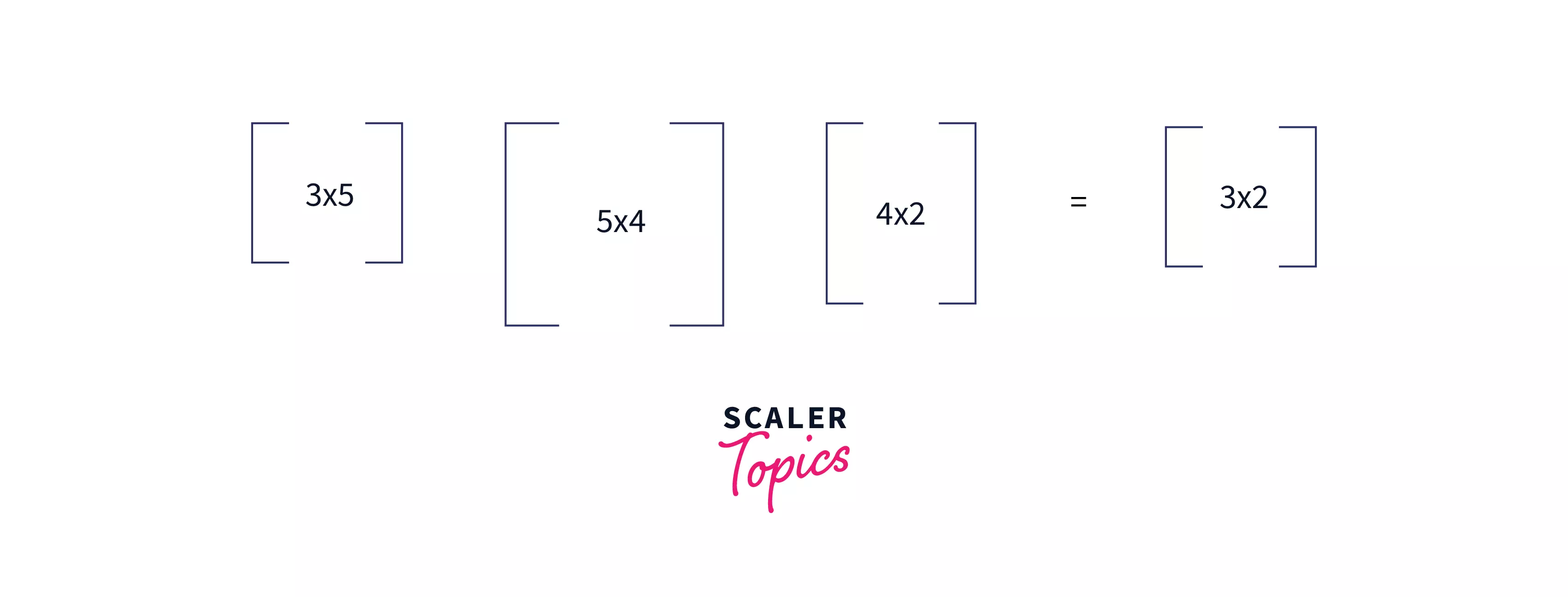
If we have been given a chain of matrices of some arbitrary length ‘$n$’, the number of multiplication steps required to multiply all the matrices highly depends on the order in which we multiply them.

So, in the matrix chain multiplication problem, we have been given an array representing the dimension of matrices $[M_1,M_2,\dots ,M_n]$ and we are interested to deduce the minimum number of multiplication steps required to multiply them.

Example of Matrix Chain Multiplication

We have studied in our school days that matrix chain multiplication follow associative rule $i.e.$ $(M_1\times M_2)\times M_3$$=$$M_1\times (M_2\times M_3)$ and the number of steps required in multiplying matrix $M_1$ of dimension $x\times y$ and $M_2$ of dimension $y\times z$ are $x\times y\times z$, and the resultant matrix $M_{12}$ is of dimension $x\times z$

Let’s assume we have three matrices $M_1,M_2,M_3$ of dimensions $5\times 10$, $10\times 8$, and $8\times 5$ respectively and for some reason we are interested in multiplying all of them.
There are two possible orders of multiplication –

• $M_1\times (M_2\times M_3)$
  • Steps required in $M_2\times M_3$ will be $10\times 8\times 5$ $=$ $400$.
  • Dimensions of $M_{23}$ will be $10\times 5$.
  • Steps required in $M_1\times M_{23}$ will be $5\times 10\times 5$ $=$ $250$.
  • Total Steps $=$ $400+250$ $=$ $650$
• $(M_1\times M_2)\times M_3$
  • Steps required in $M_1\times M_2$ will be $5\times 10\times 8$ $=$ $400$.
  • Dimensions of $M_{12}$ will be $5\times 8$.
  • Steps required in $M_{12}\times M_3$ will be $5\times 8\times 5$ $=$ $200$.
  • Total Steps $=$ $400+200$ $=$ $600$

Here, if we follow the second way, we would require $50$ fewer operations to obtain the same result.

Hence, it is necessary to know the optimal way in order to speed up the multiplication process by placing the brackets at every possible place and then checking which positioning minimizes the effort.

Naive Recursive Approach

The idea is very simple, placing parentheses at every possible place. For example, for a matrix chain $M_1{M}_2{M}_3{M}_4$ we can have place parentheses like –

• $(M_1)(M_2{M}_3{M}_4)$
• $(M_1{M}_2)(M_3{M}_4)$
• $(M_1{M}_2{M}_3)(M_4)$

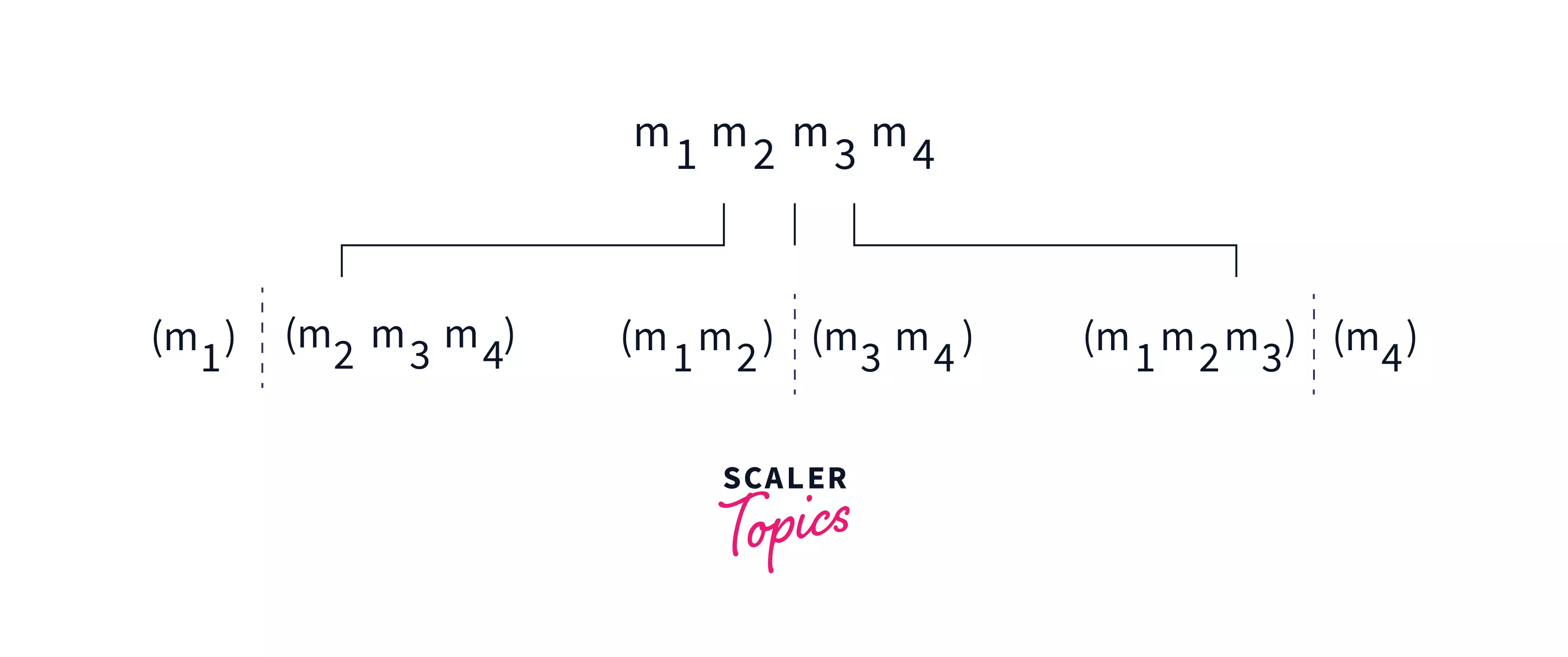
So for a matrix chain multiplication of length $n$, $M_1{M}_2\dots M_n$ we can place parentheses in $n-1$ ways, notice that placing parentheses will not solve the problem rather it will split the problem into smaller sub-problems which are later used to find the answer for the main problem.

Like in $(M_1)(M_2{M}_3{M}_4)$ the problem is divided into $M_1$ and $(M_2{M}_3{M}_4)$ which can be solved again by placing parentheses and splitting the problem into smaller sub-problems until size becomes less than or equal to 2.

So we can deduce the minimum number of steps required to multiply a matrix chain of length $n$ $=$ minimum number of all $n-1$ sub-problems.

To implement it we can use a recursive function in which we will place parentheses at every possible place, then in each step divide the main problem into two sub-problems $i.e.$ left part and right part.

Later, the result obtained from the left and right parts can be used to find the answer of the main problem.
Let’s have a look at Pseudocode for better understanding.

Pseudocode of Recursive Approach

// mat = Matrix chain of length n
// low = 1, j = n-1 initially
MatrixChainMultiplication(mat[], low , high):
    // 0 steps are required if low equals high 
    // case of only 1 sized sub-problem.
    If(low=high):
        return 0
            
    // Initialize minCost to a very big number. 
    minCost = Infinity
    
    // Iterate from k = low to k = high-1
    For(k=low to high-1):
        /* 
         Cost = Cost of Multiplying chain on left side +
                Cost of Multiplying chain on right side +
                Cost of Multiplying matrix obtained from left 
                and right side.
        */
        cost=MatrixChainMultiplication(mat, low, k)+
            MatrixChainMultiplication(mat, low+1, high)+
            mat[low-1]*mat[k]*mat[high]
            
        // Update the minCost if cost<minCost.
        If(cost<minCost):
            minCost=cost
            
    return minCost

Explanation – To implement the matrix chain multiplication algorithm we can have a recursive function MatrixChainMultiplication which accepts three arguments i.e.i.e. an array (say mat) of integers representing dimensions of the matrices, low representing the starting index of the current sub-problem (initially low will be 0), and high representing the last index of the current sub-problem.

• The base case of this recursive function occurs when we will reach low$=$high because it means we are left with a sub-problem of size 1 $i.e.$ a single matrix $M_i$ so we will return 0.
• Then, we will iterate from low to high and place parentheses for each i such that low$\le i<$high.
• During each iteration we will also calculate the cost incurred if we place at that particular position $i.e.$ Cost of left sub-problem + cost of right sub-problem + mat[low-1]$\times$_mat[k]$\times$_mat[high]
• At last we will return the minimum of the costs found during the iteration.

C/C++ Implementation of Recursive Approach

#include<bits/stdc++.h>
using namespace std;
// Function to find the minimum number of Multiplication
//  steps required in multiplying a chain of n matrices.

int MatrixChainMultiplication(int mat[],int low, int high){
    // If we are left with one matrix then 
    // we don't need any multiplication steps.
    if(low==high)
        return 0;
    
    // Initializing minCost with very 
    // large value.
    int minCost=INT_MAX;
    
    // Iterating from low to high - 1
    for(int k=low;k<high;k++){
        /* 
         Cost = Cost of Multiplying chain on left side +
                Cost of Multiplying chain on right side +
                Cost of Multiplying matrix obtained from left 
                and right side.
        */
        int cost=MatrixChainMultiplication(mat, low, k)+
            MatrixChainMultiplication(mat, k+1, high)+
            mat[low-1]*mat[k]*mat[high];
        
        // If the above cost is less than 
        // minCost find so far then update minCost.
        if(cost<minCost)
            minCost=cost;
    }
    // Returning the minCost
    return minCost;
}
// Main Function 
int main(){
    // This matrix chain of length 5 represents 
    // 4 matrices of dimensions as follows - 
    // 2*4, 4*6, 6*8, and 8*6.
    int mat[]={2, 4, 6, 8, 6};
    int n=sizeof(mat)/sizeof(mat[0]);

    cout<<"Minimum number of steps are - ";
    cout<<MatrixChainMultiplication(mat, 1, n-1);
    return 0;
}

Java Implementation of Recursive Approach

public class Main{
    // Function to find the minimum number of Multiplication
    //  steps required in multiplying chain of n matrices.
    private static int MatrixChainMultiplication(int mat[],
                                        int low, int high){
        // If we are left with one matrix then 
        // we don't need any multiplication steps.
        if(low==high)
            return 0;
        
        // Initializing minCost with very 
        // large value.
        int minCost=Integer.MAX_VALUE;
        
        // Iterating from low to high - 1
        for(int k=low;k<high;k++){
            /* 
             Cost = Cost of Multiplying chain on left side +
                    Cost of Multiplying chain on right side +
                    Cost of Multiplying matrix obtained from left 
                    and right side.
            */
            int cost=MatrixChainMultiplication(mat, low, k)+
                MatrixChainMultiplication(mat, k+1, high)+
                mat[low-1]*mat[k]*mat[high];
            
            // If the above cost is less than 
            // minCost find so far then update minCost.
            if(cost<minCost)
                minCost=cost;
        }
        // Returning the minCost
        return minCost;
    }
    // Main Function 
    public static void main(String args[]){
        // This matrix chain of length 5 represents 
        // 4 matrices of dimensions as follows - 
        // 2*4, 4*6, 6*8, and 8*6.
        int mat[]={2, 4, 6, 8, 6};
        int n=mat.length;
        
        System.out.println("Minimum number of steps are - "+
                        MatrixChainMultiplication(mat, 1, n-1));
    }
}

Output –

Minimum number of steps are - 240

Complexity Analysis

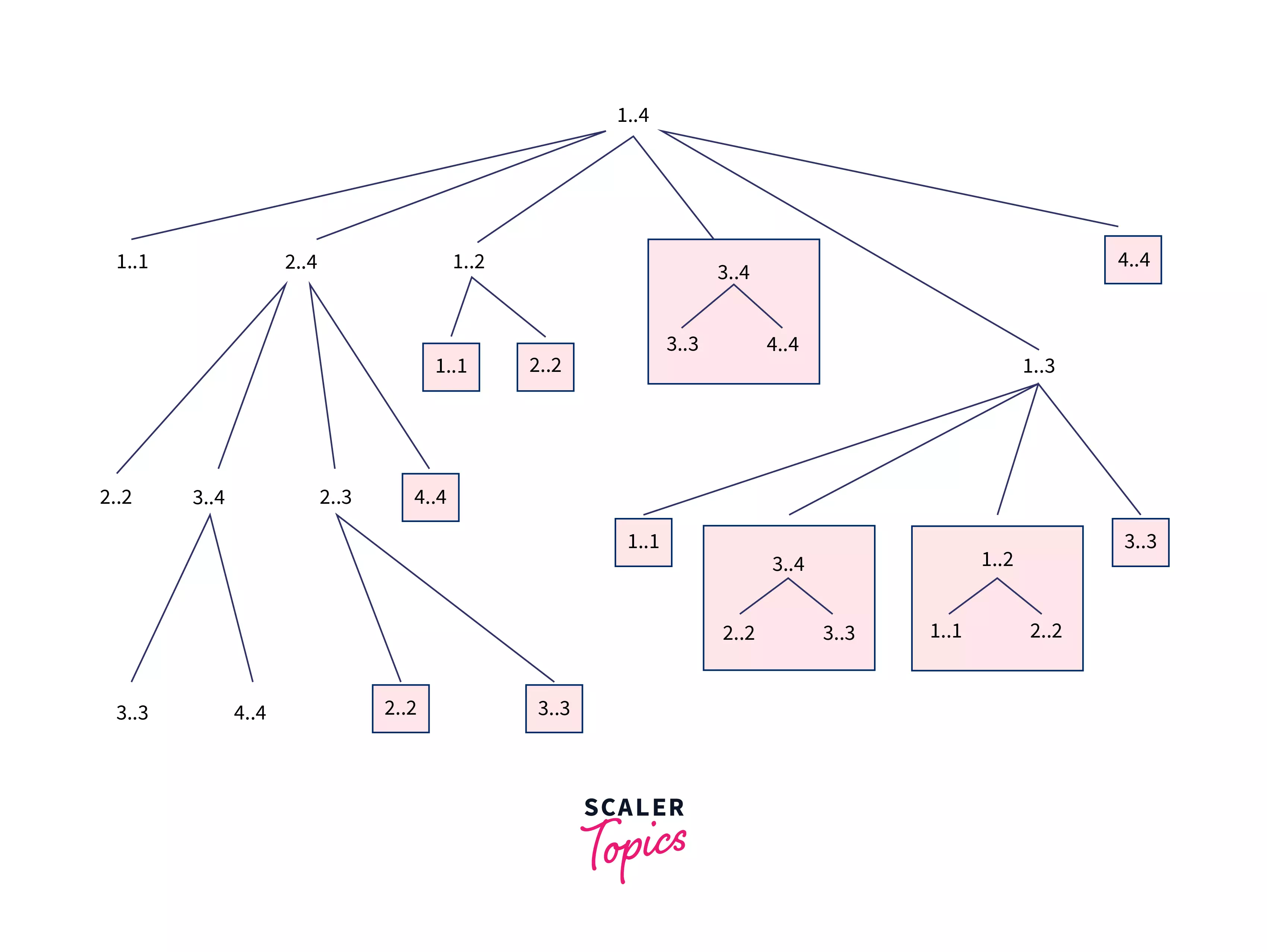
• Time Complexity –
  Let $T(n)$ be the total number of ways to place parentheses in the matrix chain, where $T(n)$ is defined as –
  $$T(n)=\{\begin{array}{lll}{\mathrm{\Sigma }}_{i=1}^{n-1}T(i)+T(n-i),& \text{if }n\ge 21,& \text{if }n=1\end{array}$$ On solving the above given recurrence relation, we get – $T(n)=O(2^n)$ which grows at an exponential rate.
• Space Complexity –
  Though we have not used any auxiliary space but as you can see in the above image, the maximum depth of the recursive tree can reach up to $O(n)$ where $n$ is the length of the matrix chain.
  Hence the overall space complexity is $O(n)$

Need of Dynamic Programming

If we closely observe the recursive tree that is formed during finding the multiplication order, we will find that the result of the same sub-problem had been calculated many times also many overlapping sub-problems can be seen in the recursive tree.

For example, in a matrix chain of length 4, the recursive tree formed looks like –

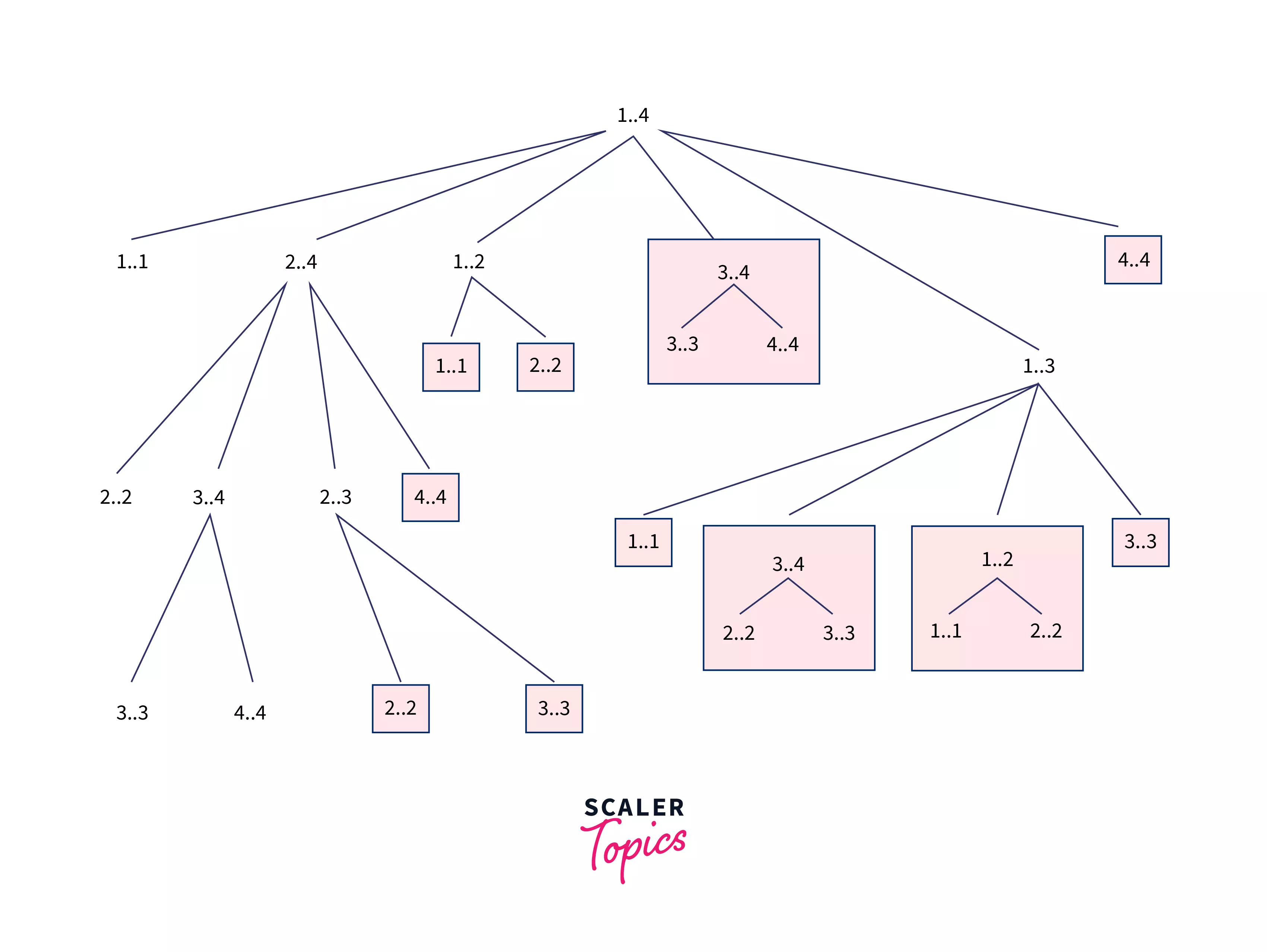
We can see that answers for the sub-problem $1..2$, and $2..3$ have been calculated two times. So if we store them somewhere it will highly beneficial to speed up the process.

All these things suggest using Dynamic programming to find an efficient solution.

DP With Memoization

Algorithm for DP Using Memoization

The algorithm is almost the same as the naive recursive solution with the only change that here we will use a $dp$ array of dimension $n\times n$.

Steps –

• Declare a global $dp$ array of dimension $n\times n$ and initialize all the cells with value $-1$.
• $dp[i][j]$ holds the answer for the sub-problem $i..j$ and whenever we will need to calculate $i..j$ we would simply return the stored answer instead of calculating it again.
• Initialize variables low with $1$, and high with $n-1$ and call the function to find the answer to this problem.
• If $low=high$ then return 0 because we don’t need any step to solve sub-problem with a single matrix.
• If $dp[low][high]\ne -1$ it means the answer for this problem has already been calculated. So we will simply return $dp[low][high]$ instead of solving it again.
• In the other case, for each $i=low$ to $i=high-1,$ we will find the minimum number of steps in solving the left sub-problem, right sub-problem, and steps required in multiplying the result obtained from both sides.
  Store the result obtained in dp[low][high] and return it.
• At last answer for $low=0$ and $high=n-1$ $i.e.$ $dp[0][n-1]$ will be returned.

Pseudocode

// mat = Matrix chain of length n
n=mat.length;
// Initialize dp array of dimension n*n
// all of it's entries initialize with -1. 
dp[n][n]
MatrixChainMultiplication(mat[], low, high):
    // 0 steps are required if low equals high 
    // case of only 1 sized sub-problem.
    if(low==high):
        return 0
    // If dp[low][high] is not -1 then, it means 
    // answer for sub-problem low...high has already 
    // been calculated.
    if(dp[low][high]!=-1):
        return dp[low][high];
    
    // Else initialize dp[low][high] with infinity.
    dp[low][high] = infinity
    
    // Iterate from i = low to i = high-1
    For(i=low To high-1):
        // Compute the cost if we place parentheses 
        // here. 
        cost = MatrixChainMultiplication(mat, low, k)+
            MatrixChainMultiplication(mat, i+1, high)+
            mat[low-1]*mat[i]*mat[high]
            
        // Update the dp[low][high] if cost<dp[low][high].
        dp[low][high] = min(dp[low][high], cost)
    
    return dp[low][high]

Explanation – We will use almost the same approach as Recursive Implementation with the only change that, we will maintain a 2-D array (say dp) of dimensions n×n all of whose entries initialized with -1 where dp[i][j] stores result for the sub-problem i..j.

So for calculating the answer for the sub-problem i..j firstly we will check if we already have calculated the answer for it in past, by checking that if dp[i][j]!=-1. So if we already have calculated the answer for it we need not solve it again instead, we can simply return dp[i][j]

C/C++ Implementation

#include<bits/stdc++.h>
using namespace std;

int **dp;
// Function to find the minimum number of Multiplication
//  steps required in multiplying a chain of n matrices.

int MatrixChainMultiplication(int mat[],int low, int high){
    // If we are left with one matrix then 
    // we don't need any multiplication step.
    if(low==high)
        return 0;
        
    // If dp[low][high]!=-1 it means, 
    // we already have solved this sub-problem.
    // So we will instantly return it.
    if(dp[low][high]!=-1)
        return dp[low][high];
    
    // Initializing dp[low][high] with very 
    // large value.
    dp[low][high]=INT_MAX;
    
    // Iterating from low to high - 1
    for(int k=low;k<high;k++){
        /* 
         Cost = Cost of Multiplying chain on left side +
                Cost of Multiplying chain on right side +
                Cost of Multiplying matrix obtained from left 
                and right side.
        */
        int cost=MatrixChainMultiplication(mat, low, k)+
            MatrixChainMultiplication(mat, k+1, high)+
            mat[low-1]*mat[k]*mat[high];
        
        // If the above cost is less than dp[low][high]
        // find so far then update dp[low][high].
        if(cost<dp[low][high])
            dp[low][high]=cost;
    }
    // Returning the value dp[low][high], 
    // since initially low=1, and high=n-1
    // therefore at last dp[1][n-1] will be returned.
    return dp[low][high];
}
// Main Function 
int main(){
    // This matrix chain of length 5 represents 
    // 4 matrices of dimensions as follows - 
    // 2*4, 4*6, 6*8, and 8*6.
    int mat[]={2, 4, 6, 8, 6};
    int n=sizeof(mat)/sizeof(mat[0]);
    
    // Assigning memory to dp array 
    // and Initializing with -1.
    dp=new int*[n];
    for(int i=0;i<n;i++){
        dp[i]=new int[n];
        for(int j=0;j<n;j++)
            dp[i][j]=-1;
    }
    cout<<"Minimum number of steps are - ";
    cout<<MatrixChainMultiplication(mat, 1, n-1);
    return 0;
}

Output –

Minimum number of steps are - 240

Complexity Analysis

• Time Complexity – In the function we are iterating from $1$ to $n-1$ which costs $O(n)$ and in each iteration, it takes $O(n^2)$ time to calculate the answer of left and right sub-problems.
  Hence, the overall time complexity is $O(n^3)$
• Space Complexity – We are using $dp$ array of dimension $n\times n$. So the space complexity is $O(n^2)$

Bottom-up DP Solution

Algorithm

To solve this problem in a Bottom-up manner we will be following the “Gap strategy”. Gap strategy means firstly we will solve all the sub-problems with gap=0, then with gap=1, and at last problem with gap=n-2.

For solving a problem with gap $i$ such that $i\ge 2$, all the problems of size $i-1$ will be taken into account. Please refer to the following algorithm and example for a better understanding.

• For sub-problem with gap 0 (single matrix), no multiplication is required so the answer will be 0.
• For sub-problem with gap 1 (two matrices $i.e.$ A and B) the only option is to simply find steps required in multiplying A and B.
• For sub-problems with gap$\ge 2$ we need to find the minimum by placing the brackets at all the possible places.

For example –

• Answer for the sub-problem $i,j$, when $i=j$ is 0.
• Answer for the sub-problem $i,j$, when $j-i=1$ is $mat[i]\times$ $mat[j]\times mat[j+1]$.
• Answer for the sub-problem $i,j$, when $(j-i)\ge 2$, is obtained by placing bracket at all possible places, and then calculating the sum of left sub-problem, right sub-problem and cost of multiplying matrices obtained from left and right side.

Pseudocode

n=mat.length;
// Declare a dp array of dimensions 
// (n-1)*(n-1).
dp[n-1][n-1]
MatrixChainMultiplication(mat[], n):
    // Iterate from gap = 0 to gap = n-2 
    For(gap=0 To n-2):
        // Initialize i with 0 and j with 
        // gap and iterate till j = n-2 
        For(i=0, j=gap To j=n-2):
            // If gap is 0, then no multiplication 
            // steps are required. 
            If(gap=0):
                dp[i][j]=0
            // If gap is 1, we don't have any choice other 
            // than multiplying them directly.
            Else If(gap=1):
                dp[i][j]=mat[i]*
                        mat[j]*mat[j+1]
            // Else if gap >= 2
            Else:
                // Initialize minCost with infinity 
                // (A very large number say INT_MAX)
                minCost=infinity
                
                // Iterate from k = i to k = j-1
                For(k=i To k=j-1):
                    // Compute left, right and mergeCost
                    leftCost = dp[i][k]
                    rightCost = dp[k+1][j]
                    mergeCost = mat[i]*
                            mat[k+1]*mat[j+1]
                    // If sum of leftCost, rightCost and mergeCost
                    // is smaller than minCost then update it.
                    minCost=min{minCost, 
                        leftCost+rightCost+mergeCost}
                // Assign minCost to dp[i][j].              
                dp[i][j]=minCost
                
    return dp[0][n-2]

Let’s dry run this algorithm on $mat=2,4,6,8,6$.

Here the length of the chain is 5, so we will create $dp$ array of dimension $4\times 4$ as shown below –

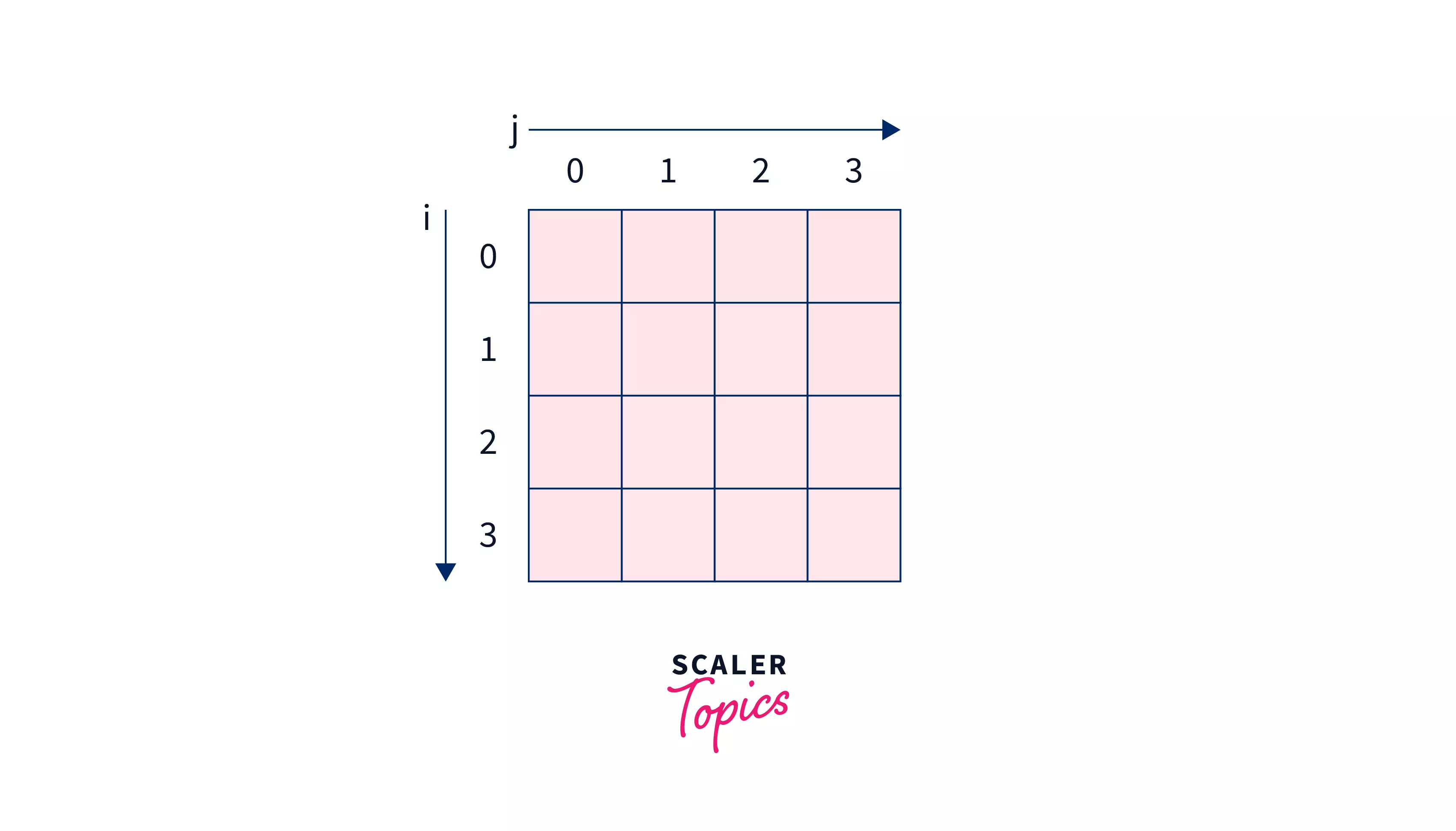
Then solving sub-problems of size $0$ $i.e.$ $0,0,$ $1,1,$ $2,2,$ and $3,3$. As per the algorithm all of them will result in 0.
After which $dp$ array will look like –

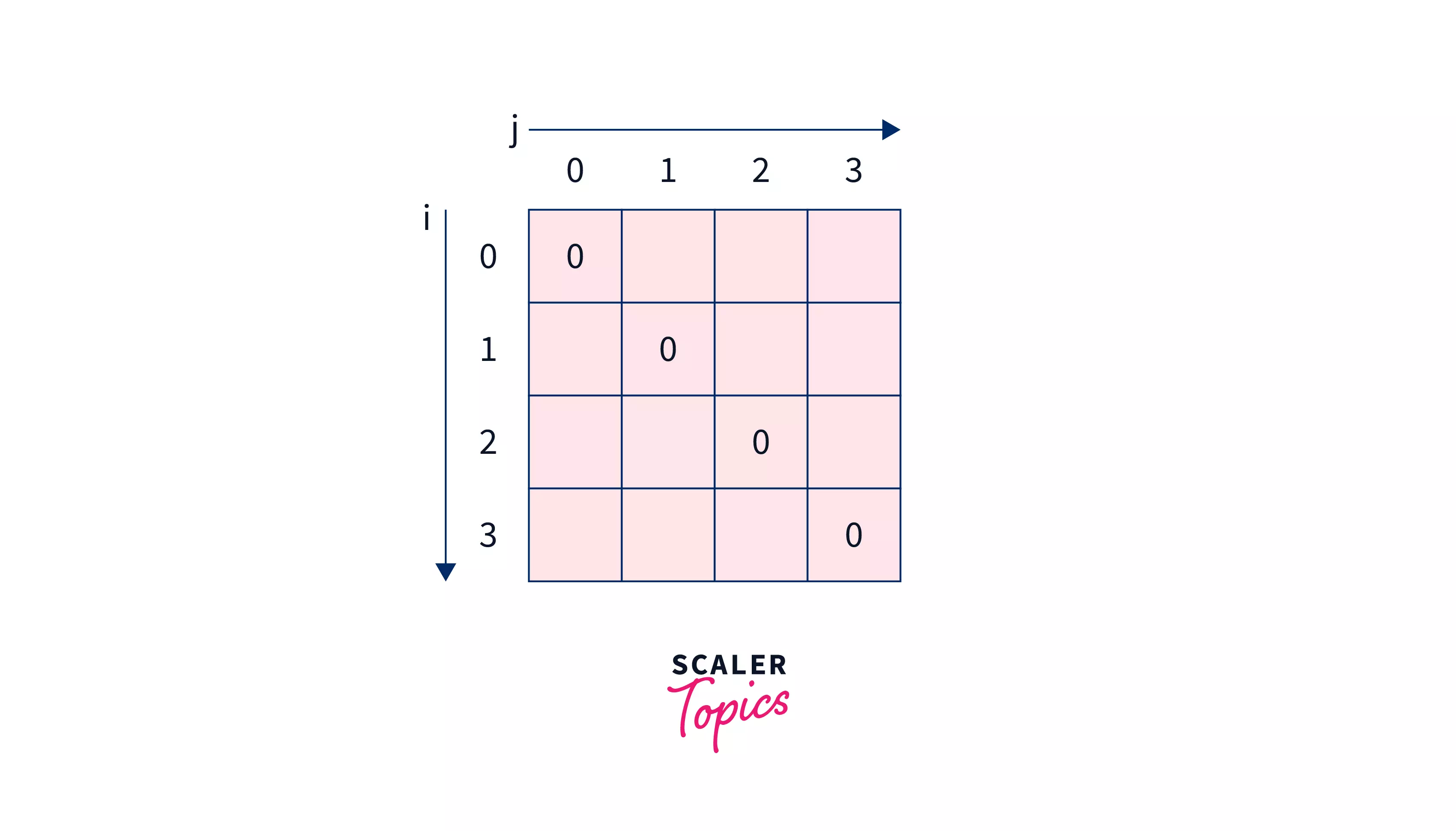
Solving all sub-problems of gap $1$ $i.e.$ $0,1,$ $1,2,$ and $2,3,$.

• $0,1$ will result in $2\times 4\times 6$ $=48$
• $1,2$ will result in $4\times 6\times 8$ $=192$
• $2,3$ will result in $6\times 8\times 6$ $=288$

After which $dp$ array will look like –

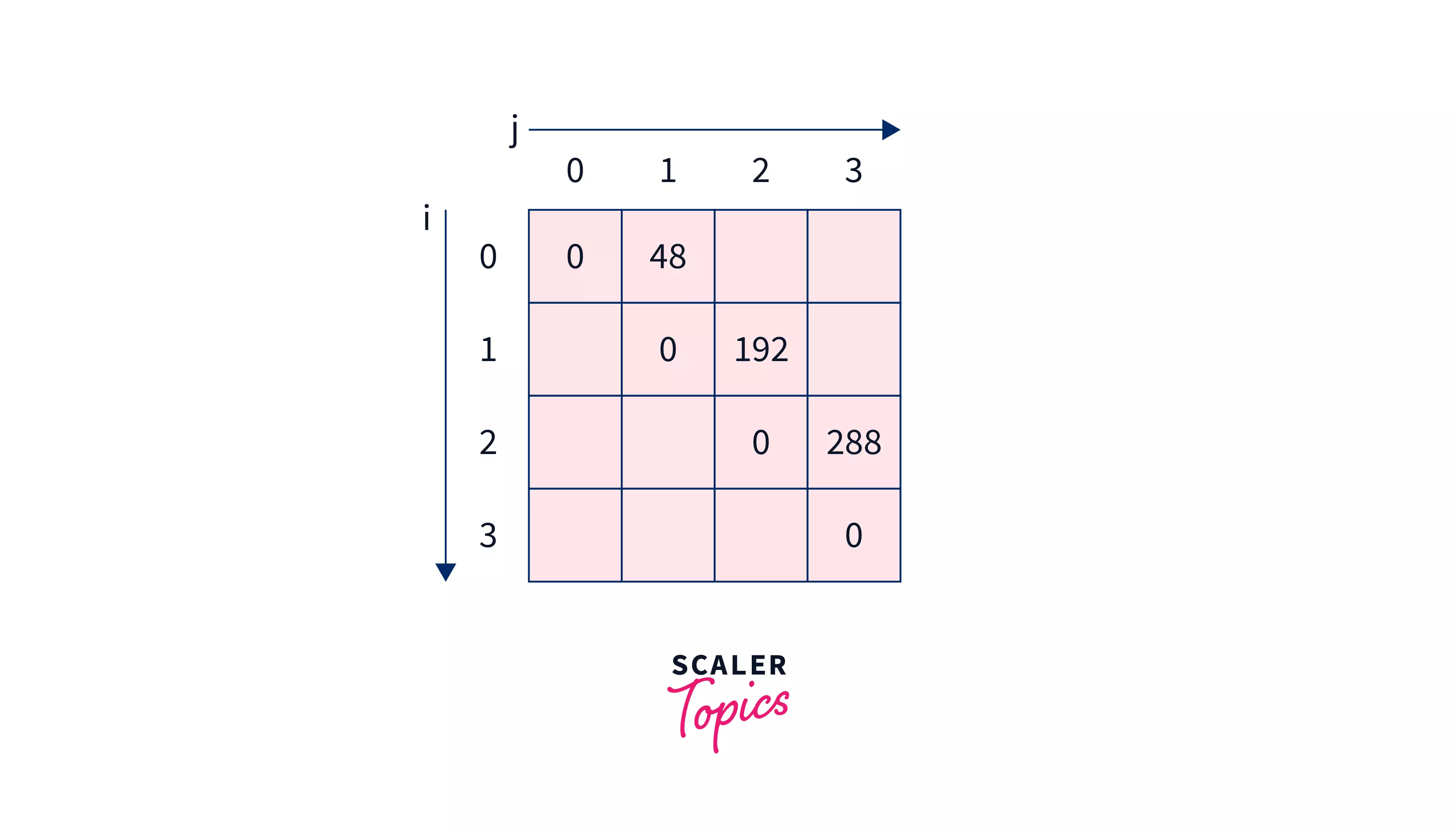
Now solving sub-problems with gap $2$ $i.e.$ $0,2$ and $1,3$.

• $0,2$ will result in minimum of –
  • $dp[0][0]+dp[1][2]+(2\times 4\times 8)=0+192+64=256$
  • $dp[0][1]+dp[2][2]+(2\times 6\times 8)=48+0+96=144$
  Hence we will make $dp[0][2]$ as $144$.
• $1,3$ will result in minimum of –
  • $dp[1][1]+dp[2][3]+(4\times 6\times 6)=0+288+144=432$
  • $dp[1][2]+dp[2][2]+(4\times 8\times 6)=192+0+192=384$
  Hence we will make $dp[1][3]$ as $384$

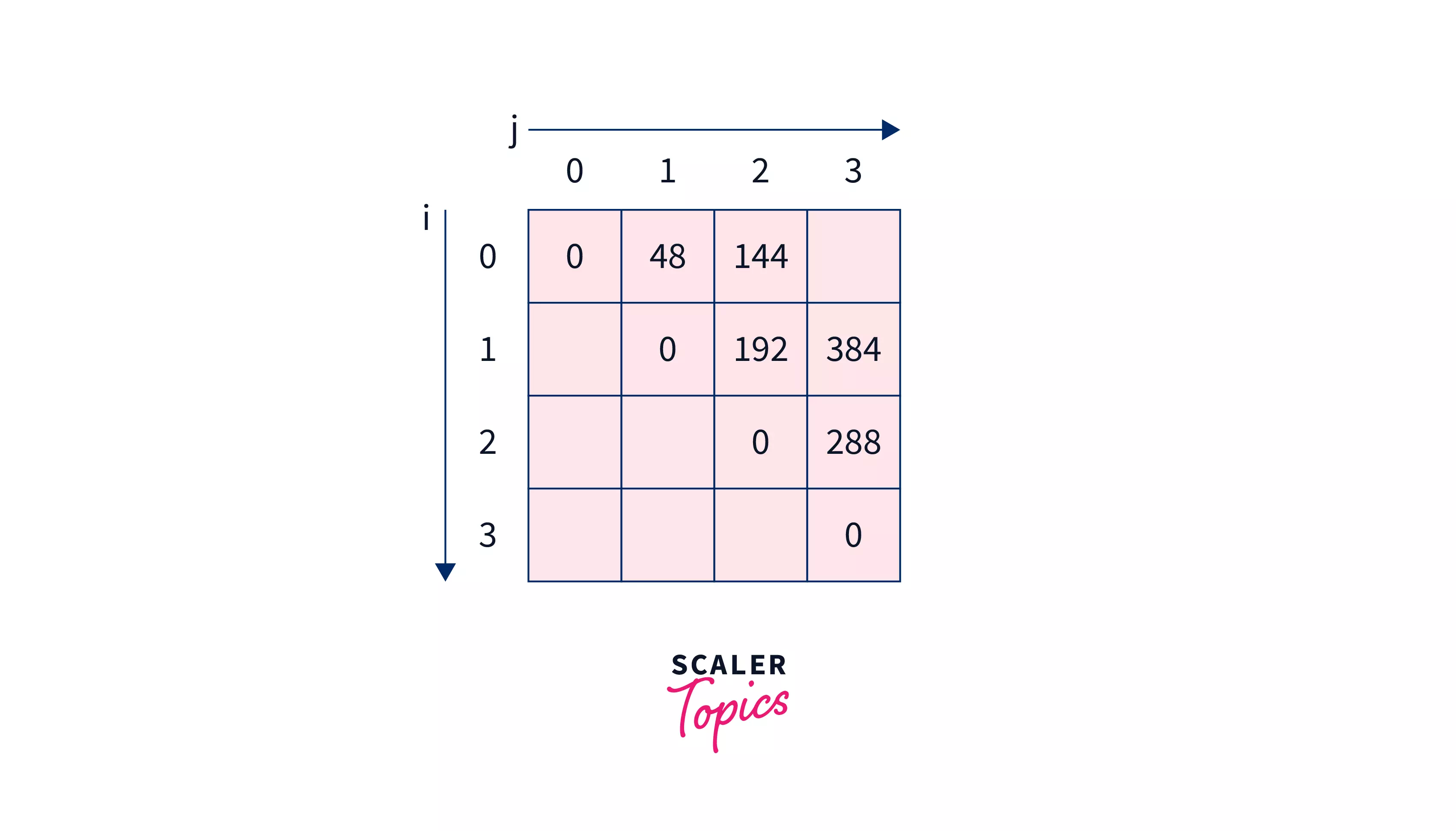
Now solving the last problem (main problem) with gap 3 $i.e.$ $0,3$. It will be minimum of –

• $dp[0][0]+dp[1][3]+(2\times 4\times 6)=0+384+48=432$
• $dp[0][1]+dp[2][3]+(2\times 6\times 6)=48+288+72=408$
• $dp[0][2]+dp[3][3]+(2\times 8\times 6)=144+0+96=240$

So 240 is the minimum among them, hence we will make $dp[0][3]$ as 240 making $dp$ array look like –

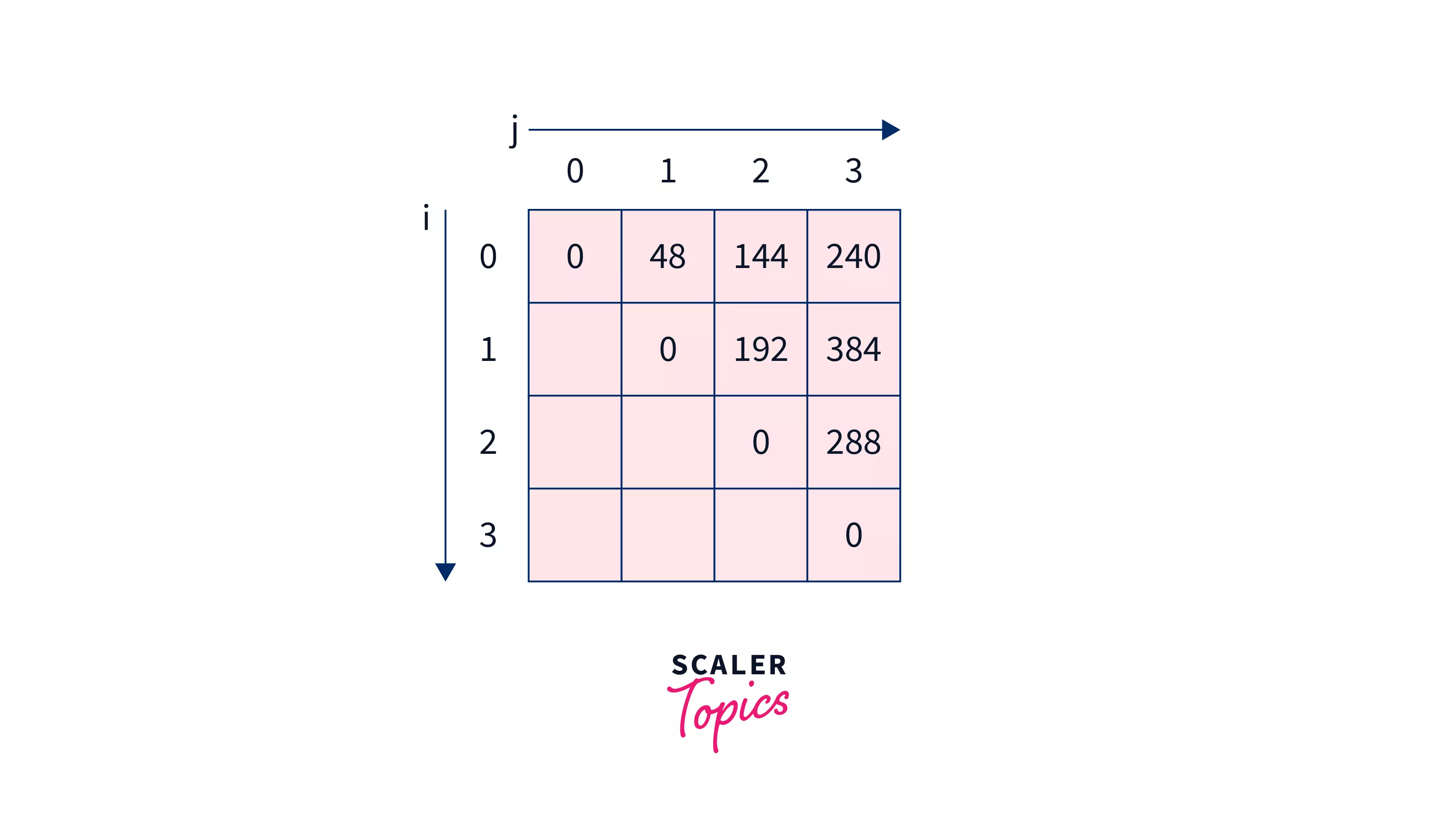
At last we will return $dp[0][5-2]=dp[0][3]$ $i.e.$ $240$.

C/C++ Implementation

We will use a 2-D array (say $dp$) of dimensions $(n-1)\times (n-1)$ because the last problem is of size/gap $n-2$.
Then we will iterate for each sub-problem with gap/size $0$ till the last problem with gap/size $n-2$ and compute the answer for the sub-problem based on the rules discussed in the algorithm section. At last, the answer of the final problem will be stored in $dp[0][n-2]$ so we will simply return it.

#include<bits/stdc++.h>
using namespace std;

// Function to find the minimum number of Multiplication
//  steps required in multiplying chain of n matrices.
int MatrixChainMultiplication(int mat[],int n){
    // Making 2d DP array of dimensions 
    // (n-1)*(n-1)
    int dp[n-1][n-1];
    
    // Iterating while gap between first 
    // length vary from 0 to n-1.
    for(int gap=0;gap<n-1;gap++){
        // Starting i from 0 and j=gap.
        // Iterating till j<n-1. 
        for(int i=0,j=gap;j<n-1;i++,j++){
            // If gap is 0 (single matrix)
            // then assigning 0 to dp[i][j].
            if(gap==0)
                dp[i][j]=0;
            // Else if the gap is (2 matrices)
            // i.e. only once choice (mat1*mat2)
            else if(gap==1){
                dp[i][j]=mat[i]*mat[j]*mat[j+1];
            }
            // Else if gap>1, then we need to 
            // find the optimal method. 
            else{
                // Initializing minCost with very large value.
                int minCost=INT_MAX;
                
                // Iterating from k=i to 
                // k = j-1 and finding cost.
                /* 
                 Cost = Cost of Multiplying chain on left side +
                        Cost of Multiplying chain on right side +
                        Cost of Multiplying matrix obtained from left 
                        and right side.
                */
                for(int k=i;k<j;k++){
                    int leftCost=dp[i][k];
                    int rightCost=dp[k+1][j];
                    int thisCost=mat[i]*mat[k+1]*mat[j+1];
                    
                    minCost=min(minCost,leftCost
                            +rightCost+thisCost);
                }
                // Assigning minCost find to dp[i][j].
                dp[i][j]=minCost;
            }
        }
    }
    // Returning dp[0][n-2].
    return dp[0][n-2];
}
// Main Function 
int main(){
    // This matrix chain of length 5 represents 
    // 4 matrices of dimensions as follows - 
    // 2*4, 4*6, 6*8, and 8*6.
    int mat[]={2, 4, 6, 8, 6};
    int n=sizeof(mat)/sizeof(mat[0]);
    
    cout<<"Minimum number of steps are - ";
    cout<<MatrixChainMultiplication(mat, n);
    return 0;
}

Output –

Minimum number of steps are - 240

Complexity Analysis

• Time Complexity – We are using three nested for loops, each of which is iterating roughly $O(n)$ times. Hence, the overall time complexity is $O(n^3)$.
• Space Complexity – We are using an auxiliary $dp$ array of dimensions, $(n-1)\times (n-1)$ hence space complexity is $O(n^2)$

Join our expert-led Free Dynamic Programming Course to master advanced problem-solving techniques and enhance your programming prowess.

Conclusion

• In the matrix chain multiplication problem, the minimum number of multiplication steps required to multiply a chain of matrices has been calculated.
• Determining the minimum number of steps required in the matrix chain multiplication can highly speed up the multiplication process.
• It takes $O(n^3)$ time and $O(n^2)$ auxiliarly space to calculate the minimum number of steps required to multiply a chain of matrices using the dynamic programming method.
• It is very important to decide the order of multiplication of matrices in matrix chain multiplication to perform the task efficiently.
• So the minimum number of multiplication steps required to multiply a chain matrix in matrix chain multiplication of length $n$ has been computed.
• Trying out all the possibilities recursively is very time consuming hence the method of dynamic programming is used to find the same.
• The minimum number of steps required to multiply a chain of matrices in matrix chain multiplication can be found in $O(n^3)$ time complexity using dynamic programming.