Matrix Multiplication in C

Introduction to Matrix Multiplication in C

An ordered rectangular array of numbers or functions is known as a matrix. A rectangular array of m x n numbers in the form of n vertical lines called columns and m horizontal lines called rows is called a matrix of order m by n.

Two matrices can be multiplied only if the number of columns in the first matrix equals the number of rows in the second matrix. The product of the two matrices will have the order of the number of rows in the first row and the number of columns in the second matrix.

The product of two matrices, A and B, is the sum of the products across some row of A with the corresponding entries down some column of B. In simple words, The dot product of the first row of the first matrix and the first column of the second matrix will result in the first element of the product matrix.

This can be understood easily by the following illustration.

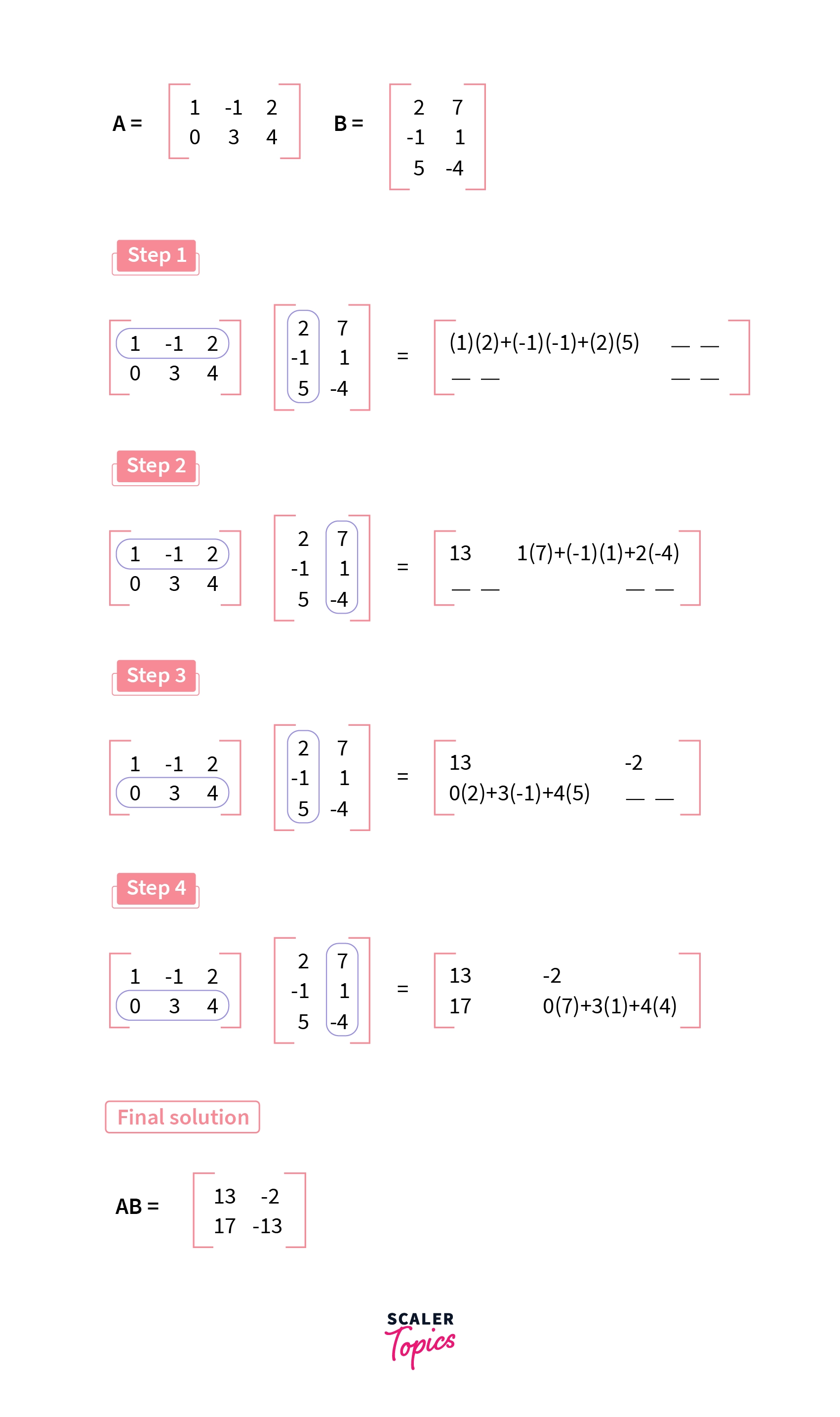
Algorithm of C Programming Matrix Multiplication

1. Start.
2. Enter the value of m and n (or) order of the first matrix.
3. Enter the value of p and q (or) order of the second matrix.
4. Create a matrix of size a[m][n] and b[p][q].
5. Enter the element of matrices row-wise using loops.
6. If the number of columns of the first matrix is not equal to the number of rows of the second matrix, print matrix multiplication is not possible and exit. If not, proceed to the next step.
7. Create a third matrix, c of size m x q, to store the product.
8. Set a loop from i=0 to i=m.
9. Set an inner loop for the above loop from j=0 to j=q.
10. Initialise the value of the element (i, j) of the new matrix to 0.
11. Set an inner loop inside the above loop from k=0 to k=p.
12. Using the add and assign operator (+=) store the value of a[i][k] * b[k][j] in the third matrix, c[i][j].
13. Print the third matrix.
14. Stop.

Flow Chart of Matrix Multiplication

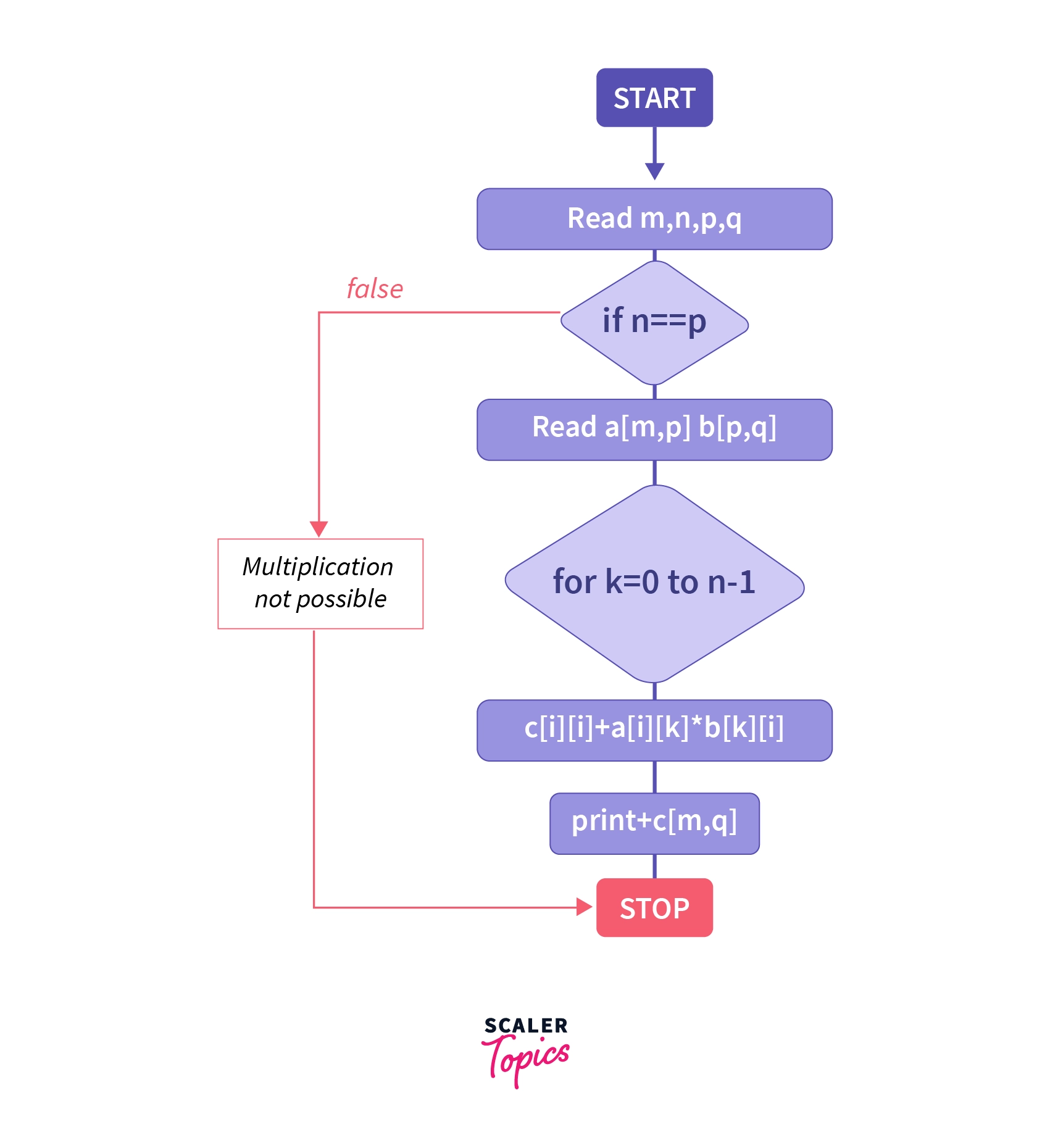
Multiplication of Two Matrices in C

There are mainly two types of matrices:

• Square matrix
• Rectangle matrix

Let's first start with square matrix multiplication.

Multiplication of Square Matrices

A matrix in which the number of rows equals the number of columns is called a square matrix. Multiplication of two square matrices of the same order is possible only when both the matrices have the same order.

To calculate the product of the two matrices, we multiply the corresponding elements and add the products together. It can be understood even better with the illustration which was mentioned under the heading introduction to matrix multiplication in C.

Given below is the code to find the product of two square matrices.

Notice that in the above program, we asked the user to enter the order of the matrix only once. It is because the multiplication of two square matrices of a different order is not possible.

output

Multiplication of Rectangular Matrices

A matrix in which the number of rows is not equal to the number of columns is called a rectangular matrix.

The criteria for the compatibility of multiplication of two rectangular matrices remains the same as the criteria for multiplication of two square matrices, i.e, the number of columns in the first matrix should be equal to the number of rows in the second matrix.

Given below is a code to find the product of two rectangular matrices.

When the number of columns in the first matrix is equal to the number of rows in the second matrix.

output

Let us try running the program with the number of columns in the first matrix not equal to the number of rows in the second matrix.

output

Multiply Matrices by Passing it to a Function

So far, in our journey of matrix multiplication in C. We have seen a multiplication of two square matrices and two rectangular matrices. By now, you would have an idea about how long the codes are for taking the input of the matrix, displaying the matrix, and multiplication of the matrix. Imagine in a program you need to perform the multiplication of matrices 10 times. The same code has to be written 10 times.

Debugging the program becomes really difficult and messy, and also writing the same code 10 times will increase the size of the program and increase the compilation time. At the end of the day, a good code is the one that takes less space and takes less time to execute. To overcome these problems, we can make use of the functions.

We will now learn how to perform matrix multiplication by passing it to a function. We will need mainly 3 functions. One to take the matrix as input, let’s name this the input() function. We will also need a function to display the result of the matrix, and we’ll name it the display() function. Finally, we will need a function to calculate the product of the two matrices, and let's name this as multiply().

The input() function will take the elements of the matrix as input.

Here is the code for input() function.

Now let us look at the function to display the matrix. We will make use of the display() function to print the matrix.

The code for display() function is as follows:

To find the product of two matrices, we can make use of the multiply() function.

The code for the multiplication of two matrices is as follows:

Benefits of C Programming Matrix Multiplication

• Matrix multiplication in C eases out the tedious manual work of finding the product of two matrices.
• Matrix multiplication in C helps us to learn the application of mathematical logic into a coding algorithm.
• Matrix multiplication in C also helps us to find the solutions to linear equations easily.