Matrix Multiplication in Java

Introduction

You might have learned about multiplying two matrices in Linear Algebra before. Say we have two matrices and we try to multiply these using an algorithm that you can devise given some time.

First, let’s brush up on the fundamentals before we tackle the problem itself. To calculate the product we need to ensure two facts or else matrix multiplication is not possible. Let us assume we have two matrices A and B of dimensions $m\times n$ and $p\times q$ respectively.

1. The number of columns in the first matrix must be equal to the number of rows in the second matrix. This implies $n = p$ must hold true.
2. The resultant product has dimensions: number of rows in first matrix * number of columns in the second matrix. Thus the resultant matrix has the following dimension: $m\times q$.

Example

Multiplying A and B where the shape of A is 3 x 2 (meaning it has 3 rows and 2 columns) and the shape of B is 2 x 4 (meaning it has 2 rows and 4 columns) is possible because both the conditions mentioned above hold. If the shape of A was 3 x 3 and the shape of B was 2 x 4, the matrix multiplication would not be possible.

Let’s look at an example :

Here A = [{3, 4}, {2, 1}], B = [{1, 5}, {3, 7}]. The product of A and B is C. The C(i, j) entry in matrix C can be calculated as the dot product of row i of A and column j of B.

Example: C(1,1) = 3 * 1 + 4 * 3 = 15.

Mathematically, we can express the formula as:

where n = number of columns in the first matrix.

Key takeaway: To calculate the C(i, j) entry, we need to multiply the ith row values of A with the corresponding jth column values of B and sum them over.

Multiplication using For loops

As we’ve mentioned before, the C(i,j) entry is the dot product of row i of A and column j of B.

C(1,1) = dotProduct( row(A, 1), col(B, 1) ) = $3\times1$ + $4\times3$ = $15$

C(1,2) = dotProduct( row(A, 1), col(B, 2) ) = $3\times5$ + $4\times7$ = $43$

C(2,1) = dotProduct( row(A, 2), col(B, 1) ) = $2\times1$ + $1\times3$ = $5$

C(2,2) = dotProduct( row(A, 2), col(B, 2) ) = $2\times5$ + $1\times7$ = $17$

Let’s assume the shape of A is $n1\times n2$ and the shape of B is $n2\times n3$. Thus the shape of the resultant matrix would be $n1\times n3$.

If we would want to compute C(i, j) programmatically, we would need to iterate over the row i of A and column j of B (this will take O($n2$) steps because that is the number of columns in A). Since we need to calculate C(i,j) for all possible values of i and j, the total number of such computations would be $n1\times n3$.

Hence, the total time complexity is O(n1 * n2 * n3). Assuming n1 = n2 = n3 = n, the total time complexity is of the order of O($n^3$).

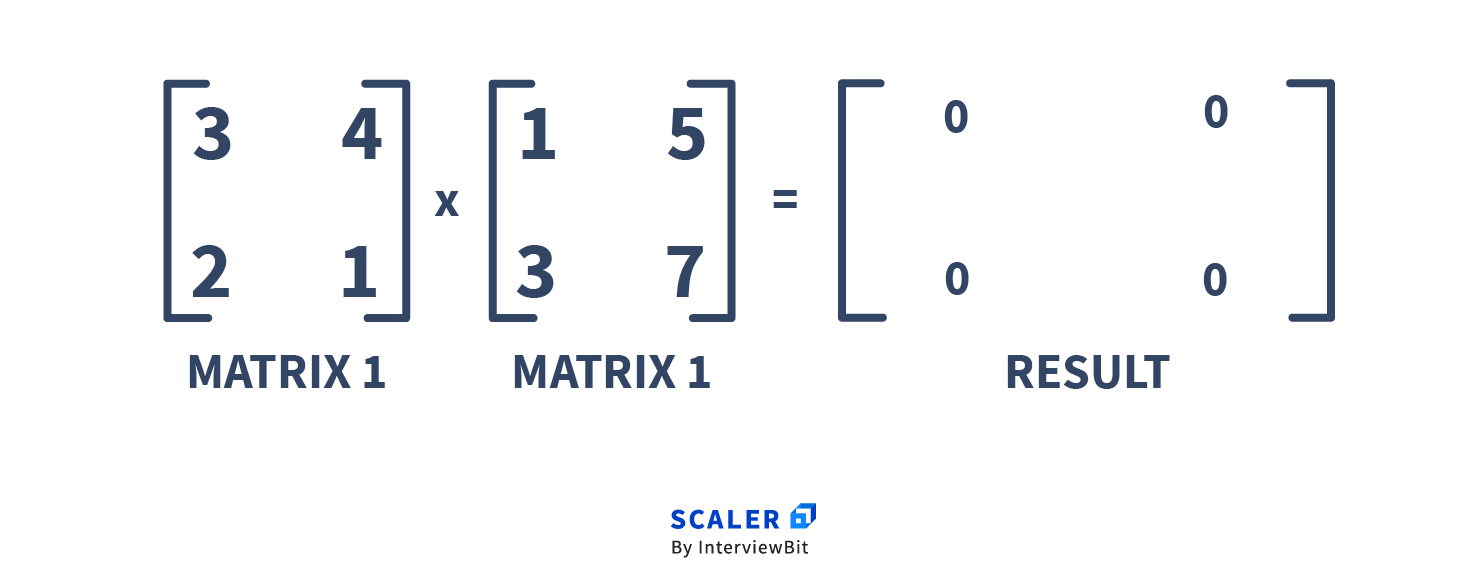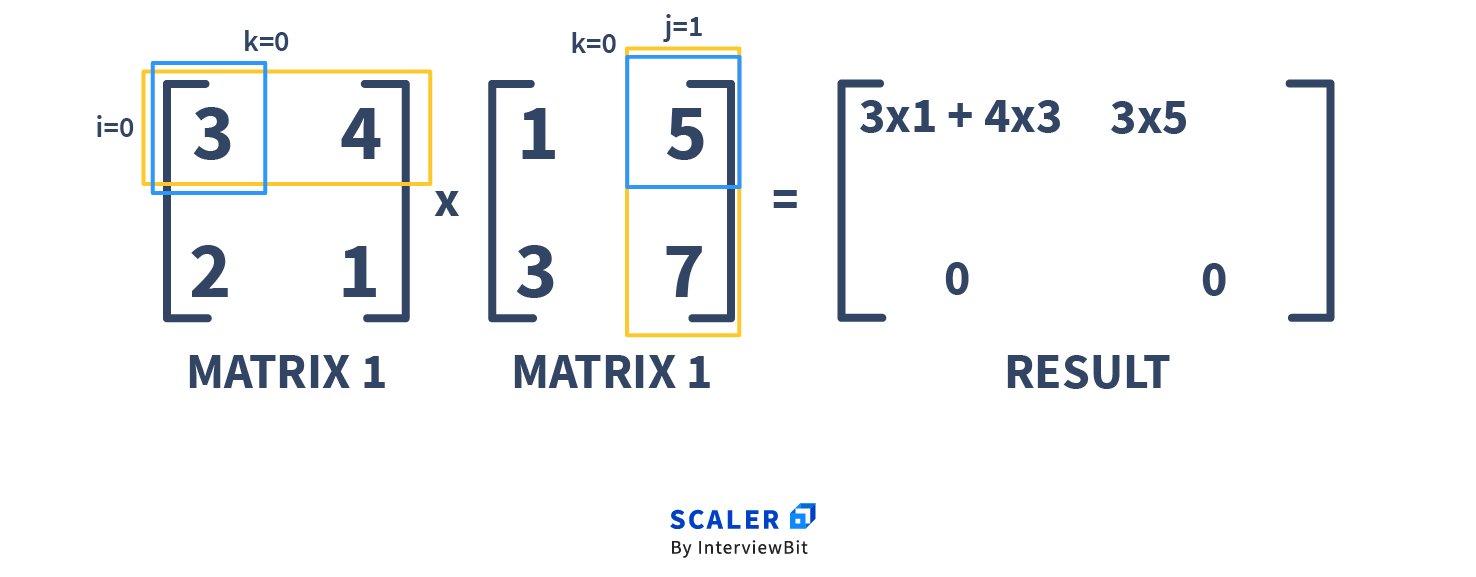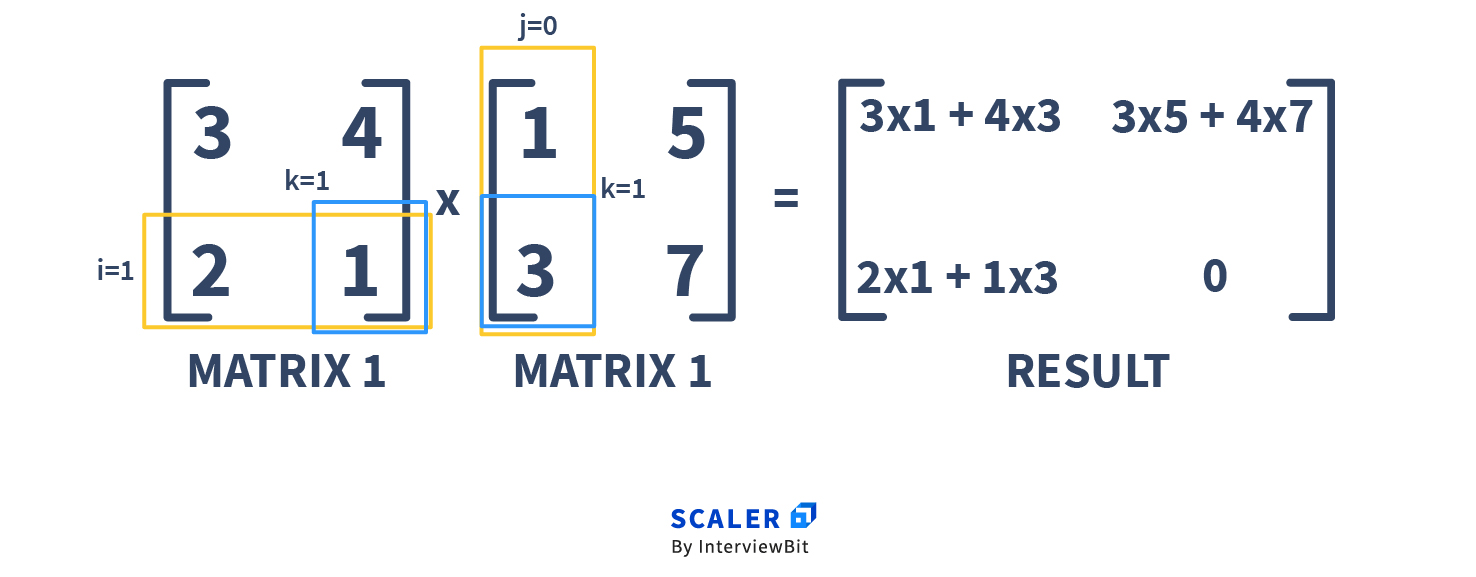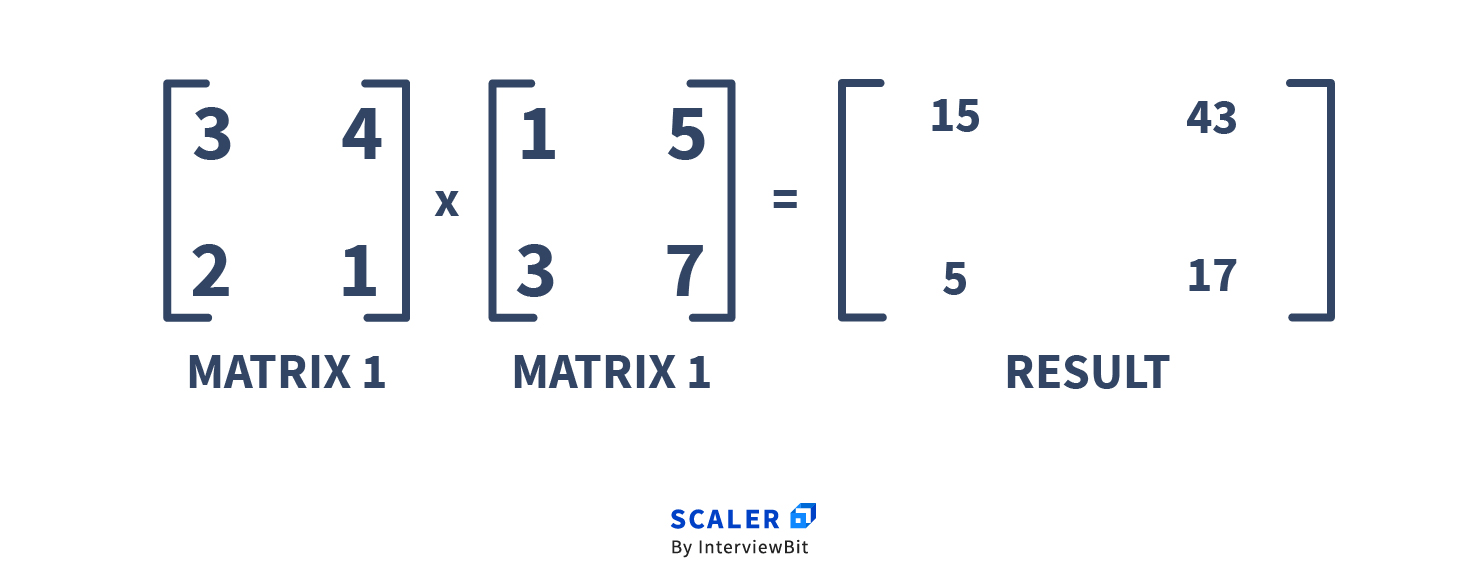
Now the question is: can we do better than $O(n^{3})$?

Sure, matrix multiplication time complexity can be reduced by using divide-and-conquer approach. It is called the Strassen Algorithm of matrix multiplication. The time complexity would be reduced to $O(n^{log7})$ which is approximately $O(n^{2.8})$.

Key takeaway: Matrix multiplication is a costly operation and naive matrix multiplication offers a time complexity of $O(n^{3})$. However, we can improve the time complexity of matrix multiplication to $O(n^{log7})$ by using Strassen Algorithm.

Example Program for Multiplication of Matrices in Java Using For Loop

Now that we’ve devised a way to visualize how to compute the entries in the product we can use the formula that we devised earlier to come up with a looped version of matrix multiplication. We use three loops:

• one to iterate over the rows of A
• second to iterate over the columns of B
• third to actually compute the dot product of these vectors.

Code:

Output:

Explanation:

• What we basically do in this program is first take the input dimensions of both matrices. If the number of columns in A is not equal to the number of rows in B we exit immediately.
• Else we take the inputs for A and B and create the result matrix C. All the values in the matrix are initialised to zero.
• Then, we iterate over the rows of A, columns of B and values of row/column to calculate matrix product respectively.