Merge K Sorted Arrays

Problem Statement

k number of arrays are given, the task is to merge all the given integer arrays in such a manner that the resultant array is sorted in the runtime only.

Example:

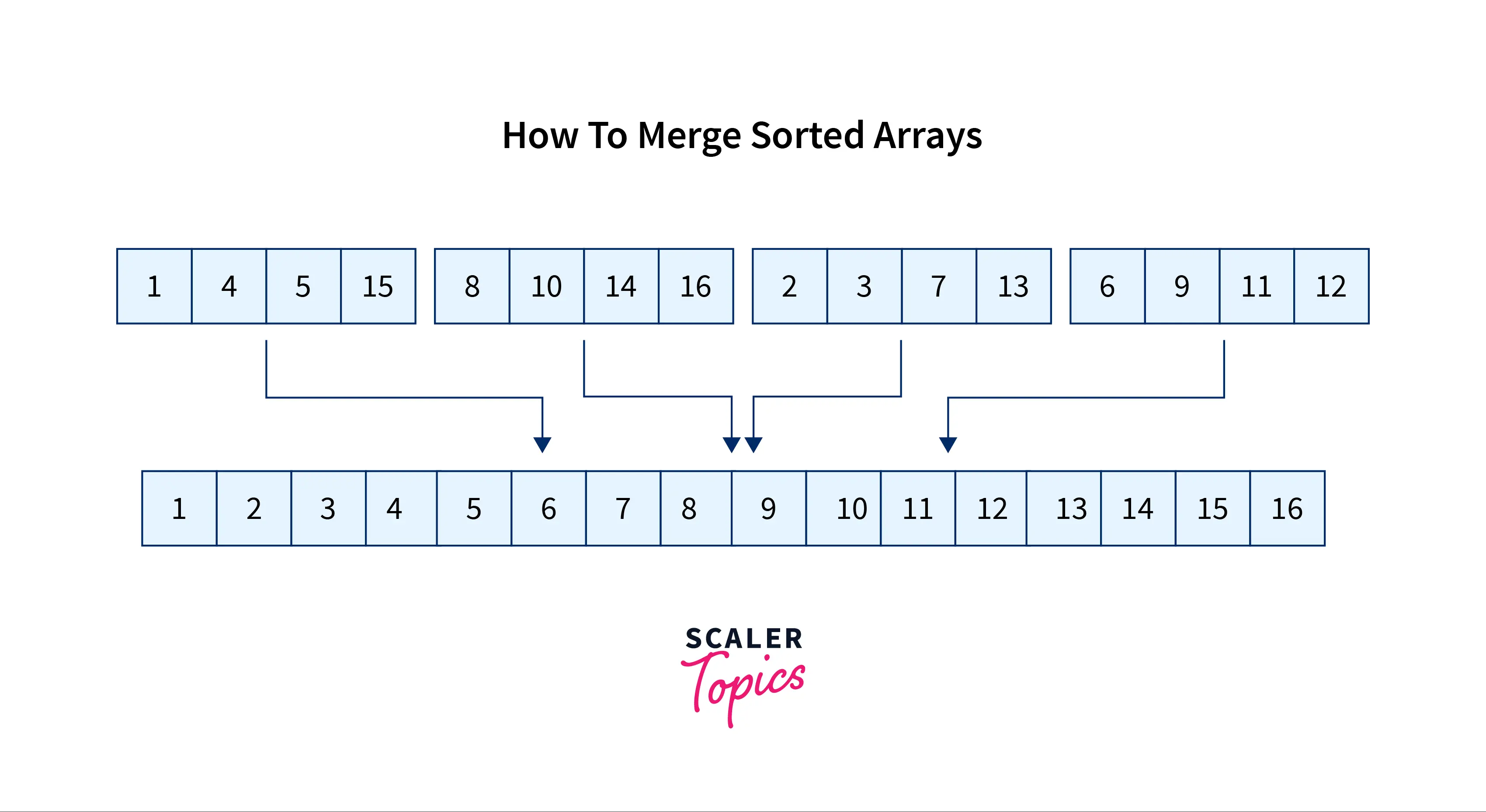
Output:

Explanation

The array at the output is sorted by combining elements of all the three arrays of input.

Constraints

$1 <=n<=10^5$

The Sum of the size of all the arrays will be less than $10^5$

$1<=s[i]<=10^9$

Approach 1 (Naive Approach)

In the naive approach, create an array of size $(k*n)$ and copy elements of the array in another array which is an output array and sort the final output array.

The algorithm of the naive approach is:

1. Create an array for output of size $(k*n)$
2. Traverse the matrix given from start to end and copy or insert all the elements in an output array.
3. Sort the output array and print it.

Code Implementation(in C++, java , python)

C++ program to merge k sorted arrays

Java program to merge k sorted arrays

python program for merging the array

Output

Time Complexity O(k*n*log(k*n)) Because the resulting array is of N*k size.

Space Complexity O(k*n), The output array is of size nk.

Approach 2 (Efficient Approach )

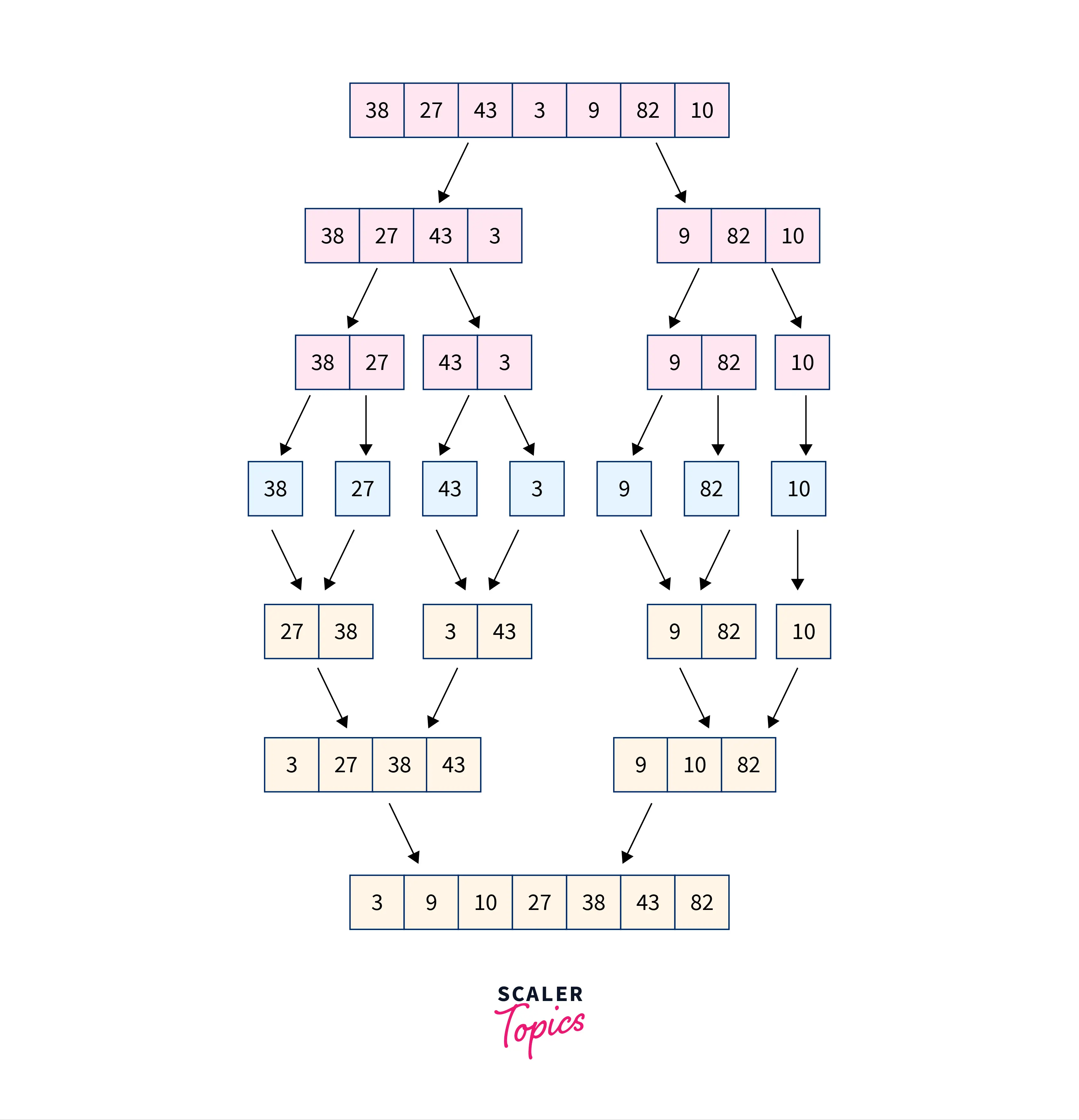
Algorithm

1. Create a function that is recursive, takes the k array, and returns the output array.
2. If the value of k in the recursive function is 1 then return the array else if the value of k is 2 then, merge the array in linear time.
3. If the value of k > 2, then divide the group of k elements in an array in two equal parts and call the function recursively. This means 0 to k/2 in the first recursive function and k/2 to k in the other recursive function.
4. Print the output array

Example:

Code Implementation(in C++, java , python)

C++ program to merge k sorted arrays of size n each

Java program to merge k sorted arrays of size n each.

Python program to merge k sorted arraysof size n each.

Output

Time Complexity

$O( n * k * log k)$ Because there are log(k) levels at each recursive level which are divided into two halves at each k level.

Space Complexity

$O( n * k * log k)$ Each level requires O(n * k) space for storing elements in an array.

Approach 3 (Using min-heap)

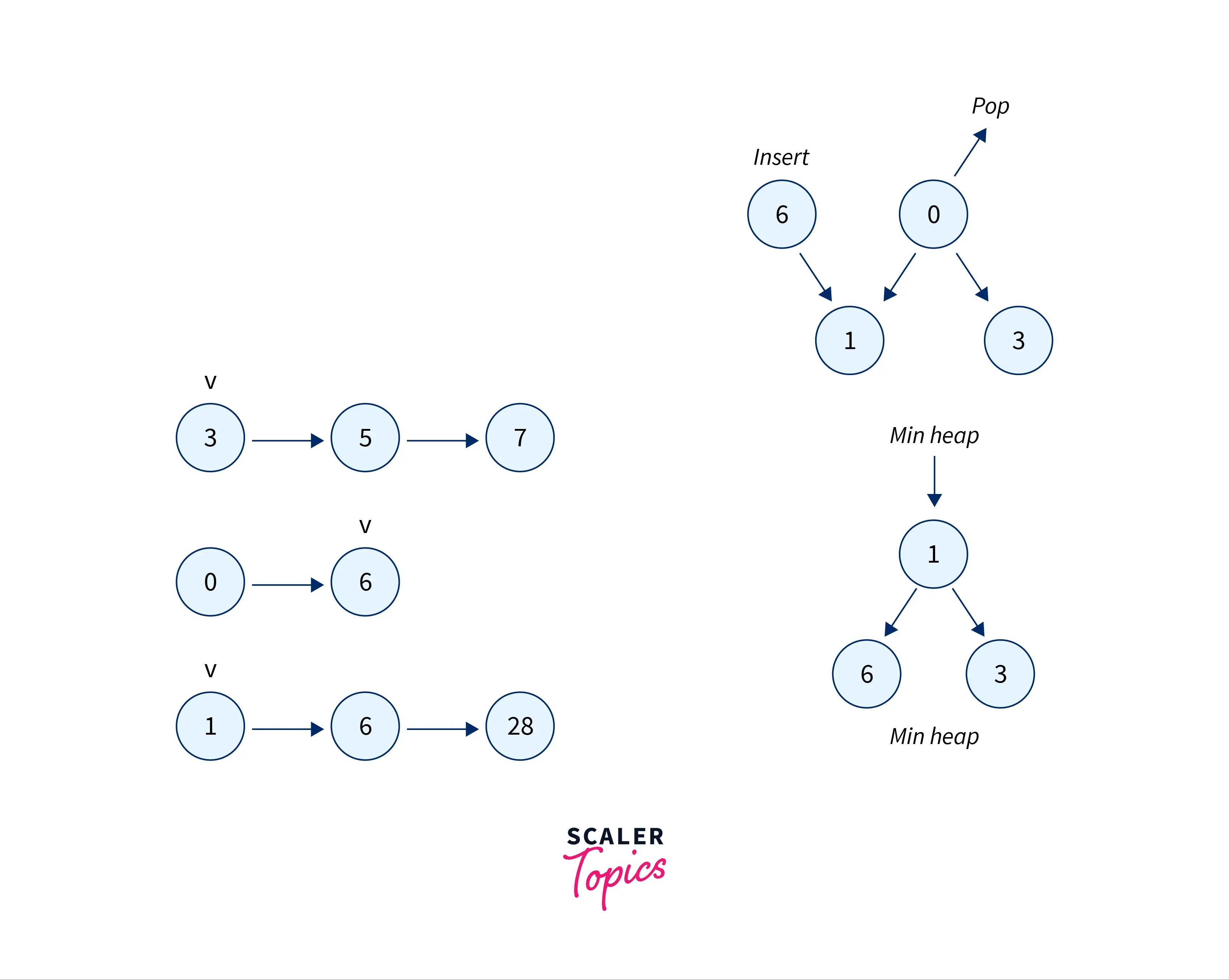
Algorithm

• Create a min-heap and insert into it all the first elements of all the k number of arrays.
• Iterate through the loop until the length becomes 0
• Remove the element from the top of the min-heap and add it to output array
• Insert the next element in the same array until there are no more elements left.

Example:

Code Implementation(in C++, java , python)

Java program to merge k sorted array

Python program to merge k sorted array

Output

Time Complexity

$O( n * k * log k)$ because insertion and deletion of element in min heap requires log k time.

Space Complexity

$O(k)$ space required by min-heap.

Merge k Sorted Arrays | Set 2 (Different Sized Arrays)

Approach

We would use a min-heap that would return the smallest element in constant time O(1) instead of searching through all k elements.

Example:

Input:

Output:

Algorithm

1. Create an array for storing the output
2. Create a min heap of k size and insert the first element of heap in all the array
3. Till the priority queue is not empty,, repeat the below steps:
   • Remove min element from the heap and store it in the output array
   • Insert the next element of array and do it until the array is empty

Code Implementation(in C++, java , python)

C++ program to merge k sorted arrays of n size

Java program to merge k sorted arrays of n size

Python program to merge k sorted arrays of n size

Output

Time Complexity

O(N Log k) because it is heap-based.

Space Complexity

O(N) because of output array.