Merge Sort in C++

Overview
Sorting is arranging elements of an array or a list in increasing or decreasing order. There are many sorting algorithms, like count sort, merge sort, insertion sort, etc., with a certain time and space complexities.
Merge sort in C++ is a divide-and-conquer strategy-based sorting algorithm to arrange a given array or list in optimal time complexity.
Introduction
The merge sort algorithm is an algorithm based on the divide and conquers strategy of solving problems. In this, we divide a problem into several sub-problems, each of which is solved individually, and after that, all of them are combined to give the final solution.
John von Neumann invented it in 1945. We can visualize it as a recursive algorithm that continuously breaks the array into half until the array is left with only 1 element, i.e., this is the base condition to stop the recursion, and then each call returns to its parent and is arranged to return the sorted array finally.
How Merge Sort in C++ Work?
Merge sort works on the divide and conquer principle of solving problems. Here the given problem is divided into multiple subproblems, and we solve and conquer them individually. When the solution for each problem gets ready, we combine all of them to solve the main problem.
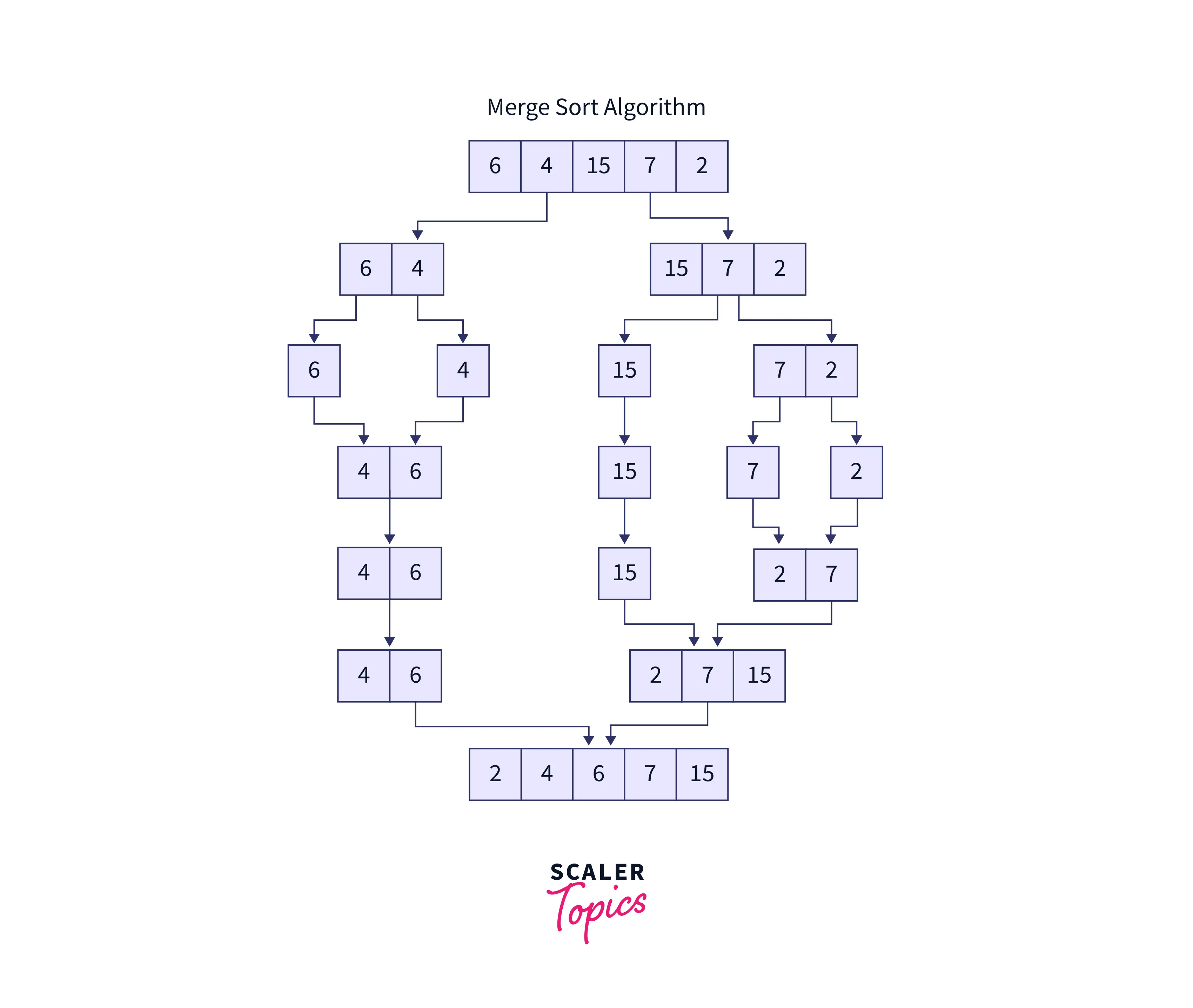
The first stage is where the list is split, forming individual components called sublists. The merging process starts, in which the sublists are paired up again and are arranged in ascending or descending order as per the requirement, and this merging process continues till the sublist form one complete list, and we get our sorted list.
Algorithm
Let's first look at the approach we will follow, and then we will jump right into the code.
- We are given an array arr of size n.
- Check, if n == 0, i.e., we have an empty array, then we have no element to sort.
- If n == 1, ie. there is only one element in the array, then the array is already sorted
- If n > 1, then initialize variables left and right as left = 0 and right = n-1.
- Find middle = (left + right)/2.
- Call mergeSort(arr, left, middle) to recursively sort the first half of the array.
- Similarly, call mergeSort(arr, middle+1, right) to recursively sort the other half of the array.
- Finally call merge(arr, left, middle, right) to merge the obtained sorted arrays.
- Now, the given array is sorted.
C++ Merge Sort Pseudocode
Illustration
Let's understand it through an example.
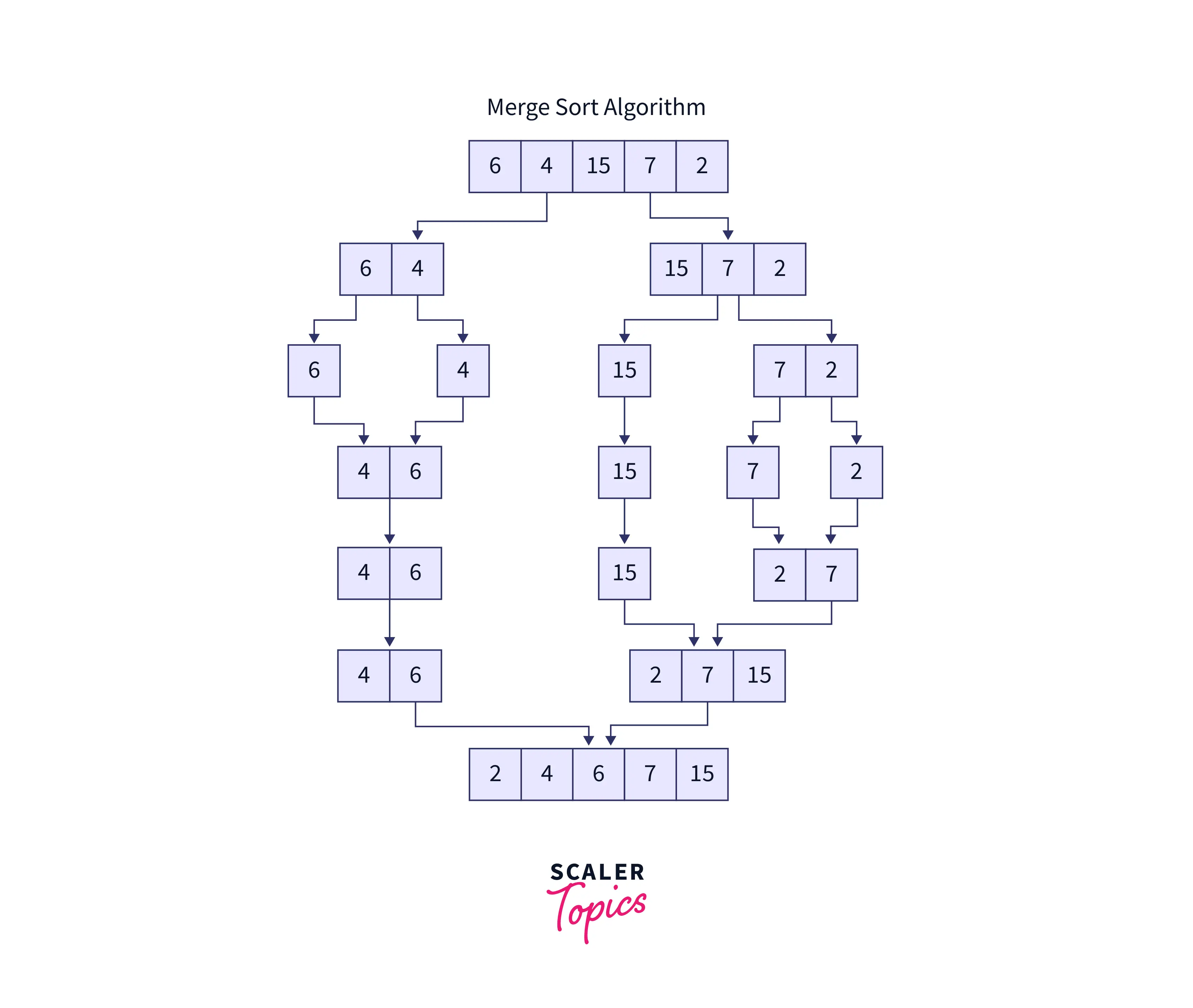
Let's understand the above illustration step by step with the help of a table
| Pass number | Unsorted list | Divide/Merge | Sorted list |
|---|---|---|---|
| 1 | {6,4,15,7,2} | {6,4}, {15,7,2} | {} |
| 2 | {6,4}, {15,7,2} | {6}, {4}, {15}, {7,2} | {} |
| 3 | {6}, {4}, {15}, {7,2} | {4,6}, {15}, {7}, {2} | {4,6} |
| 4 | {4,6}, {15}, {7}, {2} | {4,6}, {15}, {2, 7} | {4,6}, {15}, {2, 7} |
| 5 | {4,6}, {15}, {2, 7} | {4,6}, {2,7,15} | {4,6}, {2,7, 15} |
| 6 | {4,6}, {2,7,15} | {2,4,6,7,15} | {2,4,6,7,15} |
| 7 | {} | {} | {2,4,6,7,15} |
C++ Program to Implement Merge Sort Using 2 Temp Subarrays
In this example, we will be implementing a merge sort algorithm by creating two temporary arrays.
Output
Explanation
- Starting with the main function, we are given an unsorted array. To proceed further, firstly, we have to calculate its length, i.e., the number of elements the array has, after that we are calling the printArray() function to print the array in its current, i.e., unsorted state, and after that, we are calling the mergeSort() function with parameters as the array itself, the starting index from where we want the sorting to begin and the ending index till where we want to continue the sorting.
- Now, let's head to the definition of the function mergeSort(). Here we are declaring a new variable named mid. The reason is, as the whole algorithm of merge sort is to divide a problem into smaller sub-problems and solve them individually, so to perform any division, we would require a midpoint concerning that we will divide the list into two parts. After that, we check a condition -- if the value of starting index, i.e., low, is less than the value of the ending index, i.e., high, then only we are initializing the mid and recursively calling the mergeSort() function with the divided set of lists. The if condition here is the termination condition of this recursive tree, and once that encounters, each call will return to its parent and execute the follow-up function, the merge().
- The merge() function then will combine all the individual solutions and will form them into one complete array. Here in this example, we are merging the individual solutions using two temporary arrays, arrLeft and arrRight, denoting the left and right parts of a list, respectively. After that, we copy the data from the main array and initialize it into both arrays. Then there is a while loop in which we check which one of the left and right temp arrays has a lesser element, and we reinitialize the main array with that element. We continue this until all the elements of at least one array get completely copied to the main array. Then after that, we will exit that loop and copy the remaining elements of the other temp array to the main array as it is so the whole array gets sorted.
C++ Program to Implement Merge Sort Using 1 Temp Subarray
In this example, we will implement the merge sort algorithm using only 1 temporary array.
Output
Explanation
- Here again, starting with the main function, we are given an unsorted array. To proceed further, firstly, we have to calculate its length, i.e., the number of elements the array has. After that, we call the printArray() function to print the array in its current, i.e., unsorted state. After that, we call the mergeSort() function with parameters as the array itself, the starting index from where we want the sorting to begin, and the ending index till where we want to continue the sorting.
- Now, let's head to the definition of the function mergeSort(). Here we are declaring a new variable named mid. The reason is as the whole algorithm of merge sorting is to divide a problem into smaller sub-problems and solve them individually, so to perform any division we would require midpoint concerning that we will divide the list into two parts, after that we are checking a condition if the value of starting index, i.e. low is less than the value of ending index i.e., high then only we are initializing the mid and recursively calling the mergeSort() function with the divided set of lists, the if condition here is the termination condition of this recursive tree, and once that encounters, each call will return to its parent will execute the follow-up function, the merge().
- Here in this, the merge() function will behave slightly differently. Here we are simply creating a temp array and doing the same procedure as we did above, but with a slight variation. Here we are operating on the main array itself. We are setting a midpoint to the main array and two counters, i and j, where i starts from the passed low parameter, and j starts from one ahead of the passed mid parameter, and we are starting to compare elements from those positions, and whichever we get as lesser we are copying it into the temp array, this process will continue till at least one of the counter of i, and j reaches its end, and then we are exiting that loop and copying the remaining elements of the other counter section as it is. And in this way, the temp array is now storing the sorted array, and finally, we are copying the whole temp array again into the main array, which gets sorted.
Iterative Merge Sort in C++
In both the above examples, we have seen the recursive approach of the merge sort algorithm. Now let's look at how we can implement the same algorithm iteratively.
Output
Complexity Analysis of Merge Sort in C++
- As we know, the merge sort algorithm is based on the divide and conquer technique, in which we divide a given array into two smaller and equal sub-arrays. Then we again divide them into two halves and so on until we are left with only 1 element. Hence the number of steps taken in the following operation will be at most .
- Now, finding the middle element will only take a single step, hence .
- After that, while merging the sub-arrays into the original array of size n, the time required will be .
- Hence the total time taken to perform the merge sort operation will be , which is .
In short,
| Case | Complexity |
|---|---|
| Best case time complexity | O(nlogn) |
| Average case time complexity | O(nlogn) |
| Worst case time complexity | O(nlogn) |
| Space Complexity | O(n) |
We can see that the time complexity for merge sort is the same in all three cases (best, average, worst), as in all of the above cases, it divides the given array into subarrays. Then it merges them into the main array, making it take the same amount of time, irrespective of the case.
Applications of Merge Sort in C++
- One of the most useful applications of the merge sort algorithm is to sort linked lists in time complexity, as in linked lists, the nodes need not be adjacent to each other in the memory, unlike the arrays. Hence, we can insert new elements in the middle of linked lists in time and space complexity. All we have to do is shift the respective nodes' pointer linkings, which in turn means the merge process for the merge sort algorithm can be implemented without taking up any extra spaces in linked lists.
- Merge sort can also be used to count inversions in a list.
- We can also use the merge sort for external sorting.
Advantages and Disadvantages of Merge Sort in C++
Advantages
- Merge sort can efficiently sort a given list or array in time.
- Merge sort can easily be used to sort linked lists without taking up any extra memory space.
- It can count the number of inversions in the list.
Disadvantages
- For smaller problems or data sets, merge sort is slower than other sorting algorithms.
- For the temporary array we create, merge sort takes an additional space of .
- If the given array is already sorted, then merge sort goes through it at least once.
Conclusion
- Merge sort is a sorting algorithm based on the divide and conquers strategy to sort elements of an array which is comparatively faster as compared to other sorting techniques
- In this, we first split the given array into half, then break those halves again into half, and this process continues till the array is left with single elements. Then we arrange and pair them all up again to form the main sorted array.
- The best, average, and worst case complexity of merge sort are the same in all three cases .
- Merge sort works well for large data sets or large arrays, as it almost takes linear time to sort them, but for smaller datasets, merge sort behaves comparatively slowly compared to its other counterpart algorithms.
