Merge Sort in Python

Introduction

In merge sort, the given array is divided into roughly two equal sub-arrays. These sub-arrays are divided over and over again into halves until we end up with arrays having only one element each. At last, we merge the sorted pairs of sub-arrays into a final sorted array.

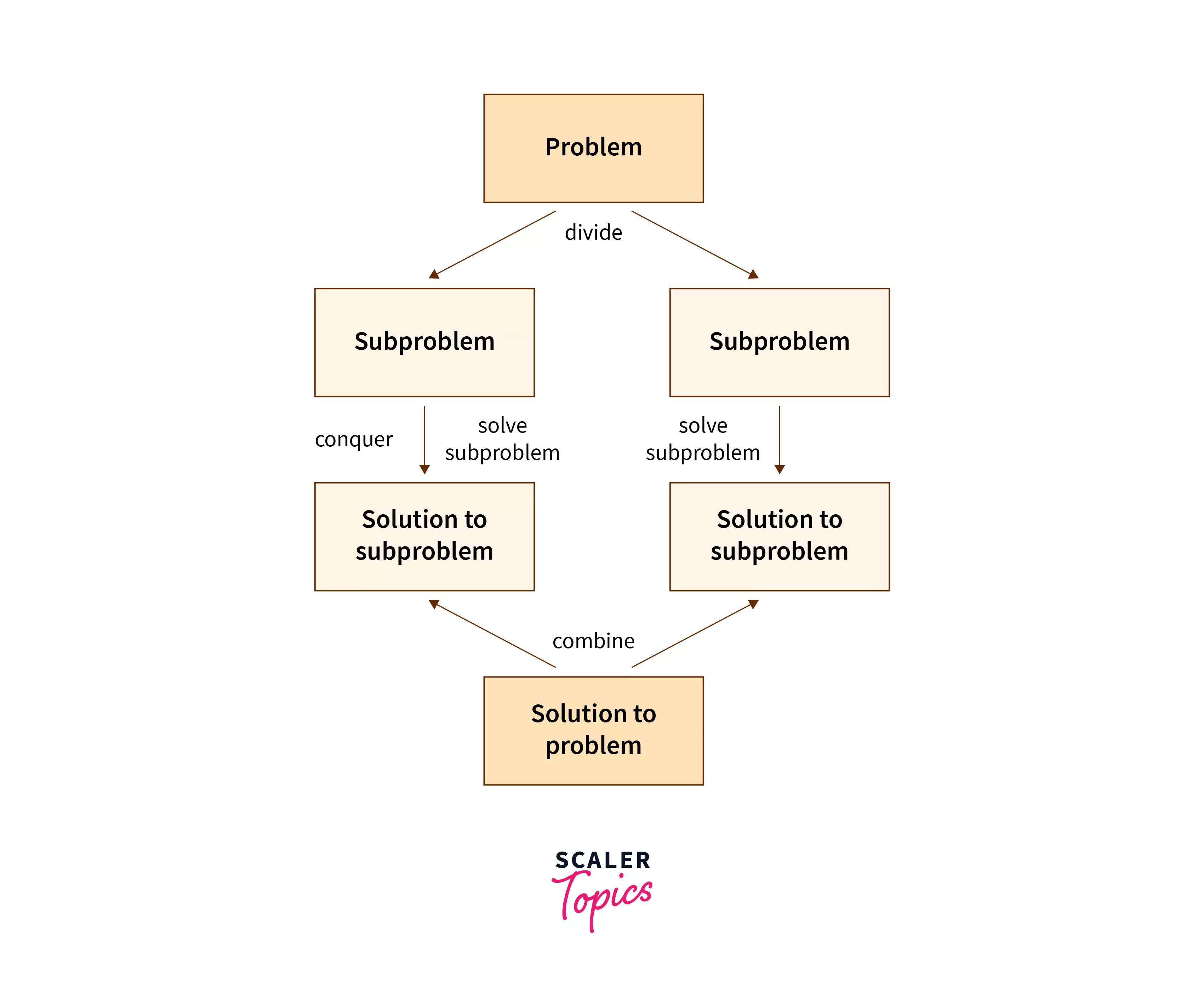
How does Divide and Conquer work?

Let us now learn how divide and conquer technique is applied to sort an array of integers. Consider an array, that consists of n number of unsorted integers. Our result should be a sorted array.

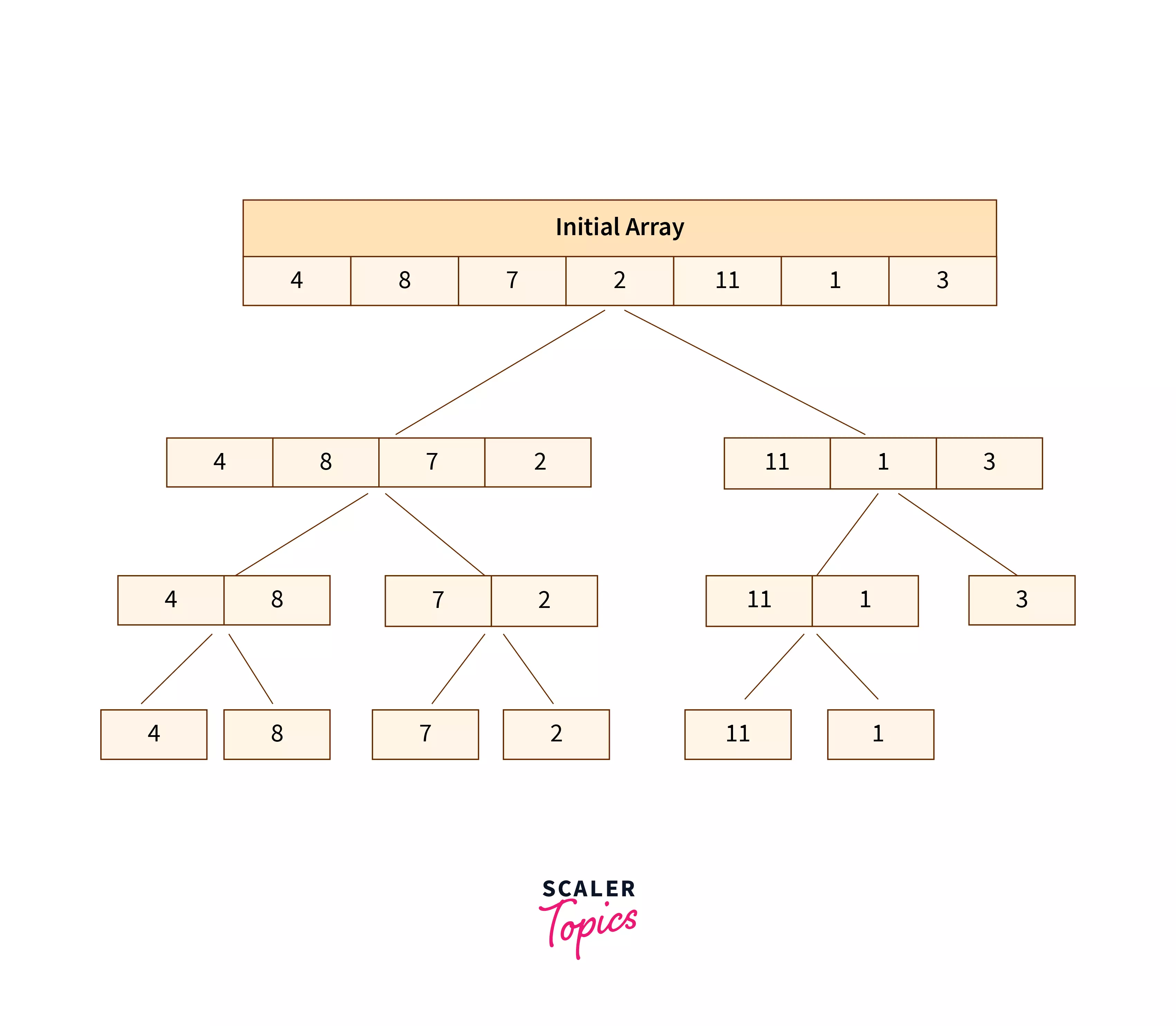
Let us consider an array = [4, 8, 7, 2, 11, 1, 3].

• 1. Divide For dividing the array, we calculate the midpoint of the array by using the formula mid = len(array)//2

• 2. Conquer In this step, we divide the array into sub-arrays with the help of the midpoint calculated. This division into sub-arrays and calculation of midpoint is done recursively for the same. As we know, a single element in an array is always sorted. Therefore, we have to continuously divide the sub-arrays until all elements in the array are single array elements.

Once this step is completed, the array elements are merged back to form a final sorted array.

• 3. Combine Since, now we are done with the formation of sub-arrays, the last step is to combine them back in sorted order.

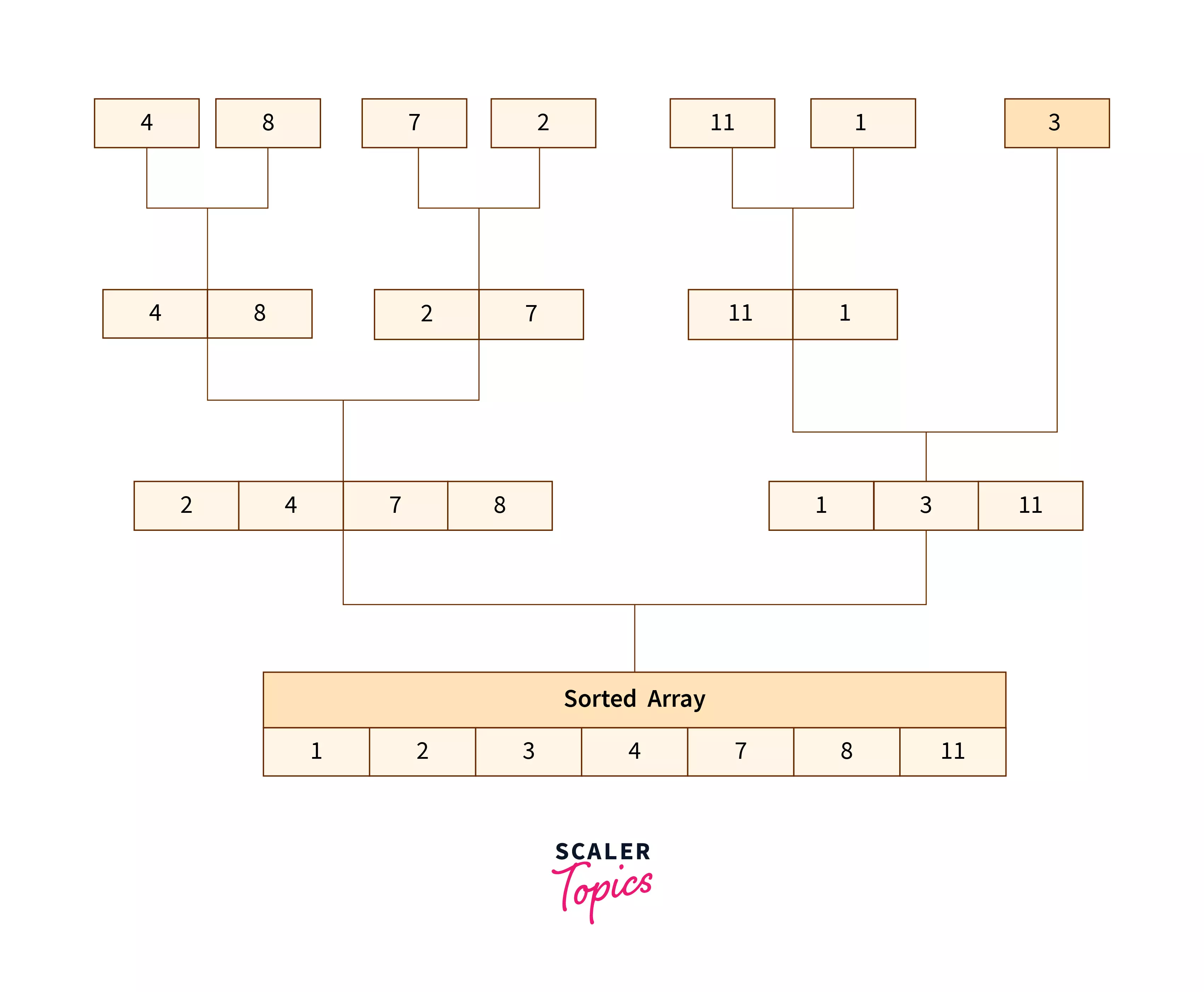
For a detailed explanation of how merge sort works check this article

Python Programs for Merge Sort

In this section, we will implement a merge sort algorithm in python on two types of collections - integer element's array and custom objects.

• Sorting Array The merge sort algorithm divides the given array into roughly two equal halves and sorts them recursively. This process is continued until arrays have only one element left.

  1. The First step is to create copies of arrays. The first array contains the elements from [start_index,middle] and the second from [middle+1,end_index].
  2. In second step, we traverse both copies of the array with the help of pointers and select the smaller value of the two values and add them to the sorted array.
  3. The Last step is, if we run out of elements in any array, we select the remaining elements and place them in the sorted array.

Let us now implement merge sort algorithm in Python.

Output

By calling the merge method last, we make sure that all the divisions will happen before we start the sorting. We use the // operator to be explicit about the fact that we want integer values for our indices.

• Sorting Custom Objects Since now we are familiar with the basics of merge sort in python, let us use the same as above for sorting our custom objects, which in most cases isn't what we want. A better idea is to make the algorithm itself more versatile, and pass a comparison function to it.

First, we'll implement a custom class Product and add a few fields to it:

Output

In the above program, We've implemented Merge Sort both on custom class objects with the help of a lambda function used for comparison.

Time complexity of merge sort in python

Time Complexity Merge Sort’s time complexity is $O(nLog n)$ in the worst case, the average case, and the best case because it always divides the array into two halves and merges the two halves in linear time.

Space Complexity We require an additional array sorted to store the resultant sorted array, hence the space-time complexity is $O(n)$.

Learn from industry experts and get certified in Python programming. Enroll in our Python Course today and boost your professional credibility.

Optimization

There are two main methods using which we can implement the Merge Sort algorithm, one is using a top-down approach (recursive) like in the example explained above, which is how Merge Sort is most often implemented. The top-down approach is multi-threading.

The other approach is bottom-up approach, which works similar to the second half of the top-down approach where instead of recursively calling the sort on halved sub-arrays, we iteratively sort adjacent sub-arrays. This means is that, given an array such as [4, 8, 7, 2, 11, 1, 3], instead of breaking it down into [4], [8], [7], [2], [11], [1] ,[3] - it's divided into subarrays which may already be sorted: [4,8], [7}, [2,11], [1,3] and then sorting them.

Merge Sort is however relatively inefficient (both time and space) when it comes to smaller arrays, and is often optimized by calling Insertion Sort on smaller sub-arrays to sort them, before merging into a larger array. This is because Insertion Sort works really well with small and/or nearly sorted arrays.

Read More:

• selection sort in Python.
• Sort a String in Python.
• Sort Dictionary by Key in Python.
• Sort Dictionary by Value in Python.
• Sorted Function in Python.