Java Program for Merge Sort
FREE
Merge Sort program in Java is one of the most respected sorting algorithms, with a worst-case time complexity of O(nlogn). It works on the divide and conquer algorithm. It operates on the recursive division of the problem into subproblems, which are then combined to produce the final output (Sorted elements). The algorithm is based on the recursion approach but can also be implemented iteratively.
Transform Your Career
Choose from our industry-leading programs designed for career success
Modern Software and AI Engineering Program
Master full-stack development with AI integration
+1000 moreModern Data Science and ML with specialisation in AI
Advanced data science techniques with AI specialization
+1000 moreAdvanced AIML with Specialisation in Agentic AI
Deep dive into AIML with focus on Agentic systems
+1000 moreDevOps, Cloud & AI Platform Engineering
Build and manage AI-powered cloud infrastructure
+1000 moreAI Engineering Advanced Certification by IIT-Roorkee
Premier AI engineering certification from IIT-Roorkee
Merge Sort Algorithm
Merge Sort is a well-known and successful sorting approach that uses the divide and conquer algorithm to divide a problem into many sub-problems. Let's see its algorithm and how it works:
- The array is recursively split into halves until each contains only one element.
- A merge() function combines two sorted sub-arrays into one.
- The process continues until the list is indivisible (each part has one element).
- The merging step starts with combining one-element lists, then progresses to two-element lists, and so forth, until the entire array is sorted.
Java Program for Merge Sort
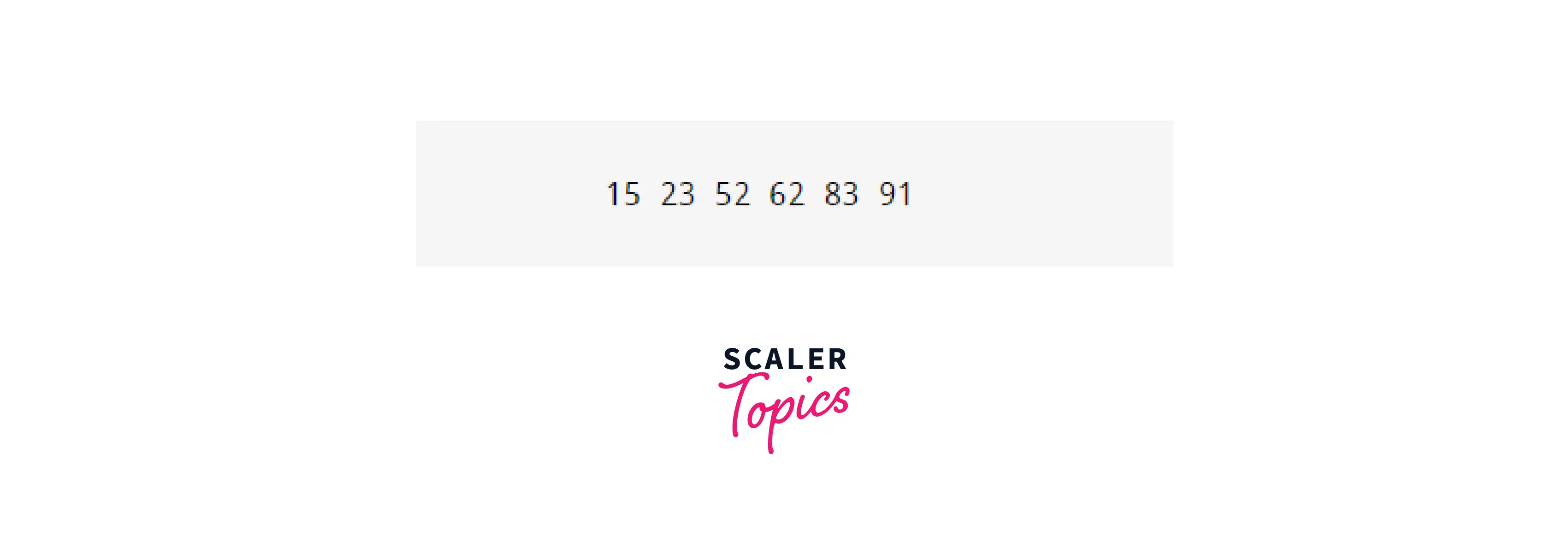
Output:
Complexity Analysis
- Time Complexity: O(nlogn)
- Auxiliary Space: O(n)
In the example, we start with an unsorted array. Using the merge sort program in Java, we recursively break it down into smaller parts until each part is sorted individually. Then, we merge these sorted parts in ascending order to get the final sorted array. To learn more about merge sort complexity analysis, visit Merge Sort Algorithm.
Advantages of Merge Sort
- Merge sort maintains the relative order of equal elements, ensuring stability.
- Its worst-case time complexity of O(NlogN) guarantees efficient performance, even with large datasets.
- The algorithm is naturally parallelizable, seamlessly utilising multiple processors or threads.
Conclusion
- Merge sort program in Java is a divide-and-conquer algorithm that calls itself recursively on halved pieces of the original collection.
- Merge Sort is an "out-of-place" sorting method. This means it needs more capacity to store the components it's sorting.
- Despite being one of the fastest and most efficient sorting algorithms, with an average time complexity of O(nlogn), it ranks with Quicksort, Timsort, and Heapsort.
Google
Amazon
Microsoft
Flipkart
Adobe1200+ more