Momentum-Based Gradient Descent

Introduction

Momentum-based gradient descent is a gradient descent optimization algorithm variant that adds a momentum term to the update rule. The momentum term is computed as a moving average of the past gradients, and the weight of the past gradients is controlled by a hyperparameter called Beta. The momentum term helps to accelerate the optimization process by allowing the updates to build up in the direction of the steepest descent. This can help to address some of the problems with vanilla gradient descent, such as oscillations, slow convergence, and getting stuck in local minima. By using momentum-based gradient descent, it is possible to train machine learning models more efficiently and achieve better performance.

Gradient Descent

Gradient descent is an optimization algorithm used to minimize a loss function by iteratively moving in the direction of the steepest descent as defined by the negative of the gradient. We can use it in various settings, such as linear regression and neural networks.

Problems with Gradient Descent

There are a few problems that can occur when using gradient descent:

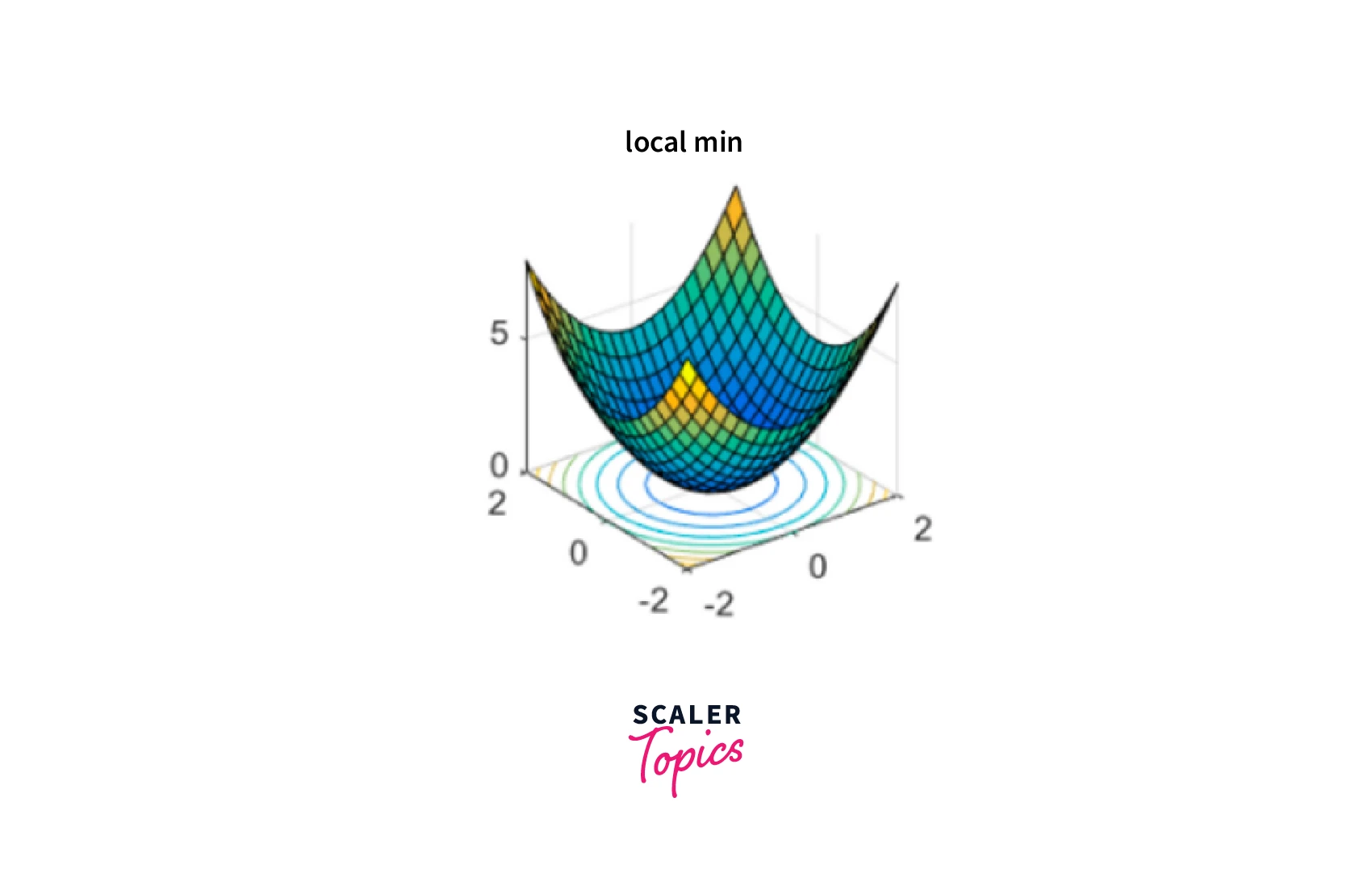
Local Minima:

Gradient descent can get stuck in local minima, points that are not the global minimum of the cost function but are still lower than the surrounding points. This can occur when the cost function has multiple valleys, and the algorithm gets stuck in one instead of reaching the global minimum.

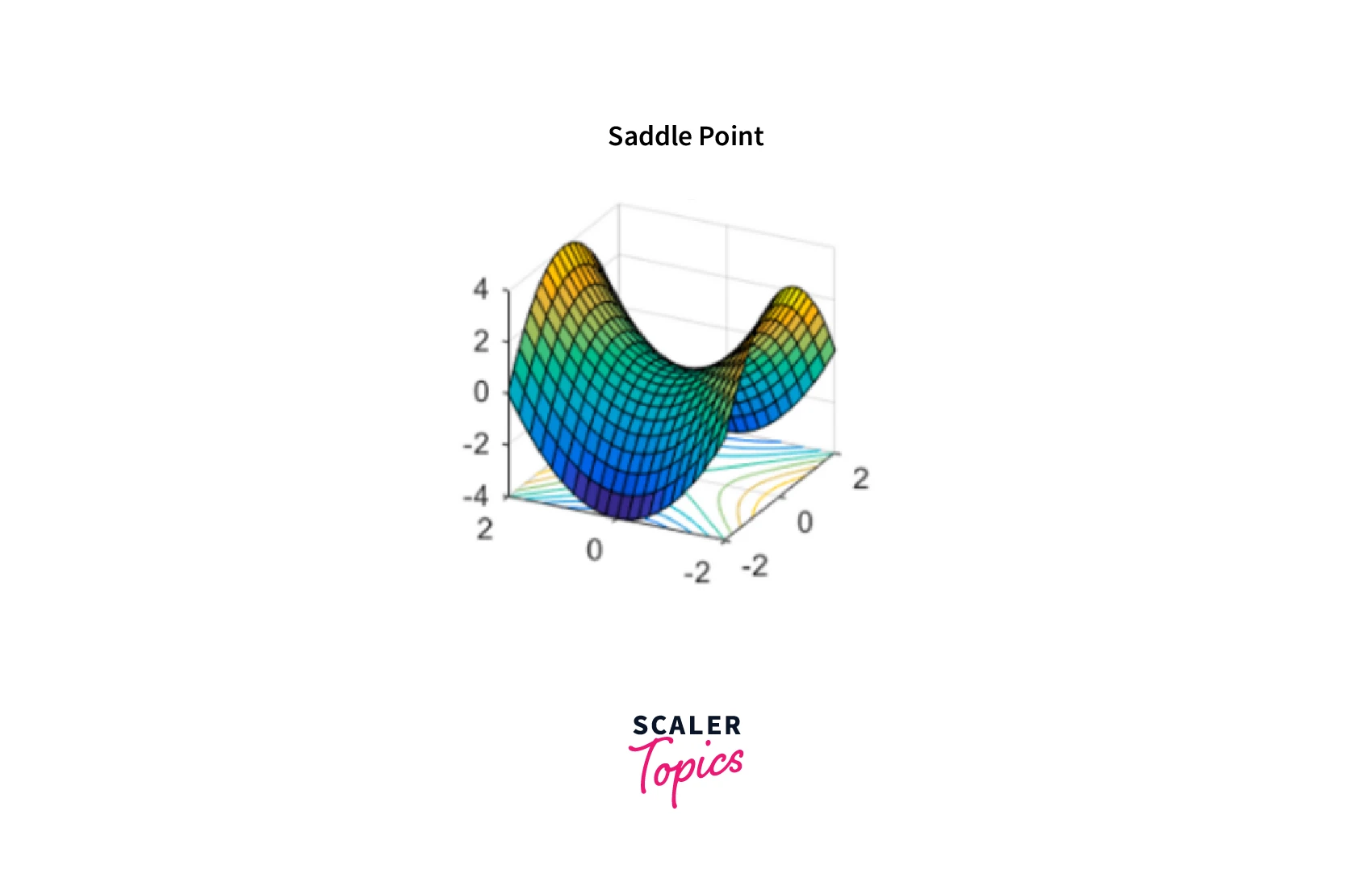
Saddle Points:

A saddle point is a point in the cost function where one dimension has a higher value than the surrounding points, and the other has a lower value. Gradient descent can get stuck at these points because the gradients in one direction point towards a lower value, while those in the other direction point towards a higher value.

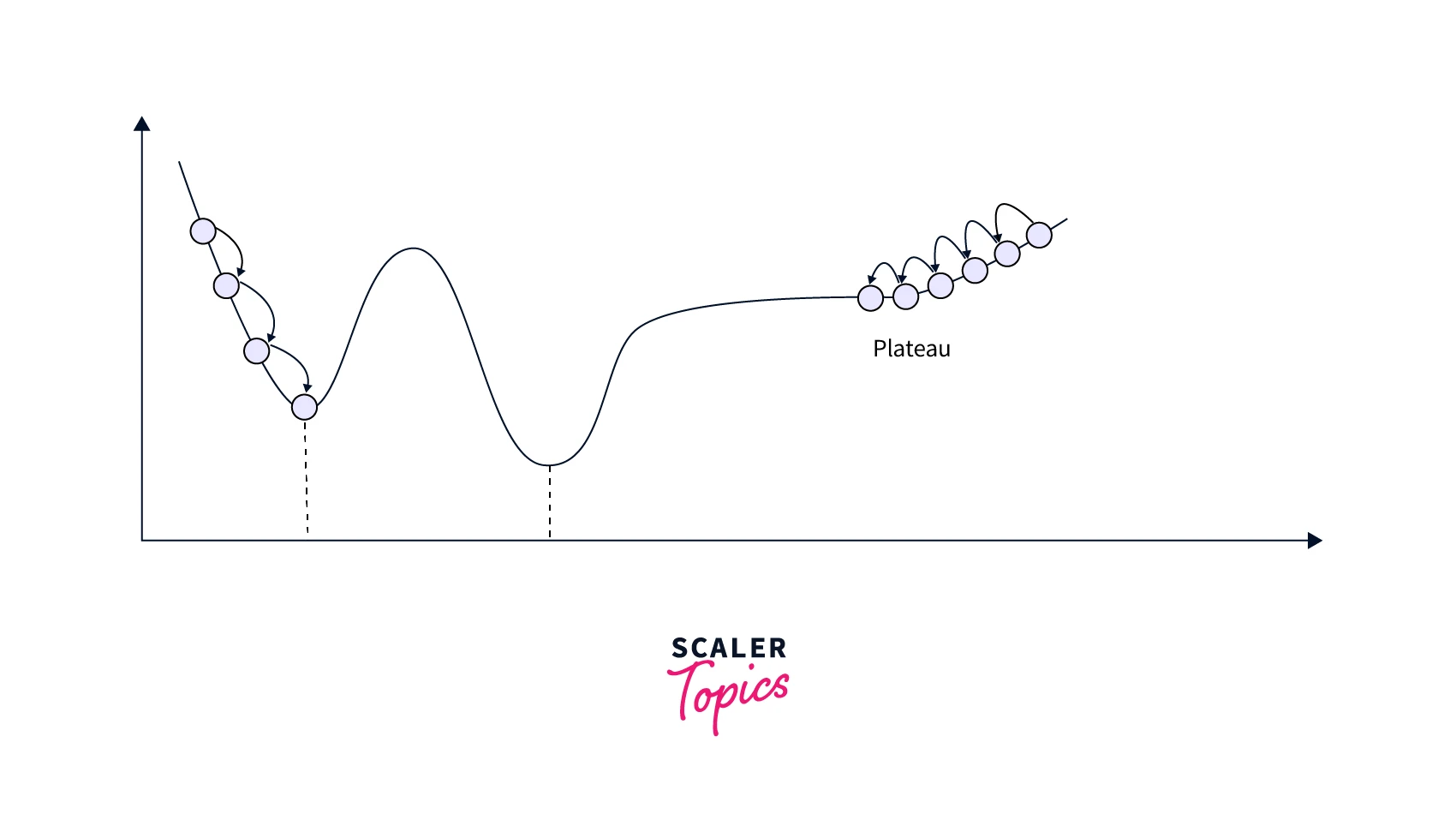
Plateaus:

A plateau is a region in the cost function where the gradients are very small or close to zero. This can cause gradient descent to take a long time or not converge.

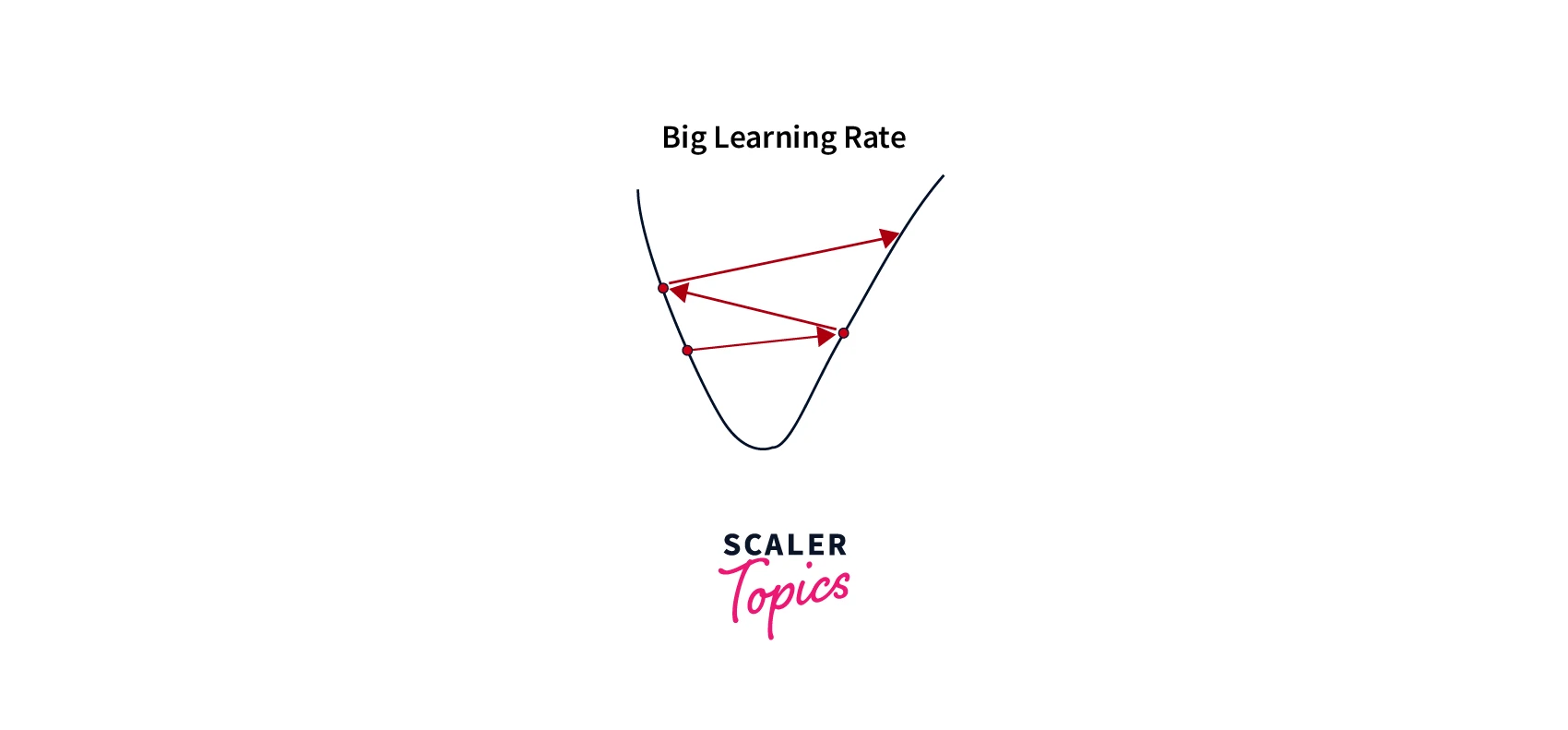
Oscillations:

Oscillations occur when the learning rate is too high, causing the algorithm to overshoot the minimum and oscillate back and forth.

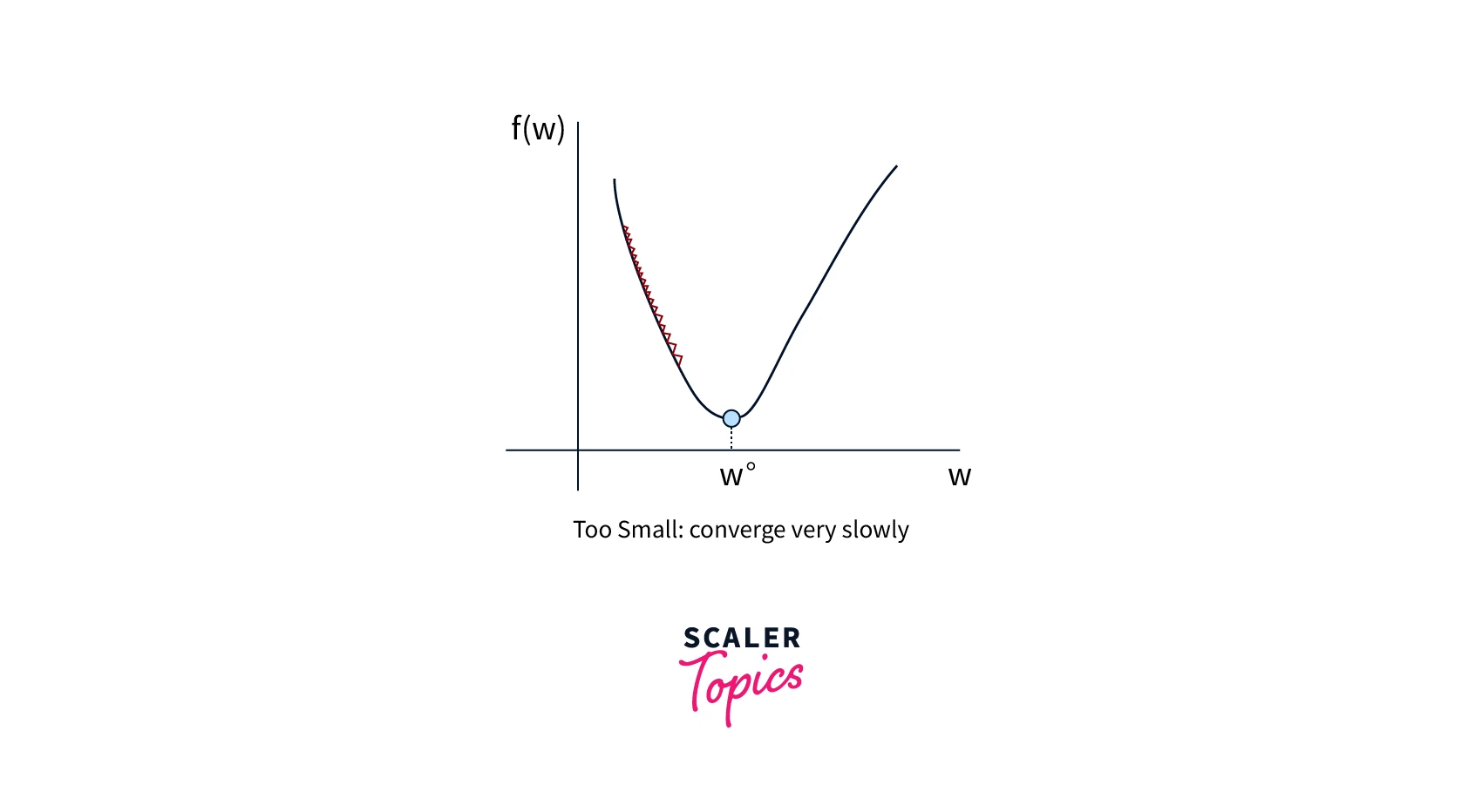
Slow convergence:

Gradient descent can converge very slowly when the cost function is complex or has many local minima. This means the algorithm may take a long time to find the global minimum.

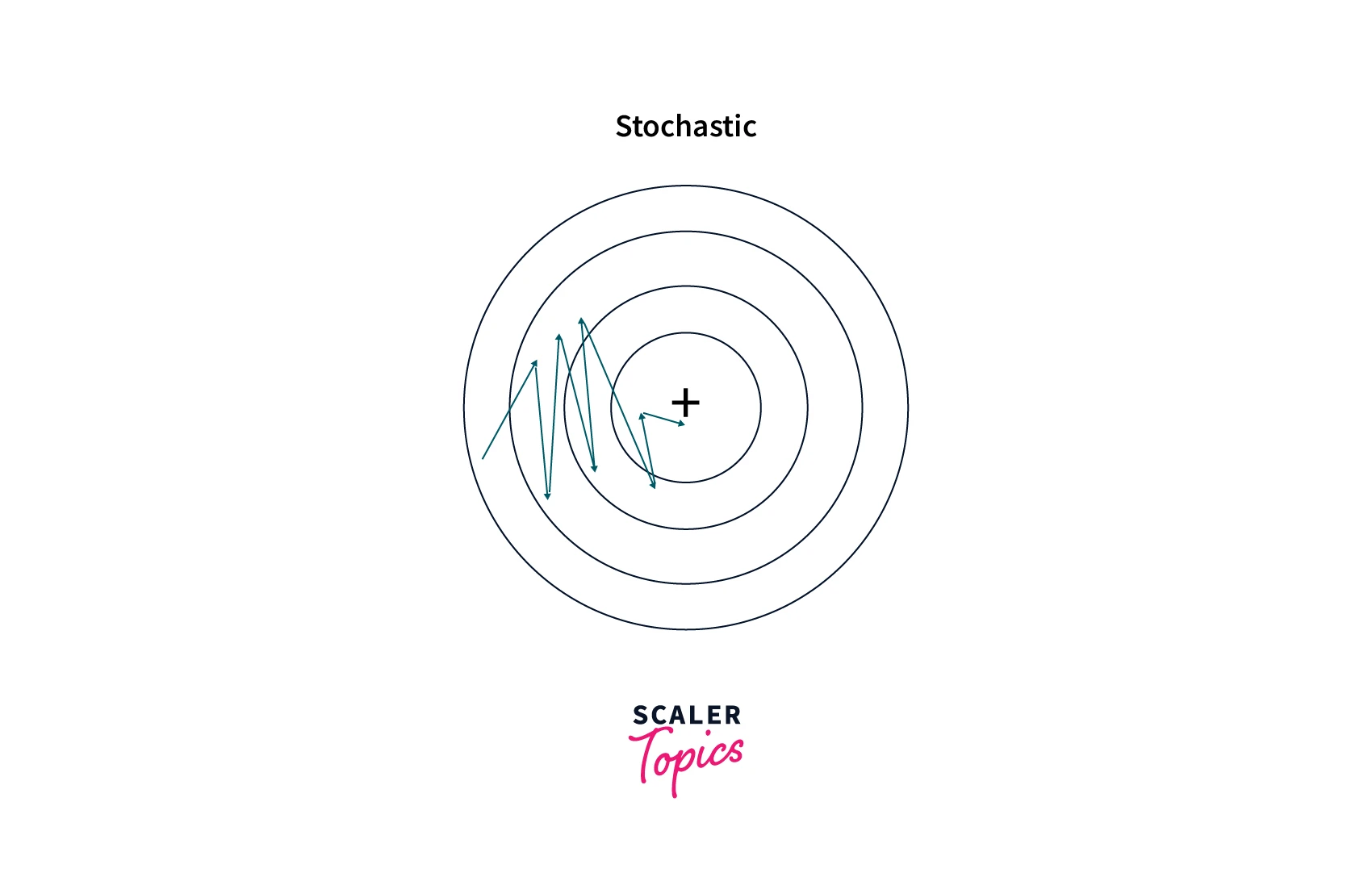
Stochasticity:

In stochastic gradient descent, the cost function is evaluated at random samples from the data set. This introduces randomness into the algorithm, making converging to a global minimum more difficult.

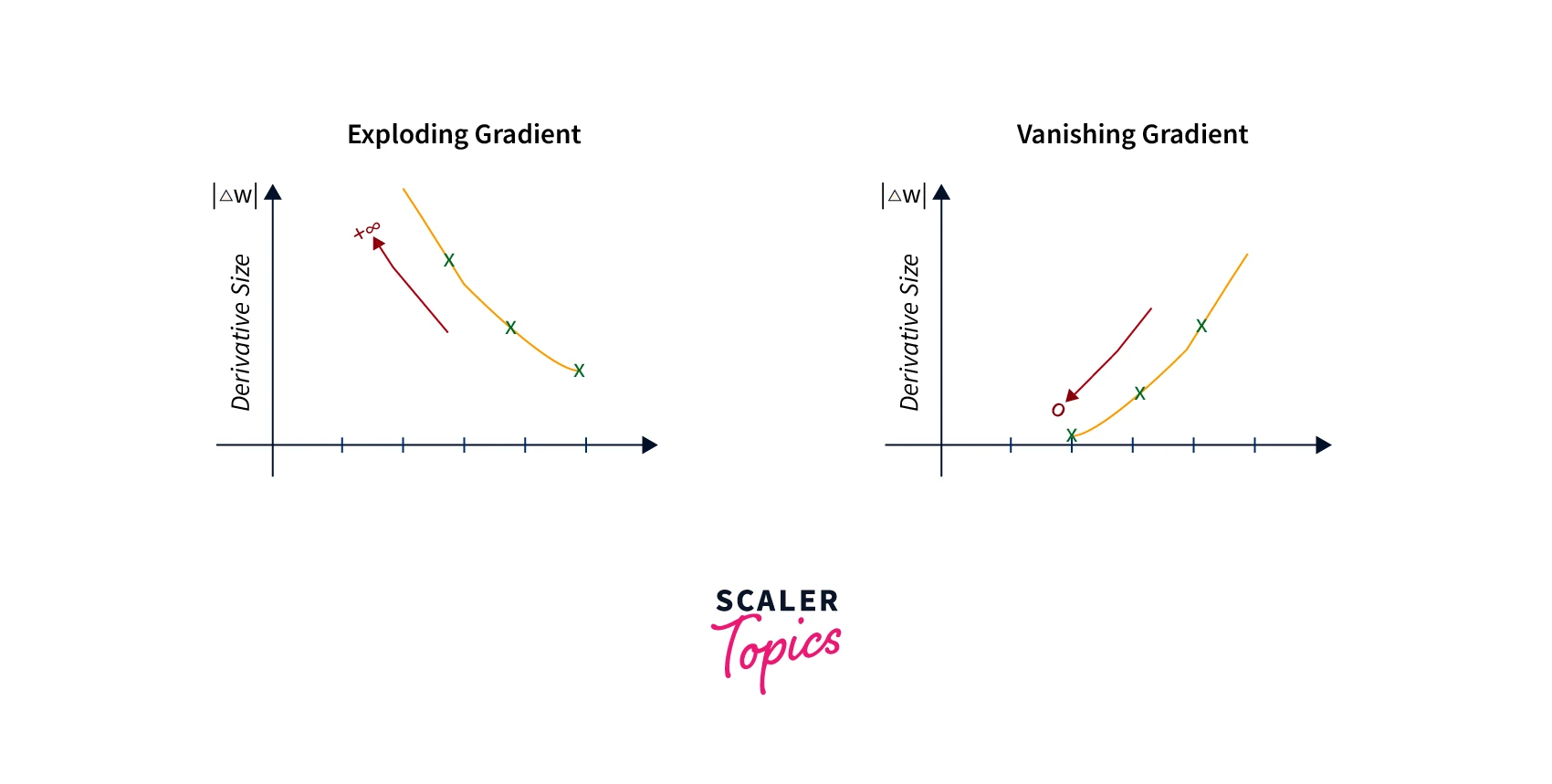
Vanishing or Exploding Gradients:

Deep neural networks with many layers can suffer from vanishing or exploding gradients. This occurs when the gradients become very small or large, respectively, as they are backpropagated through the layers. This can make it difficult for the algorithm to update the weights and biases.

How can Momentum Fix the Problems?

We can use gradient descent with momentum to address some of these problems. It works by adding a fraction of the previous weight update to the current weight update so that the optimization algorithm can build momentum as it descends the loss function. This can help the algorithm escape from local minima and saddle points and can also help the algorithm converge faster by avoiding oscillations.

Momentum helps to,

• Escape local minima and saddle points
• Aids in faster convergence by reducing oscillations
• Smooths out weight updates for stability
• Reduces model complexity and prevents overfitting
• Can be used in combination with other optimization algorithms for improved performance.

How can this be Used and Applied to Gradient Descent?

To apply gradient descent with momentum, you can update the weights as follows:

Where v is the momentum term, rho is the momentum hyperparameter (typically set to 0.9), learning_rate is the learning rate, and the gradient is the gradient of the loss function to the weights.

It's important to note that momentum is just one of many techniques we can use to improve the convergence of gradient descent. Other techniques include Nesterov momentum, adaptive learning rates, and mini-batch gradient descent.

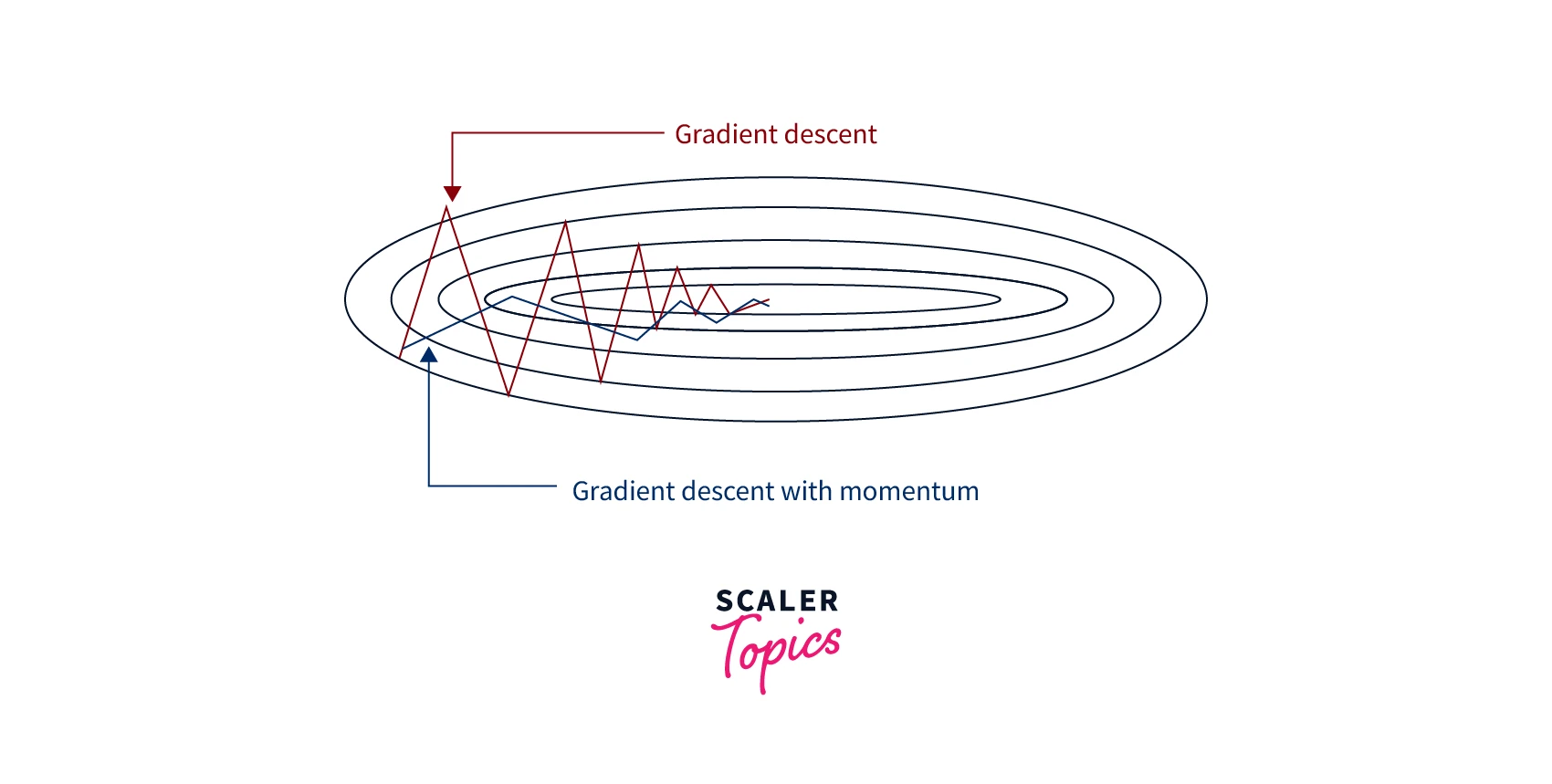
How does Momentum-Based Gradient Descent Work?

Gradient descent with momentum is an optimization algorithm that helps accelerate the convergence of gradient descent by adding a momentum term to the weight update. The momentum term is based on the previous weight update and helps the algorithm build momentum as it descends the loss function.

Here is the math behind momentum-based gradient descent:

Let's say we have a set of weights w and a loss function L, and we want to use gradient descent to find the weights that minimize the loss function. The standard gradient descent update rule is:

Where alpha is the learning rate, and the gradient is the gradient of the loss function to the weights.

To incorporate gradient descent with momentum into this update rule, we can add a momentum term v that is based on the previous weight update:

Where rho is the momentum hyperparameter (typically set to 0.9).

The momentum term v can be interpreted as the "velocity" of the optimization algorithm, and it helps the algorithm build momentum as it descends the loss function. This can help the algorithm escape from local minima and saddle points and can also help the algorithm converge faster by avoiding oscillations.

Implementation of Momentum-based Gradient Descent

Define the Data Points

The code defines the data points x and y as input and target values lists.

Gradient Calculation Function

The dJ function calculates the gradients of the cost function to the parameters m and b. It takes in the input and target values, as well as the current values for m and b, and returns the gradients of the cost function to these parameters.

Gradient Descent Function

The gradient_descent function performs the optimization process using gradient descent. It takes in the input and target values and optional arguments for the learning rate and the number of iterations. It initializes the parameters m and b to 0, then performs the gradient descent by repeatedly updating the parameters using the gradients calculated by the dJ function.

When the optimization process is complete, the function returns the optimal m and b.

Momentum-based Gradient Descent Function

The momentum_gradient_descent function optimizes using momentum-based gradient descent. It initializes the parameters m and b to 0 and the velocity variables v_m and v_b to 0. It takes in the input and target values and optional arguments for the learning rate, number of iterations, and momentum parameter (gamma).

The function then performs the gradient descent by repeatedly updating the velocity and the parameters using the gradients calculated by the ``dJ` function. The velocity is updated using an exponentially weighted moving average of the gradients, and the parameters are updated using the velocity.

Optimization

The code performs the optimization using both gradient descent and momentum-based gradient descent. It calls the gradient_descent and momentum_gradient_descent functions which return the optimal values for the parameters m and b.

Plotting

The code plots the optimization process for both algorithms using the plot_optimization function. It passes the data points, optimal values for m and b, and a title for the plot.

Ouput:

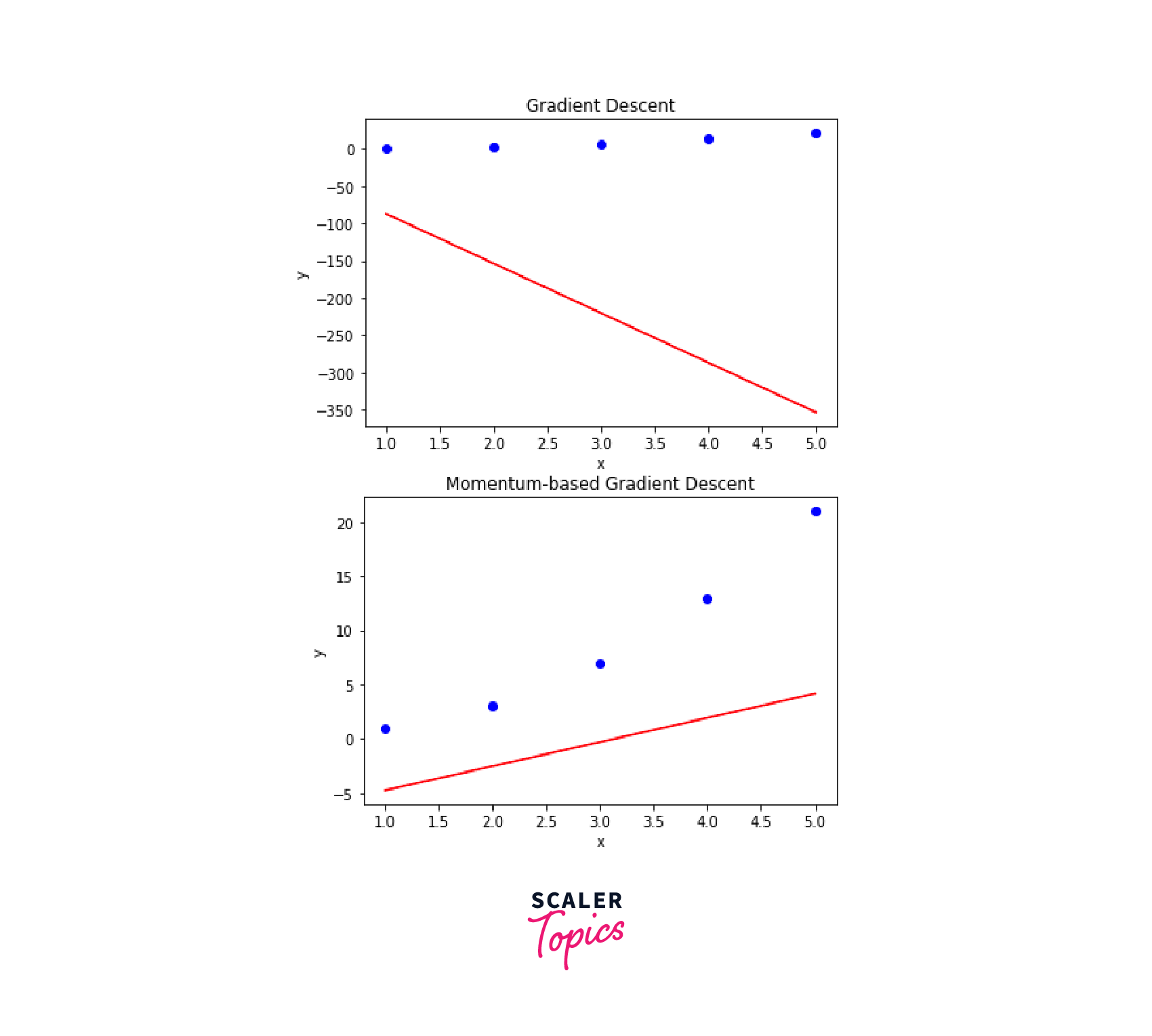
The main difference between the plots for gradient descent and momentum-based gradient descent is the shape of the regression line. In general, the regression line for momentum-based gradient descent will be smoother and less jagged than the line for gradient descent. This is because momentum-based gradient descent uses an exponentially weighted moving average of the gradients to update the parameters, which can help to reduce oscillations and improve the convergence rate.

How to Choose Beta?

In the context of gradient descent, the term "beta" usually refers to the gradient descent with momentum parameter (also known as "gamma") that is used to update the velocity in momentum-based gradient descent. The momentum parameter determines the influence of the previous gradients on the current update of the parameters.

Choosing a good value for the momentum parameter can improve the convergence rate and stability of the optimization process. Generally, a value of 0.9 or 0.99 is often used as a starting point, and We can fine-tune the value based on the specific characteristics of the optimization problem.

Here are a few tips for choosing the momentum parameter:

1. If the momentum parameter is too small (e.g., closer to 0), the optimization process may be slower and oscillate more.
2. If the momentum parameter is too large (e.g., closer to 1), the optimization process may overshoot the optimal solution and not converge.
3. It can be helpful to try a range88 of values for the momentum parameter and see how the optimization process behaves. A good value may depend on the learning rate and the specific characteristics of the optimization problem.