Multiclass Classification in Machine Learning
Multiclass Classification in Machine Learning is a predictive modeling task that involves classifying instances into one of three or more classes. Unlike binary classification, which differentiates between two categories, multiclass classification deals with a broader range of categories, making it crucial for complex decision-making processes in various applications like image recognition, medical diagnosis, and natural language processing.
Classifiers Used in Multiclass Classification
In Multiclass Classification in Machine Learning, several algorithms are adept at handling multiple classes, each offering unique approaches and principles. These classifiers can efficiently navigate through the complexity of multiclass data, making informed decisions on which category a new observation falls into.
Naive Bayes
Naive Bayes classifiers are a family of simple probabilistic classifiers based on applying Bayes' theorem with the strong (naive) assumption of conditional independence between every pair of features given the class variable. Despite their simplicity, Naive Bayes classifiers can achieve high accuracy and speed when applied to large datasets.
Working
The working of Naive Bayes in Multiclass Classification can be outlined in the following steps:
- Model Preparation: It starts with preparing the model by calculating the prior probability of each class in the dataset, which is the frequency of each class divided by the total number of instances.
- Likelihood Calculation: For each feature, the likelihood of the feature given each class is calculated. This involves computing the conditional probability of each feature value given each class.
- Apply Bayes' Theorem: Bayes' theorem is applied to calculate the posterior probability of each class given an observation. The posterior probability is the probability of the class given the observed features.
- Class Prediction: The class with the highest posterior probability is predicted as the output for the given observation.
Formula:
The theorem is articulated through the formula:
Here:
- is the posterior probability of the class given the features, representing the probability that a given instance belongs to a certain class after observing the feature values.
- is the likelihood, which is the probability of the features being observed given that the instance belongs to a certain class.
- is the prior probability of the class, indicating how frequent the class is in the dataset.
- is the prior probability of the features, representing how common the observed feature values are in the dataset.
KNN
K-Nearest Neighbors (KNN) is a non-parametric, instance-based learning algorithm where the function is only approximated locally and all computation is deferred until function evaluation. It's one of the simplest of all machine learning algorithms, with the classification of a sample based on the majority class among its K nearest neighbors.
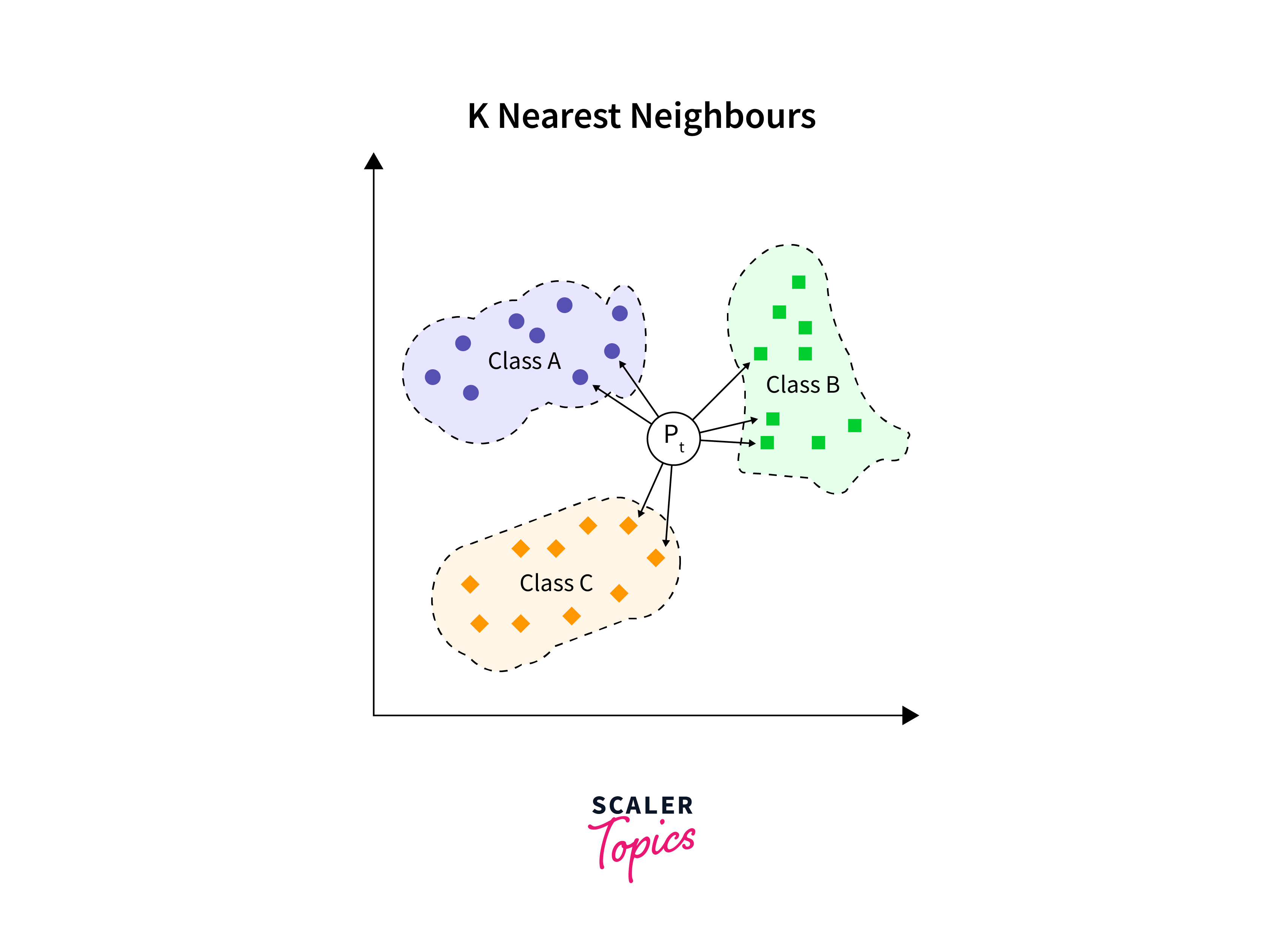
Decision Trees
Decision Trees are a non-linear predictive modeling approach used in both classification and regression tasks, where the goal is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features.
Understanding Entropy
Entropy is a bit like the "messiness" in a room full of toys, where each type of toy represents a class in multiclass classification in machine learning. If all the toys are mixed up, it's hard to find what you want, and the room (or dataset) is very "messy" or has high entropy. But if the toys are sorted into groups, it's much easier to find a specific toy, and the room is more organized, showing low entropy.
In multiclass classification, we use entropy to measure how mixed up our data is. Here's the breakdown:
- In terms of data, high entropy means the data is very mixed up, with lots of different classes jumbled together. Low entropy means the data is well sorted, with similar items (or classes) grouped together.
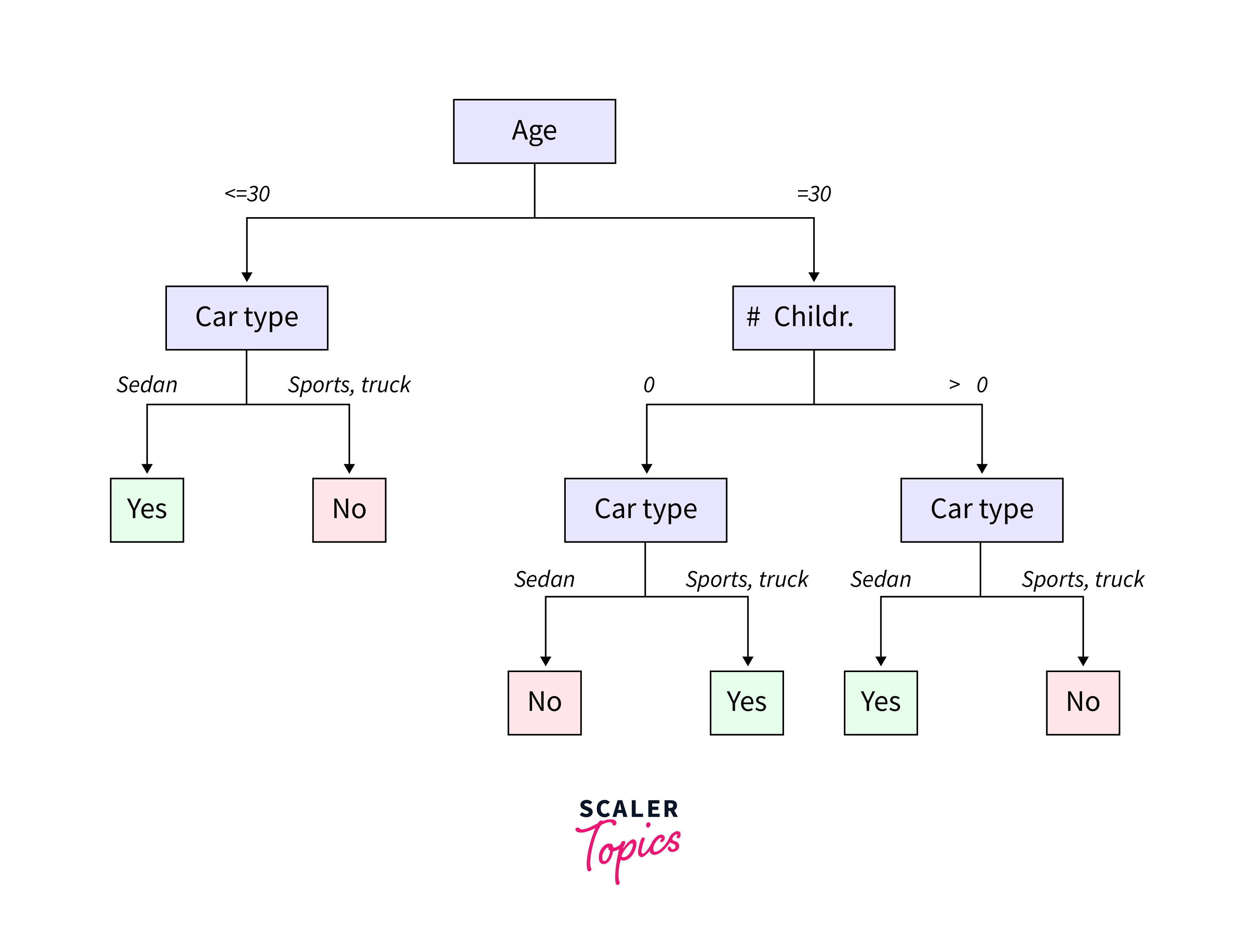
- When building a decision tree, we want to create branches based on features that make our data less "messy." We look at each feature and ask, "If I split my data based on this feature, will the groups be more organized?" Entropy helps us answer this by showing how much more organized (or less "messy") our data becomes after each split.
- In decision trees, we start with all our data at the top (like a messy room). Then, we choose a feature to split the data (like sorting toys by type). We pick the feature that reduces the "messiness" (entropy) the most. This means we end up with groups that are more alike (low entropy), making it easier to classify new data.
Formula:
The formula for entropy, which quantifies the disorder or uncertainty in a dataset, is given by:
KaTeX parse error: Expected 'EOF', got '₂' at position 25: …) = -∑ P(x) log₂̲ P(x)
Here, represents the dataset for which entropy is being calculated, is the probability of class occurring in the dataset, and the summation is over all classes in the dataset.
The Gini Index
The Gini Index, often used in multiclass classification in machine learning, is a measure that quantifies the impurity or purity of a dataset.Consider it a measure of the likelihood that an element, if randomly labeled based on the label distribution in the subset, would be mislabeled. In simpler terms, the Gini Index helps to understand how mixed a group is in terms of the different classes it contains.
In the context of multiclass classification in machine learning, a Gini Index of 0 is perfect, indicating that the set contains instances of only one class, making it completely pure. On the other hand, a Gini Index closer to 1 implies high impurity, meaning the set is a mix of instances from multiple classes. Decision tree algorithms, such as CART (Classification and Regression Trees), use the Gini Index to decide where to split the data.
Formula:
The formula for the Gini Index, a measure of impurity or purity used in decision trees is given by:
KaTeX parse error: Expected 'EOF', got '²' at position 29: … = 1 - ∑ [P(x)]²̲
Here, represents the dataset for which the Gini Index is being calculated, is the probability of class occurring in the dataset, and the summation is over all unique classes in the dataset.
Confusion Matrix for Multiclass Classification
A Confusion Matrix for Multiclass Classification in Machine Learning is a powerful tool used to visualize the performance of an algorithm. Unlike in binary classification, where the matrix has four components (True Positives, False Positives, True Negatives, False Negatives), a multiclass confusion matrix expands this concept to accommodate multiple classes.
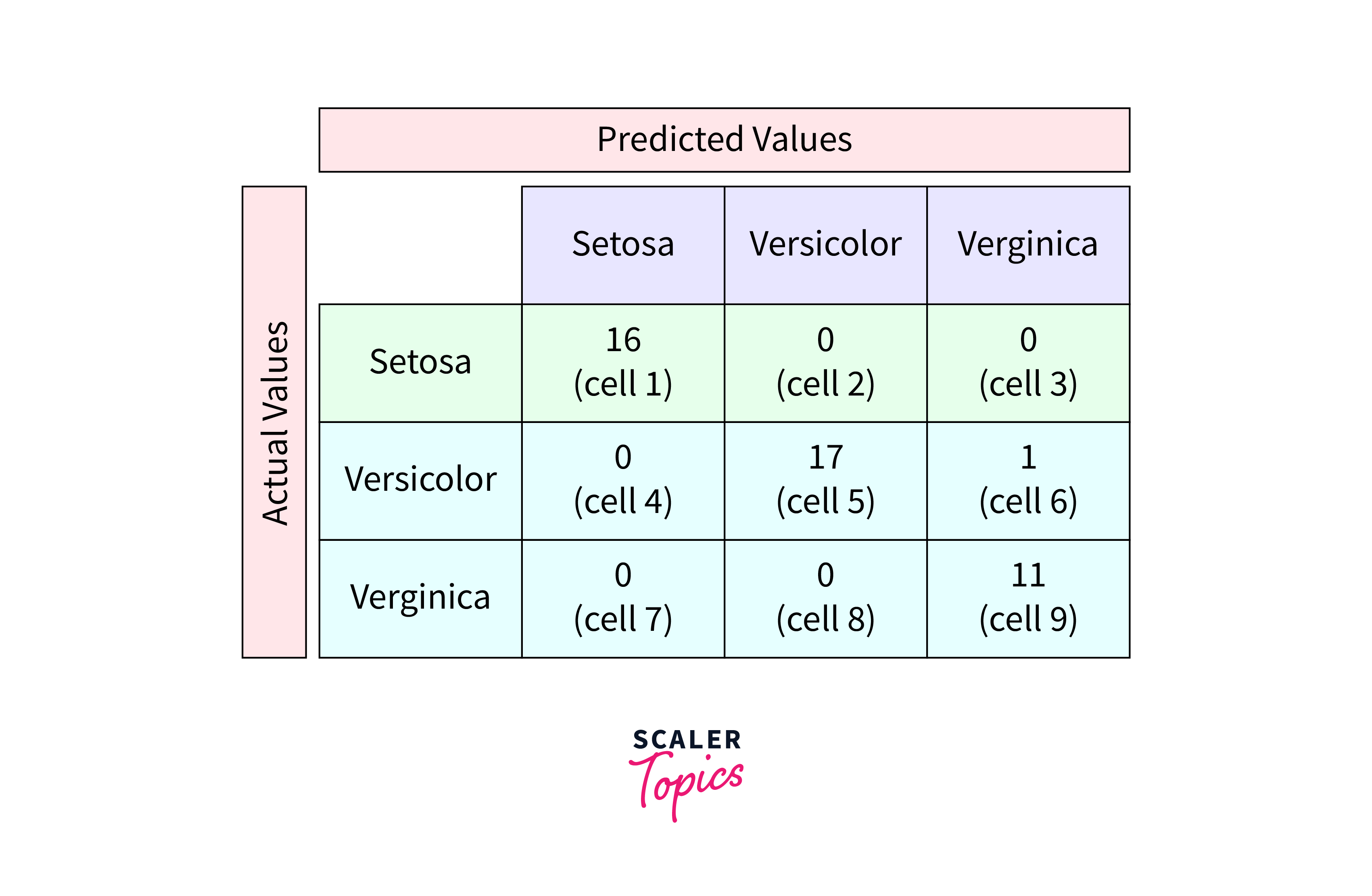 Imagine a classroom with students sorted into groups based on their answers to a question. Each group represents a predicted class, and the actual answers represent the true classes. The confusion matrix helps us see not only who was sorted correctly but also where mistakes were made.
Imagine a classroom with students sorted into groups based on their answers to a question. Each group represents a predicted class, and the actual answers represent the true classes. The confusion matrix helps us see not only who was sorted correctly but also where mistakes were made.
In a multiclass setting, the matrix is a square grid, where:
- Each row represents the instances in an actual class.
- Each column represents the instances in a predicted class.
- Each cell in the matrix shows the count of predictions for a pair of actual and predicted classes.
Multiclass Vs Multilabel
Here's a brief comparison between Multiclass and Multilabel classification:
| Feature | Multiclass Classification | Multilabel Classification |
|---|---|---|
| Definition | Each instance is assigned to one and only one class. | Each instance can be assigned to multiple classes. |
| Example | Classifying an animal as either a dog, cat, or bird. | Tagging a blog post with multiple topics like 'Technology', 'Innovation', and 'Education'. |
| Class Overlap | Classes are mutually exclusive; no overlap. | Classes can overlap; an instance can belong to multiple classes simultaneously. |
| Output Shape | Single label per instance. | Multiple labels per instance. |
| Use Case | Classifying types of fruits. | Categorizing news articles into various categories like 'Politics', 'Economy', 'Environment'. |
| Evaluation Metrics | Accuracy, F1-Score (macro/micro averaged), Precision, Recall | Subset Accuracy, Hamming Loss, F1-Score (sample/instance averaged) |
Binay Vs Multiclass Vs Multilabel
Here's a concise comparison between Binary, Multiclass, and Multilabel classification:
| Feature | Binary Classification | Multiclass Classification | Multilabel Classification |
|---|---|---|---|
| Definition | Involves two classes where each instance is assigned to one class. | Each instance is assigned to one and only one out of three or more classes. | Each instance can be assigned to multiple classes out of three or more. |
| Example | Email is either spam or not spam. | An image is categorized as either a cat, dog, or bird. | A movie can be tagged as action, comedy, romance, etc., and can have multiple tags. |
| Class Overlap | No overlap; an instance belongs to one of two classes. | No overlap; an instance belongs to one of multiple classes. | Classes can overlap; an instance can belong to multiple classes. |
| Output Shape | Single label with two possible values. | Single label, but with multiple possible values. | Multiple labels, each with a binary value. |
| Use Case | Determining if a transaction is fraudulent. | Classifying types of cuisines. | Categorizing a news article into various themes like sports, politics, etc. |
| Evaluation Metrics | Accuracy, Precision, Recall, F1-Score | Accuracy, F1-Score (macro/micro averaged), Precision, Recall | Hamming Loss, Precision@k, F1-Score (sample/instance averaged) |
Implementation of Mutliclass Classification using Python
Implementing multiclass classification in Python typically involves using libraries like scikit-learn, which provides a range of algorithms and tools for machine learning tasks.
- Data Preparation: Begin by importing your dataset and preparing it for training. This includes splitting the data into features (X) and labels (y), and further into training and testing sets.
- Choose a Model: Select a suitable algorithm for multiclass classification. Scikit-learn has several options, like RandomForestClassifier, KNeighborsClassifier, or SVC (Support Vector Classification).
- Train the Model: Fit the model to your training data.
- Make Predictions: Use the trained model to make predictions on your test data.
- Evaluate the Model: Assess the performance of your model using appropriate metrics. Scikit-learn provides a range of evaluation metrics suitable for multiclass classification, such as accuracy, precision, recall, and F1 score.
Conclusion
- There are multiple algorithms like Naive Bayes, KNN, and Decision Trees suitable for tackling multiclass classification problems, each with its unique approach and strengths.
- Understanding and utilizing the right evaluation metrics, such as the confusion matrix, accuracy, and F1-score, is crucial for assessing the performance of multiclass classification models accurately.
- Concepts like entropy and the Gini index play an important role in the decision-making processes of certain algorithms, highlighting the importance of a strong theoretical foundation in effectively applying machine learning techniques.
- It's important to distinguish multiclass classification from binary and multilabel classification, as each comes with its own set of challenges and methodologies.
- Python and libraries like scikit-learn provide powerful and accessible tools for implementing multiclass classification, making it possible to apply these concepts to real-world problems efficiently.
