Computational Desiderata for Representations

Overview

Meaning representations are the meanings of linguistic utterances (sentences) that can be captured in formal structures. When the necessary type of semantic processing is not made possible by raw linguistic inputs or structures, meaning representations are required. The computational desiderata for meaning representations are - verifiability, unambiguous representations, canonical form, inferences and variables, and expressiveness.

Introduction

What does the word "desiderata" mean? The word desiderata means "something that is wanted or needed". In this article, we're going to talk about computational requirements for representations in natural language processing. Now what do we refer to when we say representations? Well, here we are talking about meaning representations. The meaning of linguistic utterances (or, sentences) can be captured in formal structures are meaning representations. And, correspondingly, the frameworks that are used to specify the syntax and the semantics of these representations are meaning representation languages.

The process of creating representations of everyday common-sense knowledge of the world and then assigning it to linguistic inputs is called semantic parsing. Another term we must make ourselves familiar with is computational semantics which is the entire enterprise of designing these meaning representations and the associated semantics parsers.

Moving on, when the necessary type of semantic processing is not made possible by the raw linguistic inputs or any of the structures that can be derived from them by any of the transducers, meaning representations are required. To complete activities requiring the meaning of linguistic inputs, we specifically require representations that connect linguistic inputs to the non-linguistic knowledge of the outside world. To demonstrate this idea, have a look at the following common language activities that demand semantic processing of natural language in some way:

Answering essay questions in exams
Deciding what to order at a restaurant by reading a menu
Learning to use new software referencing a manual
Following a recipe, etc.

Let us look at an example of meaning representations. Let's say we have a sentence: "I have a car". Here's what a meaningful representation of this sentence would look like:

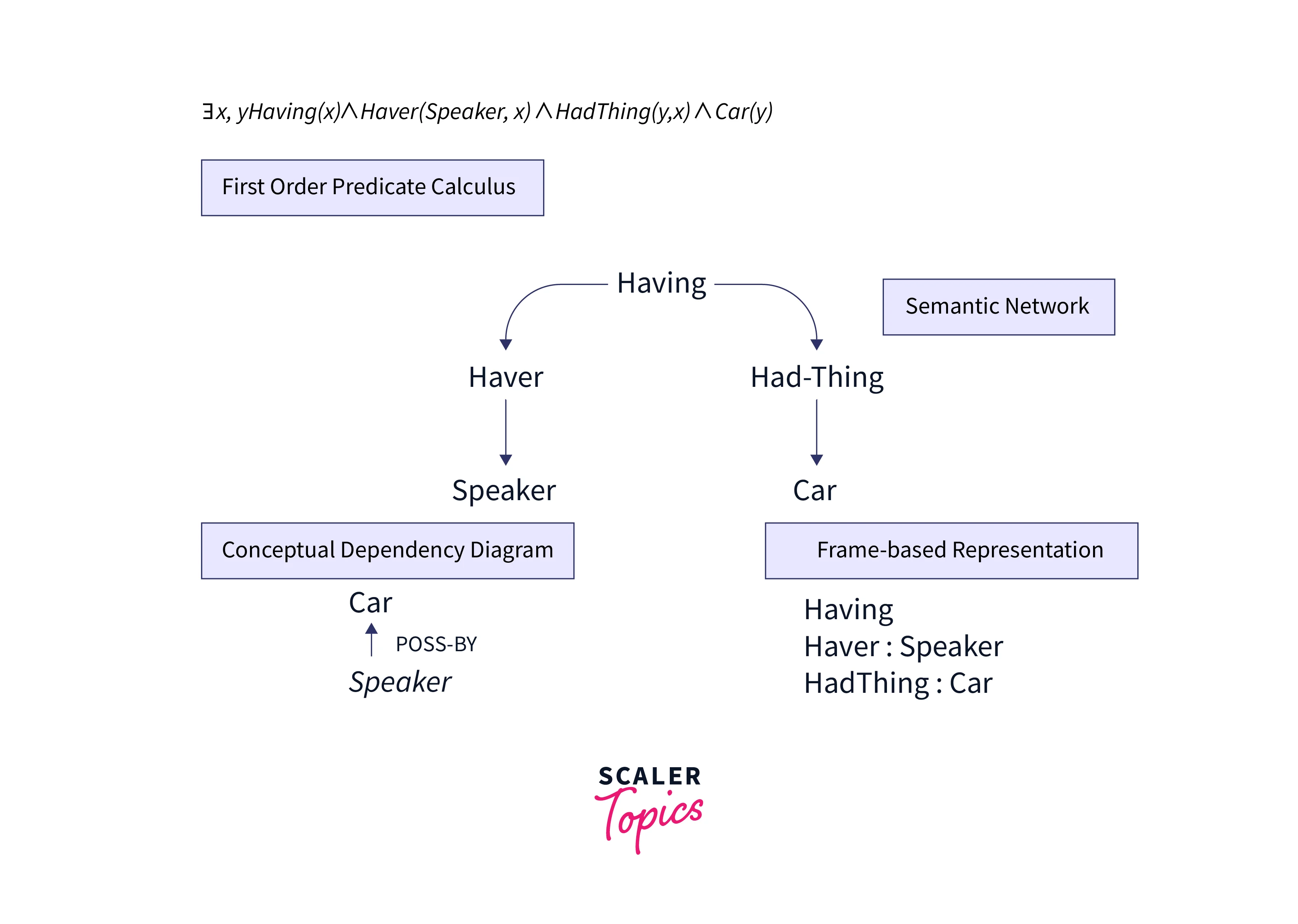
computational-data-in-nlp

This image shows some examples of meaningful representations of the sentence "I have a car", such as first-order predicate calculus, the conceptual dependency diagram, and frame-based representation. All these representations share the notion that is meaning representations consist of structures that are composed of a set of symbols or representational vocabulary. When these symbol structures are appropriately arranged, they are taken to correspond to objects, properties of objects and relations between objects, and so on.

Now that we have covered an introduction let's get to the desiderata for meaning representations or the kind of computational data in NLP. We will talk about the meaning of representations that will provide correspondence to the state of affairs being represented.

Desiderata for Meaning Representations

Let's think about the requirement for meaningful representations and what they should accomplish for us. Let's use a system that recommends restaurants to travelers based on a knowledge base to focus this conversation.

Verifiability

Take the example of the following question:

Does Maharani serve vegetarian food?

Knowing what this question is asking and determining whether the verifiability it is requesting of Maharani is necessary to respond to it.

The ability of a system to make comparisons between the state of affairs given by a representation and the state of affairs in some world as represented in a knowledge base is known as verifiability.

For instance, we'll require a representation like Serves(Maharani, VegetarianFood) that a system may compare against its database of knowledge about specific restaurants, and if it discovers a representation matching this proposition, it can respond with a positive. If not, it must either respond "No" if it knows all the nearby eateries or "I don't know" if it is aware that its information is incomplete.

Unambiguous Representations

Semantics is ambiguous, just like the other fields we have studied. In various contexts, words and sentences can have multiple meaning representations. Think about the following utterance:

I want to eat someplace that's close to IIT.

This statement could refer to the speaker's desire to dine at a nearby establishment or, in the case of Godzilla speaking, the speaker's desire to consume a neighboring establishment. A single linguistic expression can have one of two interpretations, making the sentence ambiguous. However, our representations of meaning cannot be vague.

Any ambiguity in the meaning of an input should be removed from the representation so that the system can reason over a representation that can only mean one of two things to choose how to respond. Here comes in vagueness.

Vagueness, which occurs when a meaning representation leaves some aspects of the meaning unexplained, is a term strongly connected to ambiguity. There are no different representations that result from vagueness.

Think about the following utterance:

I want to eat Italian food.

Italian cuisine may offer sufficient details to make recommendations, but it is still unclear as to what the user wants to eat. For some purposes, a general interpretation of this phrase's meaning might be suitable, but for other purposes, a more precise interpretation might be required.

Canonical Form

According to the idea of canonical form, different inputs with the same semantic content should have the same semantic representation. Since systems only need to deal with a single meaning representation for a potentially vast range of expressions, this method considerably simplifies reasoning.

Think about the following substitutions for the phrase:

Does Maharani have vegetarian dishes?
Do they have vegetarian food at Maharani?
Are vegetarian dishes served at Maharani?
Does Maharani serve vegetarian fare?

We want these alternatives to map to a single canonical meaning representation even though they employ various terms and syntax. The majority of the representations wouldn't line up if they were all different, assuming the system's knowledge base only has one representation of this information. Naturally, we could record every potential alternative representation of a given fact in the knowledge base, but doing so would make maintaining the knowledge base extremely complex.

Canonical form indeed makes semantic parsing more difficult. Since having and serving are comparable in this context, and all of these parse structures still result in the same meaning representation, our system must conclude that vegetarian food, vegetarian dishes, and vegetarian fare all refer to the same thing. Or, think about these two instances:

Maharani serves vegetarian dishes.
Vegetarian dishes are served by Maharani.

A system must nonetheless assign Maharani and vegetarian foods to the same roles in the two examples despite the varied location of the arguments to serve. To do this, it must call on grammatical knowledge, such as the relationship between active and passive sentence forms.

Inferences and Variables

What about more complex requests such as:

Can vegetarians eat at Maharani?

There is a relationship between what vegetarians consume and what vegetarian restaurants serve, therefore, this request receives the same response as the others—not because they mean the same thing. This is a universal truth. In a knowledge base, we must link the semantic representation of this request with this fact about the outside world.

The ability to employ inference to arrive at reliable conclusions based on the meaning representation of inputs and its prior knowledge must be had by a system.

The system must be able to infer truths about propositions that are logically derived from those that are explicitly stored in the knowledge base but are not explicitly represented there.

Now consider the following somewhat more complex request:

I’d like to find a restaurant where I can get vegetarian food.

The user wants details about an unidentified restaurant that serves vegetarian food; the request makes no mention of any specific eatery. Since there are no specific eateries mentioned, simple matching will not succeed. Variables must be used to respond to this request using a representation like the one shown below:

$Serves(x,VegetarianFood)$

Only when the variable x can be substituted with an item from the knowledge base in such a way that the full proposition then matches does matching succeed. The user's request can then be fulfilled using the idea that was used in place of the variable.

Any meaning representation language must be able to handle these types of indefinite references to function properly.

Expressiveness

A meaning representation scheme must, in theory, be expressive enough to accommodate any comprehensible natural language speech. First-Order Logic, as explained in Section 19.3, is expressive enough to handle a significant portion of what has to be represented, even though this is likely too much to anticipate from any one representational system.

You are now aware of all the computational requirements for meaning representations in natural language processing.

Conclusion

Desiderata means something that is wanted or needed. The meaning of linguistic utterances (or sentences) can be captured in formal structures are, meaning representations.
We understood the computational requirements or the desiderata for meaning representations are Verifiability, Unambiguous Representations, Canonical Form, Inference and Variables, and Expressiveness.