lda2vec – deep learning model

Introduction

In many of the use cases, it is very important to understand the theme of a document or a topic that is being referred to in that document. Take an example where you were given some news articles and asked to identify the events being talked about in these articles; it could be a sports event or the election, or any other event. There could be a varying number of events happening around the world, and it's very hard to put them in a fixed set of categories. With that intention, there are no predefined categories are labels associated with these news articles. This needs to have a way to identify the latent themes or topics of the documents. Learning this latent theme (or abstract topic) in Natural Language Processing (NLP) is called Topic Modelling.

Topic models are based on the basic assumptions:

• Each document (D) is a mixture of topics (T), and
• Each topic (T) is a mixture of words (W).

In other words, a topic is a hidden theme that can be described by certain words means there is an association between a topic and a certain set of words. Documents contain words that can be divided into multiple-word groups. The assigned topic can be attached to the document using these word groups. In this way, a document becomes a mixture of topics.

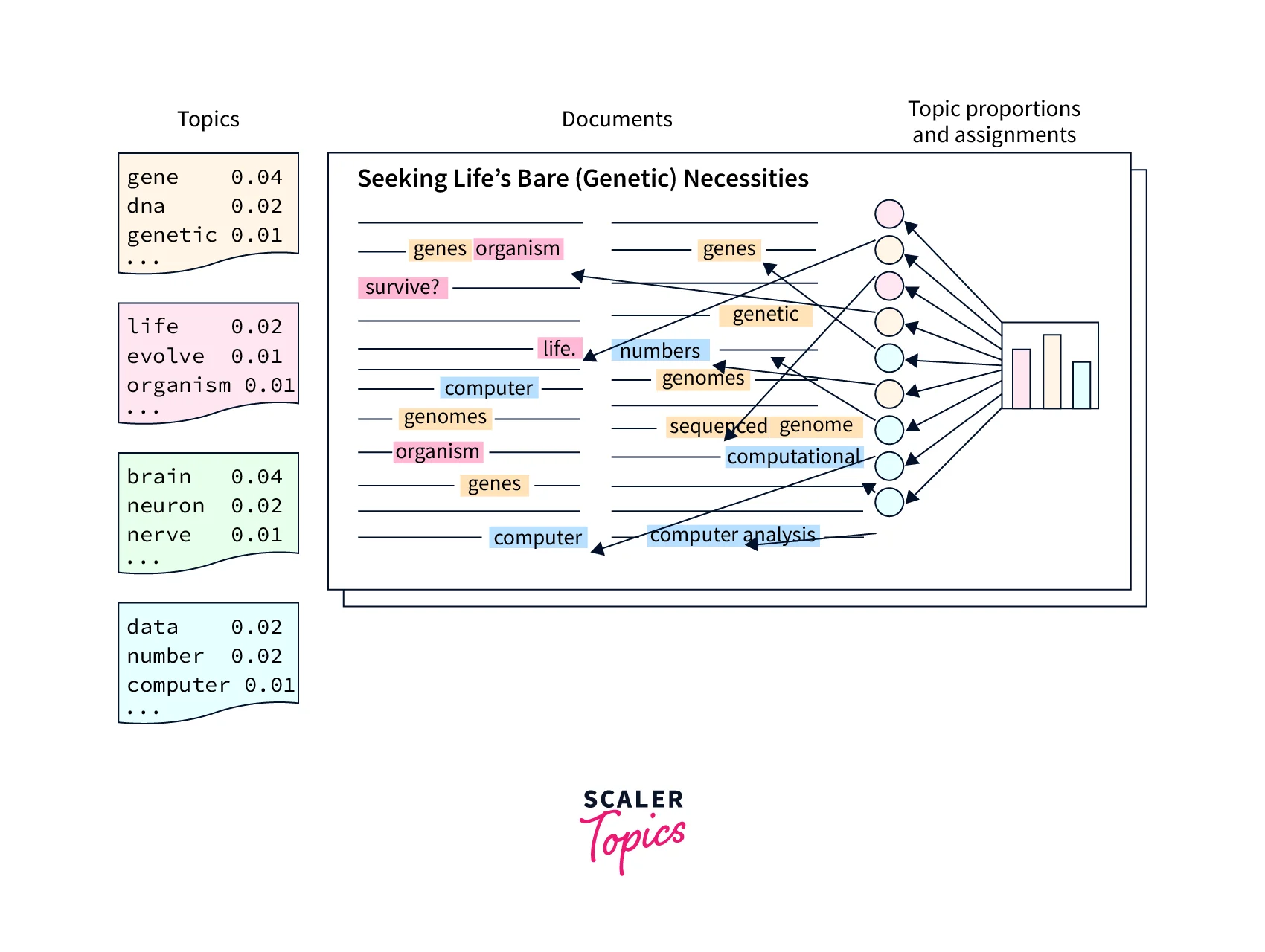
Topic models are very useful for document clustering, organizing large blocks of textual data, information retrieval from unstructured text, and feature selection.

LDA is a popular topic modeling approach that uses a prior Dirichlet distribution to discover the topic distribution in a corpus and the matching word distributions inside each topic.

LDA (Latent Dirichlet Allocation)

Latent Dirichlet Allocation (LDA) has these underlying assumptions:

1. Similar topics make use of similar words and
2. A documents contain multiple topics.

LDA assumes that the distribution of topics in a document and the distribution of words in topics are Dirichlet distributions. To map the documents to a list of topics, LDA assigns topics to arrangements of words; for example: 'mobile phone' can be assigned to the topic 'electronics'. LDA treats documents as bags of words. It also assumes that all words in the document can be assigned a probability of belonging to a particular topic.

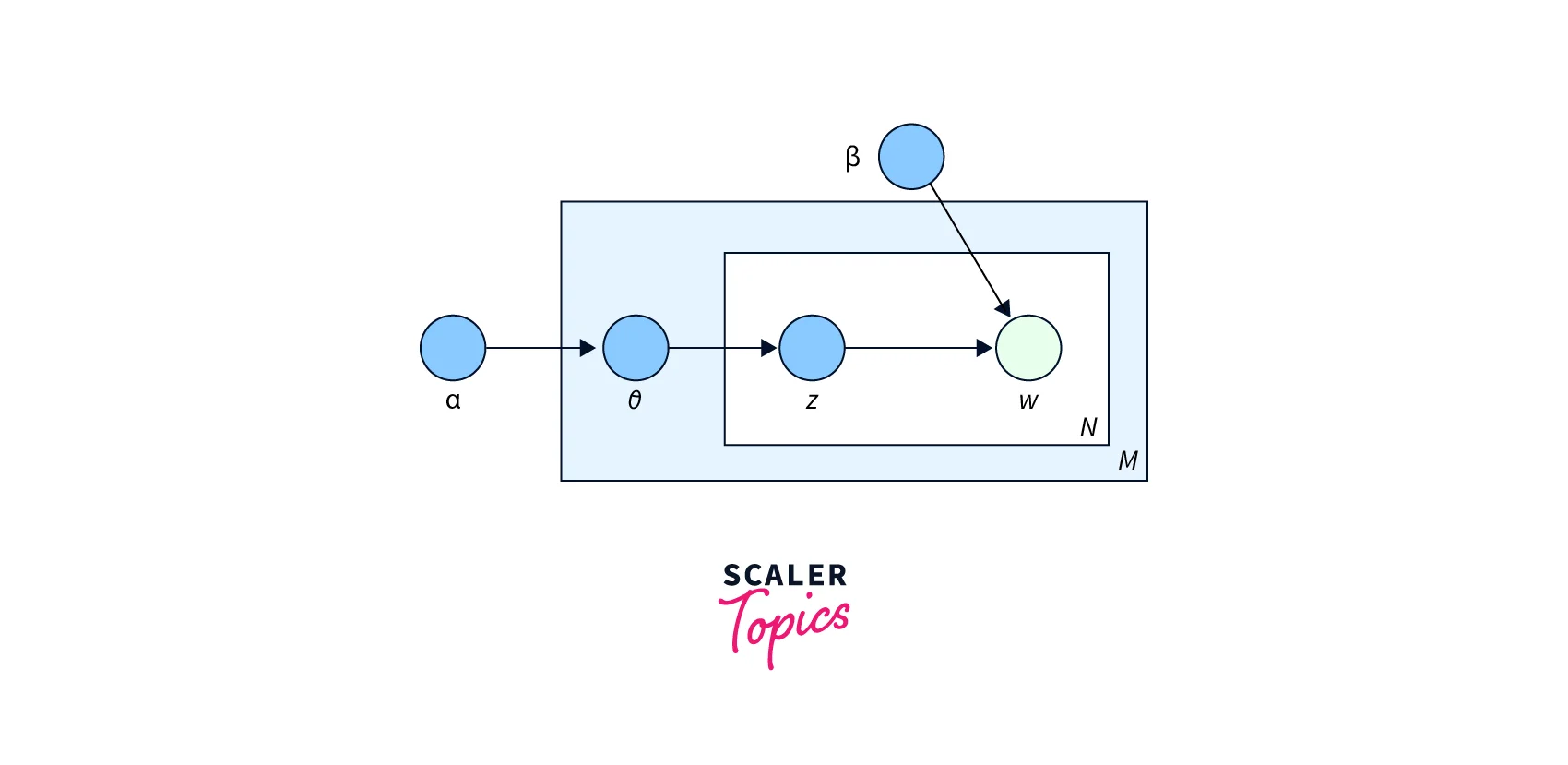
Two hyperparameters control document and topic similarity, known as alpha and beta, respectively. A low value of alpha will assign fewer topics to each document, whereas a high value of alpha will have the opposite effect. A low value of beta will use fewer words to model a topic, whereas a high value will use more words, thus making topics more similar between them. A third hyperparameter has to be set when implementing LDA, namely, the number of topics the algorithm will detect since LDA cannot decide on the number of topics by itself.

LDA outputs a vector of probabilities that contains the coverage of every topic for the document being modeled, something like [0.2, 0.5, 0.2, 0.1] where the first value shows the probability or coverage of the first topic, and so on.

For more information, you can refer to the original LDA paper.

Word Embeddings

What are Word Embeddings?

Since almost all machine learning algorithms work on mathematical equations containing variables that need information represented as numbers. Before applying any kind of machine learning algorithm for information extraction, these words need to be converted to a numerical representation like an array of numbers. This array of numbers is called embedding or vector representation of a word. Each word is mapped to a vector something like:

barack = [1, 0, 0, 0, 0] obama = [0, 1, 0, 0, 0] was = [0, 0, 1, 0, 0] the = [0, 0, 0, 1, 0] president = [0, 0, 0, 0, 1]

In recent times, the two most popular techniques for generating word embeddings are word2vec and GloVe. We briefly talk about word2vec.

What is Word2vec?

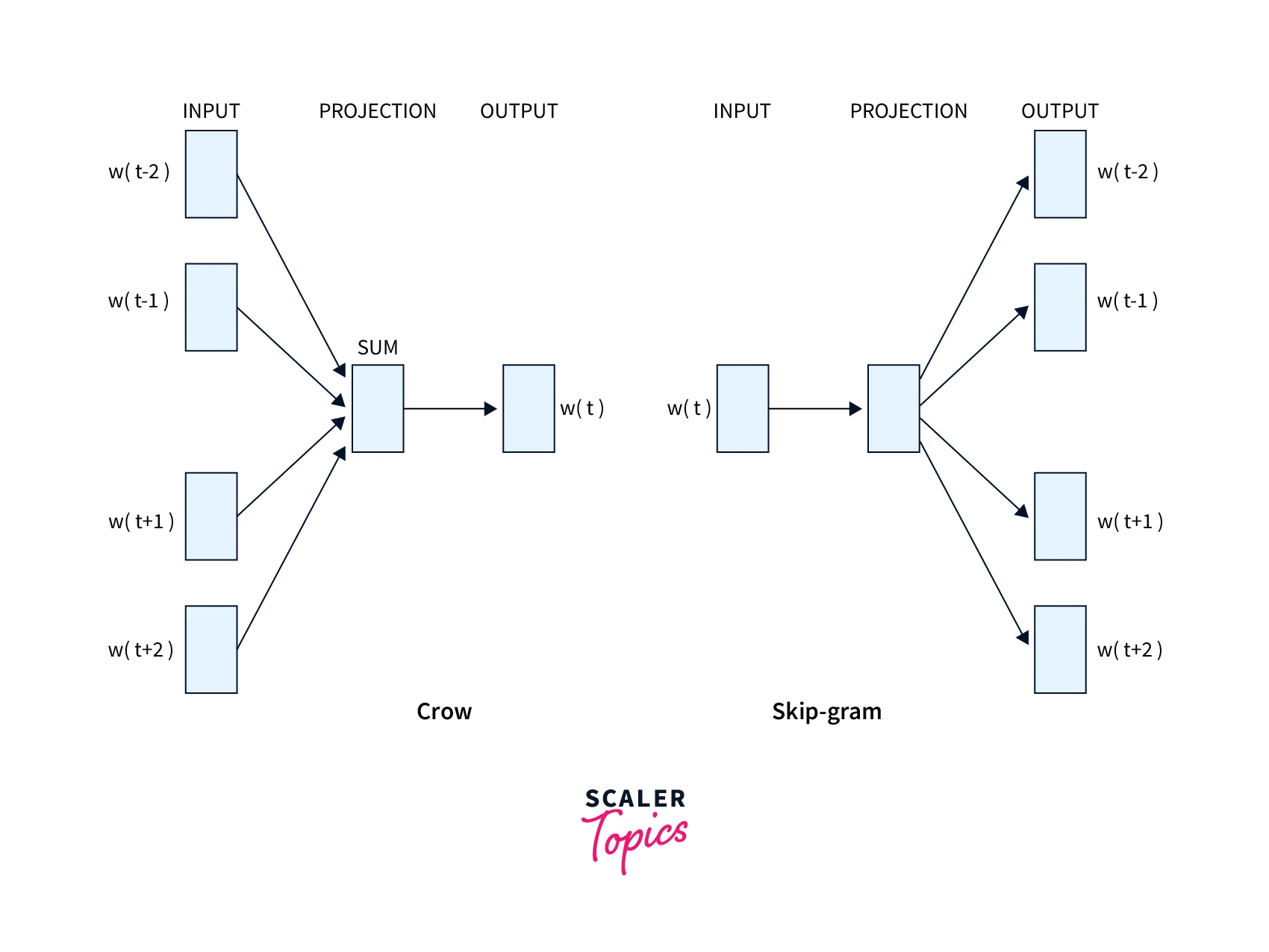
Word2Vec is an idea presented by Tomas Mikolov et al. from Google, where word representation or embeddings can be learned from neighbors. Neighbors provide information about the usage of the word. Word2vec works on the idea of learning from the surrounding words in a window of words. This can be done in two ways: 1. Skip-gram and 2. Continuous bag of words (CBOW)

Skip-Gram and CBOW

The main difference between Skip-gram and CBOW is the way they learn and predict the words. Skip-gram learns the word representation by predicting the neighbors from the word, and CNOW by predicting the word from the neighbors.

What is Lda2vec?

LDA and word2vec are both very useful, but LDA uses global context with words and documents and Word2Vec local context (neighboring words). An LDA vector is so sparse that the users can interpret the topic easily, but it is inflexible. Word2Vec’s representation is not humanly interpretable but easy to use. lda2vec, which is a hybrid of the two, to get the best out of the two algorithms. lda2vec, a model that learns dense word vectors jointly with Dirichlet-distributed latent document-level mixtures of topic vectors.

lda2vec builds representations over both words and documents by mixing word2vec’s skip-gram architecture with Dirichlet-optimized sparse topic mixtures. In the original skip-gram method, the model is trained to predict context words ('jumped,' 'over') based on a pivot word ('fox'). In lda2vec, the pivot word vector and a document vector are added to obtain a context vector. This context vector is then used to predict context words.

lda2vec Architecture

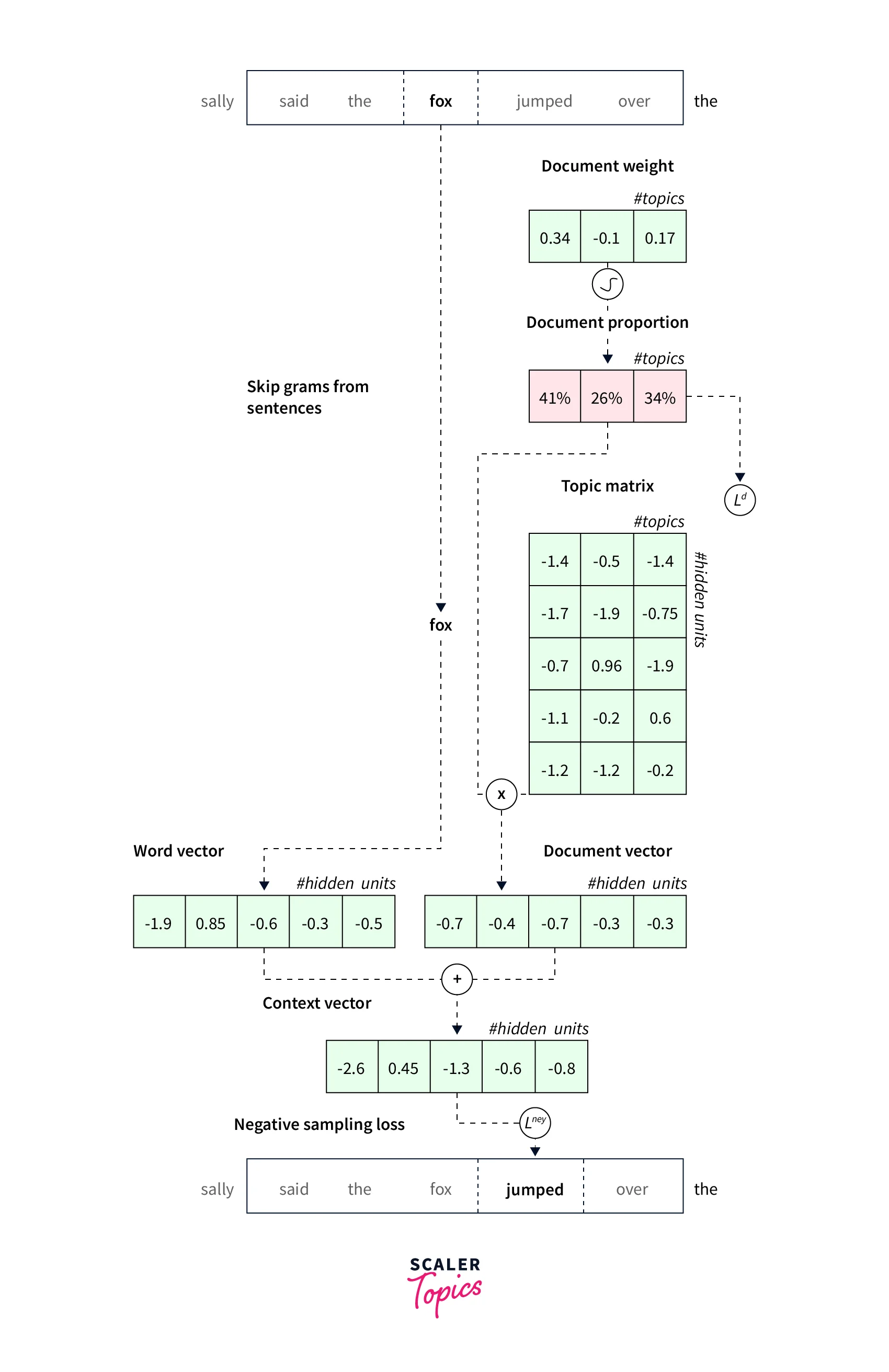
A document vector is decomposed into a topic matrix and a document weight vector, much to the LDA model. The topic matrix is made up of several topic vectors, whereas the document weight vector shows the percentage of the various topics. Thus, a context vector is created by fusing the several topic vectors that appear on a page.

Let's look at the next example, which is depicted in Figure 5, where the article discusses various airlines. According to the word2vec model, if the pivot word is "German," potential context words include "French," "Dutch," and "English," presuming that it is a spoken language. These would be the most logical hypotheses in the absence of any global (document-related) knowledge.

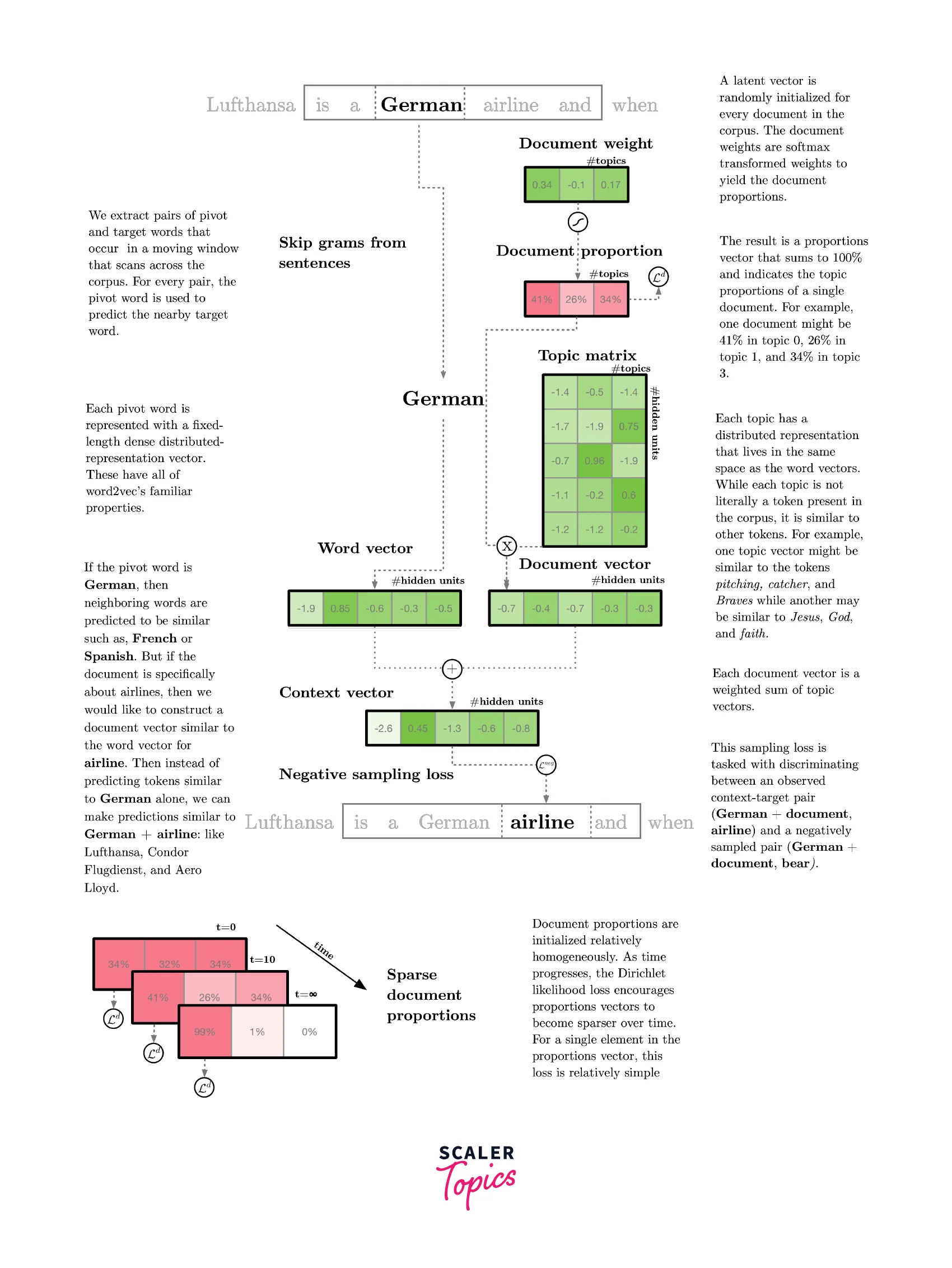
In the lda2vec model, context words can be more accurately predicted by including an additional context vector coming from the LDA topic model.

Note that these topic vectors are learned in word space, which allows for easy interpretation: you simply look at the word vectors that are closest to the topic vectors. In addition, constraints are put on the document weight vectors to obtain a sparse vector (similar to LDA) instead of a dense vector. This enables easy interpretation of the topic content of different documents.

In short, the end result of the lda2vec is a set of sparse document weight vectors and easily interpretable topic vectors.

Although the performance tends to be similar to traditional LDA, using automatic differentiation methods makes the method scalable to very vast datasets. In addition, by combining the context vector and word vector, you obtain specialized word vectors, which can be used in other models (and might outperform more generic word vectors).

Let's talk a little about code. Defining the lda2vec model is easy; here's how it's done:

To visualize your results, you can make use of pyLDAvis in the following way:

lda2vec Official Resources

• Official Github:
• Official Python Package: