Non-Negative Matrix Factorization

What is Non-negative Matrix Factorization, and Why Do We Need NMF?

NMF is an unsupervised feature extraction algorithm for factorizing a data matrix subject to constraints where the resulting factors possess different but useful representational properties.

The central principle in Non-negative matrix factorization is that given a non-negative matrix V, we shall find non-negative matrix factors W and H such that V ≈ W*H.

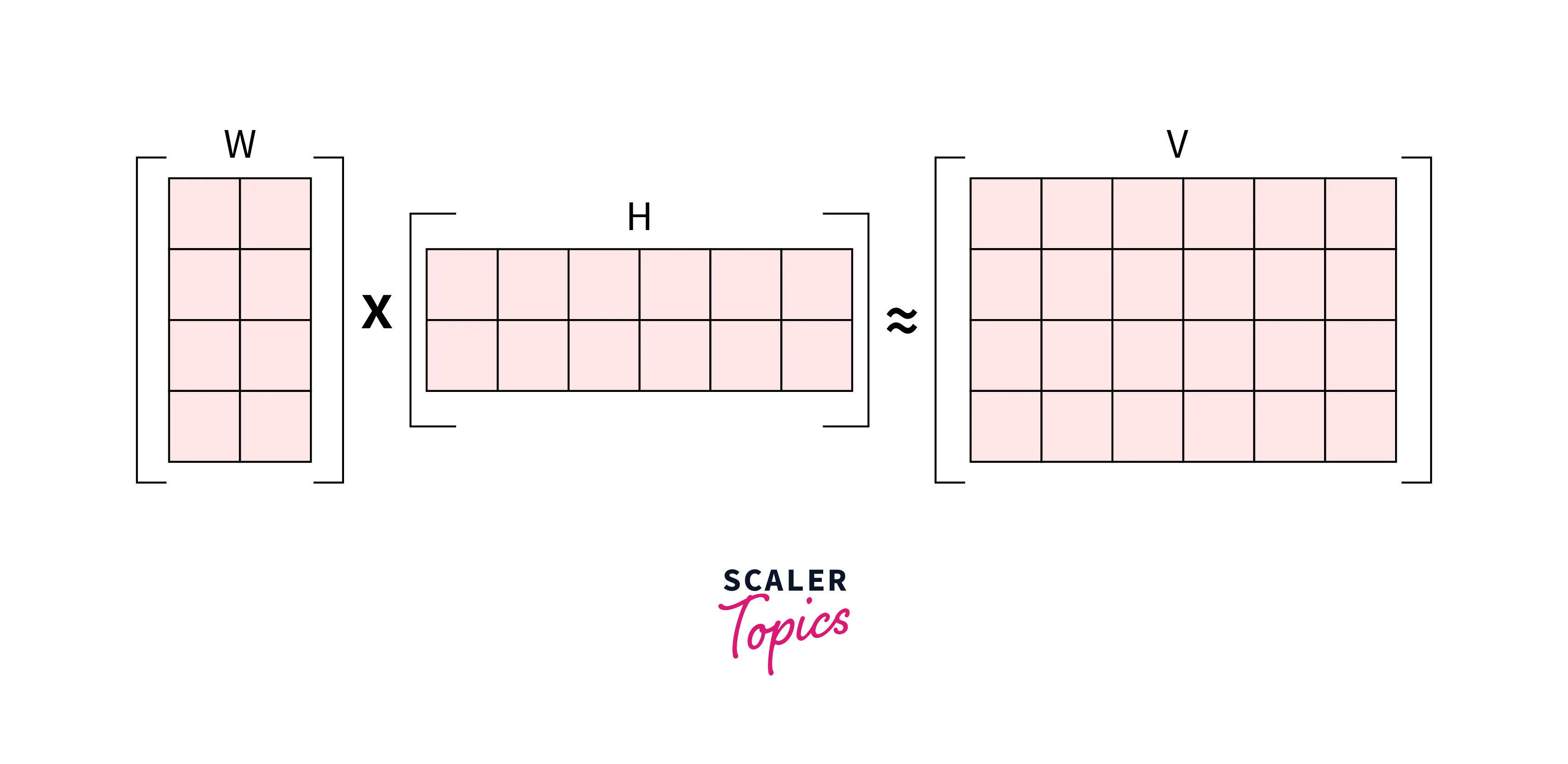
Let us see why we do need an algorithm like NMF when many other decomposition techniques are available for matrix factorization.

Data is often nonnegative when captured from many natural processes like pixel intensities, food or energy consumption, stock market values, and many such cases.

• We may need to optimally process such data under nonnegativity constraints for the sake of interpretability of the results and handle sparsity induced by nonnegativity.
• NMF is suitable for such cases and multiple problem statements related to decomposition, matrix factorization, and finding latent structure in data.

Components of NMF

The main components of Non-negative matrix factorization are the feature matrix and the coefficient matrix.

• Feature Matrix (W):
  This is the matrix W which can be regarded as containing a basis that is optimized for the linear approximation of the data in V.

  • As we represent the many initial data vectors with few basis vectors, this will ensure a good approximation is reached only if the basis vectors discover a structure that is latent in the data.

• Coefficient Matrix (H):
  This matrix contains the weights associated with matrix W.

  • The hidden features in the input matrix are assumed to be represented by each column of the W matrix.
  • Each column in the H matrix represents the coordinates of each representative data point in the matrix W.

  

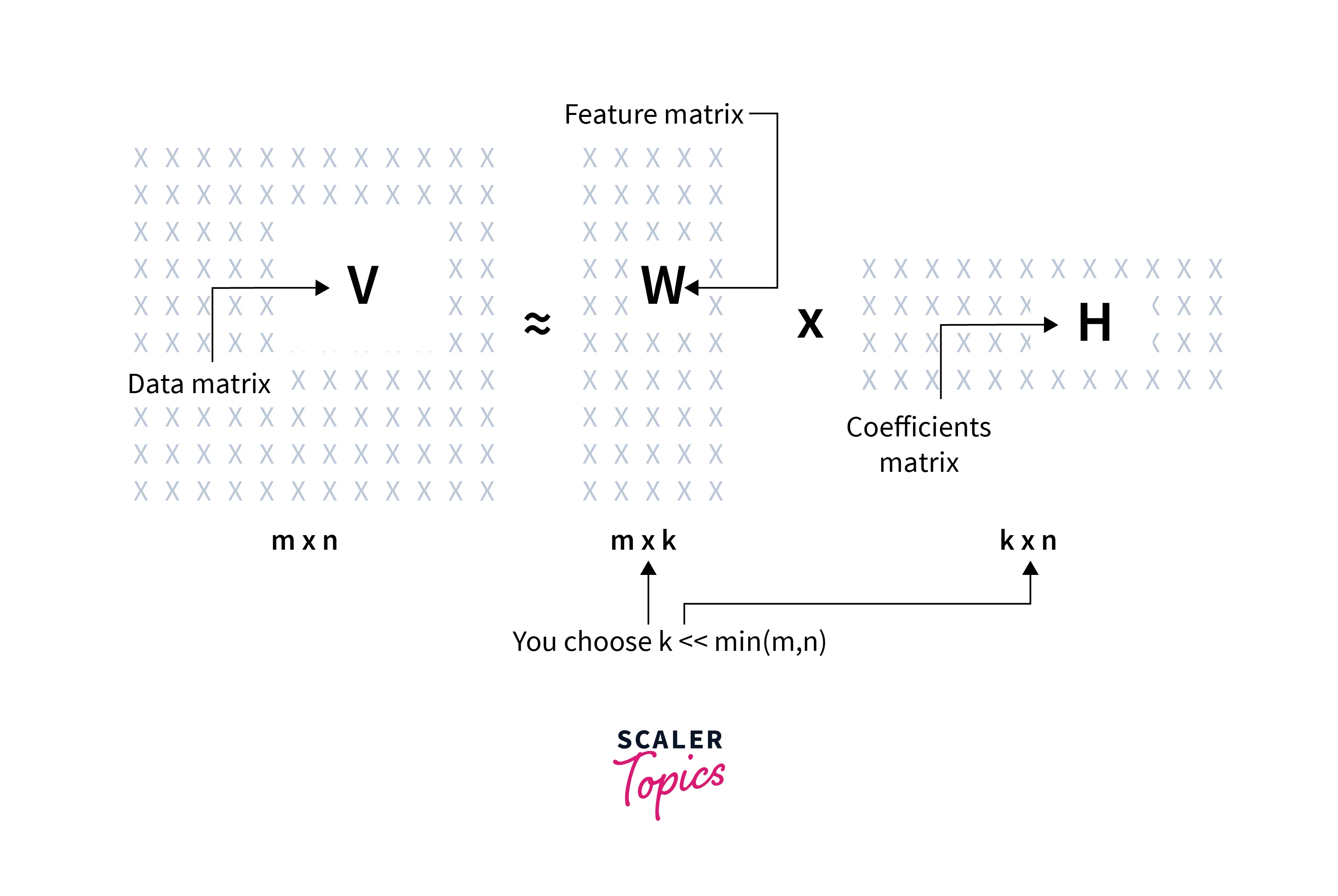
  Hence each data point represented as a column in the V matrix can be approximated by an additive combination of the non-negative vectors represented as columns in W in Non-negative matrix factorization.

Why Does Non-negative Matrix Factorization Work? The Intuition

We have the input matrix (V) as the combination of multivariate n-dimensional data vectors where the vectors are placed in the columns of an $m x n$ matrix V where m is the number of examples in the data set.

The problem is to approximately factorize V into an $m x k$ feature matrix W and an $k x n$ co-efficient matrix H using Non-negative matrix factorization.

Typically r is chosen to be smaller than n or m, so that W and H are smaller than the original matrix V, resulting in a well-compressed version of the original data matrix.

Image Processing

Non-negative matrix factorization can be used to compress images and summarise the pixes in image processing tasks. When dealing with images of greyscale, we can represent pixels as a vector of values. For a dataset with multiple images like the face,s we can represent the pixels as a matrix where each column represents an image and rows as pixels.

NMF can decompose the matrix into two submatrices W and H where the columns of W can be interpreted as images (the basis images), and H can be used to sum up the basis images to reconstruct an approximation to a given face.

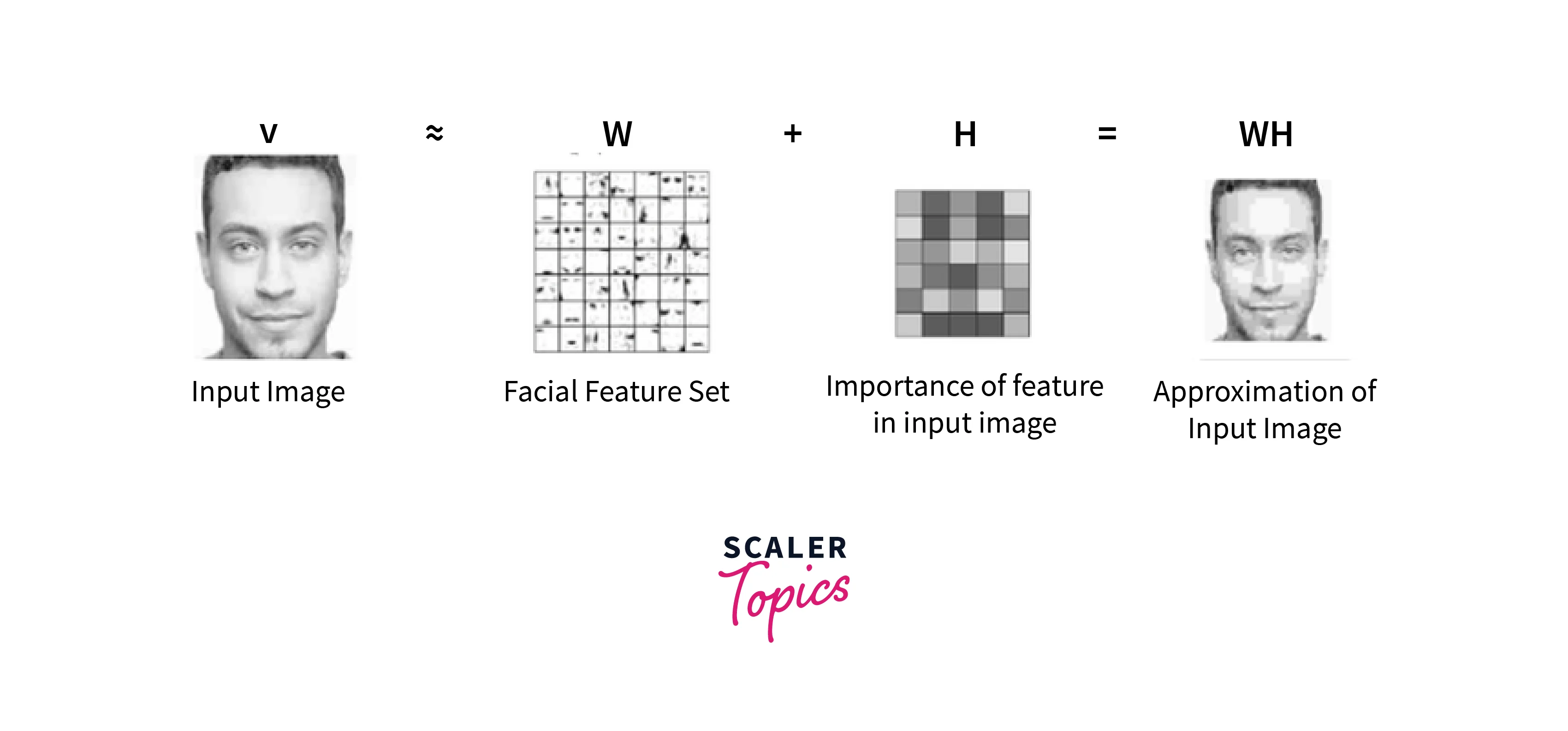
• For the example of facial images, the matrix W with basis images is the features present in each image like eyes, noses, mustaches, and lips.
• On the other hand, the columns of H indicate which feature is present in which image from the decomposition using the Non-negative matrix factorization.

Text Mining

In the text mining domain also, when the text corpus has a large number of documents, Non-negative matrix factorization can be used to discover topics and classify the documents among automatically identified hidden topics.

The text corpus can be represented with a document term matrix as a bag-of-words matrix where each row corresponds to a word and each column to a document as a feature.

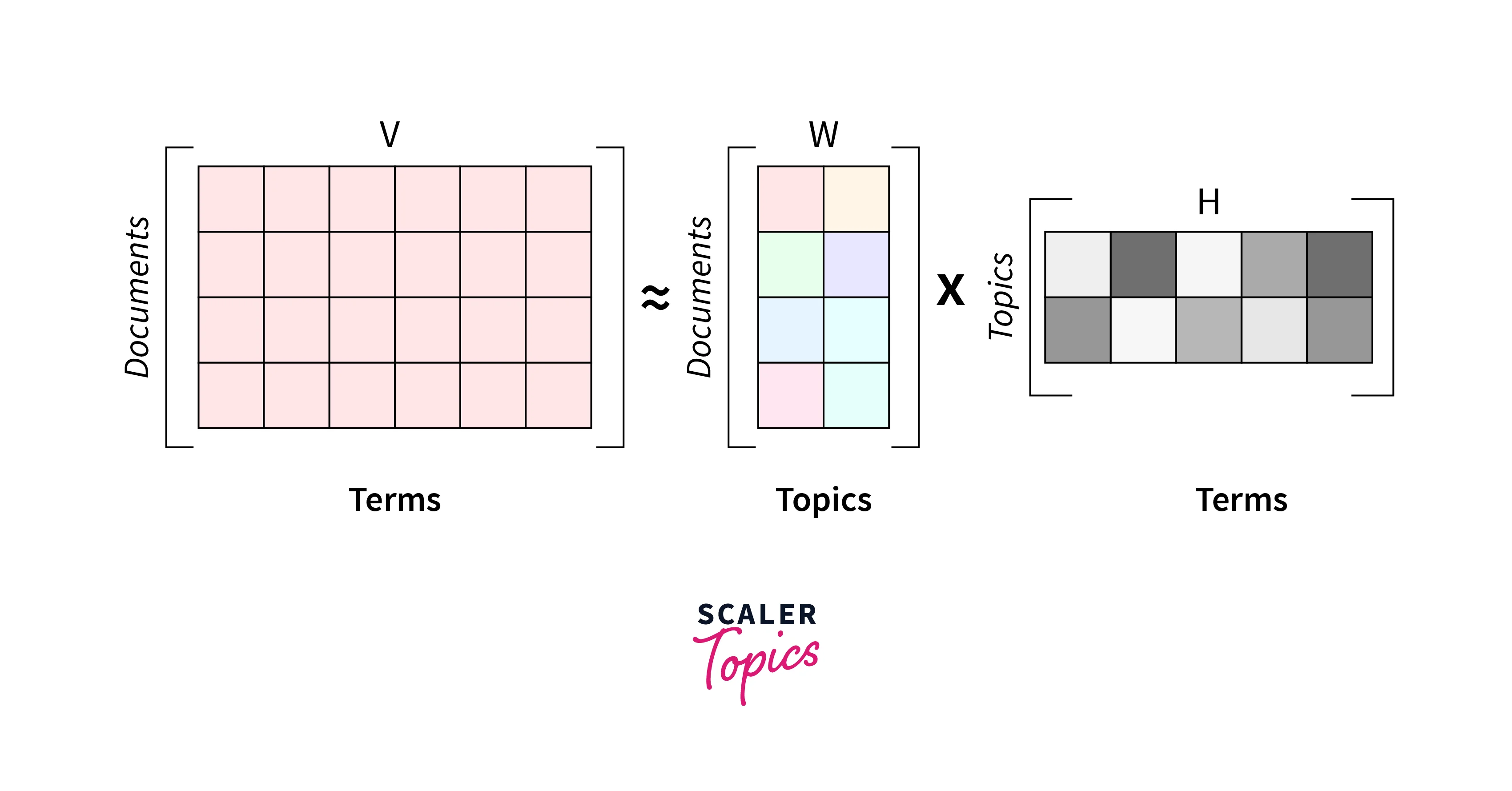
• When we utilize the NMF technique for the decomposition of text corpus, it will generate a usual combination of two matrices, W and H:
• The columns of W can be interpreted as topics (like basis documents in image processing) with sets of words found simultaneously in multiple documents.
• The other decomposed matrix, H gives contributions from different topics to reconstruct the word mix of a given original document so that we can multiply both matrices to find similarities.

Hyperspectral Unmixing

Non-negative matrix factorization can be used with hyperspectral images to compute the spectral signatures of the endmembers (things like grass, roads, metallic surface,s, etc. are endmembers) and combinedly the abundance of each endmember in each pixel.

• Hyperspectral images typically have 100 to 200 wavelength-indexed bands showing the fraction of incident light being reflected by the pixel at each of those wavelengths.
• When we have a set of hyperspectral images, we will want to identify the different materials present as end members in the images.
• Once the end members are identified, we want to know which of them are present in each pixel, along with their proportions.

Non-negative matrix factorization will produce two matrices, W and H. The columns of W can be interpreted as basis endmembers. H tells us how to sum contributions from different endmembers to reconstruct the spectral signal observed at a pixel.

Data Preparation for Non-negative Matrix Factorization

• We need to ensure that all the numerical attributes used in the feature matrix are normalized before running Non-negative matrix factorization.

  • The normalization of the input matrix is reported to achieve faster convergence* of the algorithm (in multiple folds) when compared to nonscaled versions.
  • It is also seen that without proper normalization of the input matrix, the columns of W and the rows of H are not comparable after decomposition since they are not standardized, which results in interpretation problems when using decomposition results.
  • Since the decomposition (of original matrix V into individual components W and H) doesn't have a definite solution (we are trying to approximate the multiplication output matrices to be almost equal to the input matrix), if the columns values of V have different scales, it may lead to unstable solutions each time we run the algorithm in iterations leading to downstream problems.

• Typical normalization scheme followed: Feature scaling is applied to the original data matrix V - each of the p rows of V is normalized to have values between 0 and 1.

• Treatment for missing values:

  • We can replace the missing categorical values with the mode.
  • All the missing values in numerical values can be imputed with mean or median.
  • If there is any sparse numerical data, it can also be imputed with zeros and sparse categorical data with zero vectors.

• If we are dealing with text data like in topic modeling using Non-negative matrix factorization, we need to clean and pre-process the data (tokenization, stop word removal, stemming, BOW representation) and can also create features using some method like tf-idf.

Implementing Non-negative Matrix Factorization

Let us implementNNNNonnegativematrix factorization using sklearn for topic modeling in an inbuilt sample dataset in sklearn.

Tuning the Non-negative Matrix Factorization Algorithm

• The main parameters relevant to running Non-negative matrix factorization in typical libraries are the following:

  • n_components:
    Equivalent to the number of topics or features, this has to be given to the algorithm and can be tuned
  • max_iter:
    The number of iterations to run the optimization algorithm defaults to 200 in sklearn
  • Convergence tolerance:
    Tolerance of the stopping condition, defaults to .05 in sklearn

• For tuning the parameters, we can set up a grid-search and run with an external loss function like coherence score or internal loss function within Non-negative matrix factorization and run a few experiments.