Techniques for PCA

Pre Requisites

Before learning about the PCA techniques in NLP, let us first learn some basics about NLP itself.

• NLP stands for Natural Language Processing. In NLP, we perform the analysis and synthesis of the input, and the trained NLP model then predicts the necessary output.
• NLP is the backbone of technologies like Artificial Intelligence and Deep Learning.
• In basic terms, we can say that NLP is nothing but the computer program's ability to process and understand the provided human language.
• The NLP process starts by first converting our input text into a series of tokens (called the Doc object) and then performing several operations of the Doc object.
• A typical NLP processing process consists of stages like tokenizer, tagger, lemmatizer, parser, and entity recognizer. In every stage, the input is the Doc object, and the output is the processed Doc.
• Every stage makes some kind of respective change to the Doc object and feeds it to the subsequent stage of the process.

Introduction

Let us suppose that we are working on a large-scale project, for example, calculating the GDP of a country or something like that. Now, for this large-scale project, we will need a lot of data sets. These data sets may itself dependent on the other data sets, and thus it increases a lot of complexity.

Due to the huge data sets, we need to work with a large number of variables. If the number of variables increases, the complexity of management of the relationship among the variables also increases a lot. Since the training of the model largely depends on building the relationship between the dependent and the independent variables, due to a large number of variables, the training of the model also becomes complex in terms of time, computational speed, and space.

A large number of variables not only increases the complexity but also increases the issue of over-fitting. A question may come to our mind - What is this over-fitting? Well, an over-fitting is a situation in which the machine learning model can accurately predict the output for the training data, but it is not able to predict the right output for newer data sets. So, the over-fitting is an undesirable machine learning problem or behavior that we must avoid for better Machine Learning model creation.

The over-fitting may also lead us to violate the assumptions of the modeling tactic that we have used. So, there come picture PCA techniques or Principal Component Analysis techniques that help us to deal with such issues. Let us learn about the PCA techniques in the next section.

What is PCA?

As we have discussed previously that a large number of variables increases the problem of over-fitting. So, we must reduce the dimension of the feature space to tackle this problem. The reduction of the feature space is known as dimensionality reduction in terms of machine learning and natural language processing.

The PCA is one such dimensionality reduction tool that is used to lower the number of variables used in the training. The number of variables is reduced in such a manner that the most crucial information from the original data set is still present. Hence, we use the PCA techniques widely in training huge models.

The dimensionality reduction can be achieved in two different ways, namely- feature elimination and feature extraction. Let us learn about both of these techniques.

1. Feature Elimination

Feature elimination is a pretty simple technique. As the name suggests, feature elimination works by reducing the feature space by directly eliminating the less important features. The feature elimination is quite simple, and it maintains the interpretability of our variables; hence it is a widely used technique.

The feature elimination has some cons as well. As we have dropped some features directly, we will not gain any information from these dropped features. For example, if we want to calculate the GDP of India and earlier we had the data sets of the last 10 years, then the prediction of the next year's GDP is easy. Now, if we have dropped all the previous year's data except the last year's data, then the prediction may or may not be accurate as we have dropped some important features.

So, the elimination of a feature may lead us to eliminate a feature that could have contributed to our model. So, to avoid such an issue, we have another technique called Feature Extraction. Let us learn about this technique.

2. Feature Extraction

Feature extraction is a technique in which we create new independent variables out of the pre-existing independent variables in a specific way. These new independent variables are ordered in such a way that the variable which predicts the dependent variable comes first, and so on.

In this technique, we create the new independent variables, but at the same time, we also discriminate the less important variables with the help of the ordering in which the most important variables come first than the lesser important ones. Now, a question may come to our mind that here also we are discarding the less important features then how is it different from the previous technique? Well, in the feature elimination technique, the newly generated independent variables are made out of the old variables, so even if we are dropping one or more new variables, we still have the impact of old ones.

When to Use PCA?

We should use the PCA techniques in the situations like:

• When the number of variables is too many, and we want to reduce the number of variables, but we are not able to rectify which variable should be removed from our consideration.
• When we want to make sure that the variables are independent of one another.
• When we are comfortable in making our independent variables less interpretable.
• When we want to know the direction in which our data set is dispersed.
• When we want to understand the relative importance of various directions.

How Does PCA Work?

Let us now discuss how the PCA techniques work.

1. To normalize the data.

Before performing the PCA, we standardize the data, which makes sure that each of the features has a mean value of 0 and variance value 1.

2. To build the covariance matrix.

Now after performing the standardization, we start building the covariance matrix, which is nothing but a square matrix that is used to express the correlation between the features of the multi-dimensional data set.

3. To find the Eigenvectors and Eigenvalues.

After making the covariance matrix, we calculate the unit vectors (eigenvectors) and the eigenvalues. The eigenvalues are multiplied with the eigenvectors of the previously calculated covariance matrix.

4. To sort the eigenvectors in highest to lowest order.

Finally, we sort the calculated eigenvectors in the highest to the lowest manner, and then we select the number of the principal components.

Let us take a mathematical example. Suppose we have m dataset, i.e.: x1, x2, …., Xm of dimension n.

Step 1: Then the mean of each feature can be computed using the following equation:

Where,

• $u_j$ : It means of the $j^{\text {th }}$ feature.
• $\mathbf{m}$ : Size of the dataset.
• $\mathbf{x}^{(i)} \mathbf{j}: j^{\text {th }}$ feature of data sample i.

Step 2:

Assuming that we have a dataset of 4 dimensions (a, b, c, d) and the variance is represented as Va, Vb, Vc, Vd for each dimension and Covariance is represented as Ca,b for dimensions across a and b, Cb,c for dimension across b and c and so on.

If we have a dataset X of m*n dimension where m is the number of data points, and n is the number of dimensions, then the covariance matrix sigma is given by:

$\Sigma=\frac{1}{m} \sum_{i=1}^n\left(x^{(i)}\right)\left(x^{(i)}\right)^{\top}$

Step3:

Now we need to decompose the covariance matrix to get the eigenvector and the value. This is done using a single vector decomposition. We can get the eigenvalue and vector using the svd() function. i.e. [U, S, V] = svd()

Where,

• $\boldsymbol{\Sigma}$ : Covariance matrix (sigma).
• U: Matrix containing the eigenvectors.
• S: Diagonal matrix containing the eigenvalues.

$\Sigma=\frac{1}{m} \sum_{i=1}^n\left(x^{(i)}\right)\left(x^{(i)}\right)^{\top}$

Step 4: Now, we can finally sort the eigenvectors in the highest to lowest order.

Extensions to PCA

An extension to the PCA techniques can be the PCR or Principal Component Regression. In the Principal Component Regression, we take the untransformed Y and then regress it on the Z* subset (The z* subset is the feature that we have not dropped).

Refer to the image provided below for more clarity.

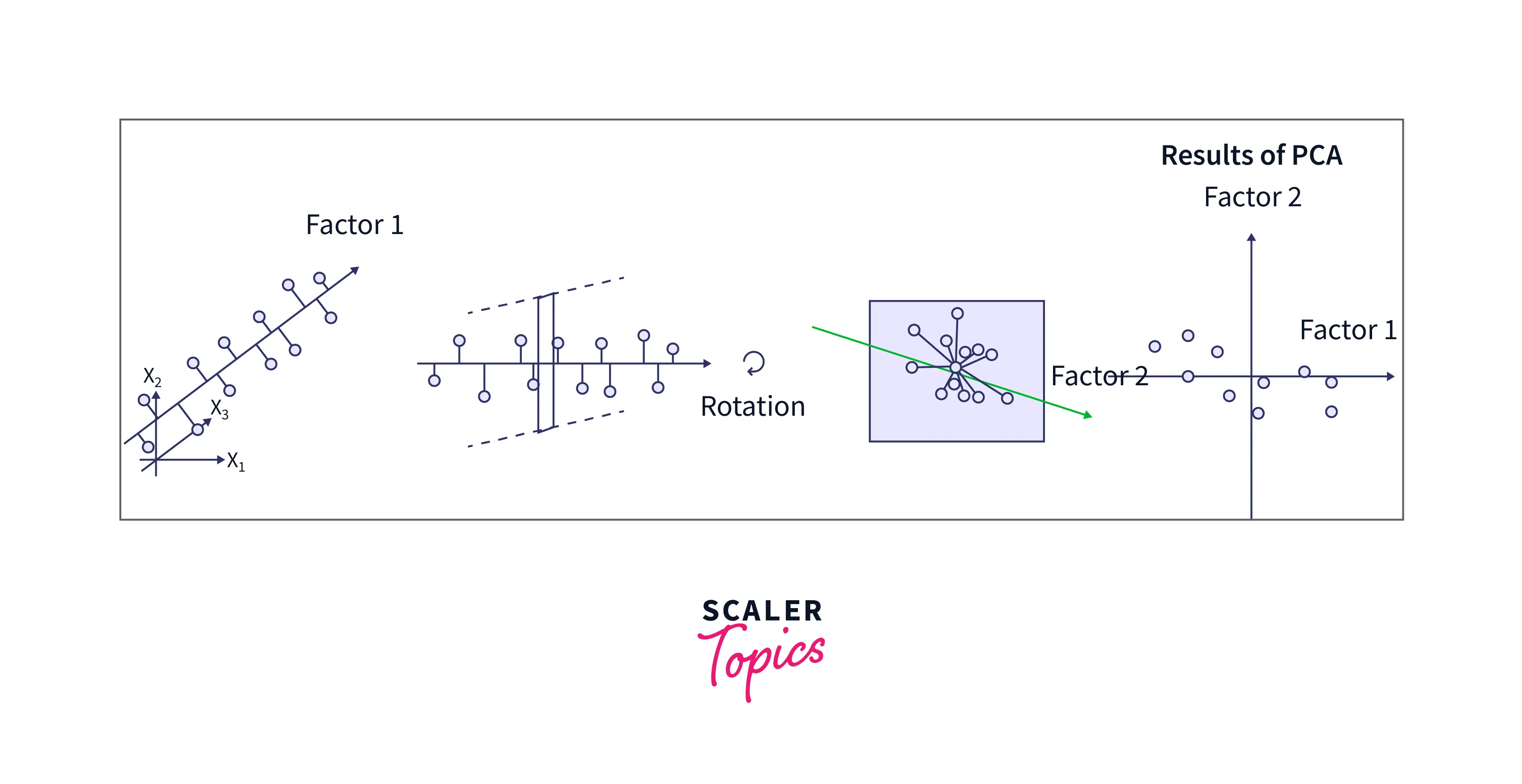
Apart from the Principal Component Regression, the kernel PCA is also a variant of the Principal Component Analysis.