Learning position with Positional Encoding
Overview
This article will first provide a brief overview of positional encoding and how it works. We will then discuss why positional encoding is necessary for NLP tasks and how it can be used to represent the relative positions of words in a sentence. We will provide evidence for the effectiveness of positional encoding and visualize it's working. We will describe how positional encoding is used in the transformer architecture, a popular model for NLP tasks, and provide a tutorial on implementing positional encoding from scratch in Python programming language.
Introduction
Positional encoding has played a significant role in the development of natural language processing(NLP) by providing a way for models to represent the relative or absolute positions of words in a sentence. Before the introduction of positional encoding, many NLP models did not have an inherent understanding of the order or position of words, limiting their ability to accurately understand a sentence's meaning.
With the advent of positional encoding, NLP models could encode additional information about the positions of words in the input, allowing them to differentiate between words with similar meanings but different positions in a sentence. This has significantly improved the performance of NLP models on a wide range of tasks, including language translation, language generation, and text classification.
Example: The judge is always right. Take a right here.
In this example, the word right has two meanings in each sentence depending on the context.
In addition to improving the performance of NLP models, positional encoding has also made it easier to interpret the output of these models. By encoding information about the positions of words in the input, we can use positional encoding to determine the context in which a particular word appears, which can help us to understand why the model made a particular prediction.
What is Positional Encoding
Positional encoding is a technique used in natural language processing (NLP) to represent the `relative or absolute positions of words in a sentence. It is often used in combination with word embeddings, which map words to dense vectors to provide a model with additional information about the order and position of words in a sentence. This is important because many NLP models do not have an inherent understanding of the order or position of words, and thus need this information to be encoded explicitly.
Positional encoding can be implemented in various ways, but a common approach is adding a fixed-length vector to the word embedding of each word in a sentence. This vector encodes information about a word's position in the sentence, allowing the model to differentiate between words with similar meanings but different positions in the sentence.
Positional encoding can be added to the input of a model at the time of training, or it can be incorporated into the model itself as a separate layer. It is usually added to the input of the model to provide the model with additional information about the order and position of words in the input without changing the underlying word embeddings.
Why do We Need Positional Encoding?
Positional encoding is necessary in natural language processing (NLP) tasks because many NLP models do not have an inherent understanding of the order or position of words in a sentence. These models are often designed to process sequences of words, but they do not have a built-in understanding of the relative or absolute positions of the words within the sequence.
For example, consider a simple model that takes a sentence as input and outputs a prediction based on the words in the sentence.
Consider these two sentences A and B:
A: "Even though he did win the best player award, he was , not happy as his team lost." B: "Even though he did not win the best player award, he was happy as his team lost."
Without any additional information about the positions of the words, the model might treat sentence A the same as sentence B. In both cases, the model sees the same set of words, but the meanings of the sentences are completely different because of the order of the words. The position of a single word "not" in this scenario has completely transformed the sentence's meaning.
This is why order matters in NLP. It becomes increasingly important for Transformer based models because they are fed with the whole input embedding, unlike other Seq2Seq models like LSTMs, where the input is fed token by token sequentially.
To address this issue, we can use positional encoding to explicitly encode information about the positions of the words in the input. This allows the model to differentiate between words with similar meanings but different positions in the input and to make more accurate predictions based on the order and position of the words.
In addition to improving the model's performance, positional encoding can also make it easier to interpret the model's output. For example, suppose a model predicts that a particular word is important. In that case, we can use the positional encoding to determine the context in which the word appears, which can help us to understand why the model made that prediction.
Proposed Method
The authors of this paper propose a method of encoding called positional encoding that can be used to provide a neural network model with information about the order of words in a sentence. Positional encoding involves using a $d$ dimensional vector to represent a specific position in a sentence. This vector is not a part of the model itself but is instead added to the input data to provide the model with information about the position of each word in the sentence. This technique is a simple yet effective way of incorporating the order of words into the model, allowing it to understand better the meaning and context of the sentence as a whole. Overall, positional encoding is a clever and effective solution for incorporating the order of words into the input data of a neural network model.
Why not just feed the index of a token $i$ directly to the model? That wouldn't be a good idea because as the sequence length grows, the indices of the latter part of the input also grow. That means we would feed large numbers into the model, a recipe for disaster as it can lead to unstable learning effects like exploding gradients. One way to solve this problem would be to normalize the input indices before feeding into the model so that they stay within a certain range like or .
But that causes another problem, if the input text length varies (as in NLP), the result would contain different positional embeddings for the same positions for different input sequences. This will confuse the model, and the positional embedding might be irrelevant.
There are various ways to implement positional encoding mathematically. Still, one common method involves using a sine and cosine function to create a dimensional vector for each position in the sentence.
If you use a form of the sine function, you will get a graph similar to the one below:
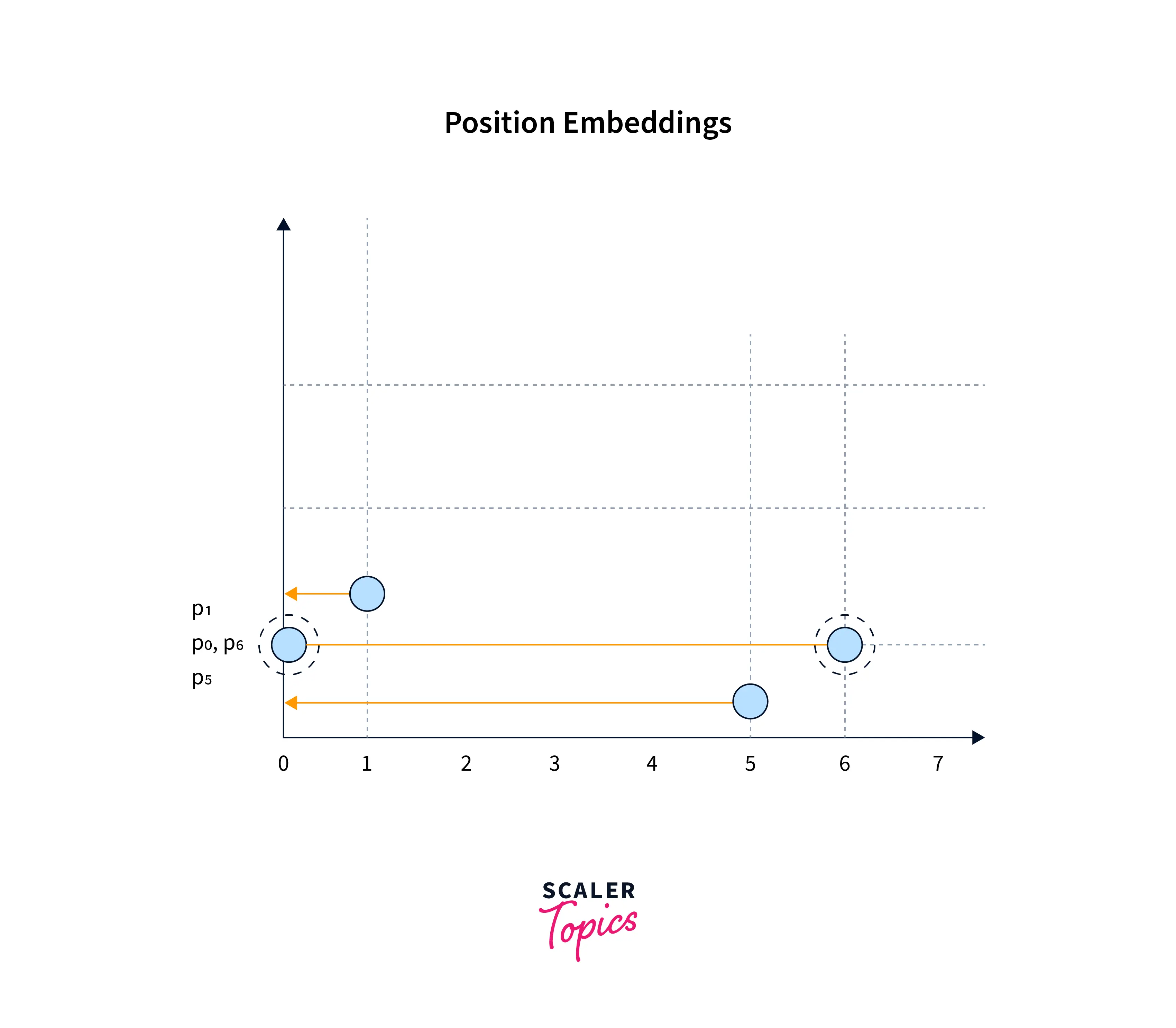
Notice how and are the same in the above graph. This could confuse our model again, as the same positional embedding will be repeated for multiple positions.
To solve this problem, the authors of the original transformer paper used sine and cosine functions of different frequencies and built a matrix. In that way, although the positional embeddings might be the same on lower frequencies, on higher frequencies, they will be different for the same input. This is illustrated in the images below:
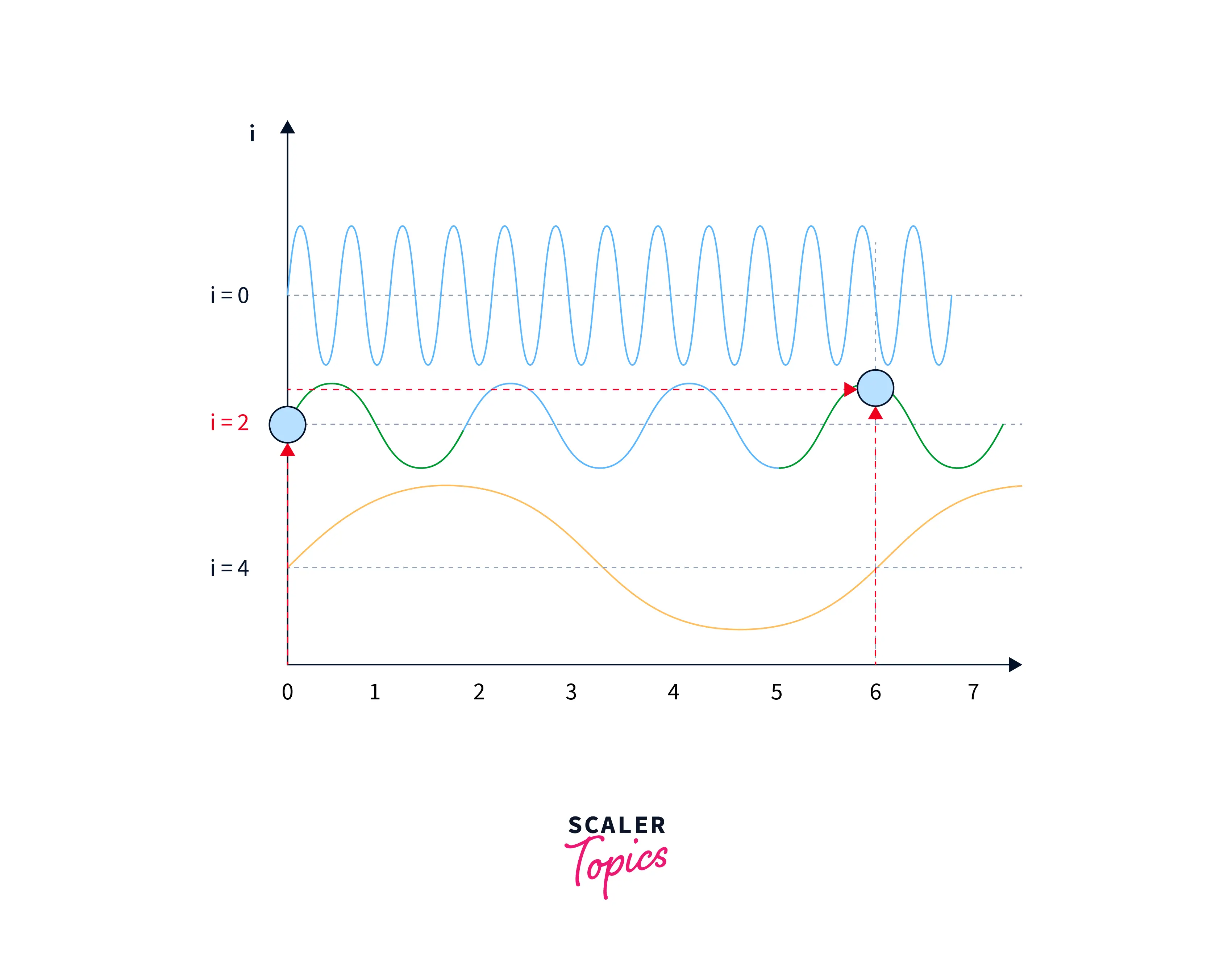
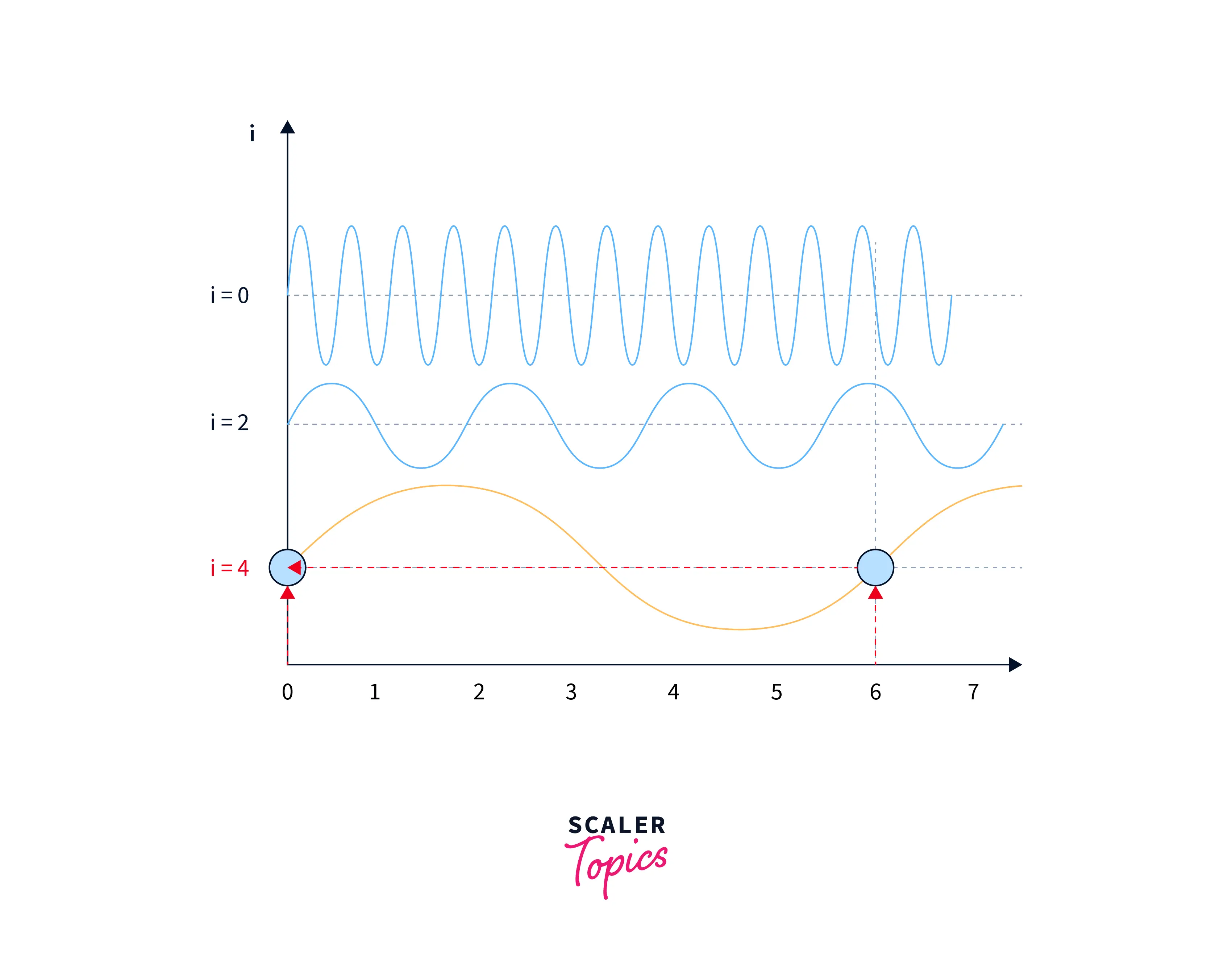
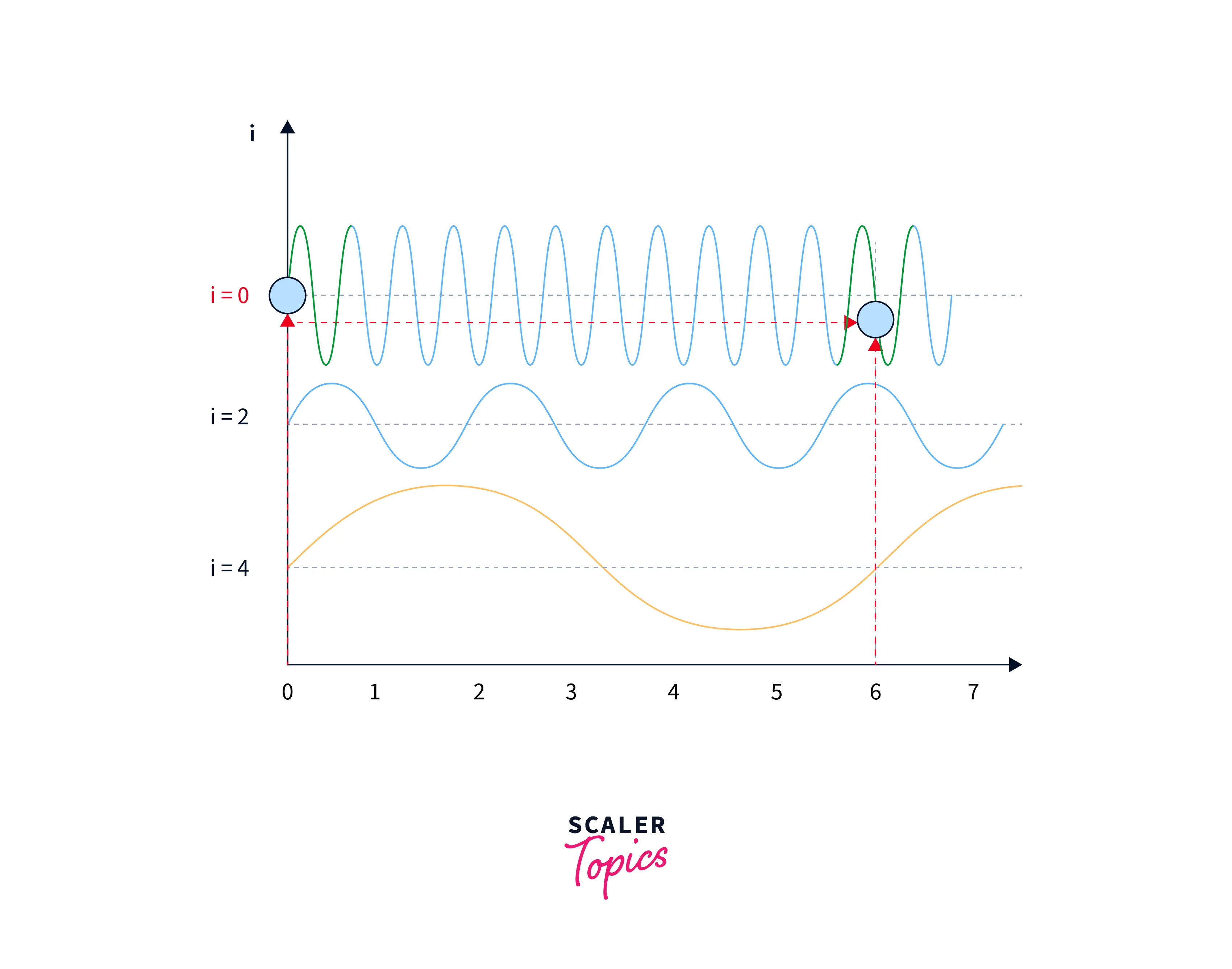
In positional embeddings, both the `sine and cosine functions represent a word's position in a sentence or document. This is because the sine and cosine functions are differentiable and have a smooth, periodic, and continuous nature, which makes them well-suited for representing smooth and continuous variations, such as the position of a word in a sentence or a document.
Using both the sine and cosine functions allows the positional embeddings to capture more information about a word's position in a sentence or document. For example, the sine function can capture the variation of the position over time, while the cosine function can capture the variation of the position concerning the mean or center of the sequence.
Suppose you have a sequence of input data with elements and want to determine the position of the th element within the sequence. In that case, you can use positional encoding to represent this information numerically. Positional encoding involves using sine and cosine functions with varying frequencies to encode the position of each element in the sequence. For example, the positional encoding for the -th element might be represented as:
In the above equation,
- The even positions in the expression are represented by a function, while $cos$ functions represent the odd positions.
- is the position of the word in the input sequence.
- is the dimension of the output embedding
- The user sets to any scalar number, e.g. 10000
- is the index of each dimension in the output vector
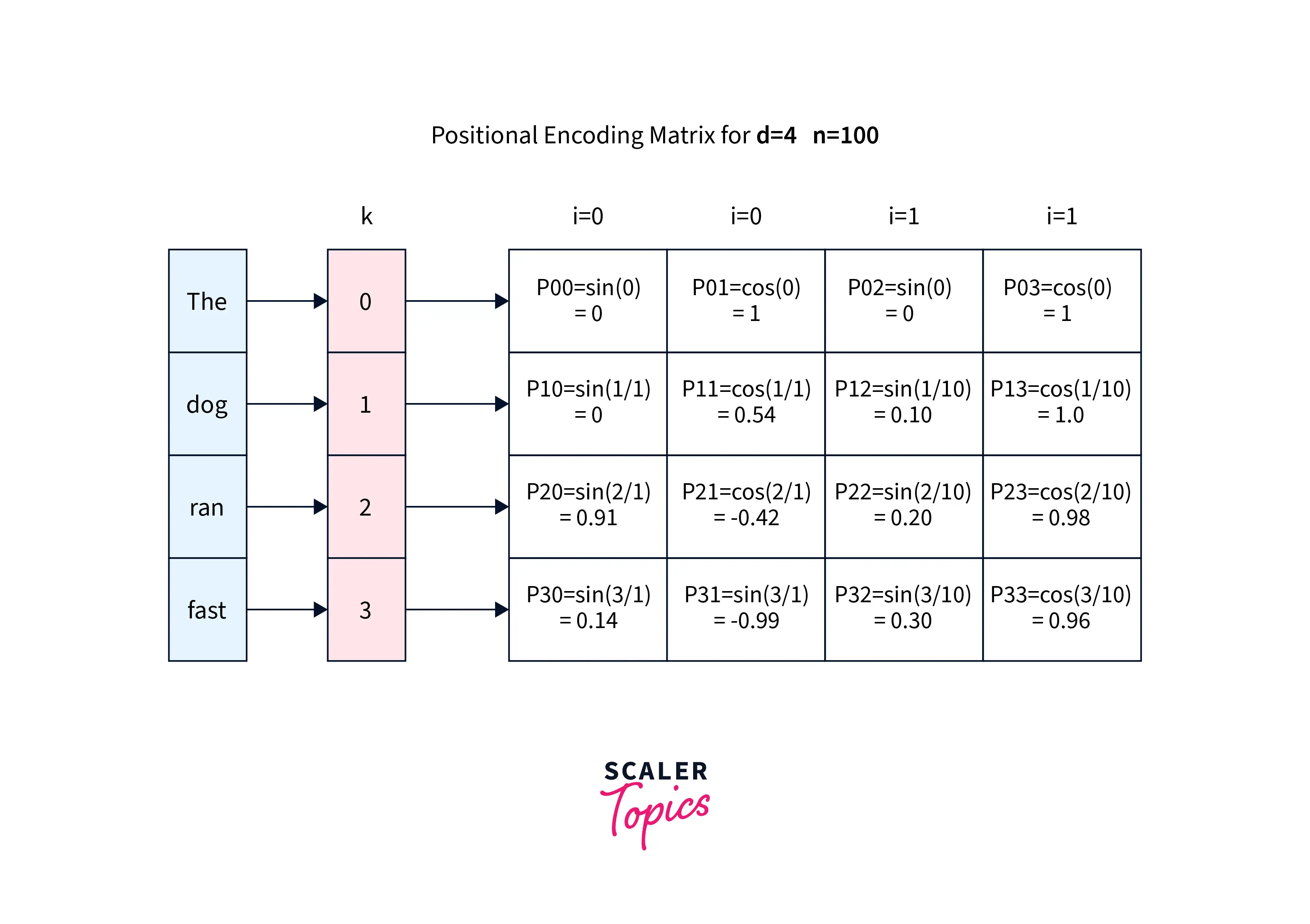
For example,
Let us consider a sentence, "The dog ran fast", with and ; the output positional encoding matrix should be the matrix shown below. It will remain the same for any input with the same length and and .
Relative Positioning
Relative positioning can be achieved in positional encoding by using sinusoidal functions with different frequencies to encode different aspects of the position. For example, we could use one sinusoidal function with a high frequency to encode a word's position within a short sequence window and another sinusoidal function with a low frequency to encode the word's position within a longer window of the sequence.
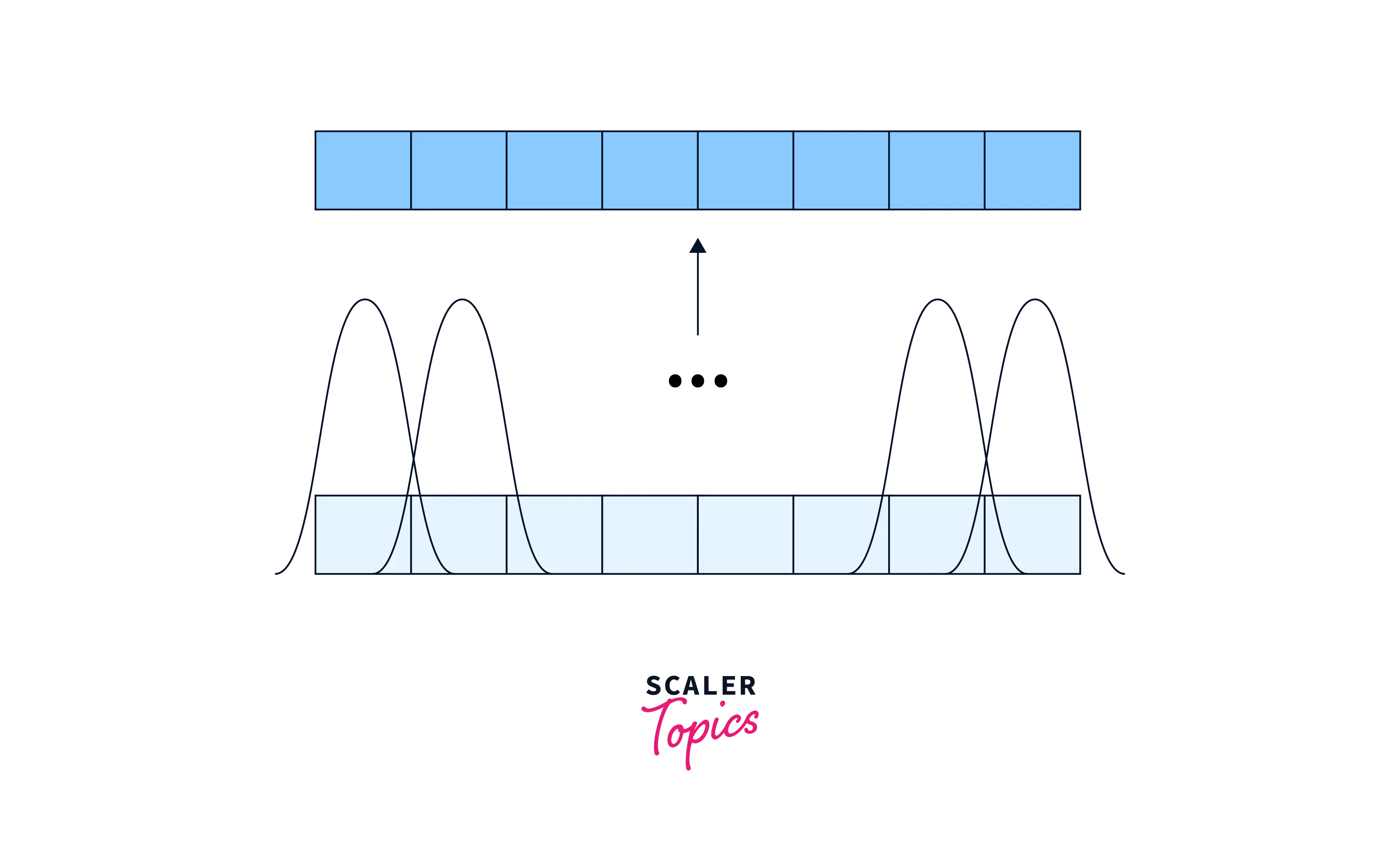
In this way, the model can learn to use the different frequencies of the sinusoidal functions to represent different aspects of the position, such as the position within a sentence, the position within a paragraph, or the position within a document. This can be useful for tasks where the relative position of a word within the sequence is important, as the model can learn to use this information to make predictions.
One way to implement this is to use a multi-headed attention mechanism, where each head is responsible for attending to a different aspect of the position. For example, one head might attend to the position within a sentence, while another head might attend to the position within a paragraph. The model can then learn to use the different heads to attend to different aspects of the position and to weigh them appropriately for the task at hand.
Intuition
Using sinusoidal functions in the positional encoding vector allows the model to incorporate a word's position in the sequence in a way that can be easily learned and used to make predictions. But how?
The use of sinusoidal functions in positional encoding is motivated by the desire to encode a word's position in a sequence in a way that is relatively insensitive to the length of the sequence. If we were to use the position of the word as an encoding, then the encoding for the same position would be different depending on the length of the sequence.
For example, the encoding for the second word in a sequence of length 10 would be different from the encoding for the second word in a sequence of length 100. This could make it difficult for the model to generalize to sequences of different lengths.
On the other hand, if we use sinusoidal functions as the positional encoding, then the encoding for the same position will be approximately the same for sequences of different lengths. This is because the sinusoidal functions have a periodic behavior, so the value of the function at any given position is determined by its angle rather than its absolute position. This means that the encoding for a particular position will be relatively stable across different lengths of the sequence.
In addition to being relatively stable across different sequence lengths, sinusoidal positional encodings have the property that the encoding for a particular position is a function of both the position and the length of the sequence. This can be useful for tasks where the position of a word relative to the length of the sequence is important, as the model can learn to use this information to make predictions.
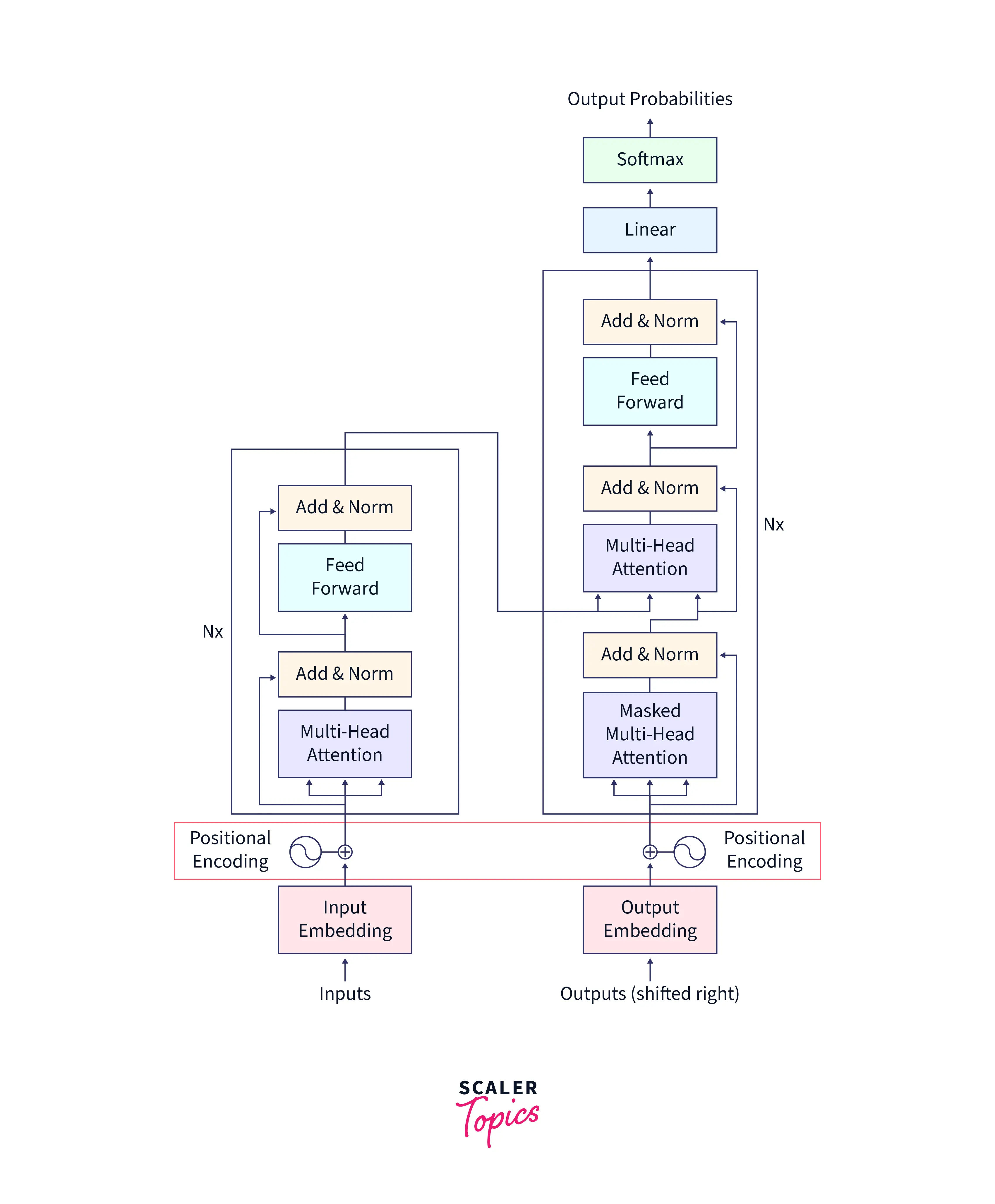
Positional Encoding Layer in Transformers
In Transformers, the Positional Encoding layer is used to add information about the position of elements in the input sequence to the self-attention mechanism. The self-attention mechanism calculates the importance of each element in the sequence for a given prediction but does not take into account the order of the elements. The Positional Encoding layer is added to the input representation to provide information about the position of each element in the sequence, allowing the model to learn the relationship between elements based on both their content and their position in the sequence.
Example
Here's an example of how Positional Encoding can be applied in Transformers for a sentence "I am a student":
Convert each word in the sentence to a vector representation, for example using word embeddings:
Input:
[I, am, a, student]
Embedding:
The word embeddings for the sentence "I am a student" are manually set to
I: [0.2, 0.4, 0.1] am: [0.3, 0.5, 0.2] a: [0.1, 0.3, 0.5] student: [0.4, 0.2, 0.6]]
for demonstration purposes.
Apply the Positional Encoding function to each vector representation based on its position in the sentence:
...and so on for each word in the sentence.
Add the Positional Encoding to the word embeddings to obtain the final input representation:
Final Input:
The final input representation incorporates both the content and position information of each word in the sentence, allowing the Transformer to learn their relationships and make predictions based on this information.
Understanding the Positional Encoding Matrix
The positional encoding function maps each position in the input sequence to a vector by using a sinusoidal function. The wavelength of the sinusoid for a fixed dimension is given by the formula , where is the dimension and is the total number of dimensions. The wavelengths of the sinusoids form a geometric progression and range from to .
 There are several benefits to using this positional encoding scheme:
The sine and cosine functions have values in the range , which keeps the values of the positional encoding matrix within a normalized range.
Each position is encoded using a unique sinusoidal function, allowing for a unique encoding of each position.
The similarity between different positions can be measured or quantified using positional encoding, which enables the relative positions of words to be encoded.
There are several benefits to using this positional encoding scheme:
The sine and cosine functions have values in the range , which keeps the values of the positional encoding matrix within a normalized range.
Each position is encoded using a unique sinusoidal function, allowing for a unique encoding of each position.
The similarity between different positions can be measured or quantified using positional encoding, which enables the relative positions of words to be encoded.
Coding the Positional Encoding Layer From Scratch
Here is an example implementation of positional encoding in numpy.
Positional Encoding Visualization
Values
To calculate the values for each index, we use the given formula. It's worth noting that the value in the cosine function is an even number. Therefore, to calculate the values for the 0th and 1st indexes, we use the following formulas:
This means that the values for the 0th and 1st indexes are only dependent on the value of rather than both and . However, this changes from the 2nd index onward because the dividend is no longer equal to 0, which means that the whole divisor is larger than 1.
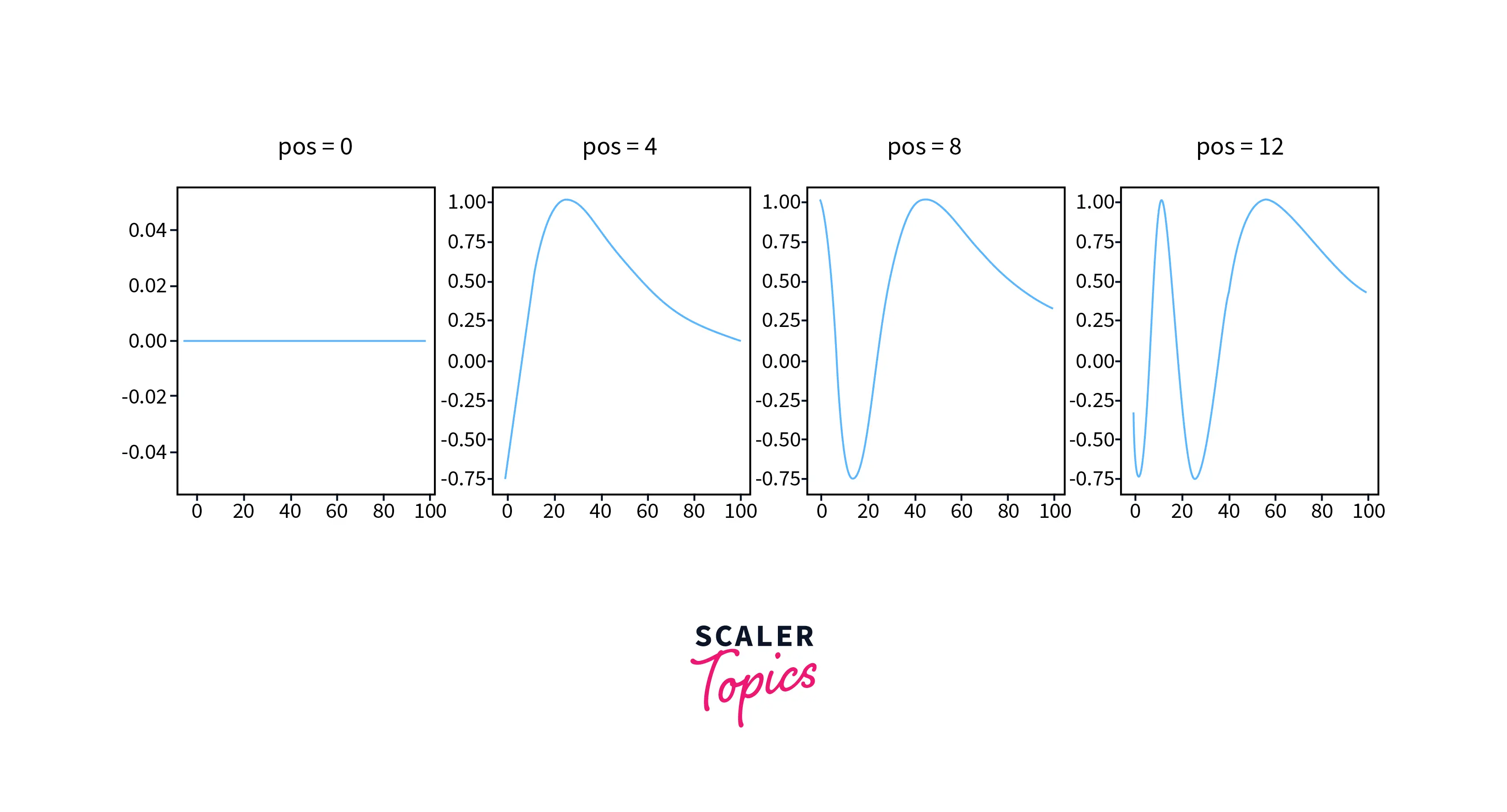
Dimensional Dependency
Now you can compare how the positional embedding (PE) value changes as a function of . The period of the first two indexes changes very little regardless of the value of , but the period of the remaining indexes (starting from the 2nd index) increases as decreases.
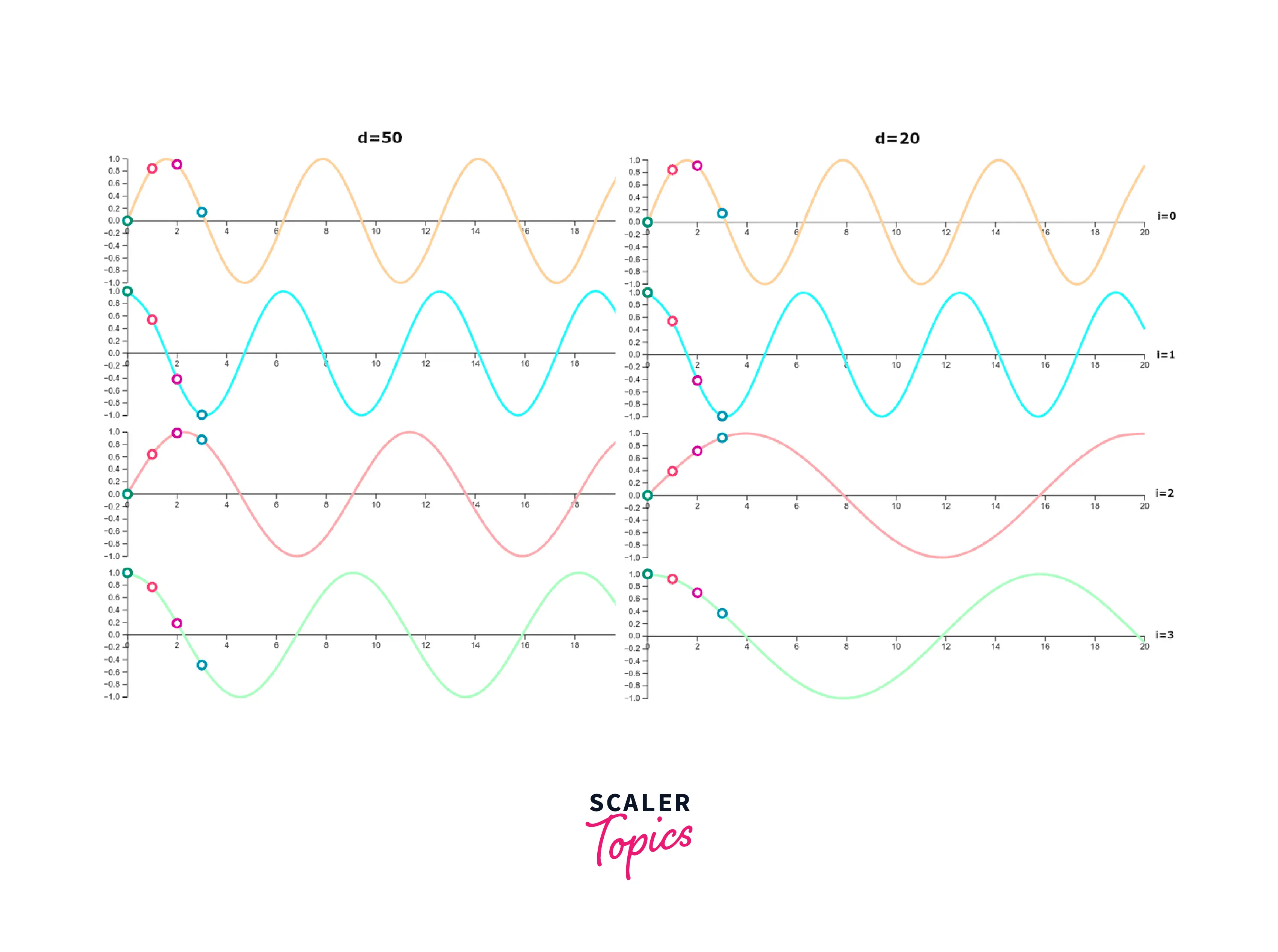
Function Periods
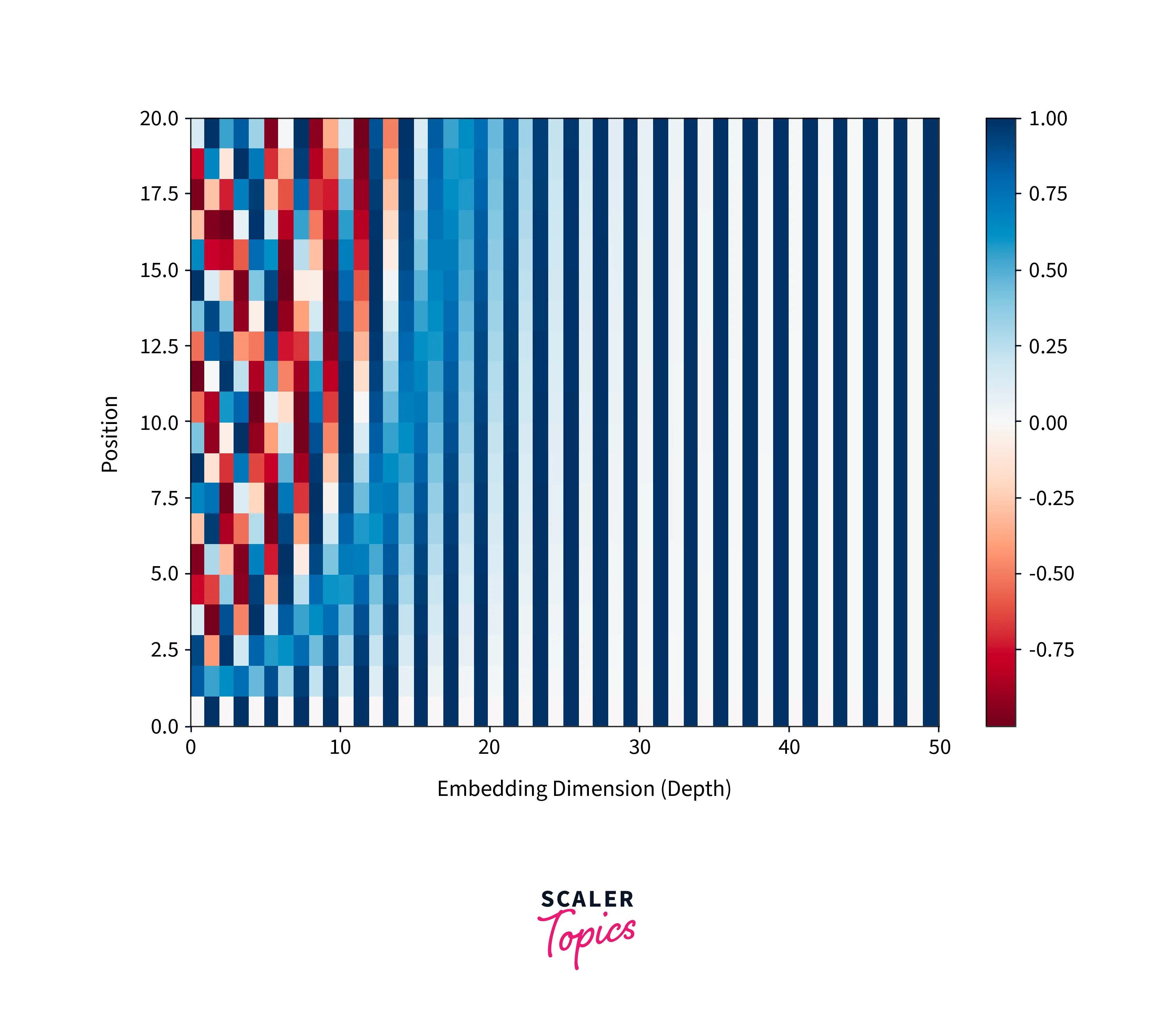
The position vector has shorter wavelengths for lower dimensions. As I increase, the periods of the function also increase. When I reach the value of , a large number of vectors are needed to cover the entire period of the function. The values of the first 20 positions at higher indexes are almost constant. This can be observed in the figure below, where the colors of columns 30-50 hardly change.
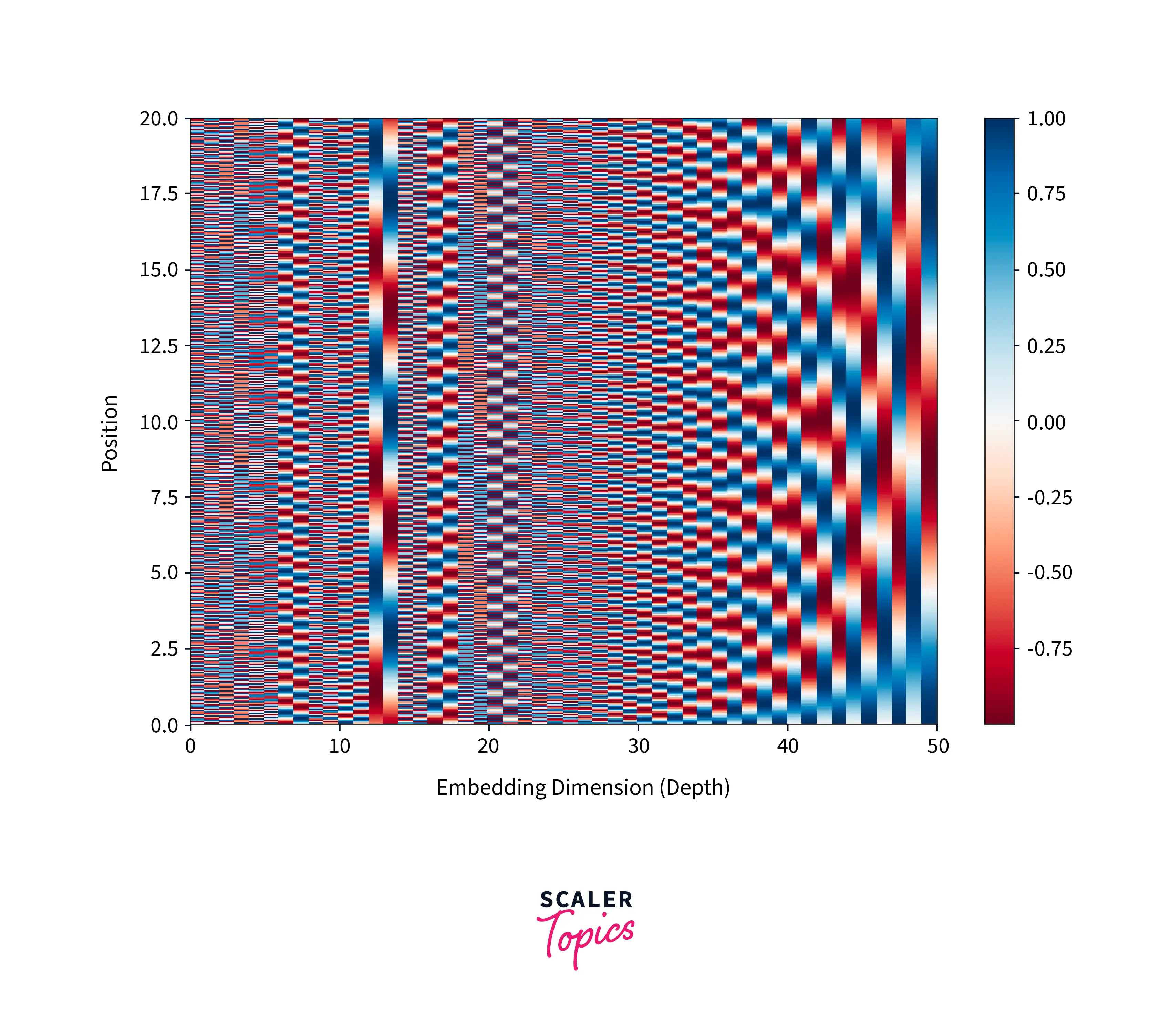
To see significant changes in the values, it is necessary to plot the values for tens of thousands of positions, which is demonstrated in the figure below, where we are plotting for 50,000 positions.
Conclusion
Positional encoding is a method used in natural language processing (NLP) to represent the position of words in a sentence. This is important because the meaning of words can depend on their position in a sentence.
- Positional encoding can be added to the input of a neural network to help it understand the order of words in a sentence.
- One common method of positional encoding is to use sinusoidal functions to create a continuous, periodic representation of the position of each word in the sentence.
- Positional encoding can be combined with other techniques, such as word embedding, to improve the performance of NLP models.
- Positional encoding is often used in transformer models, which are a type of neural network architecture that has been widely used in NLP tasks.
- The use of positional encoding can help NLP models better understand the relationships between words in a sentence, which can improve their ability to understand the meaning and context of the text.
- In general, positional encoding is an important tool for NLP models to represent the meaning and context of text accurately, and it can help improve the performance of these models on various NLP tasks
