Non Linear Data Structure

Overview
A Non Linear Data Structure is one in which its elements are not connected in a linear fashion, as suggested by its name itself. In such a data structure elements might be connected in a hierarchical manner like a tree or graph, or it may be non hierarchical like in a LinkedList.
Non Linear Data Structure have a more complex implementation, than their linear counterparts, but fret not, as we discover more about this topic together!
Takeaways
The main advantage of Non Linear Data Structure is that it uses memory very efficiently than linear data structures.
Introduction to Non Linear Data Structure
Suppose, John and Sarah are two high school students. Their class teacher assigned them to give a detailed list consisting of the names of the Faculties in their year, along with their departments.
John decides to make a table consisting of the names of each person along with his/her department and designations.
| Member Name | Designation |
|---|---|
| Jane | Principal |
| Marilla | HOD, Science Dept |
| Anne | Teacher, Physics |
| Gilbert | Teacher, Chemistry |
| Moody | Teacher, Maths |
| Mathew | HOD, Commerce Dept |
| Jerry | Teacher, Accountancy |
| Prissy | Teacher, Business Studies |
| Mary | Teacher, Economics |
Sarah, on the other hand, decides to make a tree diagram that shows all the faculties along with their designations:
Q. Who do you think will get a better grade in their assessment?
It's Sarah because she has represented the relationship between the faculties while John has only provided a one-sided list that does not show who works under whom. John's list is a linear data structure as you might have guessed, while Sarah's tree is a non linear data structure.
Let us now analyze the key points of a Non Linear Data Structure:
- Elements are not arranged sequentially.
- One element can be connected to multiple elements.
- There might be a hierarchical structure present.
- Here, memory is not allocated in a contiguous manner, unlike linear data structure.
Examples of Non Linear Data Structure
Some examples of non-linear data structures are LinkedLists, Trees, and Graphs. We'll now go through each of them and understand why they are called non linear data structure.
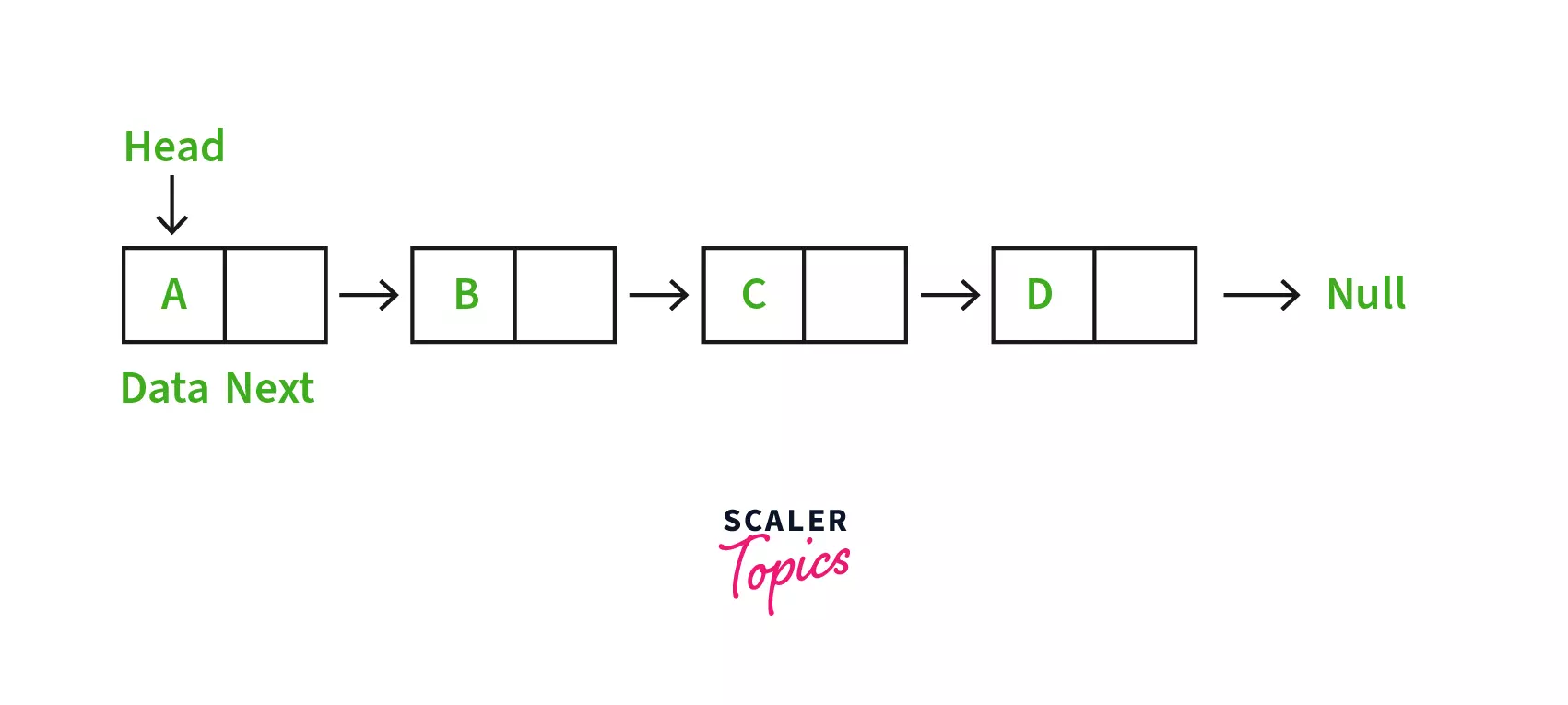
LinkedList
A LinkedList is a collection of nodes. Each node contains a data field, and the address (reference) to the next node.
Q. Why is LinkedList Non Linear?
Even though it might seem that LinkedList should be Linear due to its sequential connection of elements, you must remember that there is no contiguous memory structure in a LinkedList. All the elements of a LinkedList are spread across the memory in a Non Linear fashion, hence it is a Non Linear Data Structure.
Tree
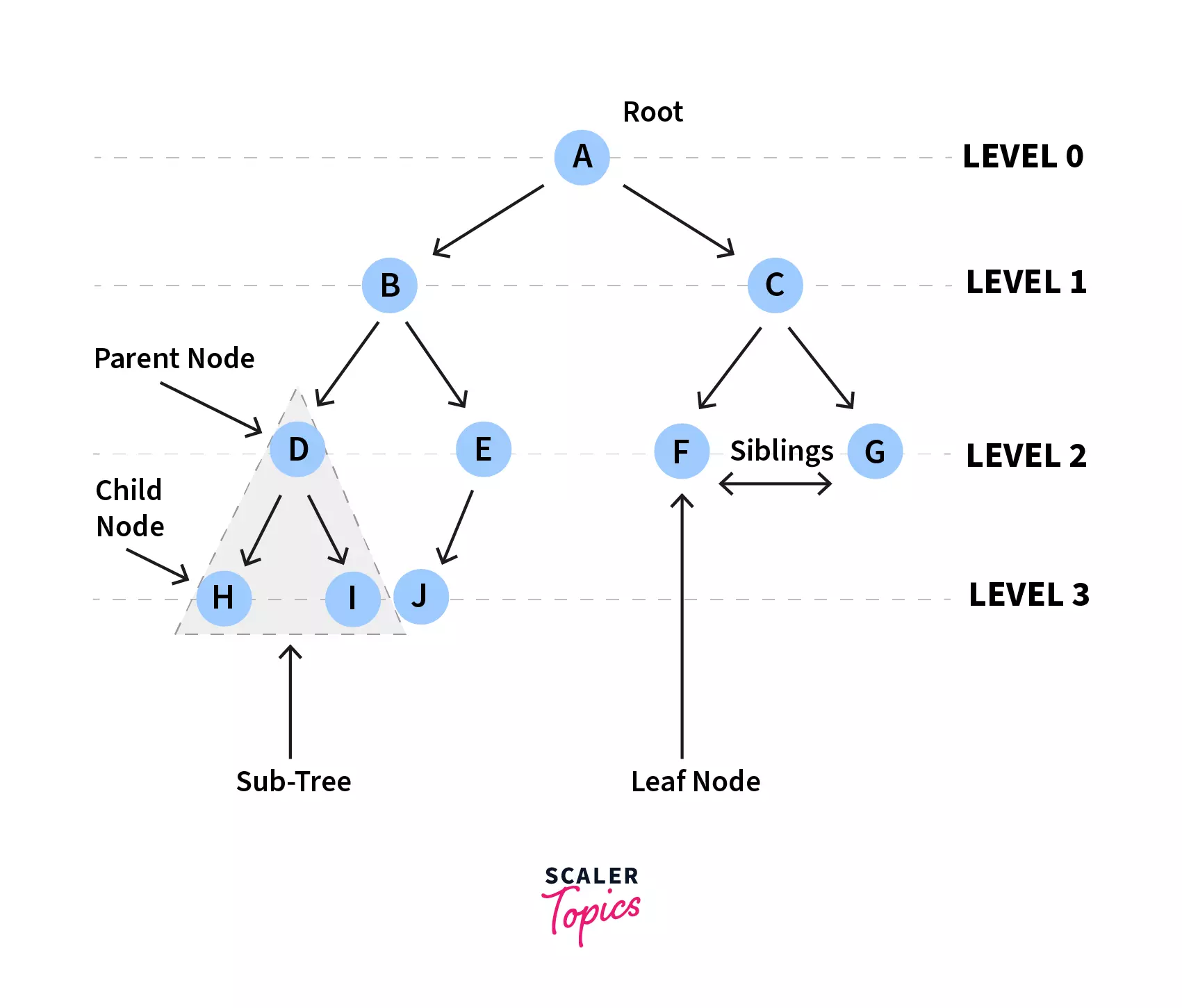
As you might have figured, tree is a data structure that is both non linear as well as hierarchical. Here elements are arranged in multiple levels, and each level can be completely or partially filled. Let us now go through some of the basic terminologies of a tree-
- Root - The topmost node of the tree
- Parent - Each node is a parent of the nodes connected to it, below.
- Child - Each node that is a descendant of another node is called a child of that node.
- Siblings - Nodes with same parent
- Leaf - The nodes in the last/bottom-most level of the tree
- Edge - Link connecting two nodes.
We will now see the types of trees out there:
-
General Tree
A tree that can contain any number of subtrees is known as a general tree.
-
Binary Tree
A tree where each node has at most two children (known as left child and right child) is known as a binary tree. In the figure below, each subtree has either one or two children.
-
Binary Search Tree
Binary Search tree is a special kind of binary tree that holds the following properties:
- All the nodes in the left subtree hold a key with a value lesser than the node's key value.
- All the nodes in the right subtree hold a key with a value greater than the node's key value.
The first figure is a Binary Search Tree since it holds the above two properties.
However, for the second figure, 2 lies in the right subtree of 3 and has a lesser value than 3, whereas, in a Binary Search Tree, all the nodes in the right subtree should hold a key with a value greater than the node's key value. Hence, the second figure is not a Binary Search Tree.
-
AVL Tree
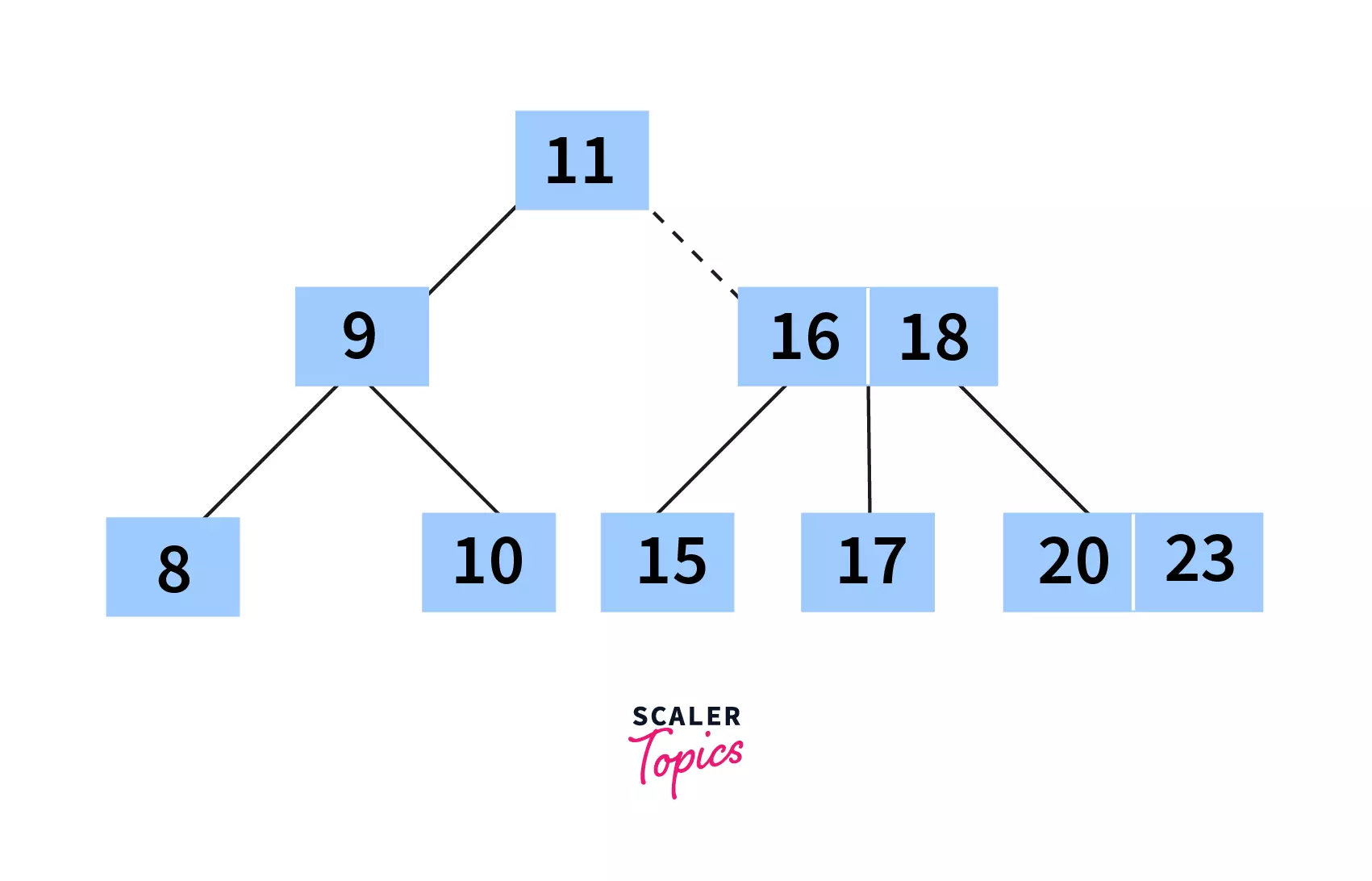
AVL Tree is a special kind of Binary Search Tree where the height difference of the left and right subtrees is less than or equal to one. Eg - In the figure given below, let's analyze height difference of the left and right subtrees for all the subtrees:
| Parent Node of Subtree | Height of left subtree | Height of right subtree | Height difference |
|---|---|---|---|
| 12 | 3 | 2 | 1 |
| 8 | 2 | 1 | 1 |
| 18 | 1 | 0 | 1 |
| 5 | 1 | 0 | 1 |
| 11 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 |
As, we can see, the maximum height difference between any left and right subtree is one. Thus the below tree is an AVL Tree.
2-3 Tree
A tree where every non leaf node has either of the following two properties:
- One data element and two children.
- Two data elements and three children.
Below is a 2-3 tree:
-
B Tree
A B Treehttps://www.scaler.com/topics/data-structures/b-tree-in-data-structure/ helps to store data in sorted order and is commonly used in database or file systems. Below are some of the properties that a B Tree of order m holds:
- There can be at most m children for each node.
- There should be at least ⌈m/2⌉ child nodes for each non-leaf node (except root).
- The root should contain a minimum 1 key.
- Depth of every leaf is the same.
B+ Tree
B+ tree is an extension of B Tree. It often contains a large number of children per node.
Graph
A graph is a non linear data structure that consists of the following:
- Nodes - It is a finite set consisting of vertices.
- Edges - A finite set of ordered pairs in the form of (x,y) that connects any two vertices of the graph.
Let's have a look at the type of Graphs:
-
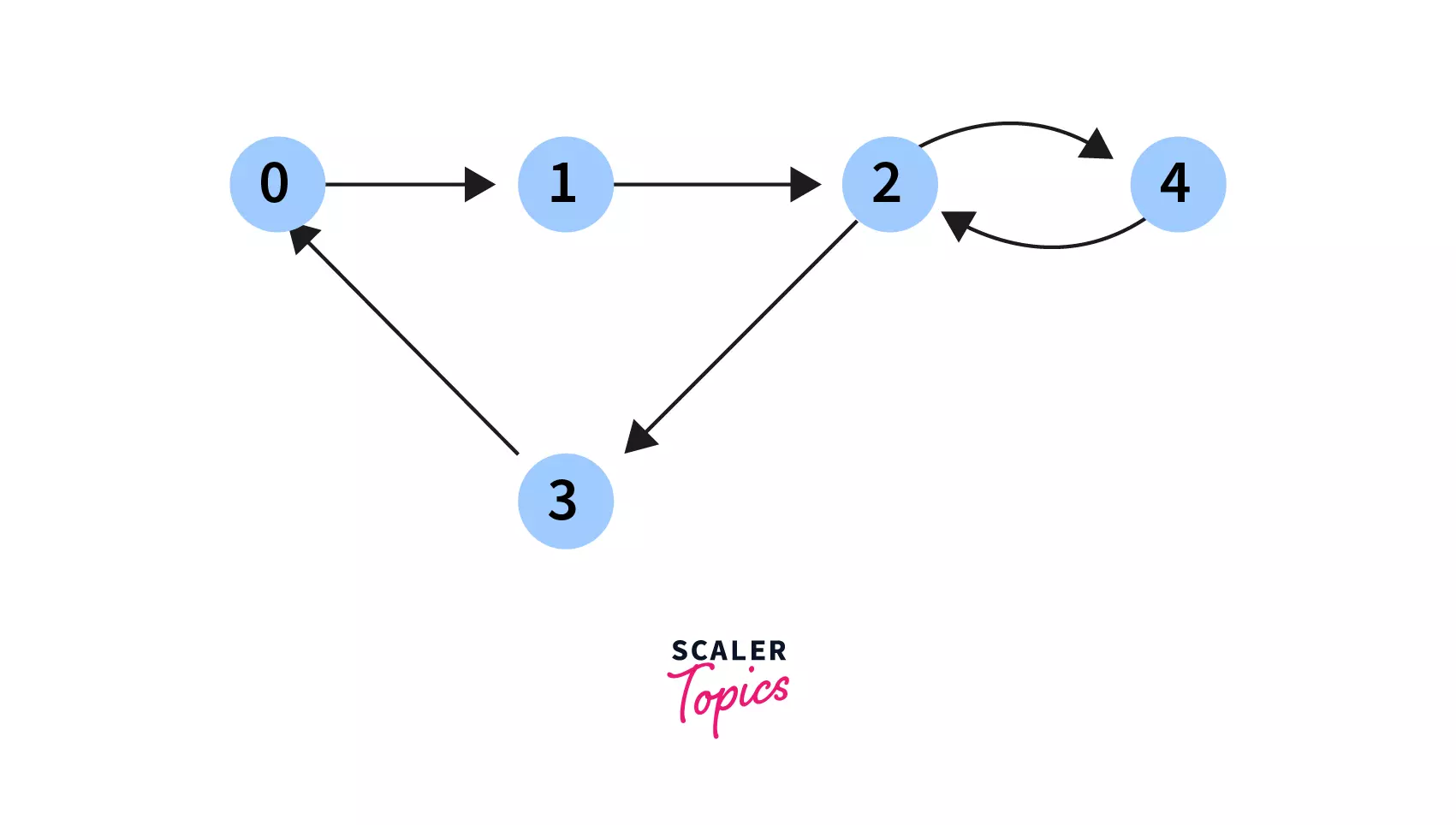
Directed Graph :
As the name suggests, this type of graph contains directed edges, i.e its edges are pointing in a particular direction.
The graph can be traversed only in the direction pointed by the edges.
Undirected Graph :
This type of graph does not contain any direction associated with its nodes, that is its edges are non-directional. We can traverse an undirected graph in either direction.
Q. What is the difference between a directed an undirected edge?
A directed adge points towards a particular direction and is represented by an arrow on the edge. An undirected edge does not point toward any direction and is represented by a straight line.
Weighted Graph :
A graph that has a weight, i.e a certain numeric value associated with its edges is known as a weighted graph. Weighted graphs can be both directed as well as undirected.
These weighted edges can be used to solve a number of problems, such as the minimum cost path to go from one city to another, where the weight of the edges represents the cost to travel between the connected nodes.
Differences between the Linear data structure and Non Linear Data Structure
| Linear Data Structure | Non Linear Data Structure |
|---|---|
| Elements are connected sequentially or in a contiguous manner. | Elements are not connected sequentially or in a contiguous manner. |
| Elements are always present in a single level | Elements may be present in single or multiple levels. |
| There is no hierarchy between the elements. | There is usually a hierarchy between elements. |
| They are easier to implement. | They have a more complex implementation. |
| Memory allocation is sequential. | Memory allocation isn't sequential. |
| Can be traversed in a single run. | Requires multiple runs for traversal. |
| Inefficient utilization of memory. | Memory is utilized efficiently. |
| Examples include arrays, hash tables, stack, queue, etc. | Examples include trees, graphs, etc. |
Code with Confidence! Enroll in Our Online Data Structures Courses and Master Efficient Algorithms.
Conclusion
- Congratulations! Now you have an intuitive idea of what non linear data structures are, and how they differ from the linear data structures out there.
- Feel free to dive deeper into the implementations of the non linear data structures you learned about today, and take up a step up in your Data Structures journey.