Number Pattern Program in Java

Introduction to Number Pattern Program in Java

Number Pattern helps one form different patterns in Java, such as star patterns, character patterns, etc., using conditional loops and syntaxes in Java.

Before moving to Number Pattern Program in Java, let's see how we can understand the pattern.

We can divide the pattern program in Java into two groups, one is the condition of loops and the second is the condition of the print statement.

We can form the conditions of the loops as,

• Observe the number of elements in the rows; if the elements increase, the i loop will start from i=1; otherwise, it will start from i=row or i=x, where x can be any number.
• In each row, observe the order of the elements; if the elements are increasing j loop will start from j=1; else, it will start from j=row or j=i or j=x where x can be any number.

The above trick works on most of the patterns, but we should always cross-verify the conditions of the loop.

And for the condition of the print statement, let's understand it with an example.

Consider the pattern for number n=5,

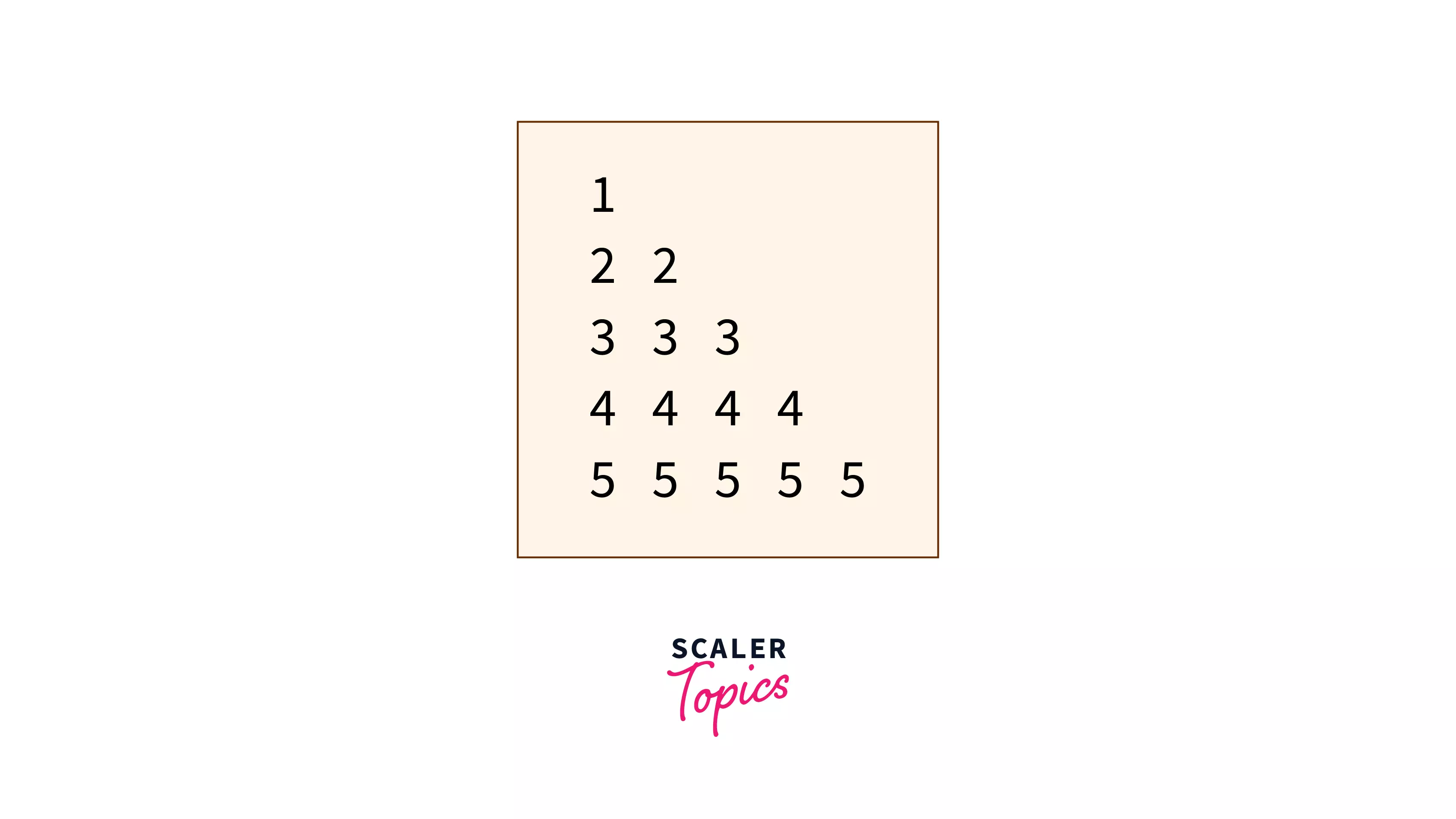
To understand this pattern, convert the pattern into a 2-D Matrix and mention the row numbers and column numbers.

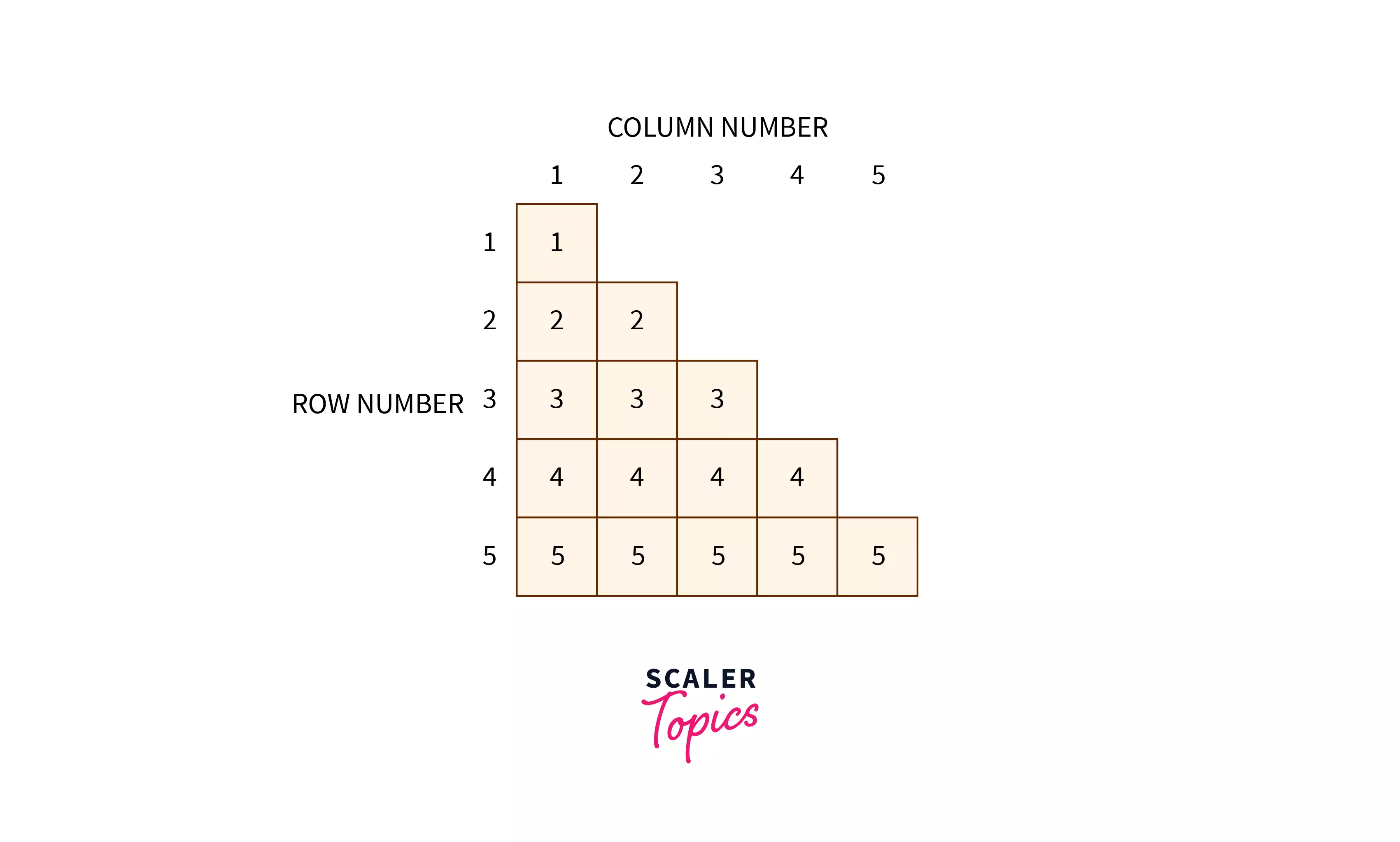
Since the number of elements in the rows is increasing, therefore i loop will start from i = 1 to i = n. In each row there are i elements hence the j loop starts from j = 1 to j = i. But if we look carefully, in each print statement we are printing the row number (By observing the 2-D Matrix). Hence the 2-D matrix helps us to evaluate the condition of the print statement.

Let's code the above program in Java and then we will look at other top number pattern programs in Java.

Output:

In the above program, the number of elements in the rows increases; hence, the i loop runs from i=1 to i=n. j loop is printing each column in the ith row. You can notice here that the j loop runs from j=1 to j=i. Hence the j loop is executing i number of times.

Top Java Number Pattern Program

Pattern Example-1

Pattern

Code

Output:

Explanation

Since the number of elements in each row increases, the i loop is running from i=1 to i=n. In each row, elements are in increasing order; therefore j loop is running from j=1 to j=i. And in each printing operation, we are printing the column number or j.

Pattern Example-2

Pattern

Code:

Output:

Explanation

The above pattern can be divided into 2 triangles.

and,

Upper Triangle is explained in Pattern Example-2. For the Lower Triangle, you can notice that the number of elements in the rows is decreasing; therefore, the i loop is running from i=n-1 to i=1. In each row the elements are in increasing order hence the j loop is running from j=1 to j=i.

Hence, in the first part, we are printing the pattern for n rows and then printing the pattern for n-1 rows in decreasing order from n-1 to 1.

Pattern Example-3

Pattern

Code

Output:

Explanation

As we can observe, the number of elements in the rows decreases. Therefore i loop is running from i=n to i=1. And in each row, the elements are also in decreasing order; therefore, the j loop runs from j=i to j=1.

Pattern Example-4

Pattern

Code

Output:

Explanation The above pattern can be divided into two halves, the upper triangle, and the lower triangle.

and,

In the upper triangle the number of elements in the rows is decreasing therefore, i loop starts from i=n to i=1. In each row, elements are in increasing order therefore j loop is starting from j=1 to j=i.

In the case of the bottom triangle, the number of elements in the rows is increasing therefore, i loop starts from i=2 to i=n. In each row elements, are in increasing order therefore the j loop starts from j=1 to j=i.

Pattern Example-5

Pattern

Code

Output:

Explanation

Since the number of elements in each row increases, the i loop is running from i=1 to i=n. But notice here the ith row contains i elements, therefore j loop is running i times and in each execution of the j loop, we are printing the value of the counter. After printing the value of the counter, we increase the counter value by 1.

Pattern Example-6

Pattern

Code

Output:

Explanation

The number of elements in each row is increasing hence the i loop is running from i=1 to i=n. But notice here the ith row contains i elements, therefore j loop is running i times and in each execution of the j loop, we are printing the value of the counter. After printing the counter value, we increase the counter value by n-j. This formula can be observed by using the 2-D matrix trick explained at the article's beginning.

Pattern Example-7

Pattern

Code

Output:

Explanation

The above pattern can be divided as,

Sub-pattern 1

and

Sub-pattern 2

Adding these two patterns will give us the required pattern. As the number of elements in each row increases, the i loop runs from i=1 to i=n. In subpattern 1, the number of elements in each row increases; hence the j loop starts from j=1 to j=i. In subpattern 2, the number of elements in each row decreases; hence the j loop starts from j=i-1 to j=1.

Pattern Example-8

Pattern

Code

Output:

Explanation The above pattern can be divided into two triangles,

and,

The upper triangle contains n rows; hence the i loop executes n times. Each row contains i-1 spaces, like if i=1, the row contains 0 spaces. If i=2, the row contains 1 space. After the spaces, each row contains elements in increasing order; therefore, the j loop starts from j=i to j=n.

In the lower triangle, there are n-1 rows; hence the i loop is executing n-1 times. Each row contains i-1 spaces. And after spaces, each row contains elements in increasing order; therefore, the j loop starts from j=i to j=n.

Pattern Example-9

Pattern

Code

Output:

Explanation

The above pattern can also be divided into two subpatterns

Sub-Pattern 1

and,

Sub-Pattern 2

Adding these two patterns will give us the required pattern. For sub-pattern 1 the elements in each row are in increasing order; hence the j loop starts from j=i to j=n.

For sub-pattern 2, the elements in each row are in increasing order starting from j=1 to j=i-1.

Pattern Example-10

Pattern

Code

Output:

Explanation

Here the number of elements in each row increases; hence the i loop runs from i=1 to i=n. Also, each row contains i elements, and if the column number is even 0 is printed, else 1 is printed.

More Patterns

Pattern Example-11

Pattern: Hollow Right Angled Triangle (Increasing row wise)

Observation: In this pattern we only want to print the border elements. And we do it with the help of an if statement.

Explanation: We will keep an if, to check if j is 1 or j is i or j is n, and print the value of i, else we will print spaces.

Pattern Example-12

Pattern: Pascal's Triangle

Observation: This pattern is called Pascal's Triangle. Here we start with 1. And the current value is the sum of the nearest 2 values of the previous row.

Explanation: Let's simplify the formula of Pascal's triangle. It is a triangle of binomial coefficients.

For every element in the triangle, we can come up with this formula:

$_iC_j = \frac{i!}{j!(i-j)!}$

We can optimize it by storing the value of the previous iteration. Since, $_iC_j = \frac{i!}{j!\ (i-j)!}$ = $\frac{i!\ (i-j+1)}{j!\ (i-j+1)!}$ = $\frac{i!\ (i-j+1)}{j\ (j-1)!\ (i-j+1)!}$ = $\frac{~i~C~j-1~\ \ *\ \ (i-j+1)}{j}$

Therefore, we will store the previous printed values in a variable.

Pattern Example-13

Pattern: Decreasing Squares

Observation: On first glance, this looks very overwhelming. But we can divide it into smaller patterns.

Explanation: We will try to divide this big pattern into small patterns.

See the image for reference.

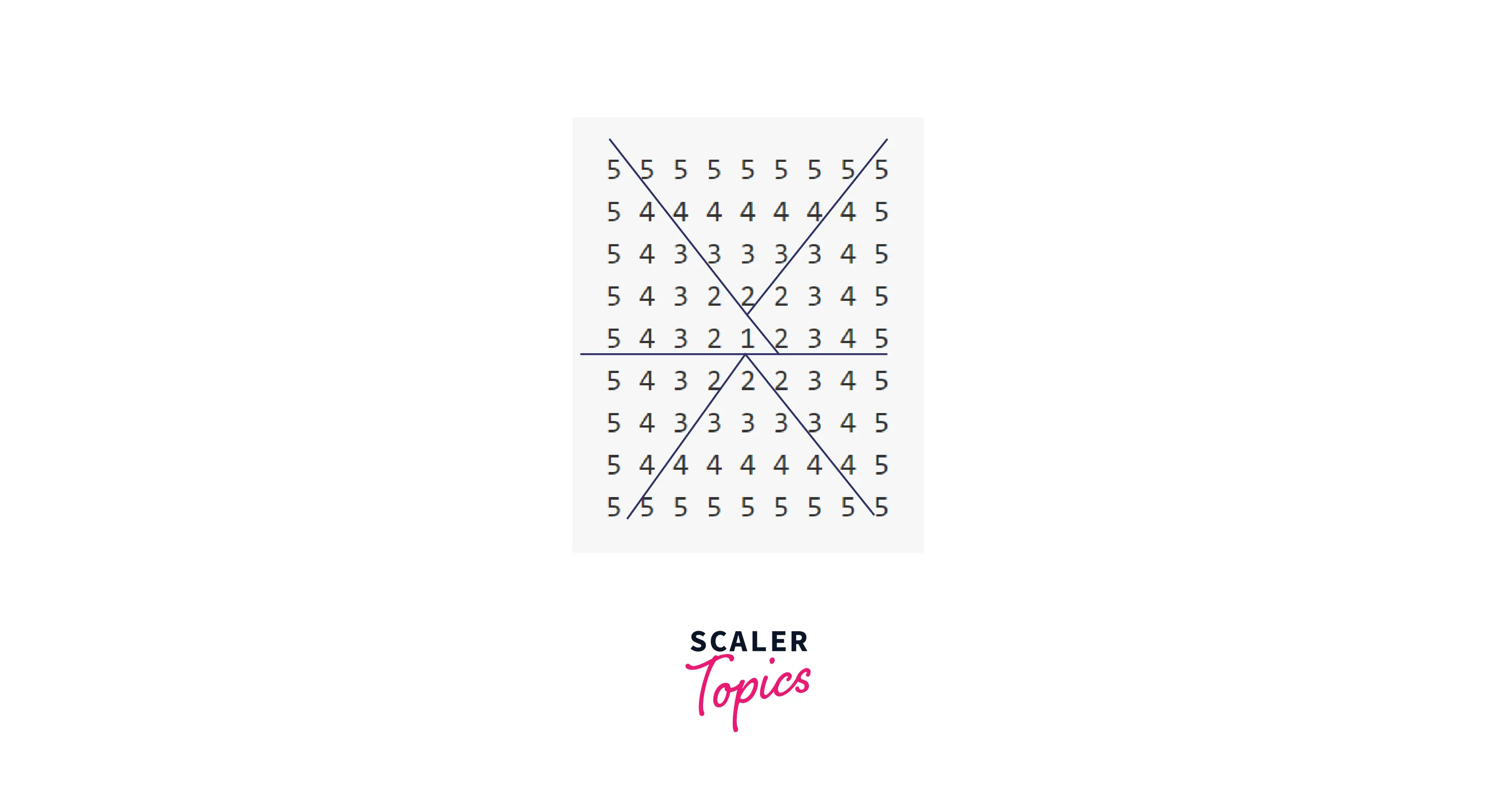
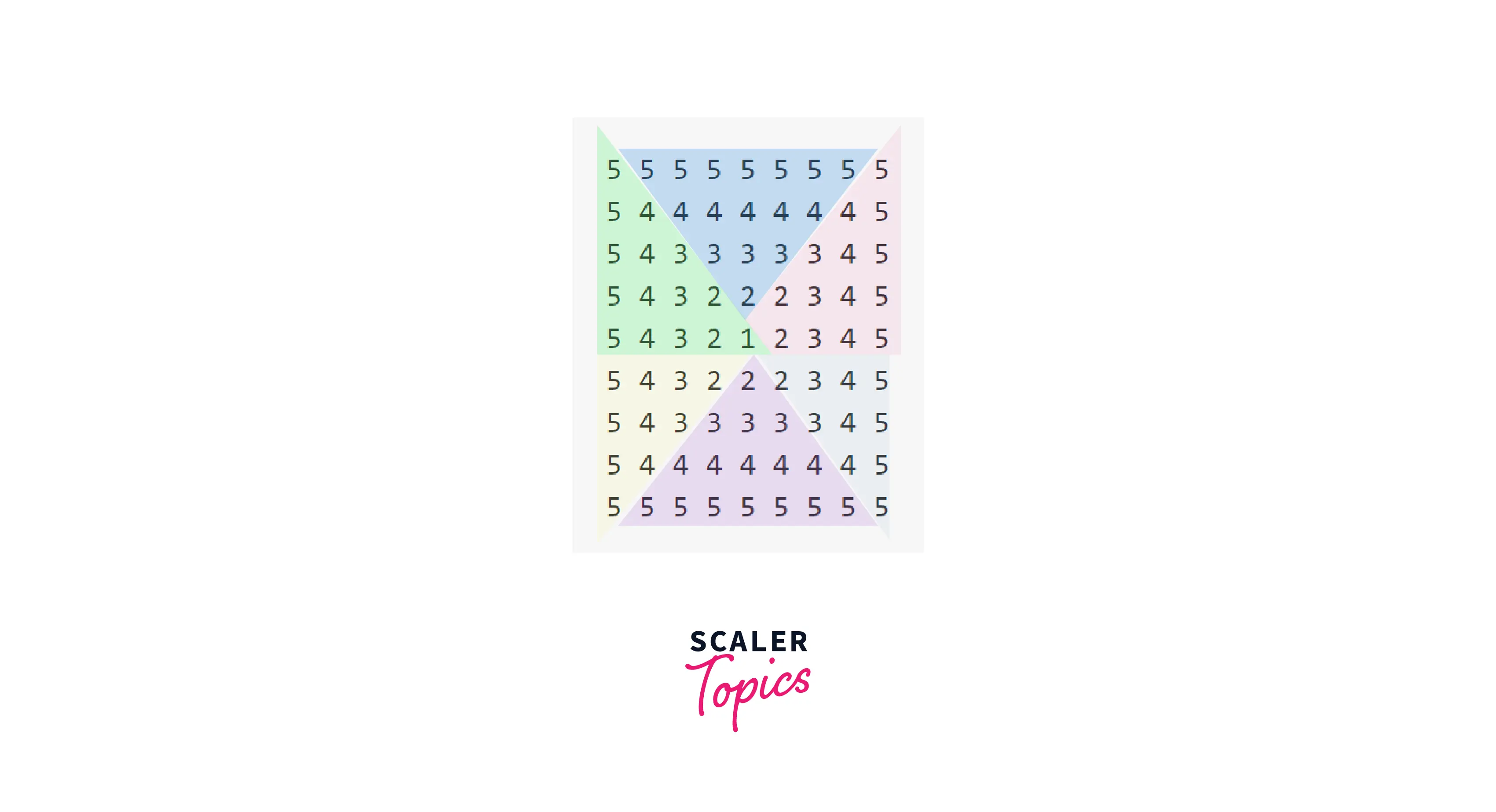
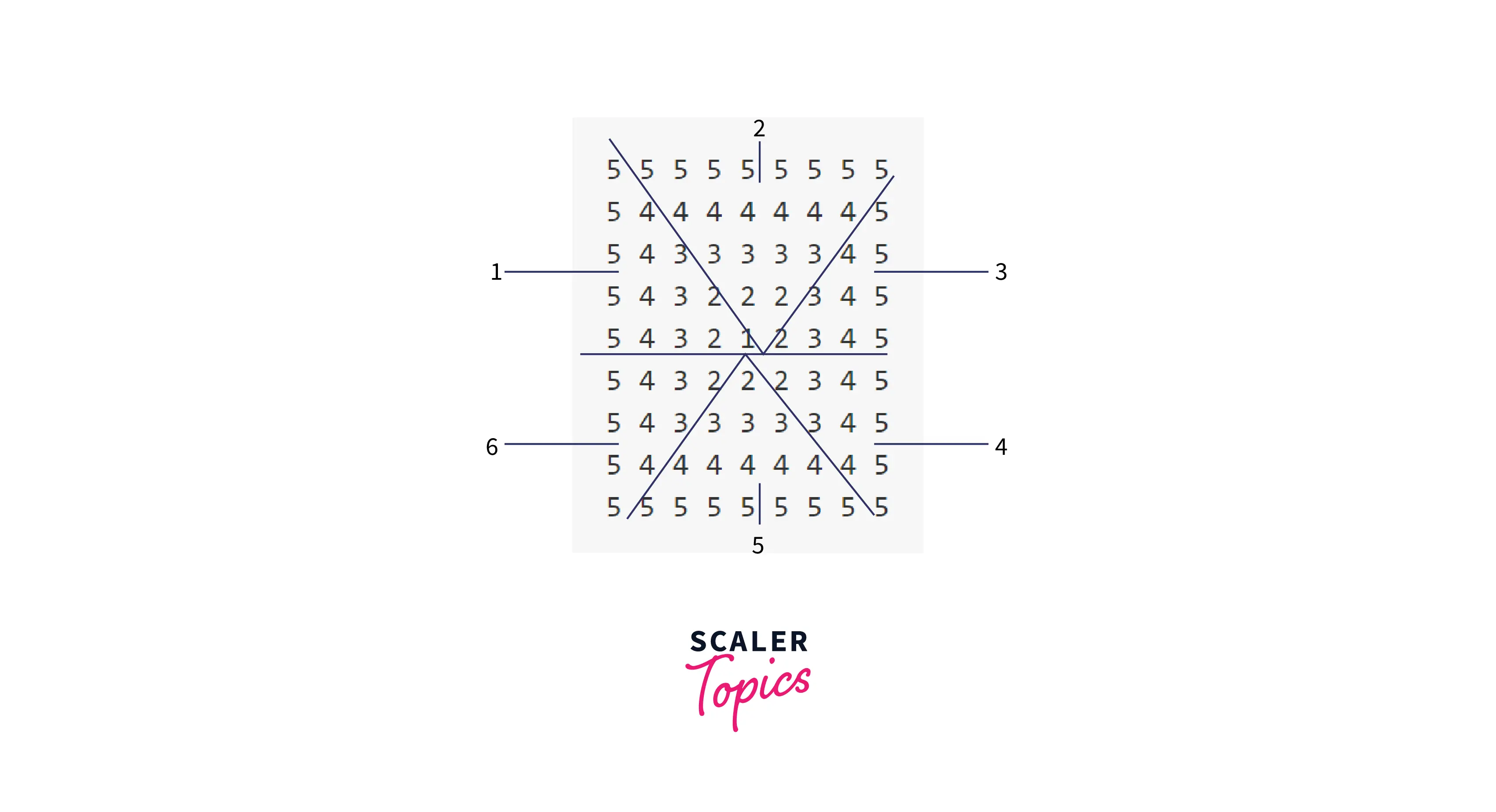
Since we want to print the first 3 triangles, and the last 3 triangles, side by side, we will use 2 pairs nested for loops.