numpy.fft() - How to Apply Fourier Transform in NumPy?

Overview

The Fourier transform is a mathematical function that decomposes a waveform, which is a function of time, into the frequencies that make it up. The result produced by the Fourier transform is a complex-valued function of frequency.

In science and digital signal processing, the Fourier Transform is a practical concept. The original signal's frequency domain representation is provided by the Fourier Transform. In this article, we will go over different ways to apply Fourier Transform in NumPy and its various applications.

Introduction

From audio processing to image compression, the Fourier transform is an effective tool for a lot of analysis, including signal analysis. In NumPy, the SciPy library provides a full-stack implementation of Fourier Transform. We use the NumPy fft() function in SciPy to perform Fourier Transform in NumPy.

Here's the mathematical formula for Fourier Transform :

$\begin{array}{l}F(k)= \int_{-\infty }^{\infty }f(x)e^{2\pi ikx}dx\end{array}$

Furthermore, in this article, we will learn the various uses of the Fourier Transform, its types, and examples.

The Fourier Transform

There are many practical uses of Fourier Transform, like removing unwanted noise from audio, filtering various signals, image reconstruction, and compression. Applications like Shazam use Fourier Transform to get accurate song predictions.

According to their applications, there are different types of Fourier Transform.

Continuous Time Fourier Transform (CTFT)
Continuous Time Fourier Series (CTFS)
Discrete-Time Fourier Transform (DTFT)
Discrete-Time Fourier Series (DTFS)

Here is a quick differentiation between the different types of Fourier Transform :

Transform	Time	Freq	Analysis	Duality
Fourier Transform (CTFT)	C	C	$\begin{array}{l}F(k)= \int_{-\infty }^{\infty }f(x)e^{-2\pi ikx}dx\end{array}$	self-dual
Fourier Series (CTFS)	C, P	D	$\begin{array}{l}\frac{1}{2} a_{o}+ \sum_{ n=1}^{\infty}a_{n}\;cos\frac{n\pi x}{L}+b_{n}\; sin\frac{n\pi x}{L}\end{array}$	dual with DTFT
Discrete Time Fourier Transform (DTFT)	D	C, P	$\mathrm{\mathit{F}\mathrm{\left[\mathit{x}\mathrm{\left(\mathit{n }\right)}\right]}\:\mathrm{=}\:\mathit{X}\mathrm{\left(\mathit{\omega}\right)}\:\mathrm{=}\:\sum_{\mathit{n=-\infty}}^{\infty}\mathit{x}\mathrm{\left(\mathit{n}\right)}\mathit{e^{-\mathit{j\omega n}}}}$	dual with CTFS
Discrete Time Fourier Series (DTFS)	D, P	D, P	$f[n]=\sum_{k=0}^{N-1} c_{k} e^{j \frac{2 \pi}{N} k n} \nonumber$	self-dual

How to Apply Fourier Transform in NumPy?

In NumPy, we can use the NumPy fft() to calculate a one-dimensional Fourier Transform for an array. In NumPy, we use the Fast Fourier Transform (FFT) algorithm to calculate the one-dimensional Discrete Fourier Transform (DFT).

Here's a simple example that should get you started with computing the Fourier Transform of an array using NumPy fft() :

Output :

NumPy fft()

Syntax :

Parameter :
The NumPy fft() function takes in one parameter, which is arr, which represents the input array to which a Fourier series is computed.

Return Type :
The NumPy fft() returns a series of Fourier transformations for the given array.

Examples

Get a Series of Fourier Transform Using Numpy fft() :

In this example, we will create a series of Fourier Transform for an array using the NumPy fft() function provided by NumPy.

Output :

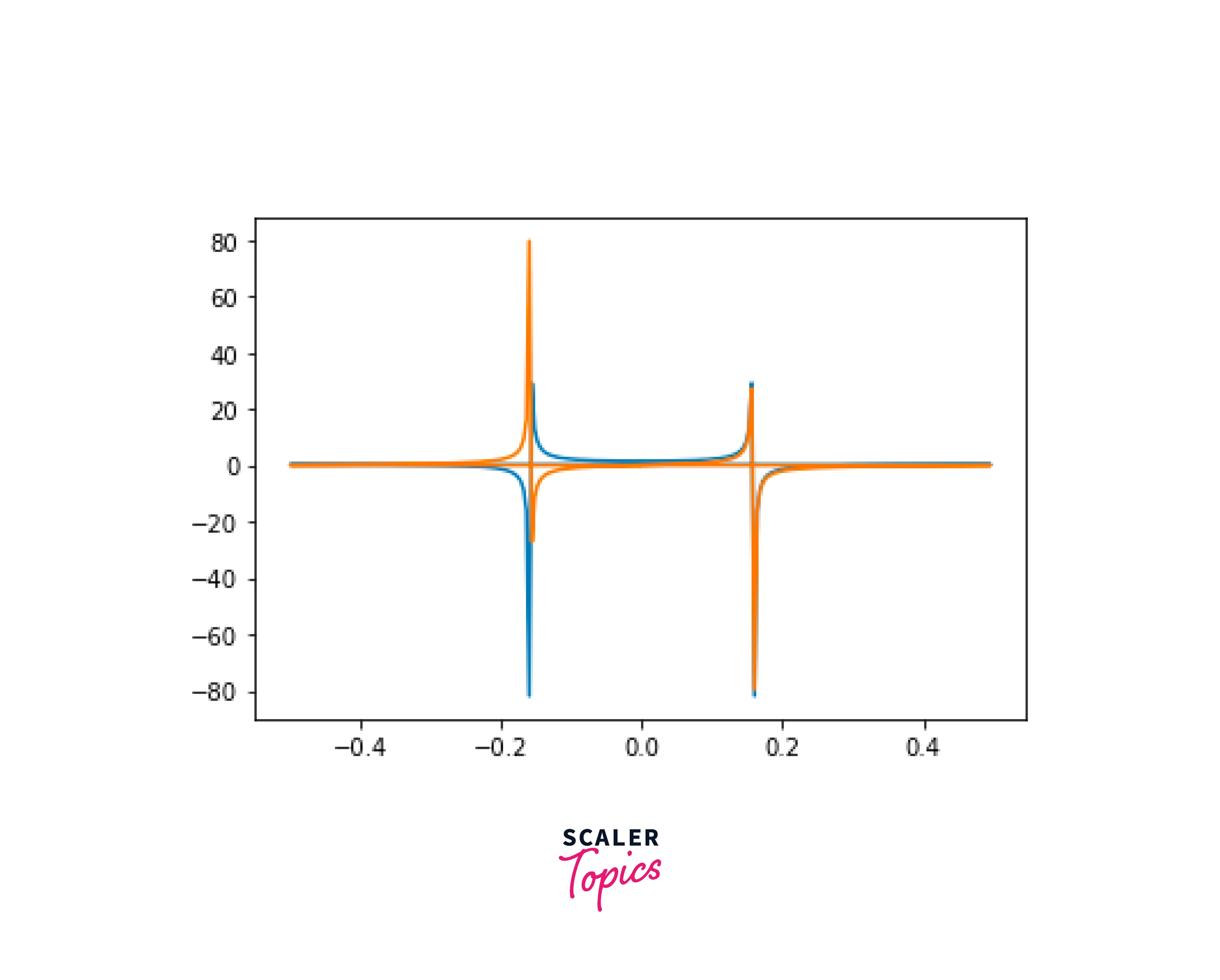
Visualizing the Fourier Transform Using Matplotlib

In this example, we will try to plot our Fourier Series using Matplotlib, which is a visualization library in Python.

Output :

visualizing-the-fourier-transform-using-matplotlib

Conclusion

In this article, we learned about Fourier Transform. A mathematical formula that separates a waveform, which is a function of time, into its fundamental frequencies.
Fourier Transform is instrumental in audio processing, image compression, digital signal processing, and more.
We also covered the different types of Fourier Transforms like CTFT and DTFT (Continuous and Discrete Time Fourier Series respectively).
With the help of some examples, we effectively implemented Fourier Transform using the fft() function provided by NumPy.