How to Implement Different Operations on Matrices in NumPy?

Matrix operations in Python NumPy, play an important role in linear algebra. If you've dabbled with machine learning, you've probably seen matrices in action. But what do we mean by a matrix? A matrix is a two-dimensional or multidimensional grid-like numerical arrangement. Matrix's numbers are grouped into rows and columns. Matrices provide operations like addition, multiplication, and elevating elements to power. Employing matrices enables us to execute linear algebra, which allows us to execute numerous operations on many numbers effectively using matrix operations in Python NumPy.

Before proceeding, it is strongly suggested that you become acquainted with the different NumPy functions. If any of the terms sound unfamiliar, please read the official documentation.

Let's have a look at how we'll generate matrices in NumPy.

Different Operations on Matrices in NumPy

For performing matrix operations in Python NumPy, there are several operations including:

• Addition of matrices
• Subtraction of matrices
• Multiply or divide a matrix by a scalar
• Finding the maximum value in the matrix
• Finding the minimum value in the matrix
• Sum of all values of a Numpy matrix
• Product of two matrices
• Eigenvalues and eigenvectors
• Transpose a matrix
• Trace of a NumPy matrix
• Rank of a NumPy matrix
• Determinant of a square NumPy matrix.
• Inverse a matrix
• Convert a matrix to a list
• Vector norm

Let us go through each of the operations stated above in detail one by one.

Addition of Matrices

The '+' operator is one of the most implemented matrix operations in Python NumPy can be used to execute addition on matrices. Consider the following example to better understand this.

Code:

Output :

Subtraction of Matrices

Subtraction is analogous to addition. We just need to switch from the '+' operator to the '-' operator. Consider the following example to better understand this.

Code:

Output :

Multiply or Divide a Matrix by a Scalar

A matrix's multiplication and division by a scalar is similar to a scalar's multiplication and division by a scalar. For complex computations like Neural Networks and Deep Learning, multiplication, and division by a scalar are considered to be important matrix operations in Python NumPy. Let's consider the following example:

Code:

Output :

How to Create a Matrix of Size m * n using NumPy?

Assume we have a matrix with three rows and three columns, and that's:

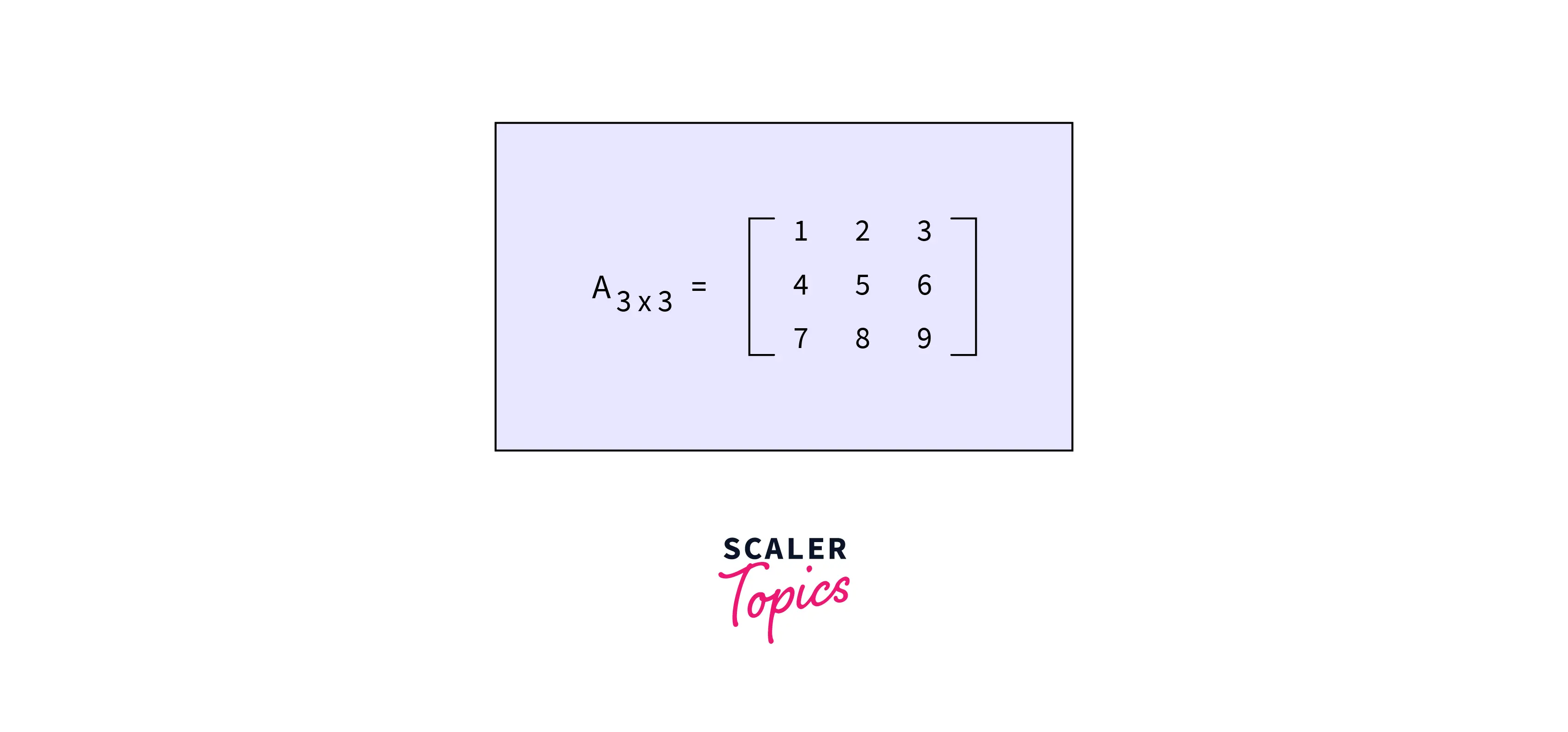
We may use one of the two approaches shown below to generate this matrix in NumPy.

To Construct a Matrix in NumPy, we may use the np.array() function.

In this technique, we will use the np.array() function. First, consider its syntax.

Syntax :

In this function, we supply the Python object to be converted into a matrix ( in our example, a list of lists) as well as the object's data type. It returns the NumPy array on which we will conduct matrix operations.

To generate the aforementioned array in NumPy, use the np.array() method as shown below.

Code:

Output :

To Construct a Matrix in NumPy, We may use the np.matrix() Function

In this scenario, the np.matrix() method is employed. Let us study its syntax.

Syntax :

To transform our data into a NumPy array, we merely supply data and its data type to this method.

Let us now use this approach to produce the aforementioned array for conducting matrix operations in python numpy.

Code:

Output:

Despite the fact that it was effective in producing matrices, it is no longer suggested to use this class, including for linear algebra. Instead, utilize approach 1, which makes use of the np.array() function. It is quite likely that it will be removed from future NumPy versions.

Thus we can observe how the mathematical representation of a matrix is expressed in NumPy in both cases. Each row is surrounded by square brackets, and the entire array is surrounded by a set of brackets.

Now that we know how to construct a matrix in NumPy, let's look at some operations on matrices in NumPy.

Finding Maximum Value in the Matrix

The np.amax() method may be used to obtain the maximum value along a certain axis. Its parameters are an array and an axis along which the greatest value is to be determined. Let's understand this with the help of an example:

Code:

Output:

Finding Minimum Value in the Matrix

It is very similar to the prior operation. The np.amin() function may be used to find the smallest value along a given axis. Its parameters are an array and an axis along which the least value is to be calculated. The amin() and amax() functions are considered to be very important for matrix operations in Python NumPy. Let us attempt to understand this with the assistance of an example:

Code:

Output:

Sum of All Values of a NumPy Matrix

The np.sum() function will be used to determine the sum of all the elements in the NumPy array. This function accepts a ndarray object as input, which represents the original matrix whose elements we wish to sum. It provides a 0-dimensional array or a scalar number that is the sum of all the array items. Consider the following scenario:

Code:

Output:

Product of Two Matrices

When it comes to the product between two matrices, it may be done in two ways: scalar/dot product or cross product. Let us attempt to comprehend each of them thoroughly.

Scalar/Dot Product

The inner product accepts two equal-sized vectors and produces a single integer (scalar). This is computed by multiplying the matching items in each vector and totaling the results. Vectors are one-dimensional NumPy arrays in NumPy.

The number of columns in the first matrix must be equivalent to the number of rows in the second matrix in order to obtain the dot product. We may obtain the inner product either using np.inner() or np.dot(). Both provide the same outcomes. These methods take two vector inputs that must be equal in size. Consider the following illustration:

Code:

Output:

Cross Product

The cross product, also known as the vector product, is a binary operation on two matrices in multidimensions. The result is a matrix that is orthogonal to the matrices being multiplied and perpendicular to the plane comprising them. m x n represents the cross product of two matrices m and n. It is defined as:

$\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \angle(\vec{a}, \vec{b})|\vec{n}|$

where n is a unit vector orthogonal to the plane comprising a and b in the direction provided by the right-hand rule. If one of the matrices being multiplied is zero, or if the matrices are parallel, the cross product is zero. We may obtain the cross product using np.cross(). This method takes two vector inputs that must be equal in size. Let us try to understand this help of an example:

Code:

Output:

How to Get the Eigenvalues of a Matrix?

Assume A is a m x m matrix. If the vector x is non-zero and it satisfies the equation below, then the scalar is said to be an eigenvalue of A.

$Ax = λx$

The vector x is known as the eigenvector of A, and it corresponds to λ.

The np.eig() function in NumPy may calculate both eigenvalues and eigenvectors at the same time. It simply needs the ndarray object as input to calculate the eigenvalues and eigenvectors. Consider the following example:

Code:

Output:

Did you come upon anything interesting? The eigenvalue sum equals the trace of the same matrix! The determinant of a given matrix is equal to the product of the eigenvalues! Don't worry, we'll go over the trace and determinant in further detail later in the text.

If you're familiar with machine learning ideas, you'll know that eigenvalues and eigenvectors are particularly important in Principal Component Analysis (PCA). The principal components (the directions of maximum variance) are represented by the eigenvectors of the correlation or covariance matrix in PCA, and the accompanying eigenvalues reflect the degree of variance described by each principal component.

Transpose a Matrix

A matrix's transposition is determined by swapping its rows and columns. To acquire the transpose, we can use the 'np.transpose()' function, NumPy 'ndarray.transpose()' function, or 'ndarray.T', a specific method that does not need parenthesis. Let us try to grasp this with an example.

Code:

Output:

You must have observed that all of the methods produced the same results.

Trace of a NumPy Matrix

In a square matrix, the trace is the summation of the diagonal elements. We may just employ a ndarray object's trace() function or extract the diagonal components first and then the summation. For example:

Code:

Output:

Rank of a NumPy Matrix

The dimensions of the vector space formed by a matrix's columns or rows are its rank. In other terms, it is the greatest number of linearly independent column vectors or row vectors.

The matrix_rank() function from the NumPy linalg package may be used to determine the rank of a matrix. Consider the following example:

Code:

Output:

Determinant of a Square NumPy Matrix

The determinant of a square matrix may be determined using the NumPy linalg package's det() function. If the determinant is 0, the matrix cannot be inverted. In algebra, this is referred to as a singular matrix. Otherwise, if the determinant is not zero, the square matrix is invertible and is said to be non-singular in algebraic terms. Consider the following example, in which we will examine the determinant of a matrix.

Code:

Output:

How to Inverse a Matrix using Numpy?

As we saw in the last section, a square matrix can be either single or non-singular. Thus, if the matrix is non-singular, we compute its true inverse; otherwise, we compute its pseudo inverse.

True Inverse

The inv() method of the NumPy linalg package may be used to get the true inverse of a square matrix. Consider the following example :

Code:

Output:

We should get an error if we try to calculate the true inverse of a singular matrix. For example:

Code:

Output:

Pseudo Inverse

The pseudo-inverse may be generated even for singular matrices using the numpy linalg package's pinv() function. For example:

Code:

Output:

How to Convert a Matrix to a List?

To transform the array into a list, we may use the NumPy ndarray tolist() method. If the array has more than one dimension, a stacked list is produced. A list containing the array items is returned for a one-dimensional array. The tolist() method takes no arguments. It's a straightforward method for transforming an array into a list format. Consider the following instance:

Code:

Output:

Vector Norm using NumPy

A vector's norm is a measurement of its distance to the origin in vector space. To obtain a vector norm, we employ the Numpy Python library method numpy.linalg.norm(). Consider the following example to better understand it.

Code:

Output:

This brings us to the end of the article. This is only a brief overview of some of the things you can do with matrices in NumPy.