Limitations of Broadcasting in NumPy
Overview
The way NumPy handles arrays with various shapes while performing arithmetic operations is known as broadcasting. The smaller array is "broadcast" across, the larger array, subject to certain restrictions, ensuring that their shapes match. By vectorizing array operations, broadcasting enables Python to be replaced with C for looping. However, there are situations where it is not a good idea to broadcast because it results in inefficient memory usage that slows computation.
Introduction
The concept of broadcasting in NumPy is quite helpful. When using arrays for arithmetic operations, the array size is a crucial idea. Arrays can never have the same shape. The way NumPy handles arrays with various shapes while performing arithmetic operations is known as broadcasting. The smaller array is "broadcast" across, the larger array, subject to certain restrictions, ensuring that their forms match. By vectorizing array operations, broadcasting enables Python to be replaced with C for looping. It accomplishes this without duplicating data pointlessly and typically results in effective algorithm implementations. However, there are situations where it is not a good idea to broadcast because it results in inefficient memory usage that slows computation.
Limitations of Broadcasting
Although as good of a thing broadcasting is, there are some cases where it is not advised to use broadcasting, or attempting broadcasting on non-broadcastable NumPy arrays leads to an error.
Let's look at an example.
Output:
Now let's try changing the shapes a bit.
Output:
This resulted in an error because the dimensions of the two arrays were not compatible with the multiplication operation as per mathematical rules on matrices and arrays. We can also observe the error given by NumPY states the arrays could not be broadcasted together with their respective shapes. In simple words, a 4x1 array and a 3x1 array could not be multiplied together.
Let's look at a case where NumPy broadcasts the arrays.
Multiplication by a Scalar
Output:
Here the two arrays were of different shapes, yet how could they be multiplied together?
Let's see how NumPy made this possible.
Here the array a was a 1x3 array and we can call b a 1x1 array.
Internally NumPy stretched the array b into a 1x3 array with the same element all over the array.
This would be more clear with an illustration.
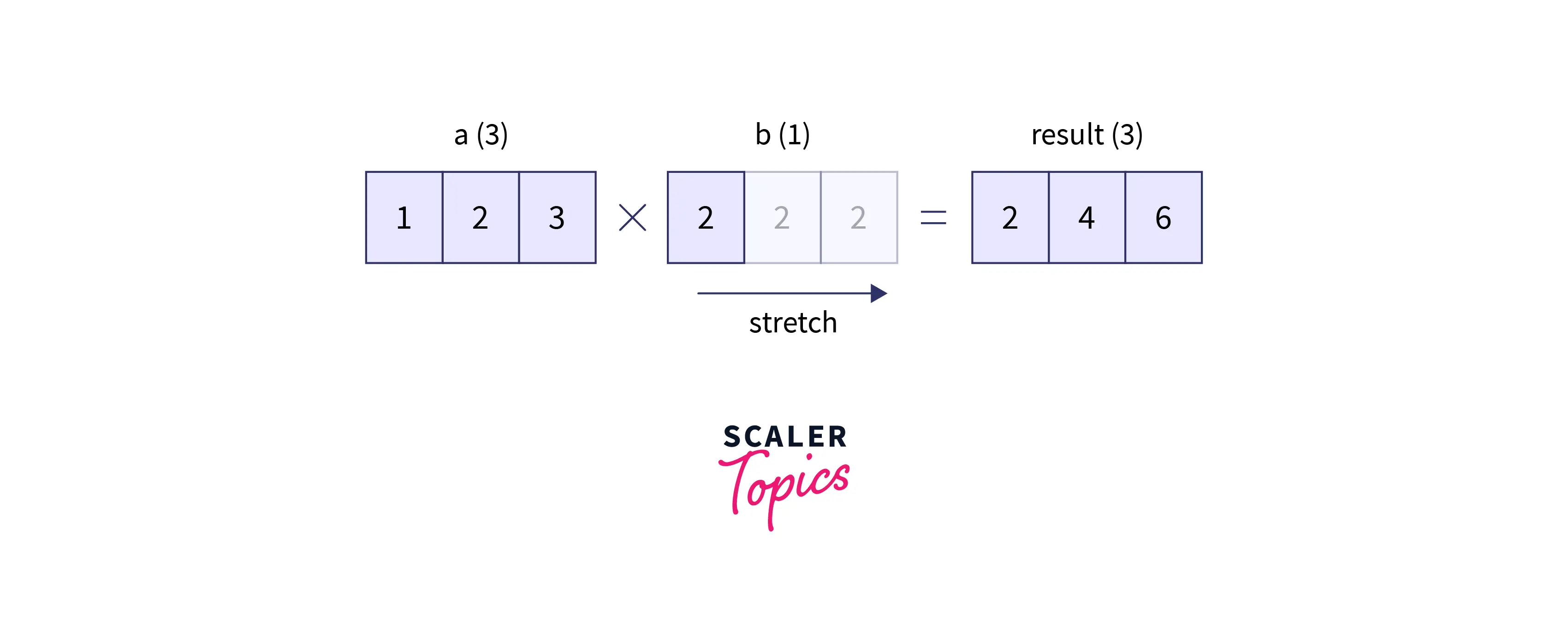
This same principle is applied to different cases in broadcasting.
Let's look at some of the different cases of broadcastable arrays.
Note: ? (Question mark) the below table stands as a variable that can take any number, in which broadcasting can be possible.
| Dimensions of First Array | Dimensions of Second Array | Dimensions of Resultant Array |
|---|---|---|
| 5x4 | ?x1 | 5x4 |
| 5x4 | ?x4 | 5x4 |
| 15x3x5 | 15x1x5 | 15x3x5 |
| 15x3x5 | ?x3x5 | 15x3x5 |
| 15x3x5 | ?x3x1 | 15x3x5 |
When using Numpy arrays, the broadcasting tool is incredibly simple and useful. Nevertheless, numerous guidelines and limitations must be followed.
Keep in mind that the ndim attribute and the shape attribute can both be used to determine the ndarray's number of dimensions and form, respectively.
The dimensions and geometry of the arrays are limited. Broadcasting is possible when both arrays have the same shape or only if one has a size of 1. Additionally, we must take the dimensions into account for the reverse. We count it from the trailing dimension.
Violation of deviation from any of these rules will result in an error in broadcasting. Hence we can term these rules as limitations of broadcastable arrays.
Different Cases that are not Broadcastable
Now we have seen some different cases of broadcastable arrays, let's look at some cases where it's not broadcastable.
Output:
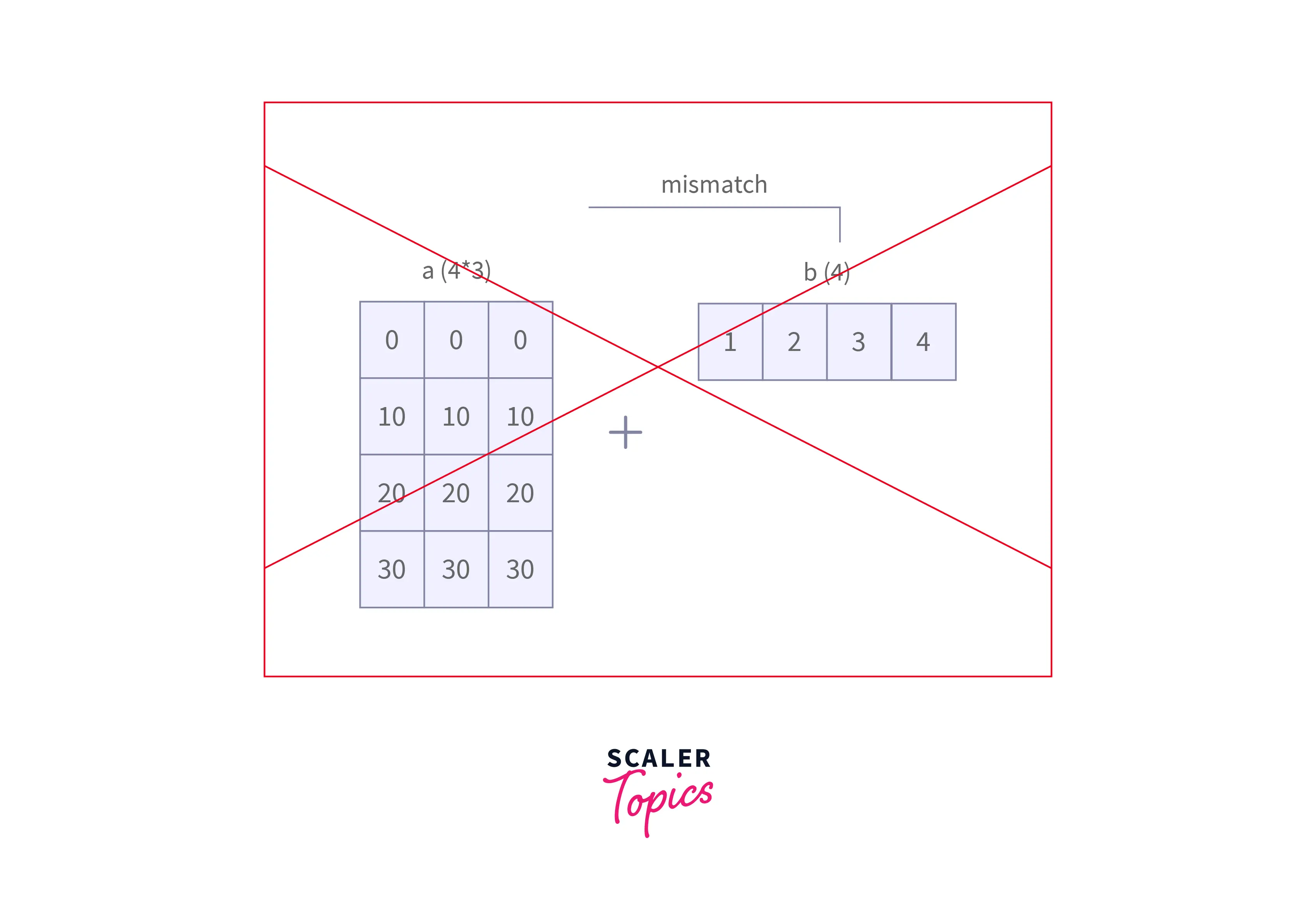
Explanation: A dimension can only be stretched if the initial size is 1. It cannot be broadcasted, and an error is raised if the dimensions have different sizes and none of the arrays' sizes is 1.
Let's look at another case.
Output:
Examples
Let's look at some examples of broadcastable and non-broadcastable arrays.
- Broadcastable Arrays
It is similar to the case of operation by a scalar value on an array, as mentioned before.
- Broadcasting in 1-D array
Output:
- Broadcasting in 2-D array
Output:
- Non-Broadcastable Arrays
Output:
Conclusion
Let’s look at what we have learned here.
- NumPy handles arrays with various shapes while performing arithmetic operations with something known as broadcasting.
- Broadcasting is possible when both the arrays have the same shape or only if one has a size of 1.
- Some examples of both broadcastable and non-broadcastable arrays.
