Matrix Library with NumPy
Overview
There are multiple techniques for storing data in the wide realm of Computer Science. If we want to store our data in a contiguous way, we use Arrays; if we want to store key-value pairs, we use a HashMap; if we want a hierarchical way of storing data, we might use a Linked-List, and so on.
This article will focus on one of the most commonly used data-structure, a matrix.
Introduction
A NumPy matrix is essentially a table with rows and columns of numbers. The size of the NumPy matrix is determined by the number of rows and columns it has, similar to how arrays are created in programming.
For instance, consider the following 4x4 matrix, which has four rows and four columns:
A 3x4 matrix, on the other hand, with three rows and four columns, looks like this:
Matrices are so identical to arrays that in certain computer applications, arrays are utilized to represent matrices. In a program, the 3x4 matrix could be represented as follows:
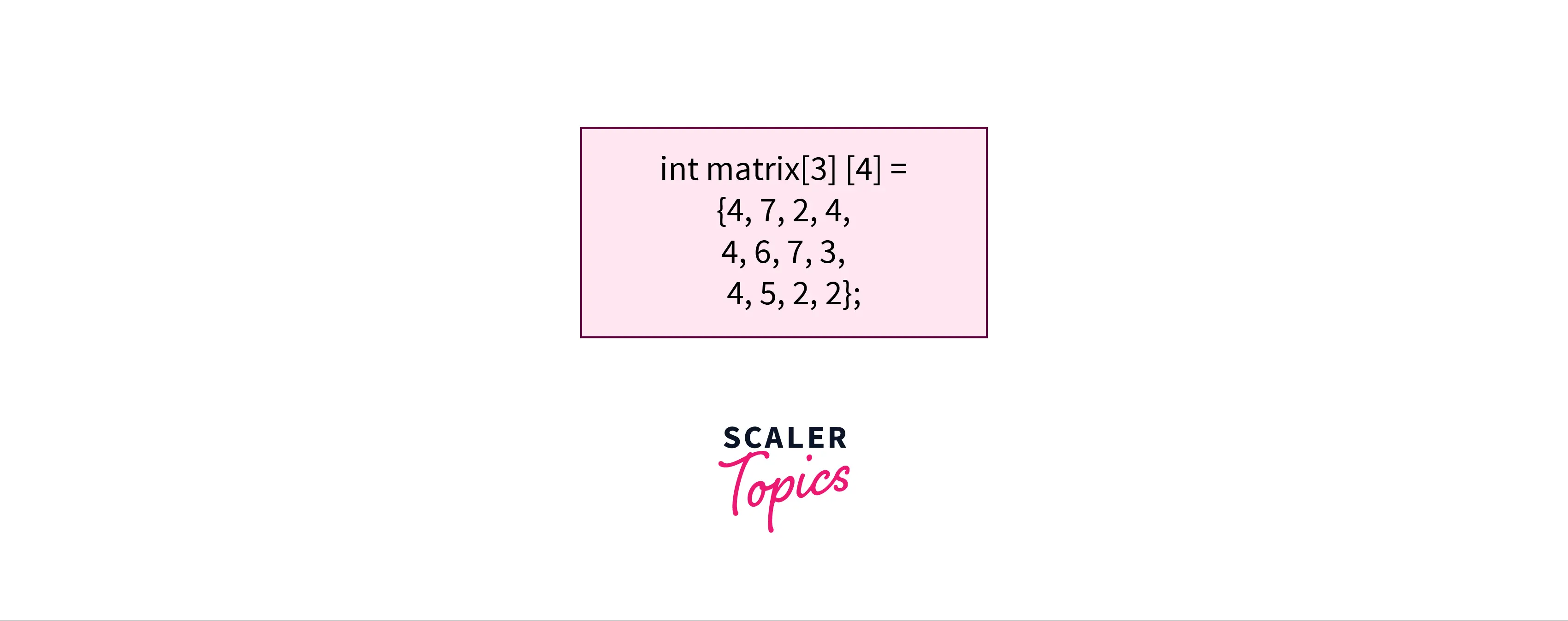
Later in this article, we will go over various functions and operations in NumPy matrices that help us to perform calculations faster.
Matrix Library in NumPy
Suppose we have to multiply two matrices. Normally, we will create two for loops, iterate through each element and store their product, and so on.
By using NumPy, we can simply call the .dot() function. This function will give us the dot product of our NumPy matrices.
Now, we will go over some of the technical aspects when it comes to NumPy matrices.
- numpy.matlib numpy.matlib is a Matrix library included in the NumPy package. Instead of ndarray objects (the general return type for arrays), this module's functions return NumPy matrices.
Syntax:
where the parameters are: data : input data dtype : data-type
This method will return a matrix based on our input.
output:
- numpy.matrix() This function will return a NumPy matrix, and can take inputs such as integers and strings of data. It also has certain mathematical functions like multiplication and power.
Note: This function is no longer recommended in the latest versions of matplotlib. You can choose the above mentioned .mat() function to create NumPy matrices.
Syntax:
where the parameters are: data : input data dtype : data-type
output
- numpy.asmatrix() To interpret a given input as a matrix, use the asmatrix() function. When the input is already a matrix or an ndarray, asmatrix does not create a copy as a NumPy matrix does.
Syntax:
where the parameters are: data : input data dtype : data-type
This method will return any data-structure as a matrix
output:
- numpy.copy() The numpy.copy() allows us to copy the contents of one NumPy matrix in another variable.
Syntax:
where the parameters are: data : input data order : Controls memory layout
This method will return any data-structure as a matrix
output:
- numpy.bmat() This function returns specialised 2-D matrices from nested objects, which may take the form of strings or arrays.
Syntax:
where the parameter is: object : Can be arrays or strings
This method will return arrays or strings as a two-dimensional matrix
output:
Replacement Functions in Matlib
Replacement functions in Matlib are the functions that are used to build or replace values in a two-dimensional NumPy matrix.
There are several methods to use replacement functions; for example, we could generate a NumPy matrix with all the elements set to 1, an identity matrix, a random matrix, etc.
Replacement functions are designed to make manipulations on NumPy matrix easier. They're a range of pre-defined functions for replacing/creating values in a two-dimensional matrix.
In this section, we will go over the eight most utilized replacement functions in NumPy. Let us look at each of them --
- numpy.empty() This function returns a new array of the specified form and type, with no entries initialized.
Syntax:
where the parameters are: data : input array
output:
- numpy.zeros() This function returns a new NumPy matrix, filled with zeros, of the specified shape and type.
Syntax:
where the parameters are: shape : The shape of the array dtype : The type of data order : Whether multidimensional data should be stored in memory in row-major (C-style) or column-major (Fortran-style) order.
output:
- numpy.ones() This function returns a new NumPy matrix, filled with ones, of the specified shape and type.
Syntax:
where the parameters are: shape : The shape of the array dtype : The type of data order : Whether multidimensional data should be stored in memory in row-major (C-style) or column-major (Fortran-style) order.
output:
- numpy.eye() This function returns a two-dimensional array with zeros on the diagonal and ones everywhere else.
Syntax:
where the parameters are: N : Number of rows in the output M : Number of columns in the output. k : Index of the diagonal.
output:
- numpy.identity() This function returns an identity matrix. An identity array is a square array with the major diagonal filled with ones. Syntax:
where the parameters are: N : Number of rows and columns in the output dtype : data-type
output:
- numpy.matlib.repmat() This function repeats a zero-dimension to a two-dimension array or matrix MxN times.
Syntax:
where the parameters are: a : Array to be repeated m, n : The number of times "a" is repeated in the matrix.
output:
- numpy.random.rand() This function returns an array of the provided shape with random samples from a uniform distribution throughout the range [0, 1]. The values of this array will lie between 0 and 1 only.
Syntax:
where the parameters are: d : The returned array's dimensions
output:
- numpy.random.randn()
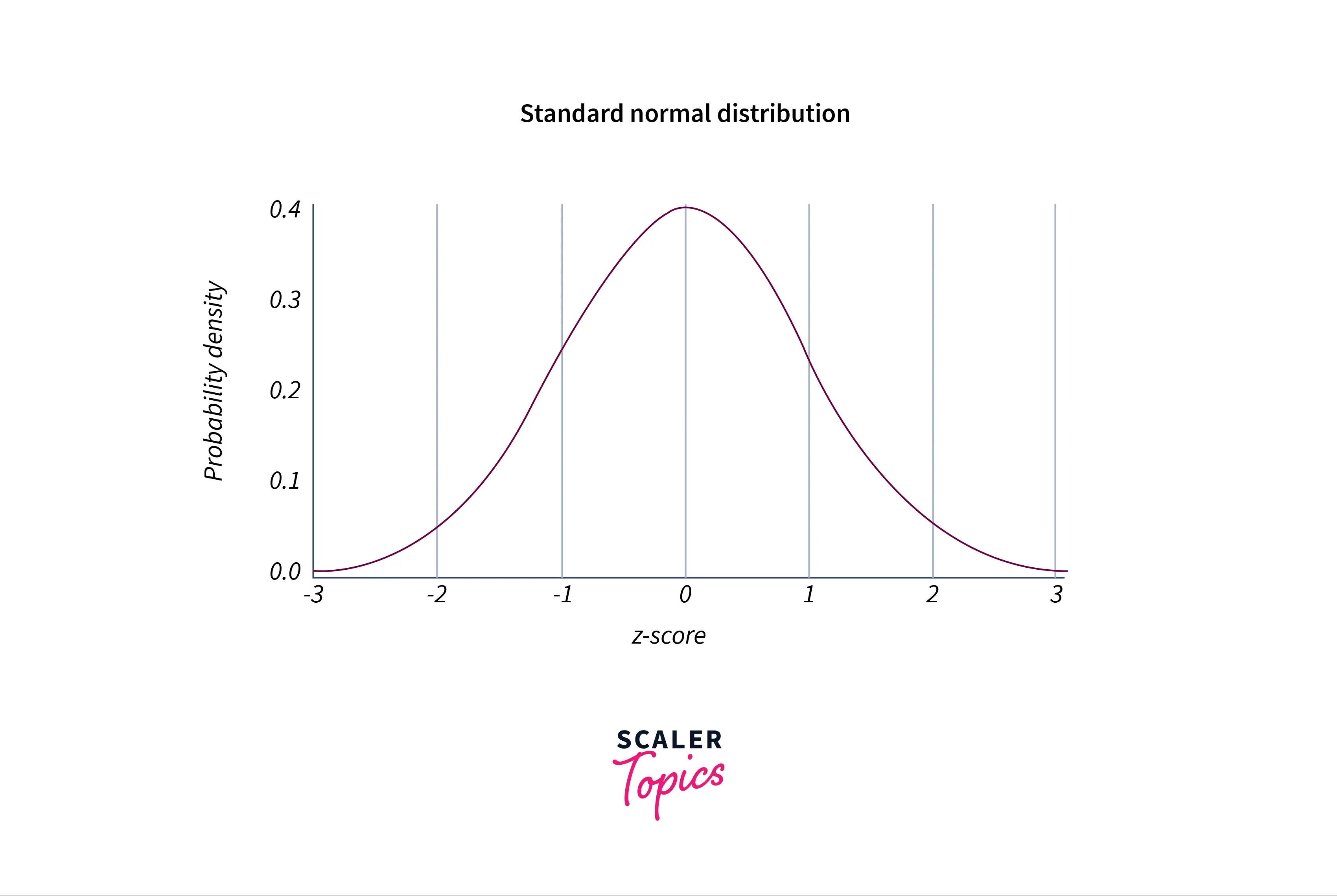
This function returns a value from the "standard normal distribution".
A standard normal distribution is a special distribution where the mean is 0 and the standard deviation is 1.
A general standard normal distribution looks something like this:
The values of this array will lie between 0 and 1 only.
Syntax:
where the parameters are: d0, d1, dn : Dimensions of the array to be returned.
output:
Conclusion
Let's recollect the topics that we covered in this article:
- A NumPy matrix is a two-dimensional table, which has specific number of rows and columns.
- There are a bunch of important operations performed on NumPy matrices, some of them being .copy() (copies the entire matrix) and .dot() (calculates the dot product of two matrices).
- We understood functions like bmat() and asmatrix(), which help us convert any data-structure into a NumPy matrix.
- We learned about replacement functions in matlib; which help us to build/replace values in a two-dimensional NumPy matrix.
- Apart from this, we understood functions like identity() that helps us create identity matrices, rand() which generates random two-dimensional NumPy matrices, and ones() that creates a NumPy matrix containing only 1.