Program for Pascal’s Triangle in Java

How to Print Pascal’s Triangle in Java

Pascal's triangle in Java is an array that resembles a triangle such that the size of each row is larger than the previous row. Pascal's triangle is named after the famous mathematician Blaise Pascal. There are multiple ways to build this triangle.

Approach #1

The first approach to print Pascal's Triangle in Java is using the binomial coefficient formula. The binomial coefficients are used to find the number of ways we can make a selection of a certain number of items from the provided pool of items without the consideration of order. It is commonly known as $^nC_r$ formula.

$^nC_r = \frac {n!}{(n-r)!r!}$

where n! represents the factorial of n.

Now this formula can be used as follows to print the Pascals triangle:

for each $i^{th}$ row, we have i number of elements. n is always equal to the (i-1) and r ranges from 0 to n.

Refer to the below pseudo code for better understanding:

Let us say we wish to find Pascal's triangle for n = 3 and 4th row using the above pseudo-code:

Pascal's triangle formula is $^nC_r = \frac {n!}{(n-r)!r!}$ . For the $4^{th}$ row, the n becomes 3 as we start counting from 0. The value of k ranges from 0 to 3. So we are supposed to find $^3C_0$, $^3C_1$, $^3C_2$, $^3C_3$.

The first element in the 4th row is,

Similarly, the second element is:

Similarly, we get $^3C_2 = 3$ and $^3C_3 = 1$. These values can be printed as part of the Pascal's Triangle in Java.

This algorithm works well for small values of n but for larger values of n, the computations become complex, calculating factorials and storing them is a difficult task for larger values.

For example, for the 13th row, we are required to find the factorial of 13 which is equal to 6227020800. This cannot be stored in int data type as it exceeds its limits. Secondly, I need to divide it with another factorial which can be as large as this is. The second approach that we will discuss is capable of overcoming this limitation.

Algorithm

The algorithm to print Pascal's triangle in Java using the above method is given as follows:

• The height of the triangle is taken from the user as a parameter to the function let's say n. We will be printing n+1 rows for n as input.
• We will use the outer for loop having variable i starting from 0 to n. This will print rows one by one.
• Inside the outer iteration we will have two inner loops one for printing space and another for printing $^nC_r$. At the end of each iteration print the next line to print a new row on a new line.
• The first inner loop will print the spaces so it will have a variable j which starts from 0 to (n-i).
• The second loop will start from 0 to i and calculate $^iC_j$ in each itertaion and print it.
• We will be using a support function factorial and $^nC_r$ to make calculations clearer.

Implementation

Code:

Output:

Explanation:

We have created two separate functions to calculate factorial and ^n^Cr. The factorial function uses recursion to calculate the factorial of a number. nCr function simply applies the formula and calls the factorial function.

The function printPascalsTriangle() uses interaction to print Pascal's Triangle in Java that takes n as an input. The outer loop iterates from 0 to n i.e. (n+1) times and each iteration is responsible for printing a row from top to bottom. The first inner for loop is used to print leading spaces. The second inner loop prints $^nC_r$.

Complexity

The time complexity for the factorial function and nCr function is O(n). As we are using an outer for loop and an inner for loop in the printPascalsTriangle() function the time complexity is $O(N^2)$.

Approach #2

Another approach to finding Pascal's Triangle in Java is based on simple observation. Have a look at below diagram:

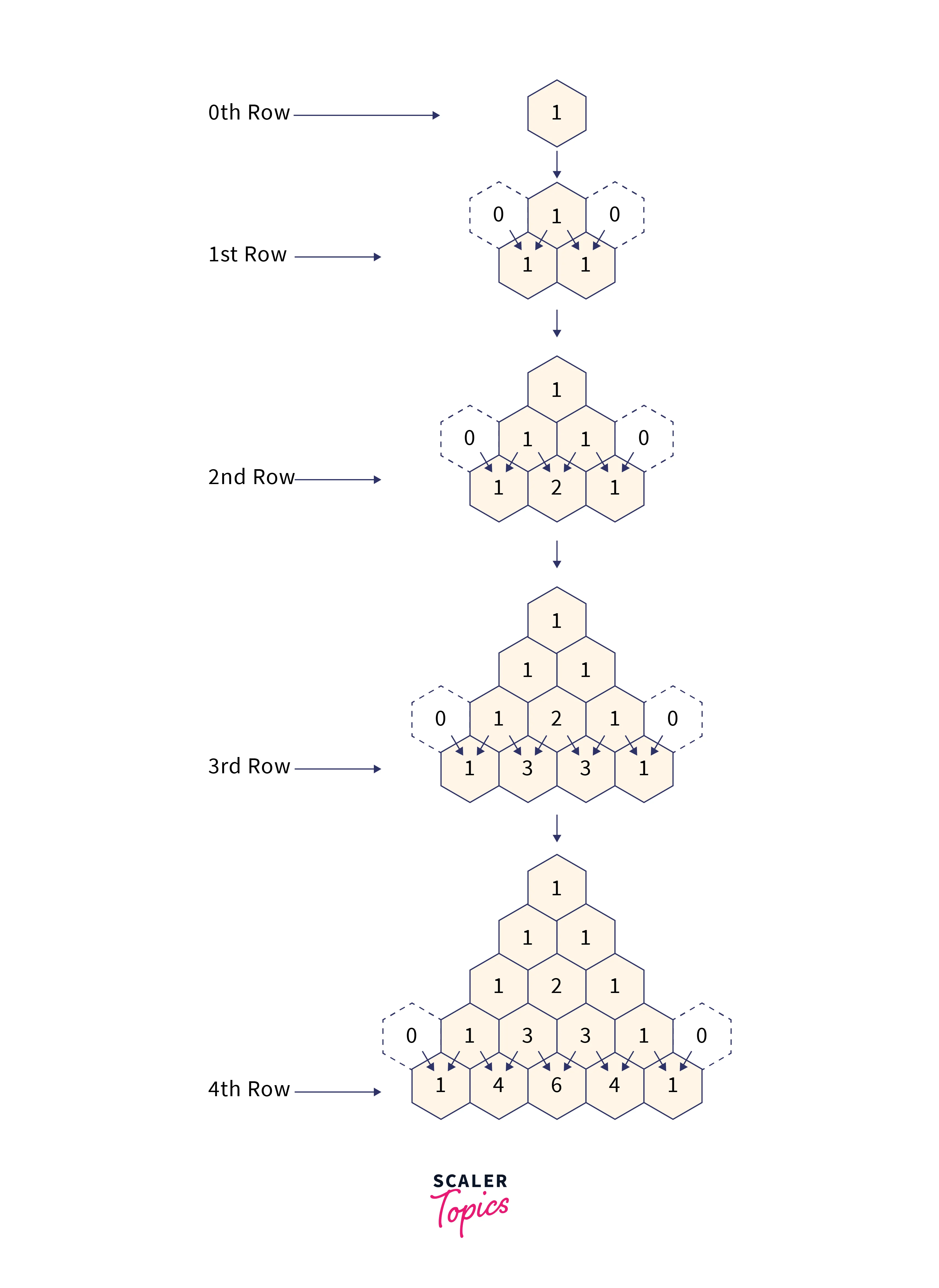
The empty spaces can be treated as zeros. The addition of the two numbers above gives the current value. This observation can also be useful for building Pascal's triangle in Java. Also, it reduces a lot of factorial calculations.

This approach is better than the previous approach in the case of larger values of n as it doesn't require large calculations of factorials. It only adds values used in previous rows, requires no complex computations as well, and can print triangles for a larger number of rows.

We can also extend this approach to dynamic programming in order to efficiently generate Pascal's Triangle in Java without calculating factorials.

Algorithm

The algorithm to implement the above approach is given below:

• $i^{th}$ entry in a row is a Binomial Coefficient C(row, i) and all the rows start with value 1.
• To calculate the C(row, i) the given formula is used: $C(row, i) = \frac{C~[~row, ~(i-1)]~ *~ [(row - i)~ +~ 1]}{ i}$
• The approach is similar to the above one only change is in the formula to calculate the value.
• We will again use the outer loop to print rows, the first inner loop to print spaces, and the second inner loop to print calculated values.

Implementation

Code:

Output:

Explanation:

Here, we are not using factorials or combinations. We are using the simple function printPascalsTriangle() that takes n as an input and prints n+1 rows in the output. The outer for loop iterates through each row. The first inner loop prints the leading spaces for formatting.

Before the second inner loop variable C is initialized by 1. This represents the value of "n choose i" (C(row, i)). Another inner loop (i loop) calculates and prints the values for the current line using the combination formula C(row, i) and updates the value of C for the next iteration.

Complexity

Again two nested loops are used to find Pascal's Triangle in Java thus, time complexity remains the same as the above approach i.e. $O(N^2)$. The auxiliary space complexity is O(1) as this time we are not using recursion or any external calculations.