Pascal Triangle in Python

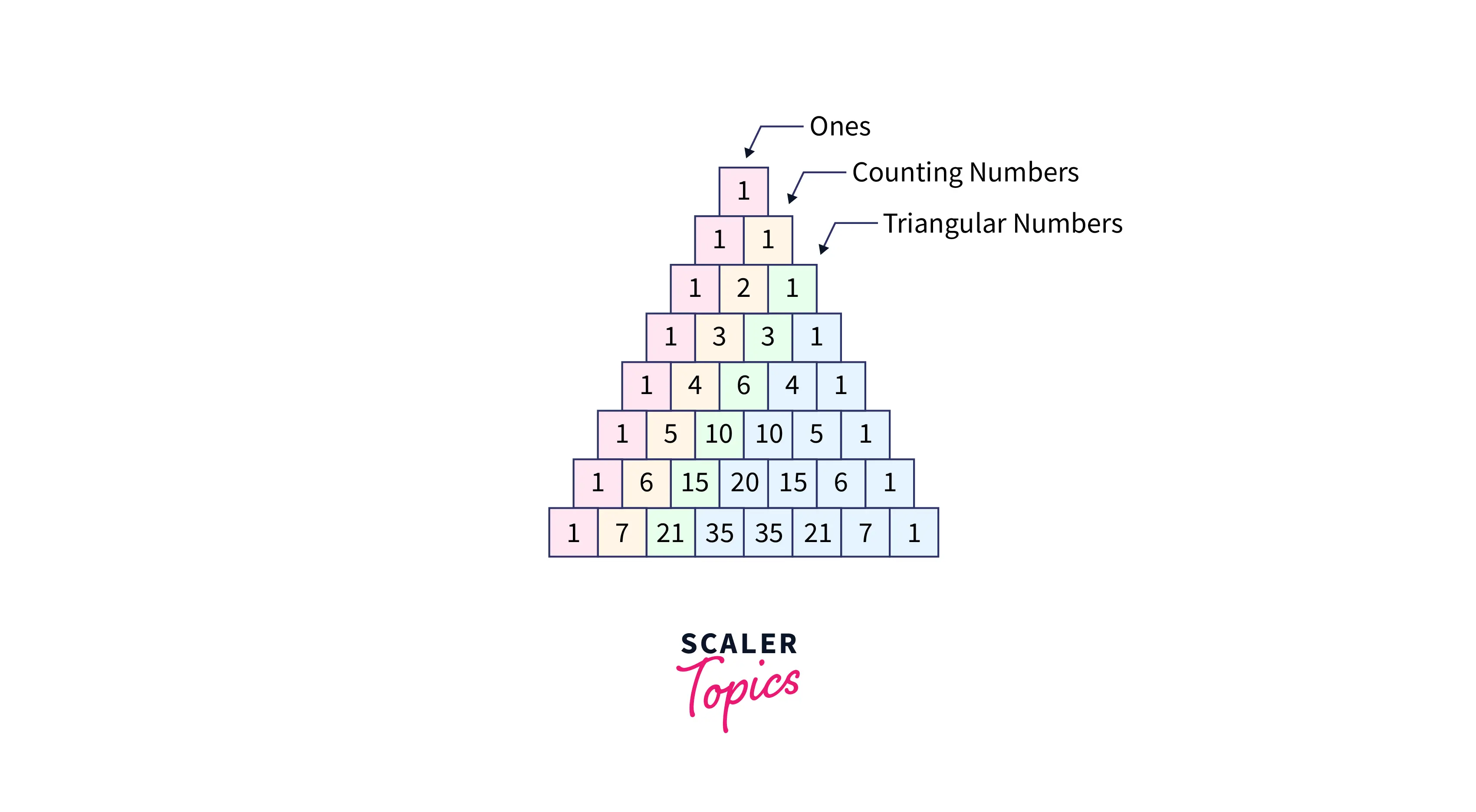
What is Pascal Triangle?

Pascal's triangle has been given its name after the famous French mathematician Blaise Pascal. The classic definition of Pascal’s triangle is given as a number pattern where the numbers are assembled in the shape of a triangle. This triangular pattern has the periphery as 1 and the inner values of the triangle are obtained by adding the adjacent row according to the mathematical concept of pascal traingle.

We shall be implementing python logic to create the pascal triangle as we move ahead in the module.

The below diagram explains how we can create the pascal triangle in python.

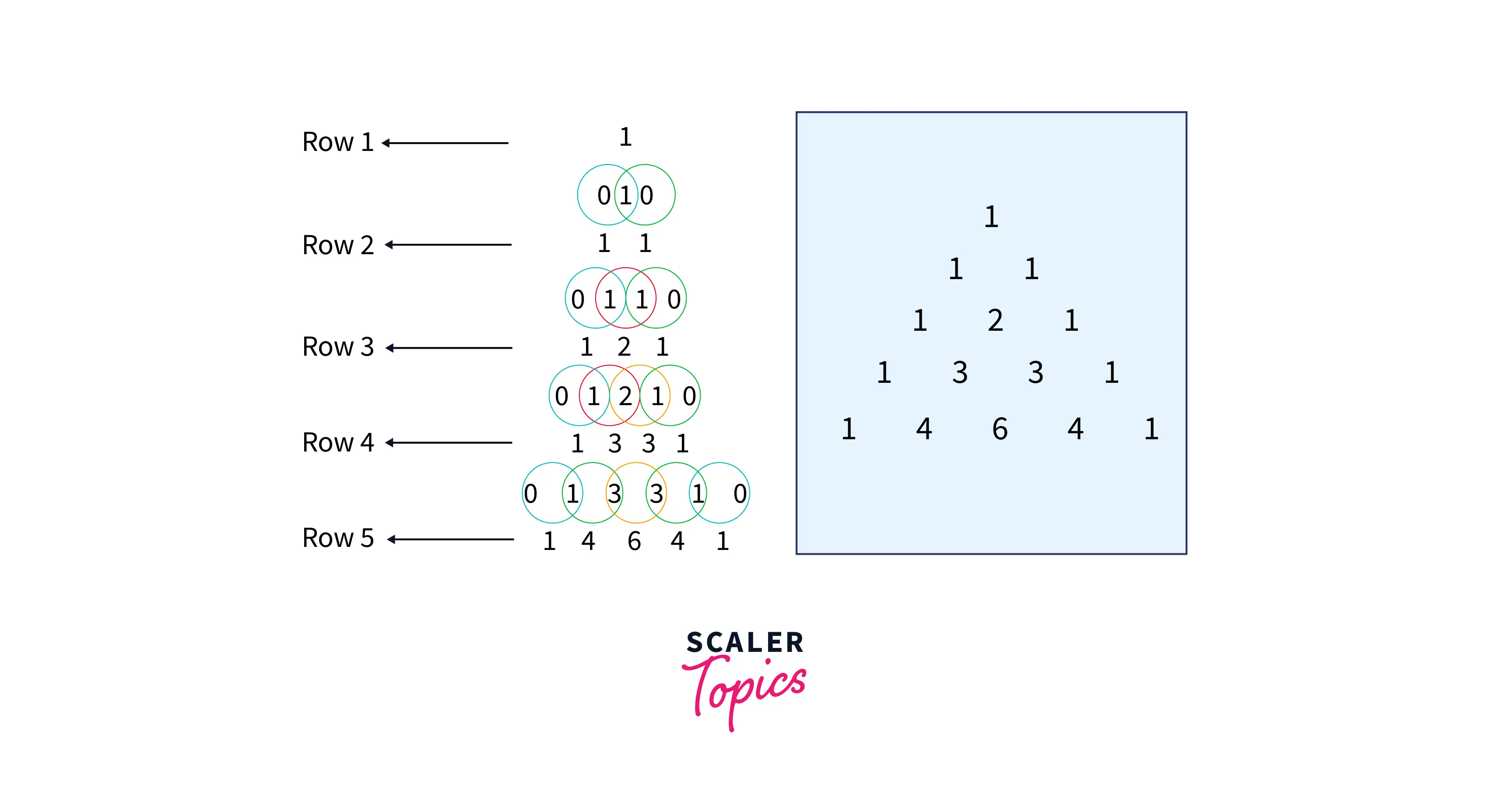
As seen in the above diagram, we see that the outer periphery of the triangle is only having the number 1 whereas in the inner edges of the train the numbers are formed or generated by actually adding the adjacent rows.

Let us walk through the diagram where the first row is 1. Then, the second row contains 2 one, proceeding to the third row having 1 2 1, where the number 2 was obtained by taking up the addition of the above row as shown in the diagram. And hence this alternate pattern is repeated in the entire triangle and so on.

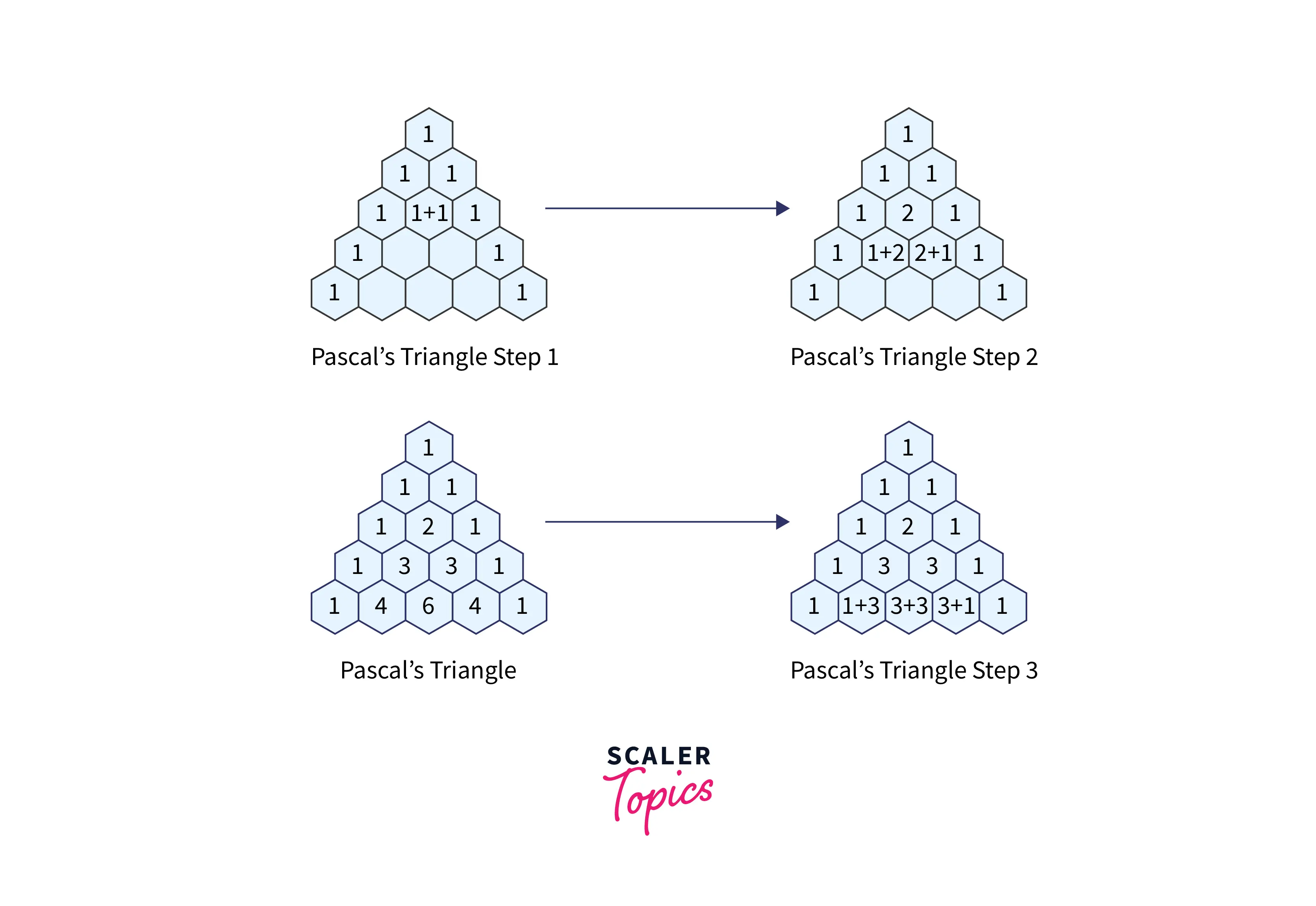
The below diagram explains the pictorial representation of what a pascal triangle in python looks like:

Algorithm to Print Pascal's Triangle in Python

The way in which we shall be using python language to create the pascal triangle is fairly simply. The intution we keep to proceed with algorithm is that we start by printing the row by row and keeoing in mind that the periphery of the triangle is to be kept 1. Also, the inner values are to be obtained by adding the adjacent row values.

Before we jump into different methods to construct the Pascal Triangle in Python, let us first understand the algorithm that is followed:

Step 1: First, we get the number of rows which is taken as input from the user, followed by storing the values in an empty list.

Step 2: With the help of for loop in python we then iterate from 0 to n - 1 and keep on appending the values to the list. For example, first we apend 1 to the list and so on.

Step 3: We then make use of the for loop in python to print the number that would be present inside the triangle that are obatined by simply adding the values in its adjacent row.

Step 4: Now we will be able to print the pascal triangle as specified in the above format.

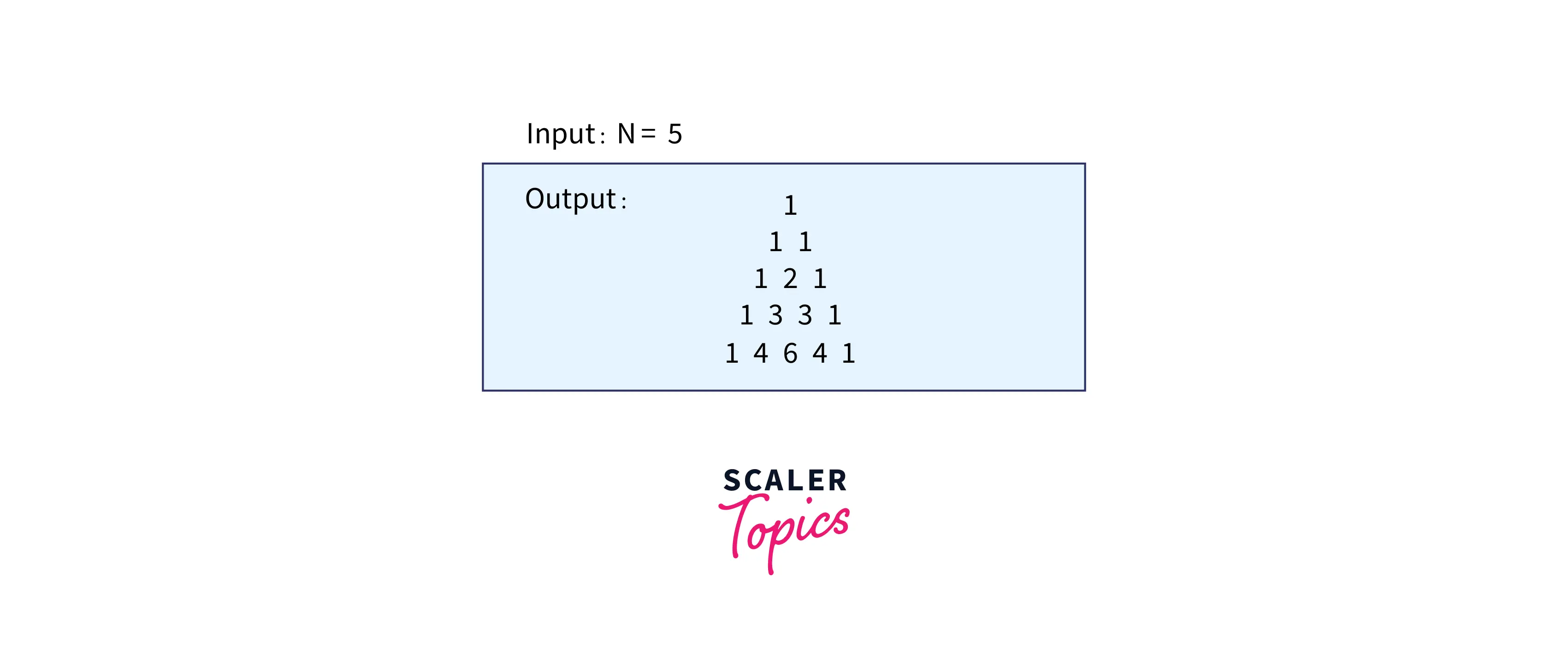
The below diagram depicts how the input is taken from the user and the output we get is the pascal triangle in python.

Method 1: Using nCr Formula i.e. $n!/(n-r)!r!$

To construct the pascal triangle in python, the basic method that can be used is to make use of the combination concept from mathematics.

We can obtain the entry of the numbers in the pascal triangle by using the combination formula nCr where nCr elaborates the number of ways we can choose the r elaborates on the number of elements from a bunch of n elements.

The formula can be explored more as below:

$n C r=\frac{n !}{(n-r) ! r !}$

where, n !=n(n-1)(n-2) \ldots 3.2 .1

Code:

Output:

Time complexity: The time complexity for this method is obatined as $O(N^2)$

Explanation:

In the above code, we have started by taking the input from the user for the number of rows for which the pascal triangle in python could be generated. Then we import the factorial from the math module. Using two for loops we have created the structure of the triangle and we print spaces on the left while starting a new line to make it look like a triangle. We have also used the nCr formula to take the factorial of each number as suggested by the combination formula.

Method 2: Binomial Coefficient

Now let us apply the fundamentals of the** binomial coefficient** to print the pascal triangle in python where the nth number in a row is equal to the Binomial Coefficient and every line of these rows contains the number 1.

While studying the mathematical concept of the binomial coefficient, we might have used the following formula,

Binomial_Coeff = C(row(r), l-1) * (row(r) - l + 1) / l

where the r’th entry in a row number row is the Binomial Coefficient C(row, r) and all the rows start with value 1. The idea is to calculate C(row, r) using C(row, r-1).

We make use of the binomial coefficient to print the pascal triangle as the pascal triangle that is formed has the values which are similar to the coeffcient values that could be otained from the binomial theorem.

As seen in below diagram we see that each row has values that are equal to the binomial coefficient:

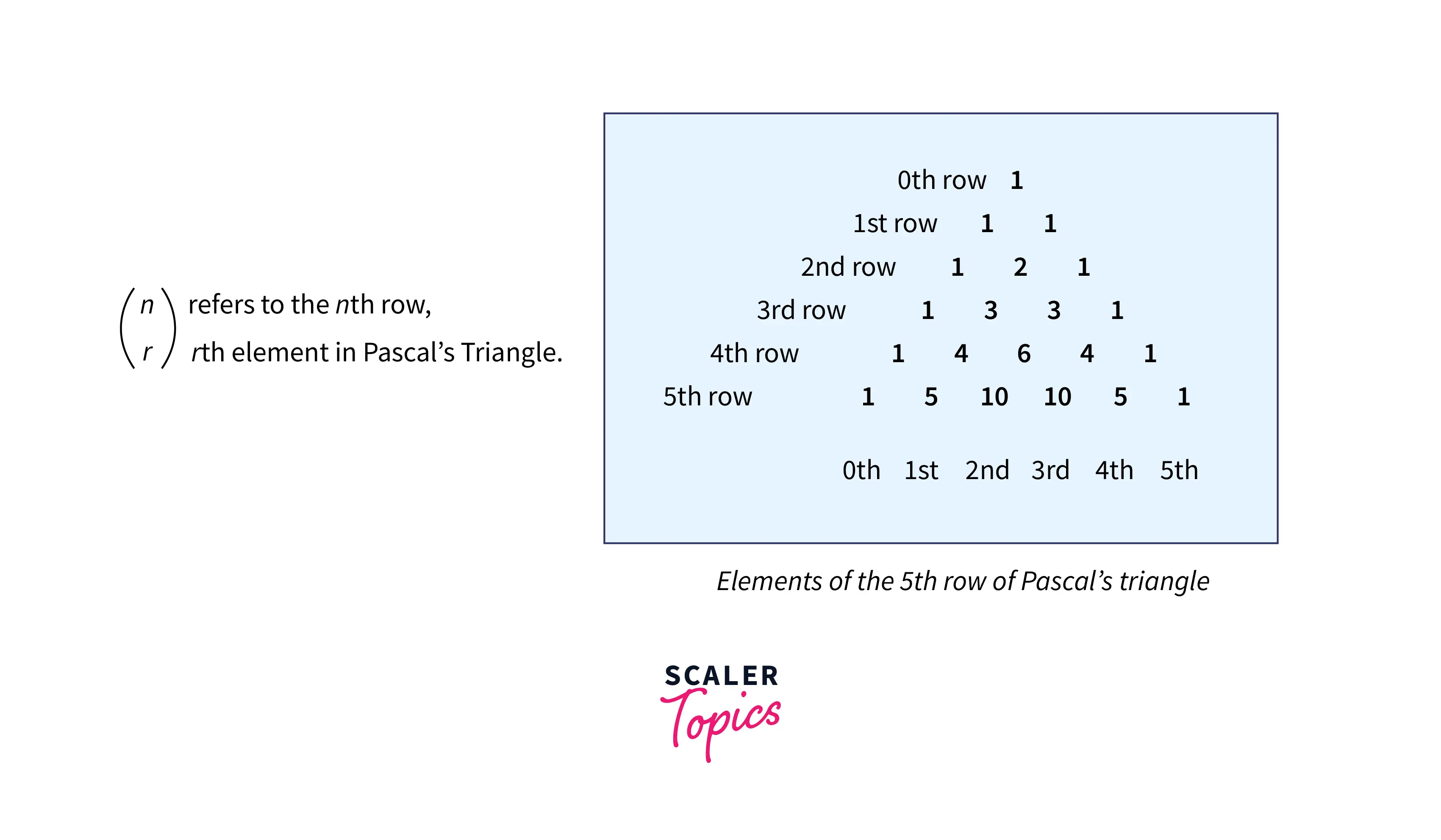
Code:

Output:

Time complexity: The time complexity for this method is obatined as $O(N^2)$

Explanation:

In the above code, we have started by taking the input from the user for the number of rows for which the pascal triangle in python shoeuld is generated. Then we are using two for loops in python to iterate the rows accordingly. Also, as we studied that the pascal triangle formed by the Binomial coefficient formula is a triangle containing umber 1 in outer and inner edges, we took the constant B as 1 and used a for loop to again start s=forming rows having spaces in the left and right to form a triangle pattern. Lastly, we make use of the Binomial coefficient formula to print the pascal triangle in python.

Method 3: Based on the Power of 11

The most optimal way to construct a pascal triangle in python for the number of rows under five is by using the power of 11 method.

To print the pascal triangle in python, the most straightforward technique to print the pattern containing less than five rows is the The power of the 11 method. It explains how the incrementing values of the power on the number 11 follows the property mentioned in the Pascal Triangle pattern.

Explore below how the multiplication table of 11 plays out, it gives a picture of exactly how we define the pascal tringle in mathematical terms.

The below diagram shows the pictorial representation of what we want our pascal triangle to look like.

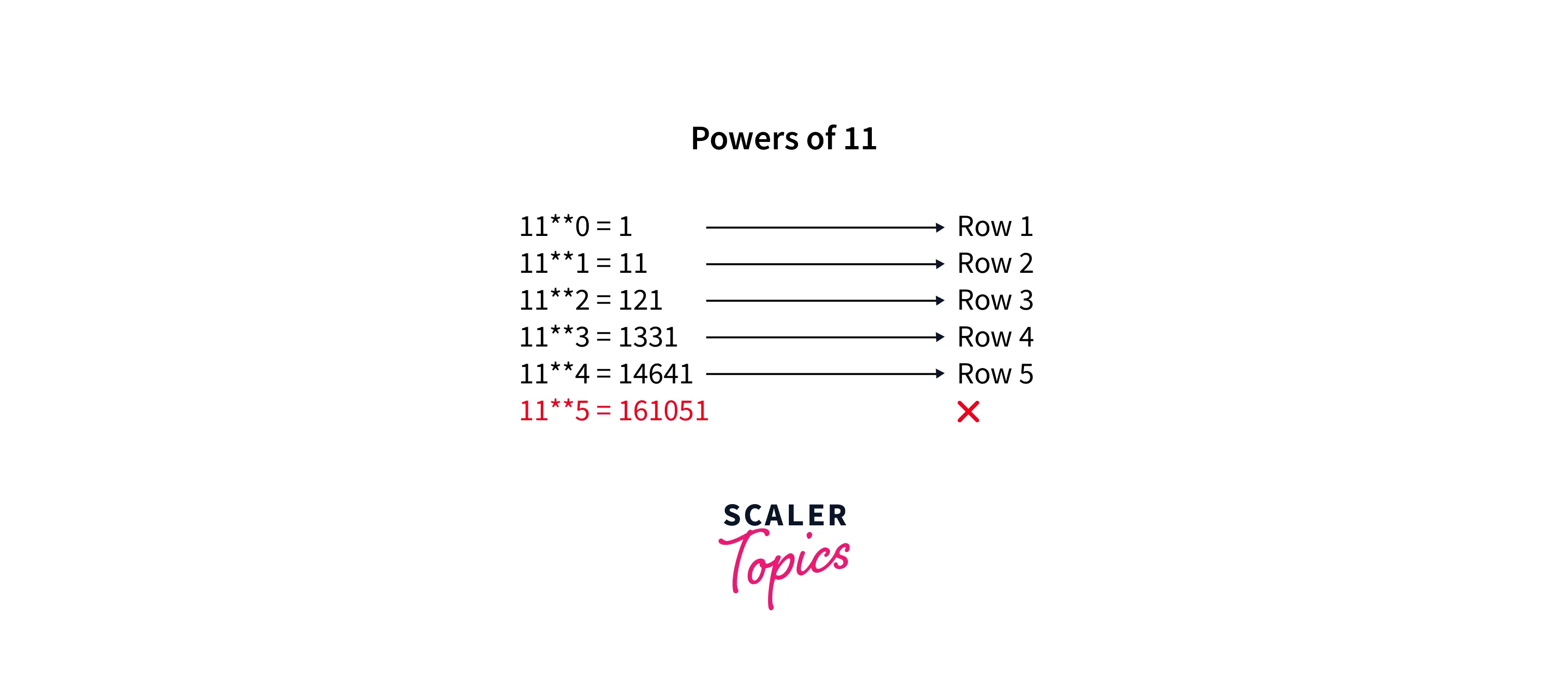
Notice that beyond four it starts to disorient in a way that does not fit into the property specified for constructing the pascal triangle. That means 11 raised to powers {0, 1, 2, 3, 4} give the output that follows the property of Pascal’s triangle.

Code:

Output:

Time Complexity: The time complexity for this method is obatined as O(N)

Explanation:

In the above code, we have started by taking the input from the user for the number of rows (max 5) for which the pascal triangle in python would be generated. Now we use 1 for loop in python to print the numbers with spaces left on the left side to make it look like a triangle. We also made use of the join() method to join the elements. By default the powers of 11 are integers, we also convert them to a string using the str() method.