Permutation of String in Java

Introduction

We all have studied the theory of Permutation and Combination topic in our school-level books. Still, we have you ever wondered if we can practically calculate and find all those permutations of string in Java?

Just to recall the theory and basics, permutations of string mean finding all the possible new arrangements of the string by interchanging the position of characters of the original string.

Example:
string ABC has 6 permutations - [ABC, ACB, BAC, BCA, CAB, CBA]

The number of permutations of a string is always equal to the factorial of the length of the string.

For example:
string HELLO of length 5 has 5! permutations i.e. 120 permutations in total. We will not manually write all 120 permutations here, but this can be quickly done using Java programming.

We have two methods to generate all the permutations of string in Java that we will learn as we go through the course of this article :

• Recursive Approach
• Iterative Approach

Java Programs to Generate All the Permutations of a String

1. Recursive Approach

Since strings in Java are immutable and can't be changed or modified, the simple idea is to convert the string into a character array to generate its permutations. We can use the concept of Backtracking by swapping each of the remaining characters of the string with its first character and generating all the permutations of the remaining characters using a recursive call.

For better understanding, we will illustrate it using Java Program below:

Example - 1

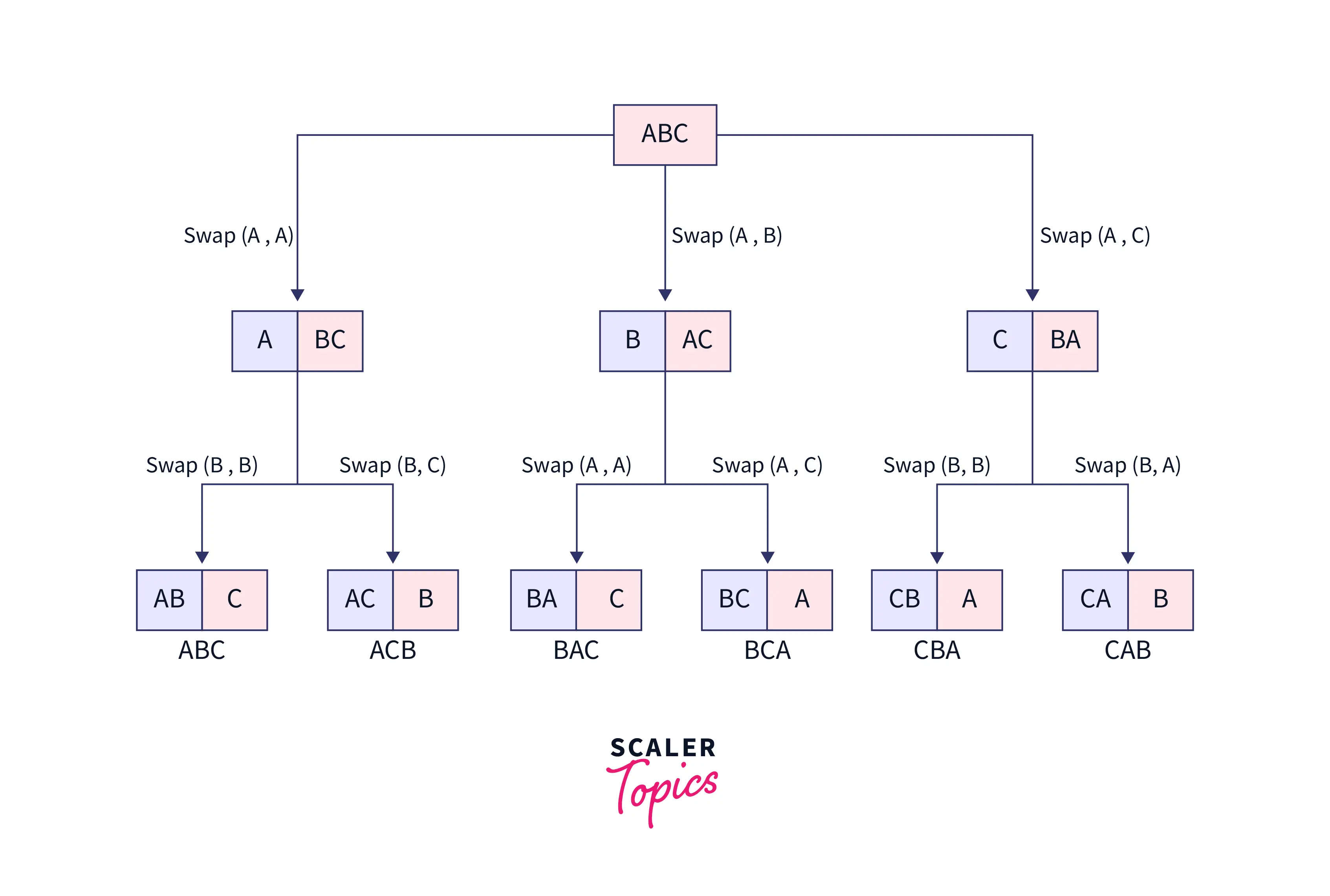
In this Java Program, we will print all the possible permutations of string using a recursion or backtracking approach. The entered string will be converted into a character array using the toCharArray() function and will be passed into the solve function. The simple idea is to swap the character array values with the passed index character element to keep a track of the arrangement of the string and then call the solve function again recursively to solve for the (index+1) value.

The base condition is encountered when the currently passed index value becomes equal to (arr.length - 1); hence, we will print the resultant array as one possible permutation of a string. To print all possible permutations, we will again swap to get back the original values in the for loop after the recursive call. This is backtracking, and in this way, the current character element can be used further in other possible string arrangements.

Output :
The output clearly shows all 6 possible permutations of the entered string : "ABC"

Recursion Tree for printing all the permutations of string "ABC" in Java :

Example - 2

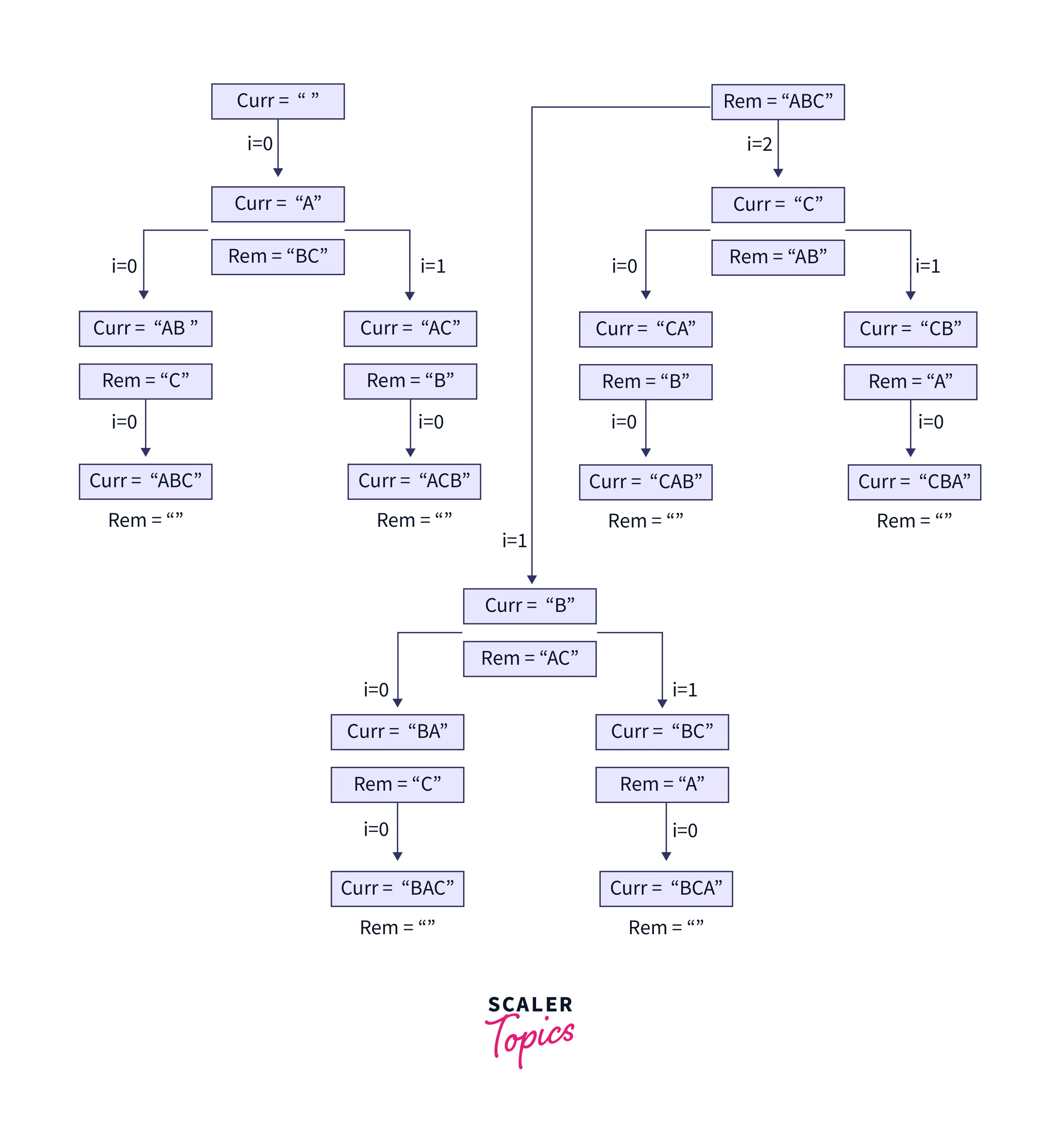
If we don't want to convert a string into a character array, we have another recursive implementation for generating all the string permutations in Java.

In this Java program, we have a recursion faith that the solve() function will calculate all the possible arrangements for the remaining characters of the string, and we are adding the current index character to the curr string. When the base condition is encountered where the length of the remaining string becomes 0, we will print the arrangement as a valid permutation.

Output :
The output clearly shows all 3! i.e. 6 possible permutations of the entered string : "ABC"

2. Iterative Approach

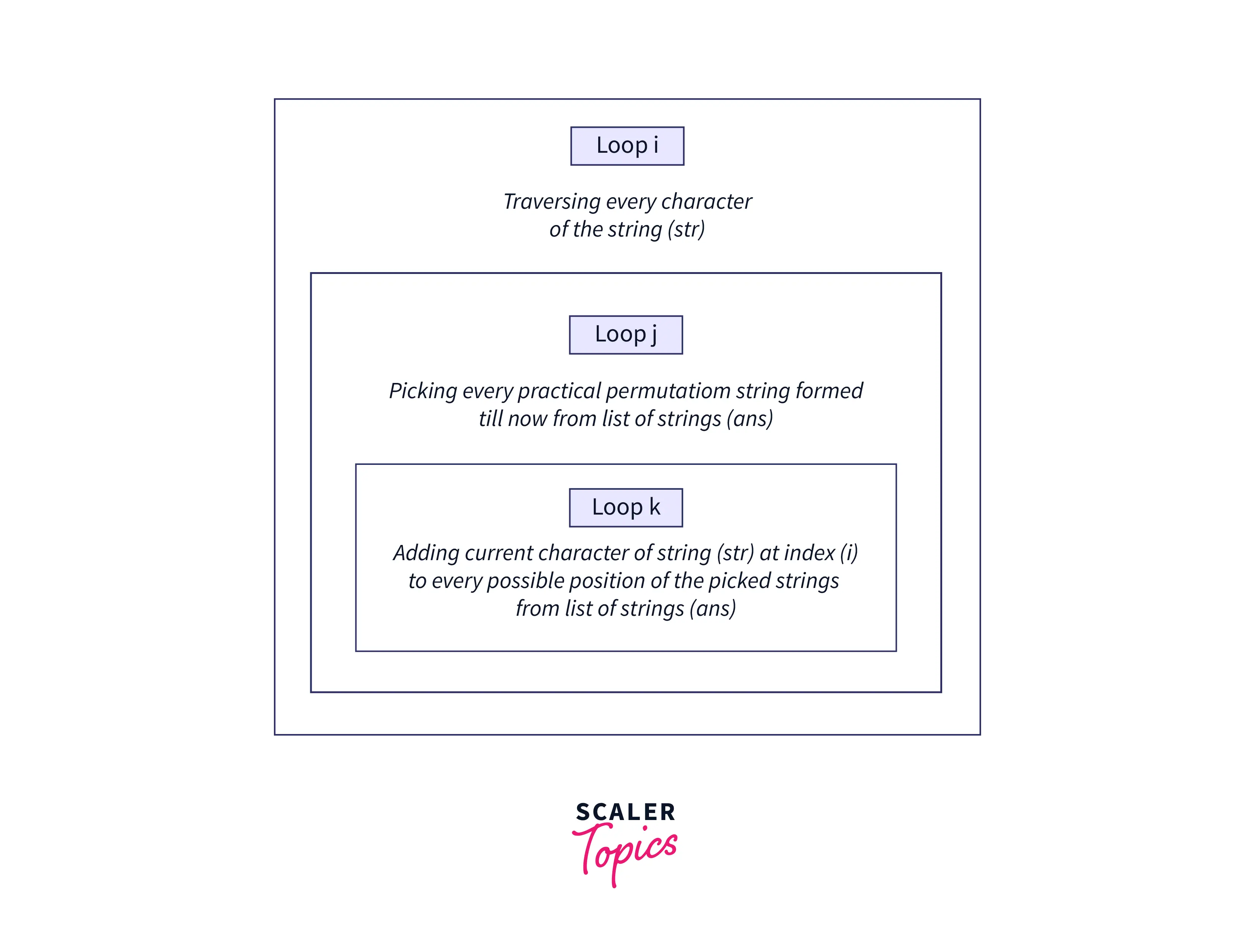
To generate all the permutations of string in Java iteratively, we will use ArrayList, which will contain the partial permutations initially, and using that, we will get all the arrangements in the end constructively.

In this program, we have created an empty ArrayList and initialized it with the string's first character. The idea is to use previously constructed partial permutations one by one for each character of the specified string. We will remove the current partial permutation from the ArrayList and insert the next character of the specified string at all possible positions of the current partial permutation. The newly constructed string will then be added to the ArrayList, and this process will be continued to find all the possible permutations.

Output :
The output clearly shows all 3! i.e. 6 possible permutations of the entered string : "ABC"

Distinct Permutations of String in Java

Recursive Approach (Using Boolean Array)

This Java program uses the same recursive approach that we studied above, but we have made slight modifications to identify and print only the distinct permutations of string. We have used a boolean array that accounts for the character being used. If the character hasn't been used, then it will make a recursive call. The base condition is encountered when the passed string is empty.

Output:
The output clearly shows all the distinct permutations of the entered string: "REEL"

Recursive Approach (Using HashSet)

In this Java program, we will use HashSet, which will only contain the distinct string permutations and no duplicate arrangement. The idea is the same: we are using a recursive approach and will add all possible accounts to the set.

Output:
The output clearly shows all the distinct permutations of the entered string: "BELL"