Peterson's Solution

What is Peterson's Solution in OS?

Peterson's solution is a classic solution to the critical section problem. The critical section problem ensures that no two processes change or modify a resource's value simultaneously.

For example, let int a=5, and there are two processes p1 and p2 that can modify the value of a. p1 adds 2 to a a=a+2 and p2 multiplies a with 2, a=a*2. If both processes modify the value of a at the same time, then a value depends on the order of execution of the process. If p1 executes first, a will be 14; if p2 executes first, a will be 12. This change of values due to access by two processes at a time is the cause of the critical section problem.

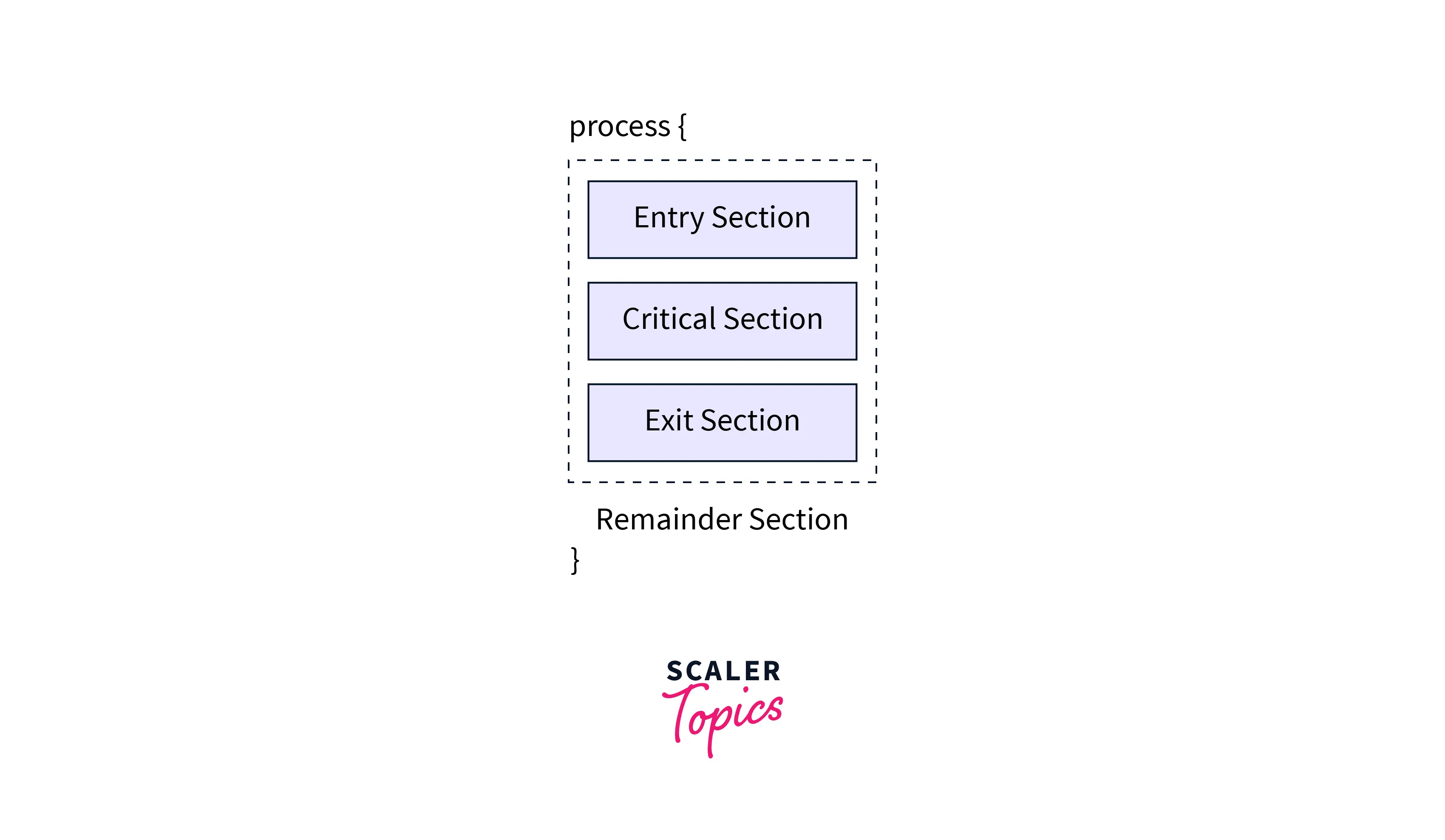
The section in which the values are being modified is called the critical section. There are three sections except for the critical sections: the entry section,exit section, and the reminder section.

• The process entering the critical region must pass the entry region in which they request entry to the critical section.
• The process exiting the critical section must pass the exit region.
• The remaining code left after execution is in the remainder section.

Peterson's solution provides a solution to the following problems,

• It ensures that if a process is in the critical section, no other process must be allowed to enter it. This property is termed mutual exclusion.
• If more than one process wants to enter the critical section, the process that should enter the critical region first must be established. This is termed progress.
• There is a limit to the number of requests that processors can make to enter the critical region, provided that a process has already requested to enter and is waiting. This is termed bounding.
• It provides platform neutrality as this solution is developed to run in user mode, which doesn't require any permission from the kernel.

Pseudocode for Peterson's Algorithm

The algorithm used for implementing Peterson's algorithm can be written in pseudocode as follows,

Explanation of Peterson’s Algorithm in OS

Let us see how the code above works in detail:-

• There are total N processes, each with a variable flag set to false on initialization. This variable flag indicates if a process is ready to enter the critical region.
• The turn variable denotes which process its turn is now to enter the critical region.
• Then, every process will enter the entry section in which we define j, which denotes another process that came before process i.
• We allow process I to enter the critical section and indicate that j process is now turned to enter the critical section using turn=j.
• Then we check whether the process j is in the critical region using the conditions flag[j]==true && turn=j. If process j is in the critical region, the while loop runs continuously, and stalls process i from entering the region until process j exits out of the critical region.
• The process which has exited the critical region is marked by flag[i]=false;, where I denote the process exiting from the critical region.

Implementation of Peterson's Algorithm using Programming Language

Typically the C programming language is used to implement Peterson's algorithm in OS, as the basic OS programs were written in C or C++.

Before getting into the example, we must understand how to create a shared region in memory that will act as a critical region. The shared memory can be created with the shmget() function with syntax,

The identifier is associated with the shared memory segment, and the storage_space is the amount of space needed for storage. The flags tell us the permissions and type for the shared memory. The IPC_CREAT | 06660 flag creates a new shared memory if it doesn't exist and gives read and write permissions.

We can access a shared memory using the shmat() function.

syntax:

The id is the value returned from the shmget() function, and the address is used to identify an address within the segment and a NULL value will give the first address in the shared memory. The flags are for permission.

The srand() and rand() functions are used to get random numbers based on time. The srand() function marks the start of numbers for generating random numbers using the rand() function.

Syntax:

The time is obtained using gettimeofday(); function with syntax,

Then the seconds are obtained from the default variable present in the time structure, time.tv_sec.

The implementation of Peterson's Algorithm using the C programming language to solve the producer-consumer problem is as follows,

• A shared memory accessed by both processes is the critical section.
• The entry section is the state before producing or consuming products.
• The exit section is the state after producing or consuming the products.
• If there are no products, the consumer is locked in the while (flag[i] == true && *turn == i); condition.
• The index is used to identify the positions of the products in the array and to check if the size of the array is lesser than the array's capacity.
• The variable current_state is used to check if the process waits too long. A value 0 represents they spend too much time waiting.
• The fork() system call creates the producer and consumer processes. It has the syntax,
• Syntax:

It returns a positive number on successful creation and a negative number when failed to create processes.

• A buf array is used to hold all the products, and computations are performed when a new product is produced or consumed.

Example of Peterson’s Solution

Peterson's solution finds applications and examples of different problems in Operating Systems.

• The producer-consumer problem can be solved using Peterson's solution. Learn more about how synchronization is maintained in producer-consumer problems.
• The logic used in a semaphore is similar to Peterson's solution. The semaphores are used to solve many problems in OS.
• The most suited example is the usage of Peterson's solution in the critical section problem.

Advantages of Peterson’s Solution

• Peterson's solution allows multiple processes to share and access a resource without conflict between the resources.
• Every process gets a chance of execution.
• It is simple to implement and uses simple and powerful logic.
• It can be used in any hardware as it is completely software dependent and executed in the user mode.
• Prevents the possibility of a deadlock.

Disadvantages of Peterson’s Solution

• The process may take a long time to wait for the other processes to come out of the critical region. It is termed as Busy waiting.
• This algorithm may not work on systems having multiple CPUs.
• The Peterson solution is restricted to only two processes at a time.