Prime Number Between Given Range in Java

Introduction

A number that is divisible by only 1 and itself is called a prime number. A prime number has only two factors.

To check whether the given number (say n) is prime or not, we can run a simple for loop from 2 to n - 1 using an iterator i and check whether the number n is divisible at each by i or not.

If n is divisible by i then the number is composite, or else it is prime. Executing a loop from 2 to number n takes around n iterations, so the time complexity to check whether the number is prime will be $O(N)$.

In this article, we will reduce the time complexity upto for the above algorithm up to $O(sqrt(n))$.

To find all prime numbers between two given numbers L and R, we can run a for loop from L to R (using an iterator i). For every number from L to R check whether the number is prime. If the number is prime print the number.

Time Complexity:

• To check whether the number is prime or not takes around $O(N)$ time using the algorithm we discussed above, where N is the number.
• To find all the prime numbers between the given range will take a time of $O( (R - L) * sqrt(N) )$ (Here, R is the upper limit of the range and L is the lower limit of the range).
• This is because every number takes around $O(N)$ time.

Example1: Display all Prime Numbers Between Given Range

Let us see a program where we will find all the prime numbers between the given numbers L and R.

Approach:

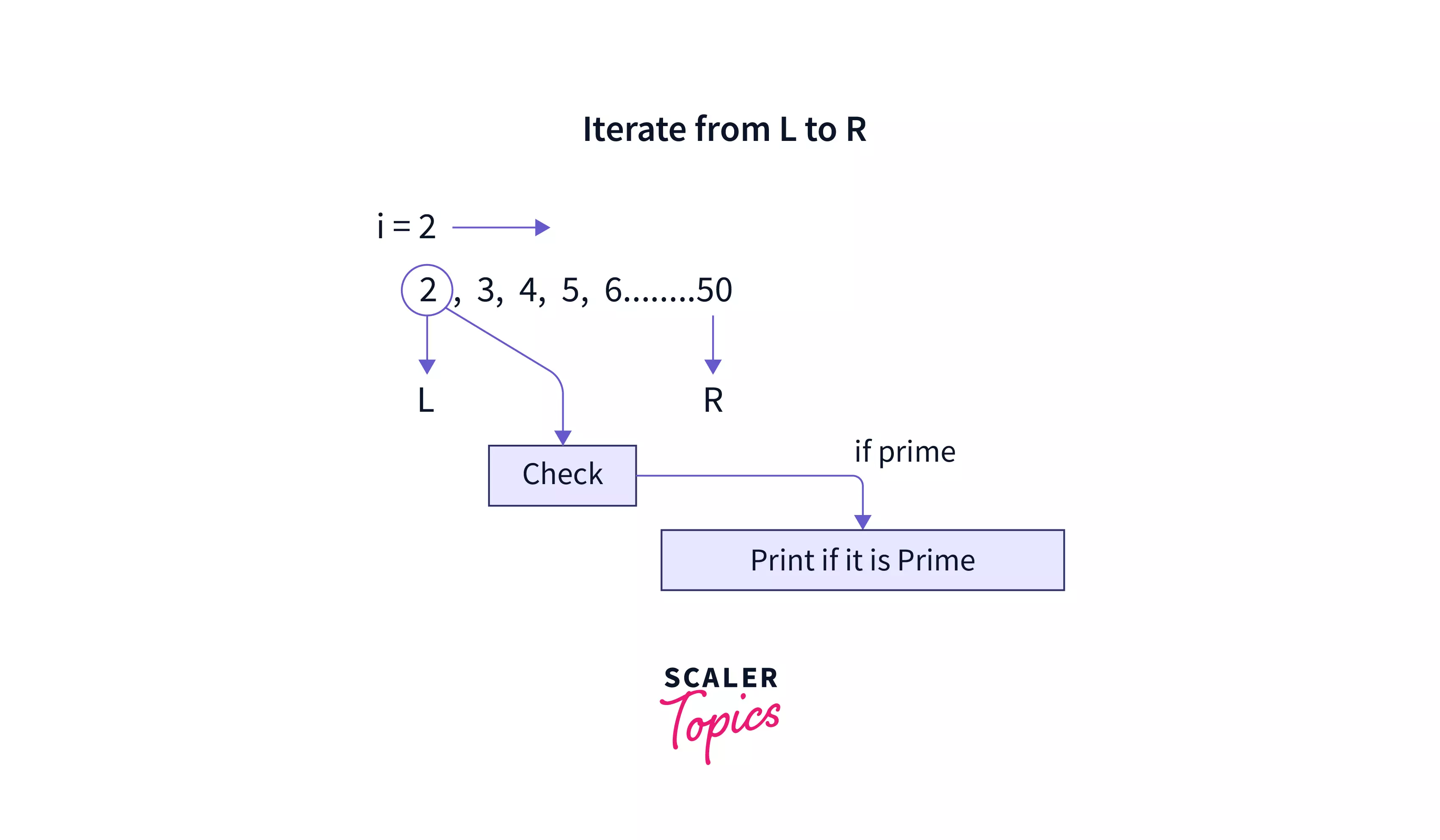
• We will run a loop from L ( Lower bound of an interval ) to R ( Upper bound of an interval ).
• For each number in the range from L to R, we will check whether the number is prime or not as shown in the figure below. Time Complexity: This will take a time of $O( N2 )$, considering N is approximately equal to L - R.

Code

Output

Explanation:

• In the above example, we are running a for loop from 2 to 50 at each iteration of i we are checking if the number is prime.
• We pass it to an isprime() function that takes an integer as a parameter to check whether the number is prime. In the isprime() function again, we are running a loop from 2 to the number n.
• If at any iteration from 2 to n if the number n is divisible by the iterator, then it returns -1, else it returns 1.

If the range of the given numbers (i.e. R - L) is comparable to the maximum number i.e. R, the overall time complexity of the algorithm above comes out to be $O(R^2)$ or $O(N^2)$.

Example 2: Display the Prime Numbers from 1 to 100

Reduce the Time Complexity of Prime Number Identification:

The time complexity of identifying a prime number can be reduced to $O(sqrt(N))$ using the observation that there must be atleast one factor a composite number N less than or equal to sqrt(N).

Proof:

• Let's assume that number n is not a prime, then it can be factorized into two factors x and y , i.e. n = x * y
• So, x and y cannot be both greater than the square root of n, since then the product x * y would be greater than sqrt(n) * sqrt(n) = n.
• Thus, in any factorization of n, at least one of the factors must be less than sqrt(n).
• In case we are unable to find any factors less than or equal to the square root, n must be a prime.

Approach:

• If the factor of a number N lies in the range from 1 to sqrt(N), the number is not prime, or else the number is prime.
• So, the required modification in example number 2 is to run for loop from 2 to sqrt(n).

Time Complexity:

The time complexity of the above code will be N * sqrt(N). For N numbers (in this case, N is 100), we need to run a loop from 1 to N. For each number, it takes sqrt(N) time. So, the total complexity will be N(sqrt(N)).

Code

Output

Explanation:

• In the above example, we can see that all the process is the same as in example 1 with the small changes in the isprime() function`.
• Instead of running for loop from 2 to number n, we are running the for loop from 2 to the sqrt(N). The small change in the code will reduce the time complexity from $O(N^2)$ to $O(N * sqrt(N))$.

Example 3: Display Prime Numbers from 1 to N

In this example, we will find the prime numbers between 1 to N, where N will be taken as an input from the user.

Approach: The approach of this problem is the same as Example 2. Instead of running a for loop from 1 to 100, we will run a loop from 1 to n, where n is an input taken from the user. To take input from the user, we will use the Scanner class.

Code

Output

Explanation:

The above example is the same as an example 2. The only difference is input. In the above example, we have taken n as input from the user, and we are running the loop from 1 to n.

Time Complexity: $O(N * sqrt(N))$ as discussed before.