How to Find Pythagorean Triplet in an Array?

Introduction

Pythagoras theorem is a theorem in geometry that says that in a right-angled triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides. Pythagorean triplet is a set of 3 numbers that satisfies the Pythagorean theorem. According to Pythagoras' theorem, in a right-angled triangle, the square of the hypotenuse equals the sum of squares of the other two sides. Pythagoras theorem has many real-life applications from architecture to navigation systems.

For example, if we know the height of the roof and the length to cover it then we can use Pythagoras theorem to find the diagonal length of the roof's slope.

Introduction to Pythagoras Theorem

Another example is the Pythagoras theorem can be used in two-dimensional navigation systems.

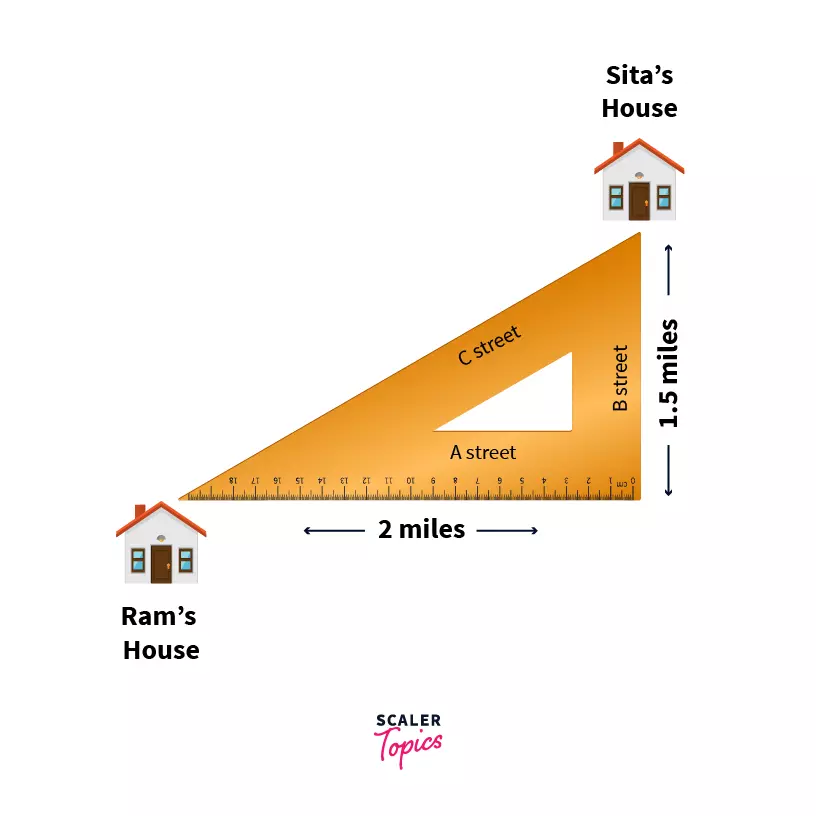
Suppose you are standing at a place and there is place A north of you at some distance and there is another place B east to you at some distance then using Pythagoras theorem to find the shortest distance between places A and B.

Pythagorean Triplets Example

Methods to Find Pythagorean Triplet in an Array

Naive Method

Steps:

Run a nested loop that will pick 3 elements from the array namely a, b, c.
Check if a, b, c follows pythagoras theorem.

Time Complexity: $O(n^3)$ since we are running nested loop with 3 levels.

Space Complexity: $O(1)$ since we are not using any extra space.

Using Sorting

Steps:

Square every number in the array.
Sort the array in ascending order.
Let's say we want to find a triplet (i,j,k) (where i,j,k are indices in the array) such that arr[i] = arr[j] + arr[k].
For finding the triplet (i,j,k) we will run a loop from the end of the array fixing i and then we will apply meet in the middle technique in the array from 0 to i - 1 to find the pair (j,k) such that arr[i] = arr[j] + arr[k].
If arr[j] + arr[k] = arr[i] then a triplet is found, else if arr[j] + arr[k] > arr[i] then decrement k i.e k- -, else increment j i.e j++.
If triplet is not found then decrement i i.e i- - and repeat step 5.

Time Complexity: $O(n^2)$ since we are running nested loop with 2 levels.

Space Complexity: $O(1)$ since we are not using any extra space.

Using Hashing

Steps :

Store every number of the array in the hash array.
Let's say we want 3 numbers namely a, b, c satisfying pythagoras theorem i.e $a^2 + b^2 = c^2$
For step 2, run a nested loop trying all possible combinations of a and b, then we will check for c in the hash array, if c exist then triplet exist otherwise not.

Time Complexity: $O(n^2)$ since we are running nested loop with 2 levels.

Space Complexity: $O(max1)$ where max1 is the maximum number in the array.

Using STL

Steps:

Store every number of the array in an unordered map.
Let's say we want 3 numbers namely a, b, c satisfying pythagoras theorem i.e $a^2 + b^2 = c^2$
For step 2, run a nested loop trying all possible combinations of a and b, then we will check for c in the map, if c exist then triplet exist otherwise not.

Time Complexity: $O(n^2)$ since we are running nested loop with 2 levels.

Space Complexity: $O(n)$ .

Using Set (A better hash-based approach)

Steps:

First square every array elements and then sort them in increasing order.
Run two loops where the outer loop starts from the last index of the array to the second index (0 based indexing is assumed) and the inner loop starts from outerLoopIndex – 1 to the start
Create a set to store the elements in between outerLoopIndex and innerLoopIndex.
Check if there is a number in the set which is equal to arr[outerLoopIndex] – arr[innerLoopIndex]. If yes, then return “True”.

Time Complexity: $O(n^2)$ since we are running nested loop with 2 levels.

Space Complexity: $O(n)$ .

Conclusion

In this article we learned :

Pythagoras theorem which says in a right angled triangle, square of the hypotenuse is equal to the sum of squares of the other two sides.
How to find pythagorean triplet in the given array using different approaches like naive approach, sorting, hashing, and STL.