Explain the Quick Sort Technique in C language

Types of sorting

In C language, there are five commonly used sorting techniques, each with its unique approach:

1. Bubble Sort (Exchange Sort)
2. Selection Sort
3. Insertion Sort (Linear Sort)
4. Quick Sort (Partition Exchange Sort)
5. Merge Sort (External Sort)

In this article we will discuss about working of Quick Sort algorithm.

What is Quick Sort in C?

• Quick Sort in C is a Sorting algorithm, which uses Divide and Conquer Approach to perform sorting.
• Quick Sort in C is the most efficient algorithm among all other sorting algorithms, as sorting can be done in O(n*logn) time.
• The Initial step of Quick Sort algorithm is to select the pivot element, and then rearrange the elements around the pivot element. A pivot can be any element in the array or a pivot can be first or last element of the array or it could either be the median of the array.

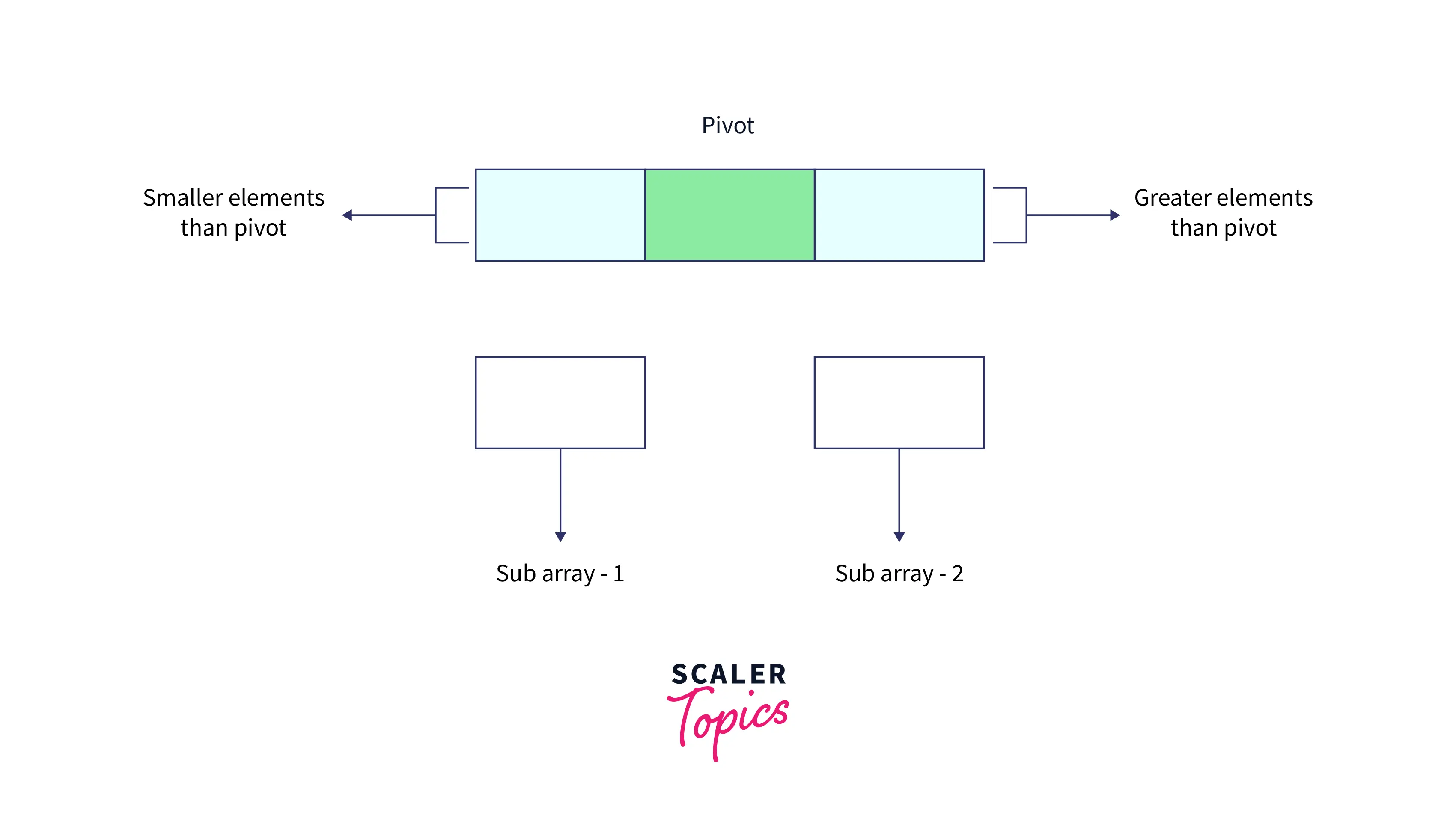
• After selecting the pivot element, we would rearrange the array elements and then split the array into two sub arrays such that all the sub array 1 contains array elements which are lesser than pivot while sub array 2 contains array elements greater than pivot.
• Interesting thing about the Quick Sort algorithm is that the chosen pivot element would be placed at the exact index position where it should be in sorted array because all elements to its left is less than pivot element and all elements to its right are greater than it.
• Each sub array is further divided until each sub array contains only single array element. Then we will combine all such sub arrays to form a single sorted array.
• For better understanding of Quick Sort algorithm, Assume this, your group of friends went for a trip and now its time to capture a group photo, to ensure that image looks good and to make everyone visible in the photograph, all of your friends must stand height wise, here Instead of photographer telling everyone to stand at a particular position by comparing every one’s height, all of your friends can stand at a position because everyone knows their own height. For example, the tallest guy knows were to stand and the medium guy knows where to stand. In a similar way each one of you friends can stand by comparing their own height with others.
• Similarly, In Quick Sort algorithm every array element arranges itself by comparing its value with others to sort the given array. So, pivot element would be placed exactly at its sorted position. Thereby, sub arrays are divided around the pivot element.

Quick Sort Algorithm in C

The execution of Quick Sort Program in C starts from the main function, before we actually call the quick sort function, we define the size of the array and array elements

Pivot: Pivot is an element which is selected by an algorithm to perform calculations

Step 1: Initial step in the algorithm is to select a Pivot element, Generally we have the flexibility to choose the pivot element as first element or last element or median element or any random element. For more efficiency, Last element of the array is picked as pivot, so let’s consider the last element as the pivot.

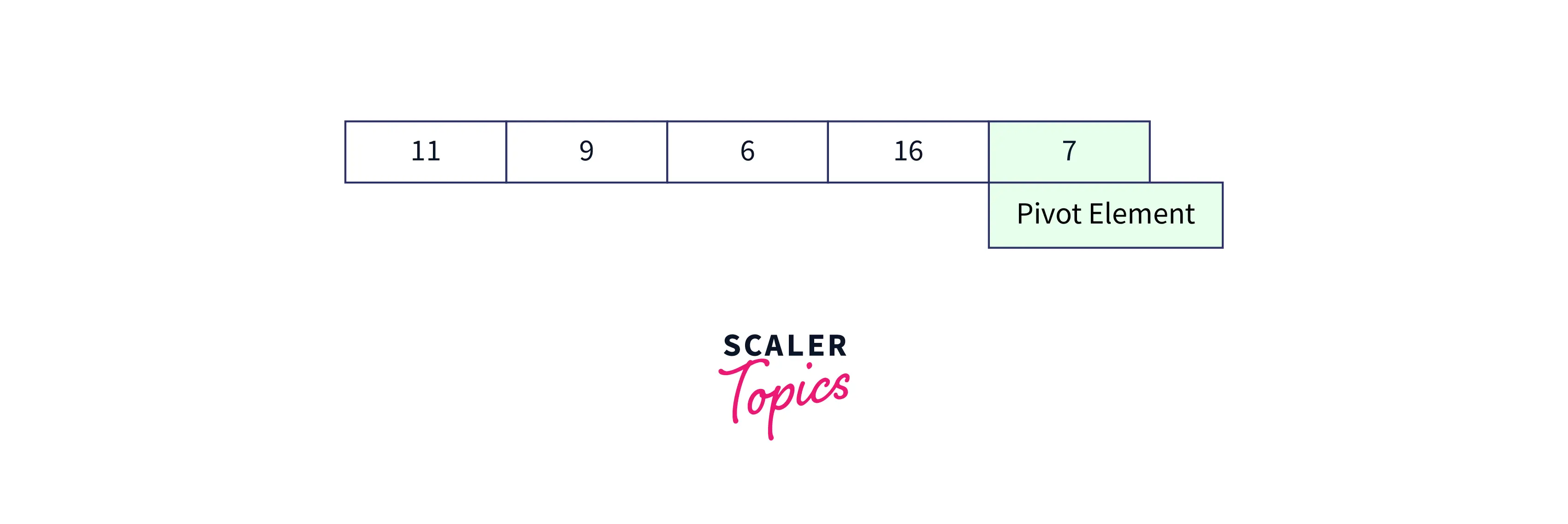
Step 2: In this step, we need to partition the array elements in such a way that elements smaller than pivot are placed to the left side of pivot while the elements greater than pivot are placed to the right side of the pivot. Please note that at this step elements need not be sorted. The array would look like the below image after rearranging.

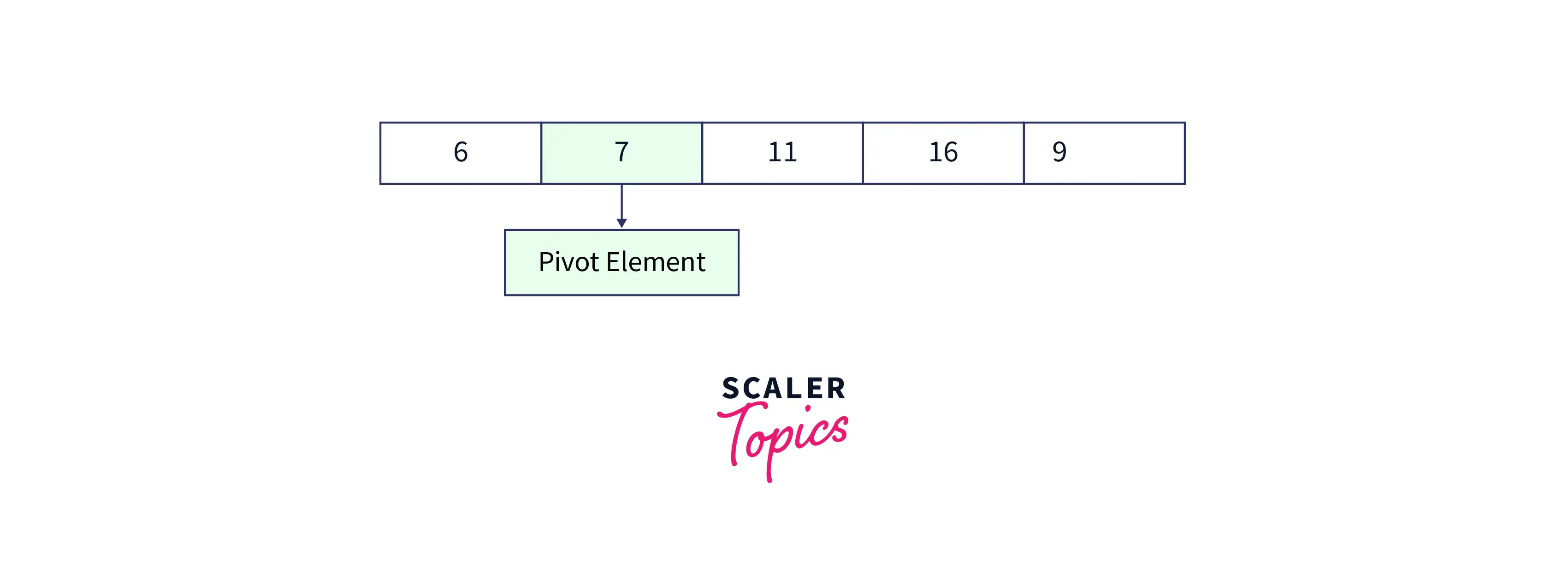
Now we have partition the array, let us understand the actual process of rearrangement:

• Let us take two variable i,j, Here i variable is used for swapping while j variable is used for iterating over array elements. Elements less than pivot are to be stored till ith position.
• Let us initialize 0th index as low and last index of the array as high, note that we will be traversing the array till high-1.

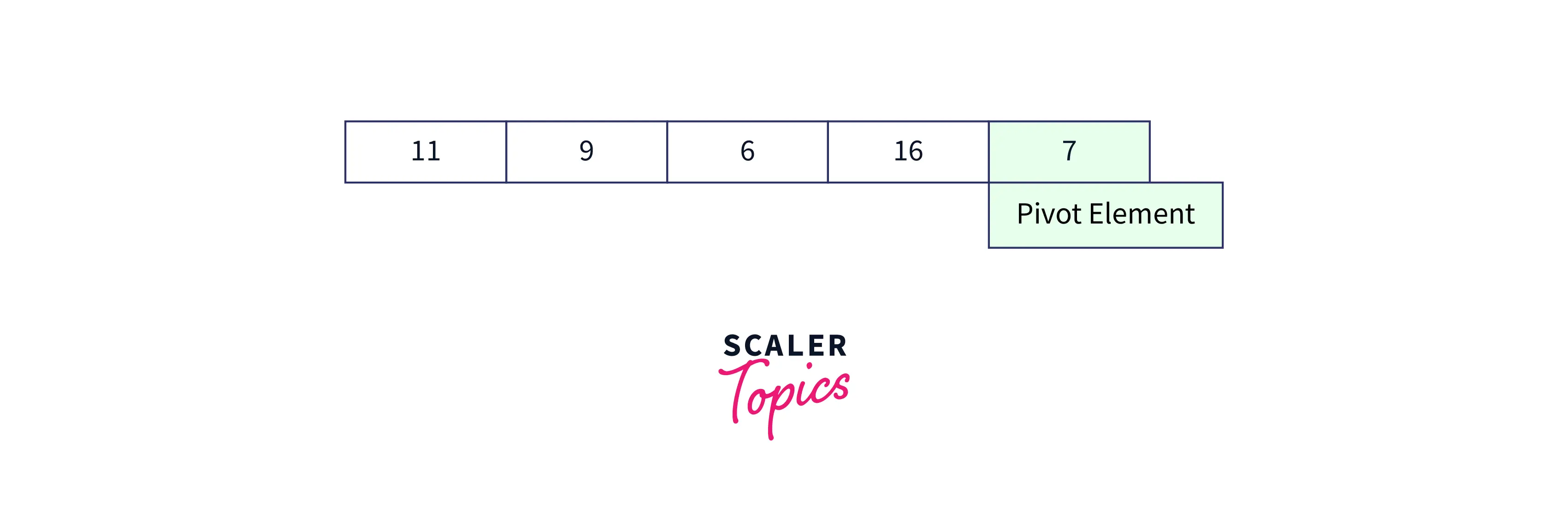
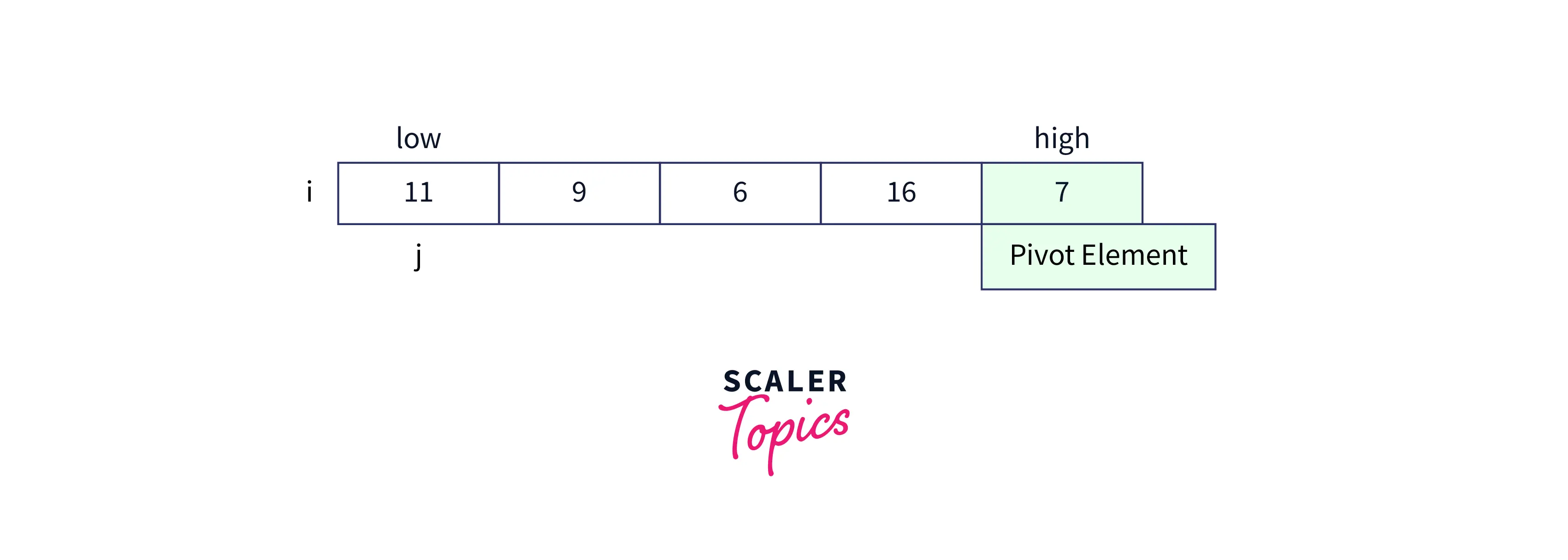
• Now, initialize the i,j variables as i=low-1, j=0.

• Compare the value at index j and pivot, if value at index j is less than pivot then increase the value of i and perform swap operation for i and j. As current jth index element 11 is not less than pivot element 7, we does not perform swap operation and increments the j value to move to next index element.

  

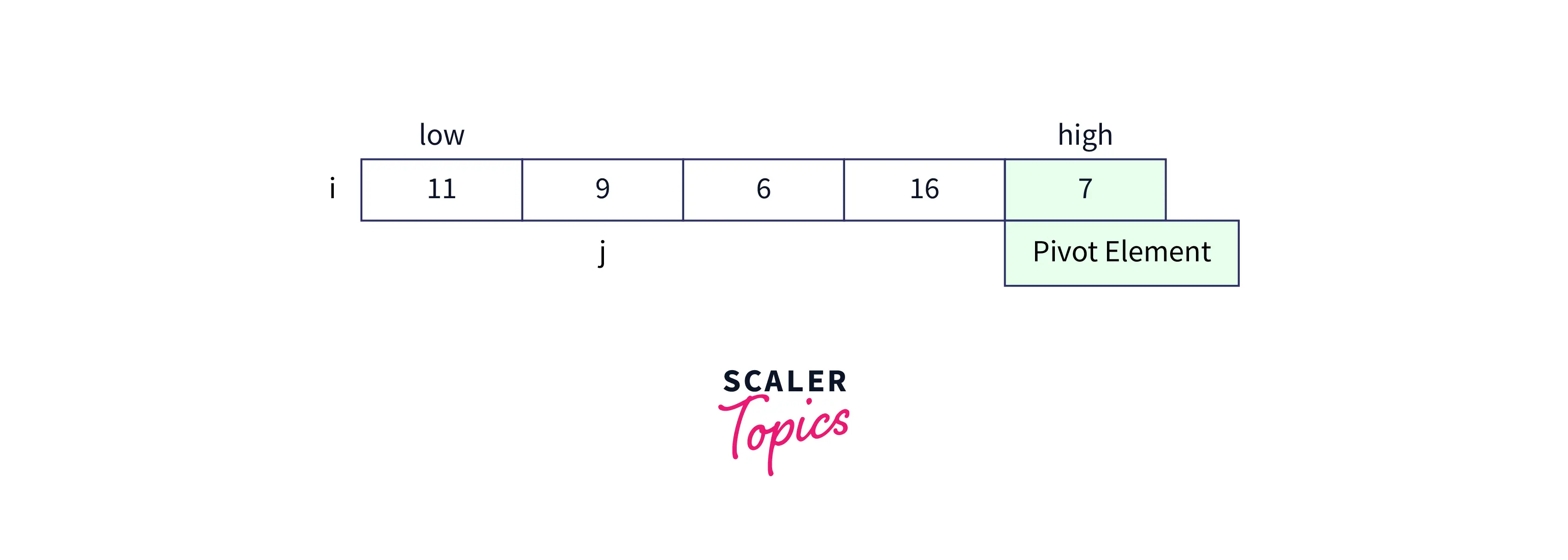
• Now again compare value at index j and value of pivot element, since 9 is not less than 7 we don’t perform any swap and simply increments the value of j to move to next index.

  

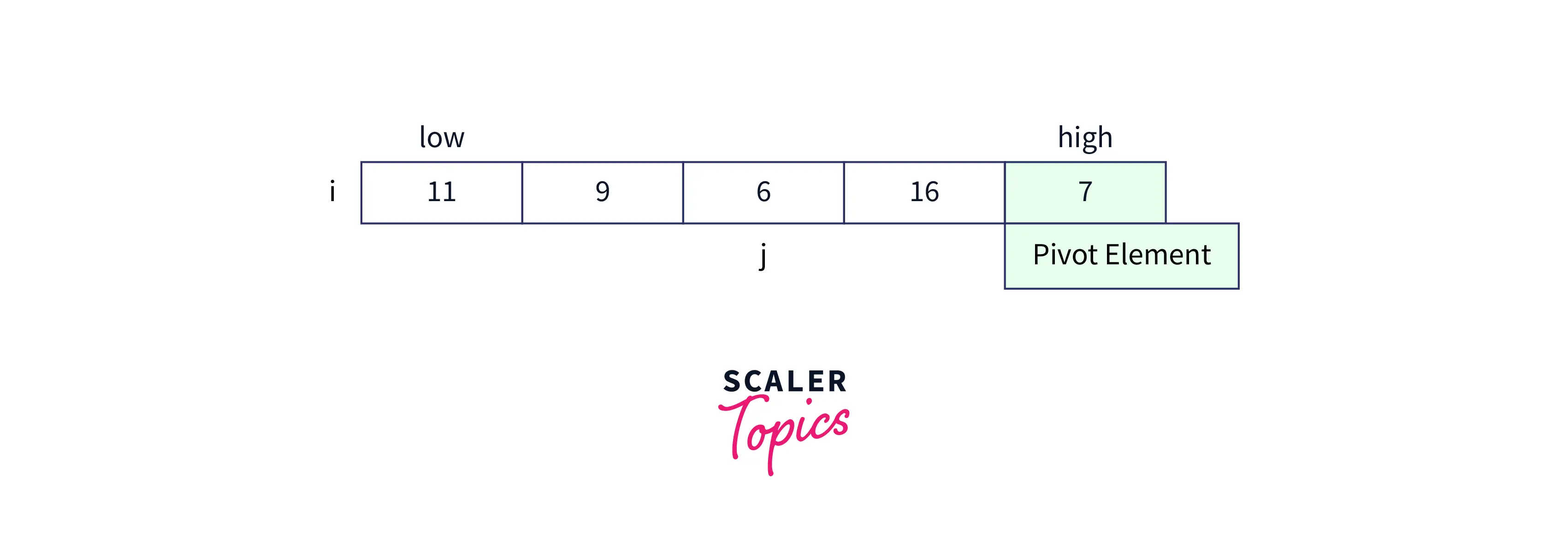
• Now value at jth index i.e 6 is less than value of pivot element 7. So, we perform swap operation, by increasing the ith index and perform swap between ith index and jth index.

fig: After performing swap operation array would look like the above image.

• Let us compare value at jth index with value at pivot element, since 16 is not less than 7 we do not perform any swap operation.

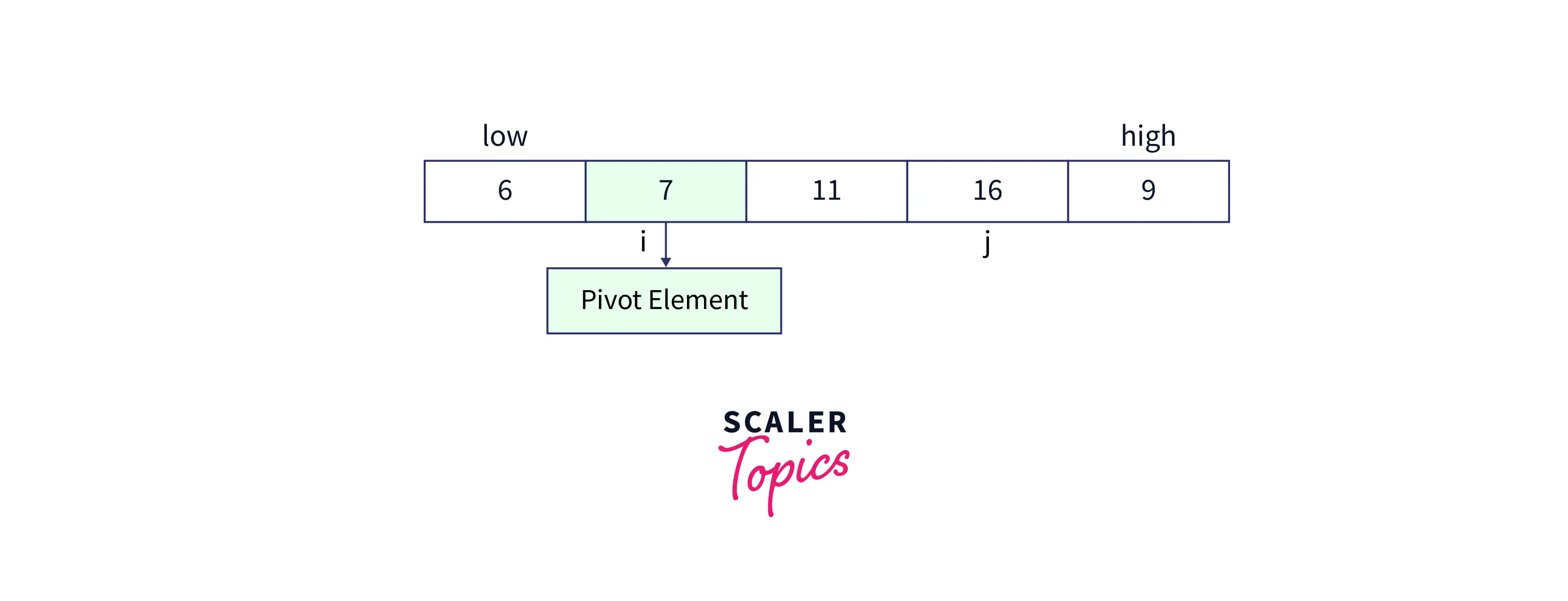
• Here comes our last step of the partition, now increment the value of i and swap ith index element with pivot element.

• Observe that all the element to left side of pivot are lesser than pivot while all the elements to right side of pivot are greater than pivot. This is the actual process of rearranging the elements around pivot. Kindly take a moment to visualize the process as it would be beneficial while writing the code for the Quick Sort Program in C.

Step 3: In this step, the entire array divides into two sub-arrays, i.e. sub-array-1 as elements before the pivot element and sub-array-2 as elements after the pivot element.

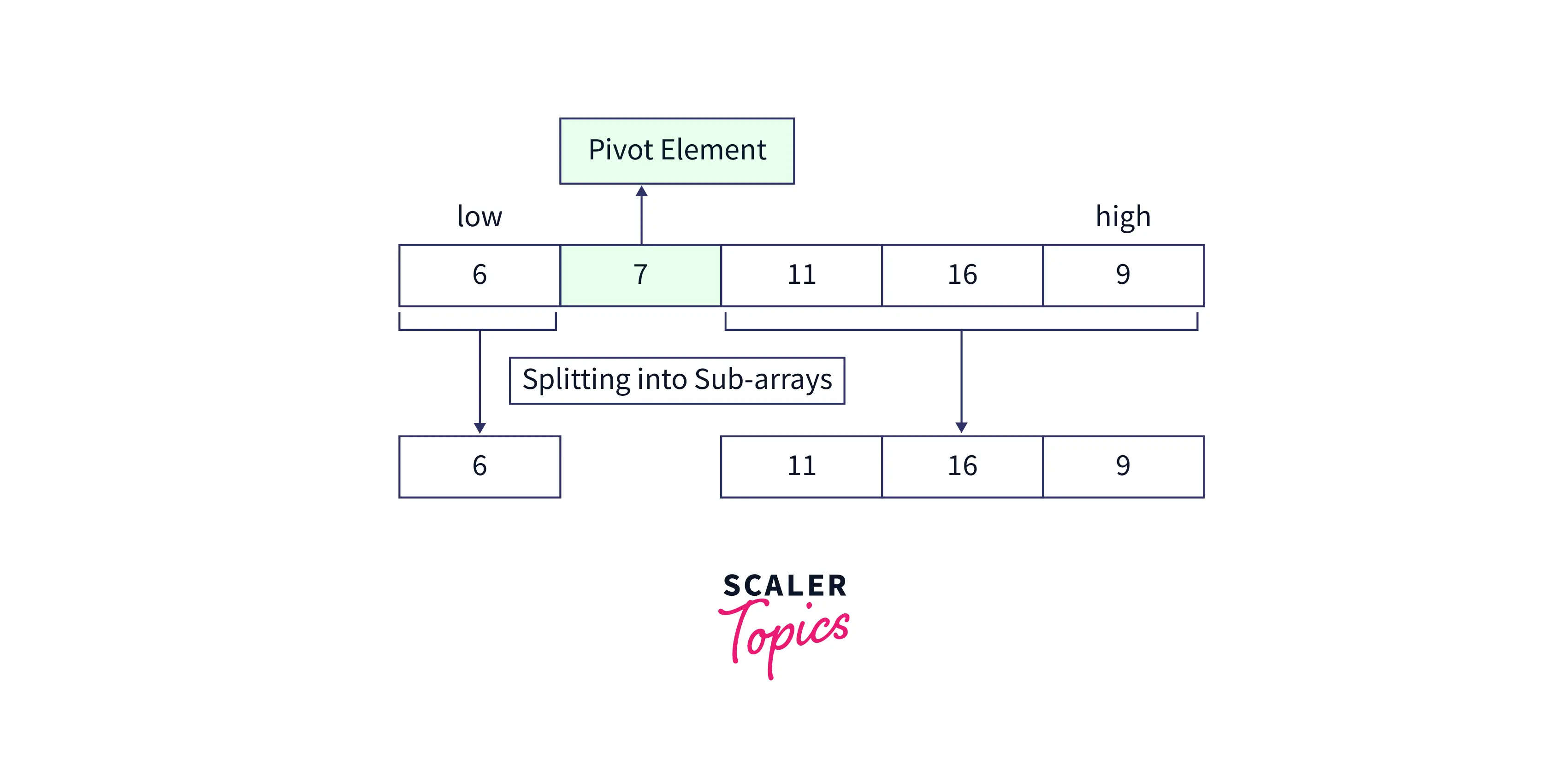
• I hope by this time, you might have gained a good understanding of the algorithm

Step 4: This step is very simple, repeat the above discussed steps for every sub array till both the whole array get sorted.

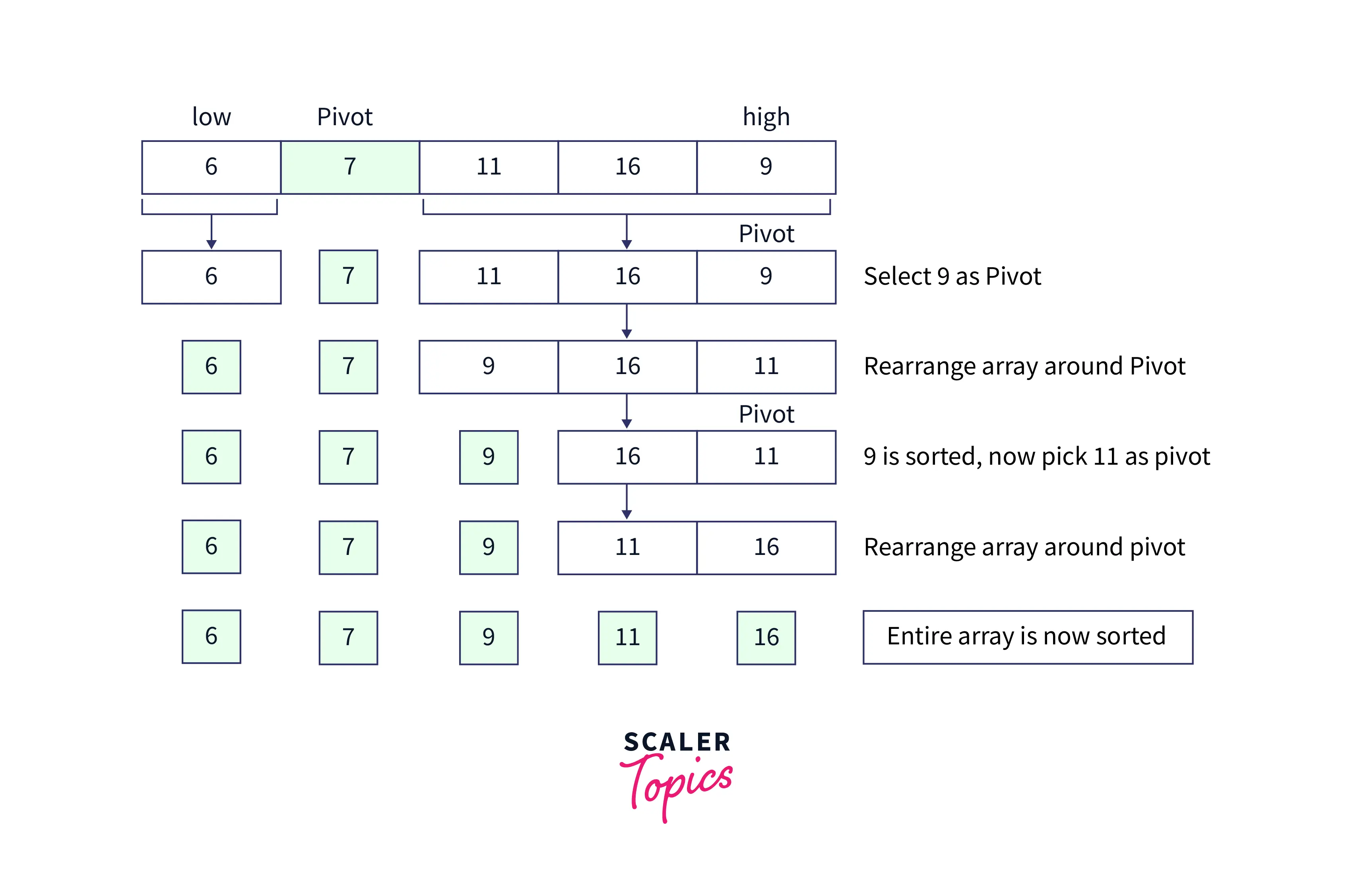As the sub arrays are now sorted this makes the entire array as a sorted array.

Pseudocodes for QuickSort Algorithm

Pseudocode Function for Partition Function

Partition function will divide the array according to the pivot and returned the correct index of the pivot element.

Pseudocode Function for Quick Sort Function

Complexity Analysis of Quick Sort Algorithm

A. Time Complexity

Best Case

In Quick Sort Program, if the position of the pivot element is in the middle of the array and if we perform partition in the middle of the array it leads to best case performance.

For an Instance, Let us consider an array of n elements we will divide(partition) this array from middle such that every partition contains at most n/2 elements, continue this partition until each subarray contains only one element.

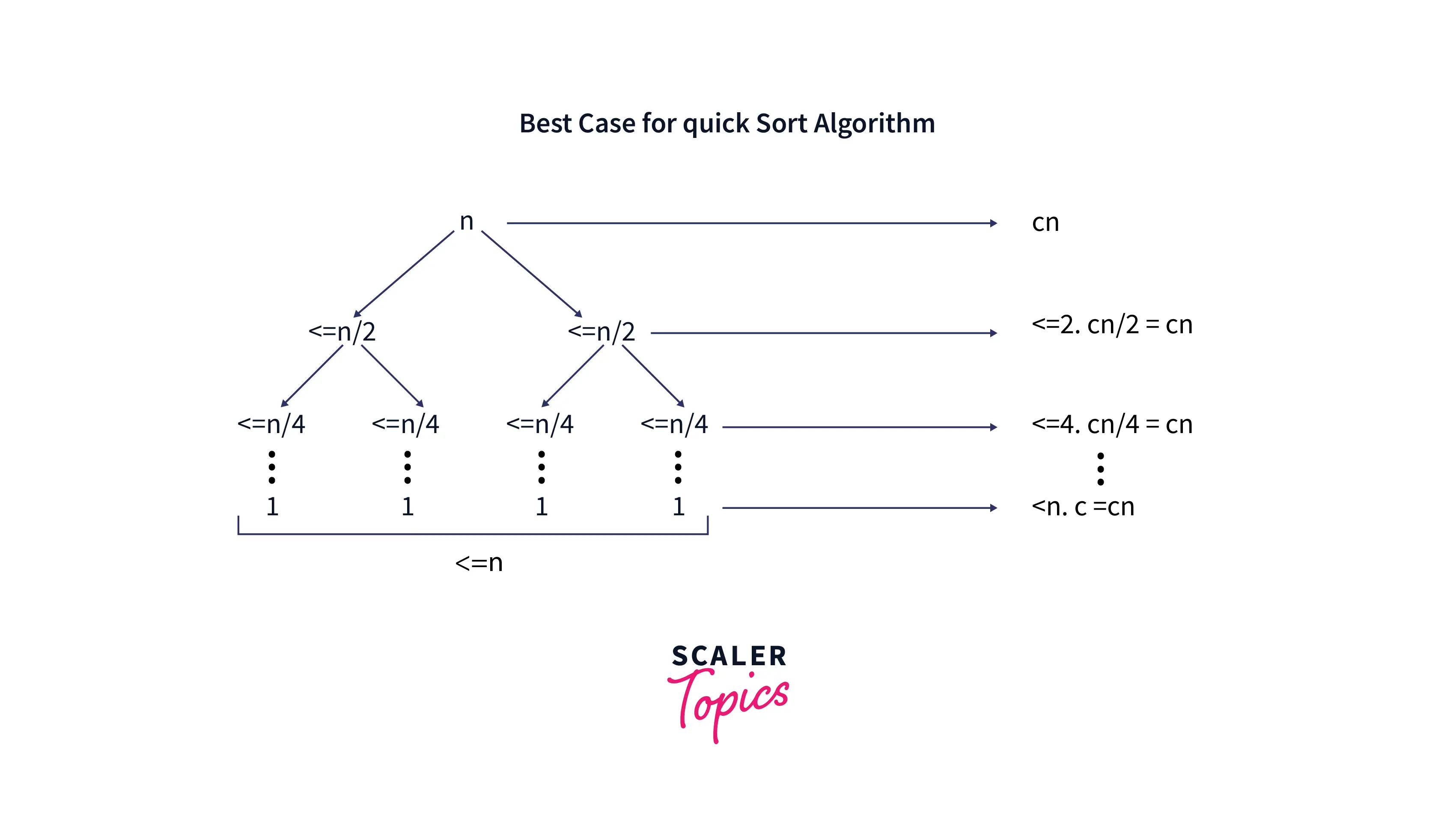
The above image is the representation of a binary tree, and height of a binary tree is equal to logn. Therefore the complexity of this part is O(logn). As we are iterating over the array for rearrangement of elements around the pivot element, the time complexity of partition() function would be O(n). So, we can conclude that O(nlogn) is the best case time complexity for Quick Sort algorithm.

Worst Case

In Quick Sort algorithm, if the partition is made in such a way that it is unbalanced, then Worst Case situation occurs. This unbalanced partition occurs if smallest or largest element is selected as the pivot.

In this situation, location of the pivot element would be at the end of array, so when partition is performed one sub array would be always empty while the other sub array would contain n-1 elements. So, for the first call, the two subarrays would contain 0 & n-1 elements respectively, while for second call subarrays would contain 0 & n-2 elements respectively, this process continues till only one element is left. So time complexity would be computed as sum of all complexities at each step. Number of steps are n and for every step O(n) time is required so time complexity of worst case is O(n*n). Refer the below image for the tree representation of this condition.

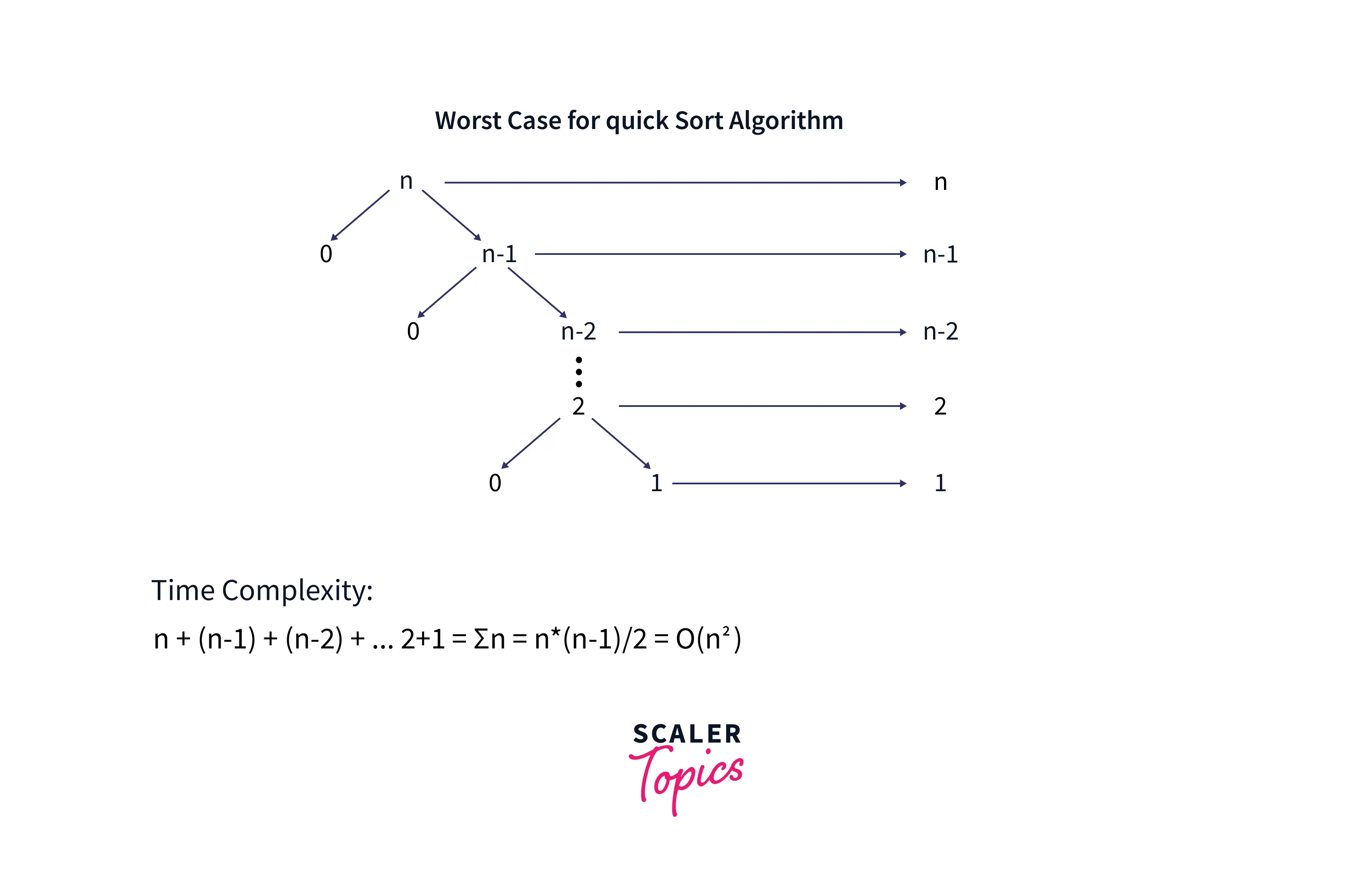
B. Space Complexity

In Quick Sort algorithm, the space occupied by Recursion Stack is used for calculating Space Complexity. In Worst Case Scenario, space complexity of Quick Sort algorithm in O(n) as n recursive calls will be made. Average space complexity for Quick Sort algorithm is O(log n).

Quick Sort Program in C using Iterative Mode

Output:

Let us understand the above Iterative implementation of Quick Sort Algorithm:

Flow of the program starts from the main function, we defined the array elements and called the quicksort function which creates a temporary array which will act as stack in this case by replacing the recursion stack. Then Quick Sort function uses a while loop to get the sorted index position of the partition element in the array, quicksort function itself calls the partition function to get the index of the sorted pivot element (partition function rearranges the array elements around the pivot). Quick Sort function uses this partition index and checks if there any elements to left side if yes then it adds the low, pi-1 indexes to the array so we could implement quick sort function in quick sort c program to that sub array later using this stack. Then it checks if there are any elements to the right side of the partition index, if yes, then it adds pi+1, high index to the array. Then by using these index values we go for another iteration in while loop until the entire array is sorted.

Quick Sort Program in C using recursion

Output:

Let us understand the above recursive implementation of Quick Sort Algorithm: The execution of the program starts from the main function, we declared the size of array and array elements. Now we are calling the quicksort function which in turn calls the partition function and rearranges the array elements around the pivot element and returns the partition index to the quicksort function, now quick sort function again calls itself to sort the elements which are lesser than pivot, after this quicksort function calls itself to sort the elements which are greater than pivot. In the above code we also have a swap function which is used by partition function to swap the jth index with ith index element. Finally in the main function we print the sorted array using a for loop.

When is Quick Sort Algorithm Used?

• Quick Sort Program in C is mostly used when stable sort is not required
  • Stable Sort: If the relative order of two equal elements is preserved after sorting, such an algorithm is called as stable sort.
• Quick Sort algorithm is mostly used where Time complexity matters.
• Quick Sort algorithm is mostly used where Space complexity matters.
• Quick Sort algorithm is used if the programming language is suitable for recursion.