Understanding Radial Basis Function (RBF) Neural Network

Radial basis function in machine learning neural networks are powerful tools in the realm of machine learning, offering unique capabilities for pattern recognition, function approximation, and classification tasks. Employing a distinct approach compared to traditional feedforward or recurrent neural networks, RBF networks utilize radial basis functions networks to transform input data into a higher-dimensional space for analysis and decision-making.
What is RBF in Machine Learning?
In machine learning the term "RBF" stands for "Radial Basis Function." It refers to a specific type of neural network architecture that utilizes radial basis functions networks (RBFs) as activation functions. RBF neural networks are distinct from traditional feedforward or recurrent neural networks due to their unique approach to processing input data and performing computations.
RBF Neural Network Structure
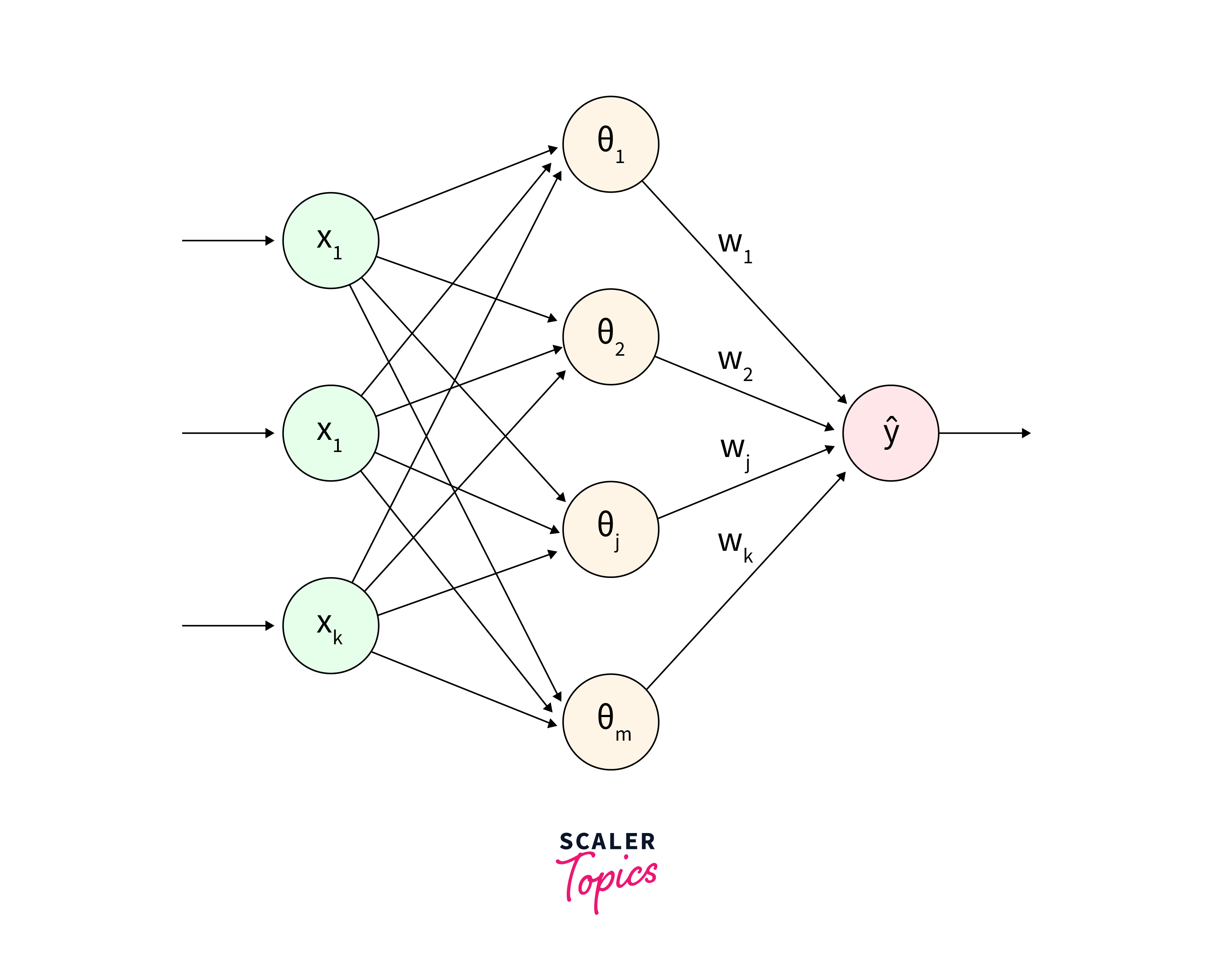
The Radial Basis Function neural network architecture diverges from conventional feedforward or recurrent neural networks, showcasing distinct layers with unique functionalities. The input layer receives and processes data, with each neuron representing a feature. Unlike traditional networks, the hidden layer of RBF networks is comprised of radial basis functions (RBFs), where each neuron corresponds to a function centered at specific points in the input space, offering a departure from densely interconnected layers. These RBFs, which can adopt various forms like Gaussian or Multiquadric functions, produce scalar outputs based on the distance between input data and the function's center, enabling the network to capture intricate data relationships.
In the output layer, which generates the final network output, neurons may represent class labels, continuous values, or categories depending on the task. The outputs of RBFs in the hidden layer are typically combined linearly through weighted sums, with weights learned during training. This weighted linear combination process allows for the integration of RBF outputs into the final network output, enhancing its ability to approximate functions, recognize patterns, and classify data effectively, especially in scenarios where traditional neural network architectures encounter challenges in generalization. The utilization of radial basis functions in the hidden layer thus empowers RBF networks to excel in various domains requiring the capture of radial symmetry or nonlinearity in input data, offering a powerful alternative for complex data analysis tasks.
Mathematical Understanding of Radial Basis Functions
Radial basis functions are mathematical functions whose value depends only on the distance from a specified center or origin. Commonly used radial basis functions include Gaussian, Multiquadric, and Inverse Multiquadric functions. Mathematically, a radial basis function can be represented as , where c is the center of the function and denotes the distance between the input vector x and the center.
How does RBF Work?
RBF neural networks operate by initially identifying suitable centers for radial basis functions, typically using clustering methods like k-means. These centers represent pivotal points in the input space. Once established, the network proceeds to learn the optimal weights for each radial basis function. These weights dictate the influence of each function in transforming the input data into a higher-dimensional space. This transformation facilitates the creation of linearly separable classes or functions. Subsequently, the transformed features are forwarded to the output layer, where they undergo a combination process. This layer synthesizes the transformed features to generate the final output of the network.
How to Train RBF Networks?
Training Radial Basis Function networks begins with center selection, where clustering algorithms like k-means are employed to identify pivotal points in the input space. These centers represent the foundation for radial basis functions. Subsequently, the network's weights are determined through techniques like least squares regression or gradient descent, aiming to minimize the disparity between the network's predictions and the actual output values. During this process, the network learns to adjust its weights iteratively to improve performance. The objective is to optimize the network's ability to accurately model the underlying relationships in the data.
Implementing RBF using Python
- Import necessary libraries such as NumPy for numerical computations and scikit-learn for clustering algorithms.
- Making the dataset
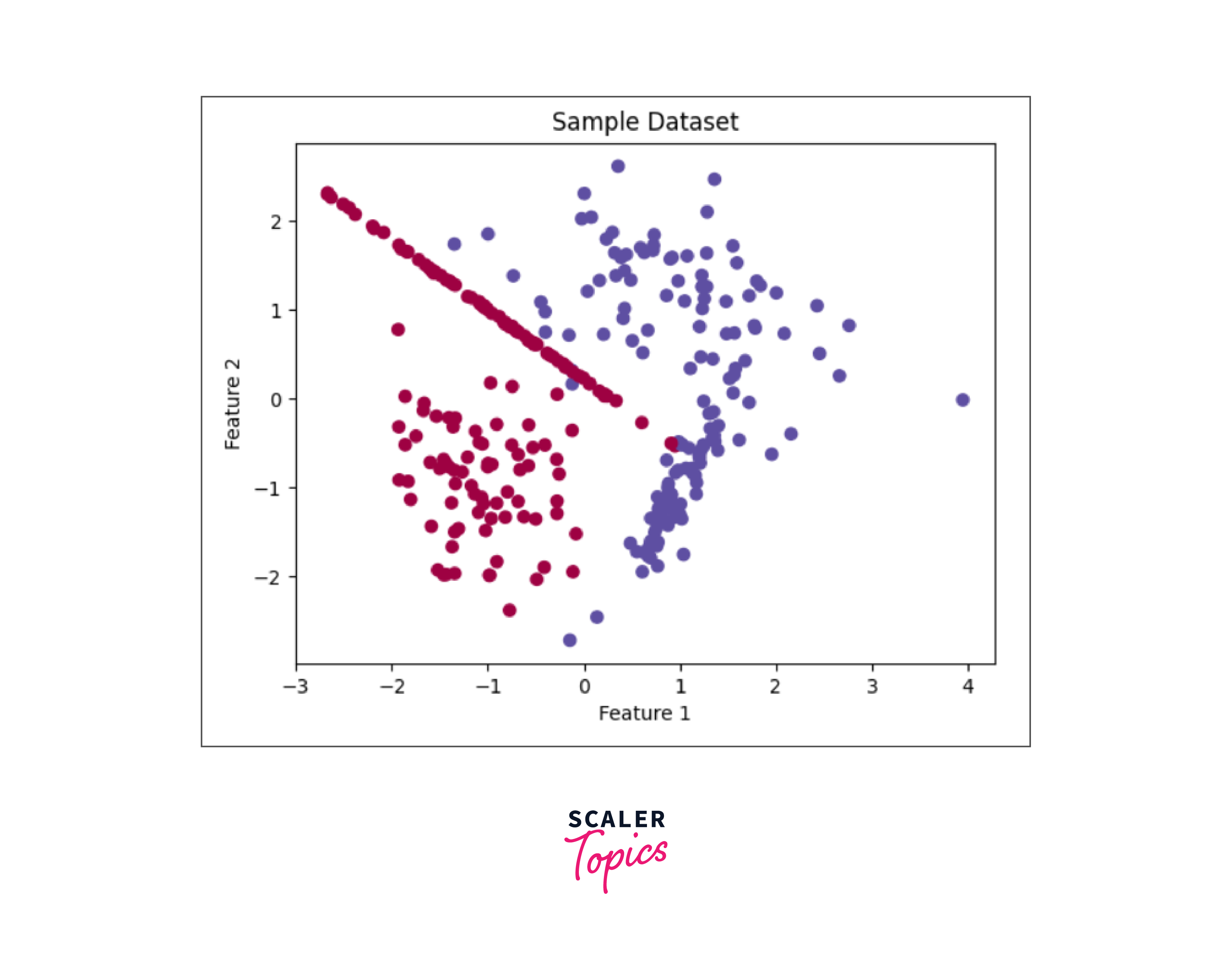
We will generate a synthetic dataset for our flower classification demonstration using scikit-learn. This dataset will consist of two features and two distinct classes. It will be utilized as both our training and testing data.
In the following code snippet, we create a dataset comprising 300 samples, 2 features, 2 classes, and 2 clusters per class. By specifying the random_state parameter, we ensure the reproducibility of our results.
Visualization of the dataset:
Output:
- Data preprocessing
Prior to constructing our RBFN (Radial Basis Function Network), it is essential to preprocess the data. Standardization, also known as feature scaling, is a critical step in this process. It ensures that all features are on the same scale, which is necessary for the effective operation of RBFNs.
Utilizing the StandardScaler module from scikit-learn, we standardize our data.
- Initializing the RBF
Now, we reach the core of our RBFN (Radial Basis Function Network) implementation: the radial basis functions.
For this example, we'll employ Gaussian radial basis functions. The Gaussian RBF is defined as follows:
In this equation:
- represents the output of the radial basis function for input .
- is the center of the radial basis function.
- is the width parameter of the Gaussian function, which determines the spread of the function around its center.
- denotes the squared Euclidean distance between the input and the center .
- denotes the exponential function, which raises Euler's number to the power of the argument.
Here’s the Gaussian RBF in Python:
- Selecting the centers and width for RBF
Determining the suitable RBF centers and width is pivotal for the effectiveness of your RBFN (Radial Basis Function Network) model. The selection of centers should be made judiciously considering the distribution of your data, while the width needs to be configured to regulate the impact of each RBF.
Now, let's proceed to randomly choose the centers for our RBFs and establish a default width:
In this instance, we opt to designate 10 random data points as our RBF centers. Initially, the width is fixed at 1.0.
- Building the Radial Basis Function
Now that our data has been preprocessed and our RBFs defined, we can proceed to construct our Radial Basis Function Network (RBFN). Our network will be composed of two layers:
- The first layer comprises the Gaussian RBFs.
- The second layer is a linear layer responsible for amalgamating the outputs of the RBFs.
In the rbf_layer function, we calculate the outputs of our Gaussian RBFs. Subsequently, the rbfn_predict function utilizes these RBF outputs along with weights to make predictions for the outcome.
- Training the model
Training an RBFN entails discovering the optimal weights that minimize the disparity between the predicted values and the actual target values. In our demonstration, we'll employ sci-kit-learn's train_test_split function to generate training and testing sets. Subsequently, we'll utilize linear regression to ascertain the optimal weights.
Output:
- Visualizing the results
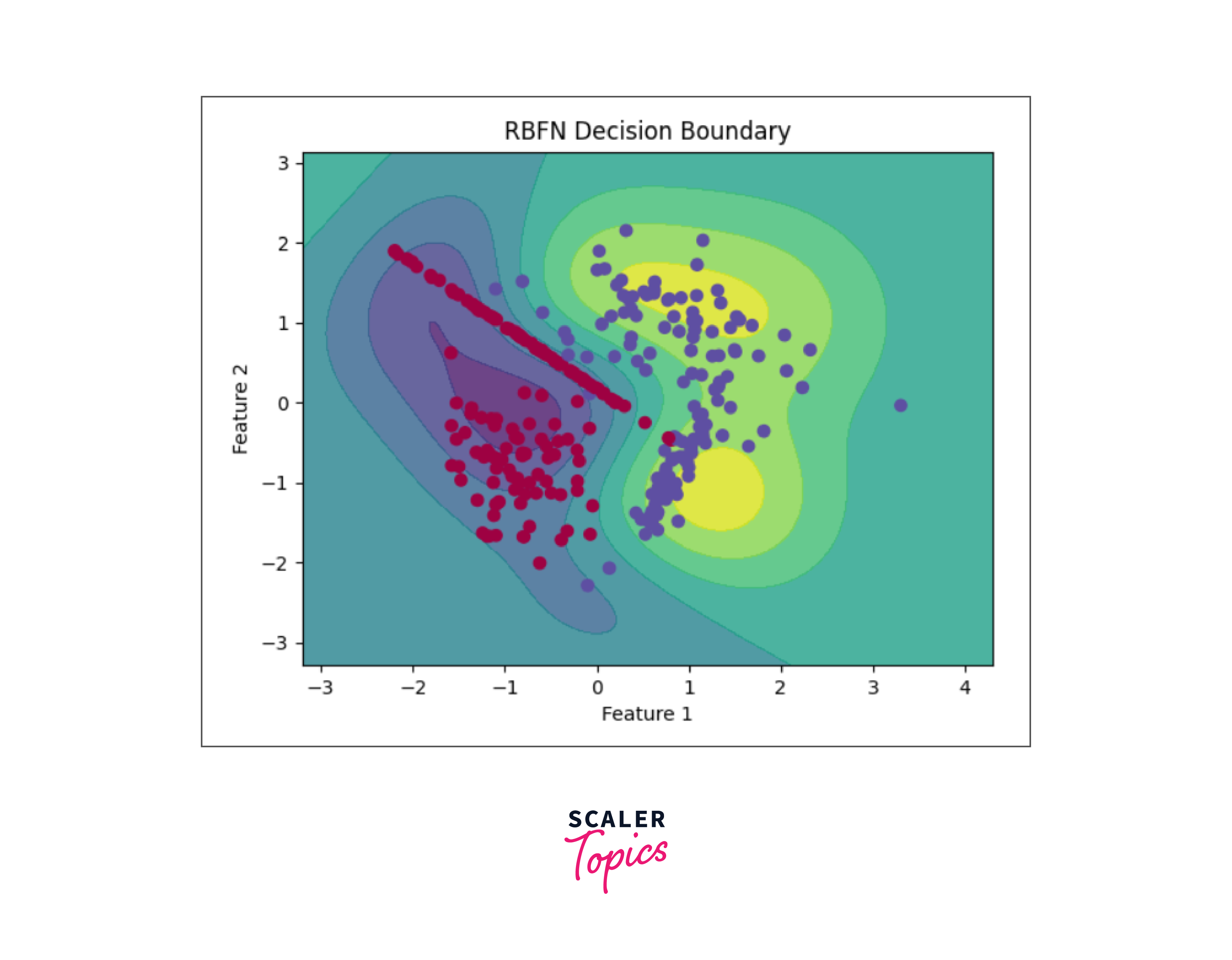
Conclusion
- Radial basis function (RBF) neural networks provide a distinct method for addressing intricate machine learning tasks, employing radial basis functions to process input data.
- Mastery of the structure, mathematical underpinnings, and training methodologies of RBF networks empowers practitioners to harness their capabilities effectively across diverse applications.
- RBF networks epitomize a captivating fusion of mathematical principles and pragmatic implementation within the realm of machine learning.
- Offering an alternative paradigm to conventional neural network architectures, RBF networks excel in handling nonlinear relationships and high-dimensional datasets.
