Regression Analysis in R

What is Regression Analysis in R?

As discussed earlier, regression analysis is a statistical technique used to examine the relationship between one or more independent variables (also known as predictors, features, or input variables) and a dependent variable (also known as the outcome or response variable).

The goal of regression analysis is to understand how changes in the independent variables are associated with changes in the dependent variable and to make predictions or inferences based on this relationship.

Regression analysis is immensely valuable in the field of healthcare to understand the relationship between various factors and patient outcomes. Consider a medical researcher investigating the effectiveness of a new drug in lowering blood pressure. They collect data from a sample of patients, recording variables such as age, weight, dosage of the drug, and initial blood pressure levels.

By applying regression analysis, the researcher can determine how each of these factors contributes to the reduction in blood pressure. This analysis not only provides insights into the drug's effectiveness but also identifies which patient characteristics or dosages might yield the best results.

Types of Regression Analysis in R

Linear Regression

Linear regression is a statistical technique that facilitates the analysis of relationships between a dependent variable and one or more independent variables. This method involves fitting a straight line to observed data points in a way that minimizes the difference between actual and predicted values. By using a linear equation, the goal is to capture the underlying trend between variables and make predictions based on this trend.

In its simplest form, known as simple linear regression, the relationship between the dependent variable (y) and the independent variable (x) is expressed as:

Where:

• y represents the dependent variable, which is the quantity being predicted.
• x represents the independent variable, acting as the predictor.
• β₀ is the intercept, denoting the value of y when x is zero.
• β₁ is the slope, indicating the rate of change in y for each unit change in x.
• ε denotes the error term, encompassing unexplained variations in y.

• Implementation of Linear Regression in R
  Output
  • Load Libraries:
    We start by loading the required libraries. We load the ggplot2 library for data visualization and the dplyr library for data manipulation.
  • Load Data:
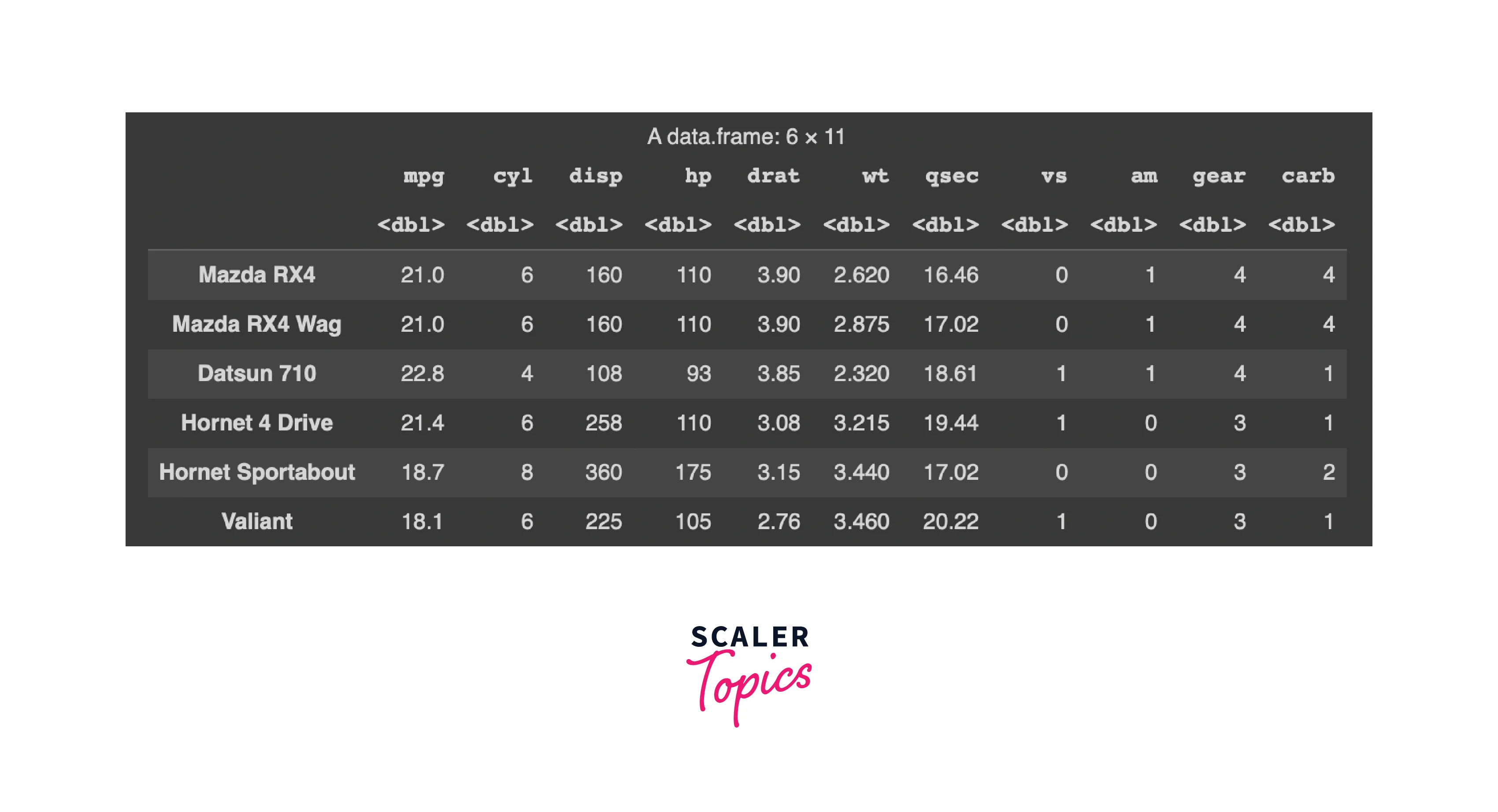
    We load a built-in dataset called mtcars. This dataset contains information about various car models, including attributes like miles per gallon (mpg), weight (wt), horsepower (hp), and more.
  • Explore Data:
    We use the head() function to display the first few rows of the mtcars dataset. This allows us to quickly inspect the structure of the data.
    Output

  • Create Linear Regression Model:
    We create a linear regression model using the lm() function. In this case, we're trying to predict the mpg (miles per gallon) of cars based on the wt (weight) attribute. The formula mpg ~ wt specifies this relationship.
  • Print Model Summary:
    We use the summary() function to display a summary of the linear regression model. The summary includes information about the coefficients, their significance (p-values), R-squared value, and more. This summary helps us understand the model's performance and the significance of the predictor (wt) in predicting the response variable (mpg).
    Output
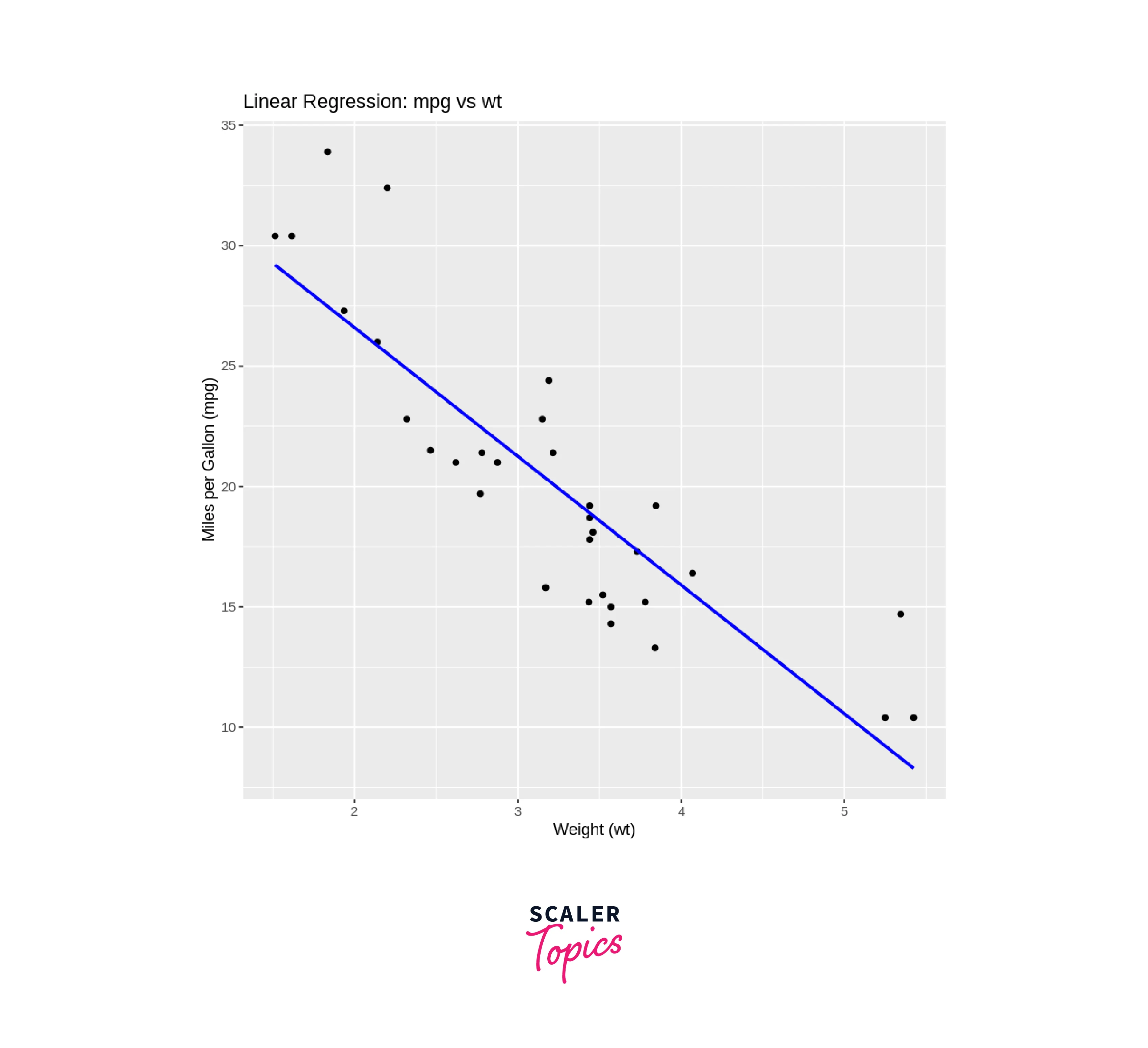
  • Visualize Data:
    We use the ggplot2 package to create a scatter plot of the data. We use ggplot() to initialize the plot and aes() to specify the aesthetics (variables) for the plot. We set x = wt and y = mpg to indicate that we're plotting the weight (wt) on the x-axis and miles per gallon (mpg) on the y-axis.
  • geom_point():
    This adds the actual data points to the plot as individual points.
  • geom_smooth(method = "lm", se = FALSE, color = "blue"):
    This adds a linear regression line to the plot using the method = "lm" argument, indicating that we want to use linear regression to fit the line. The se = FALSE argument removes the confidence interval shading around the line. We set the line color to blue using the color argument.
  • labs(...):
    This function is used to add labels to the plot, including the title and axis labels.
  The output will include the model summary and a scatter plot with the data points and the fitted linear regression line. This example provides a basic overview of how to perform linear regression in R, from loading libraries and data to creating the model, printing the model summary, and visualizing the results. In real-world scenarios, you may need to handle more complex datasets, perform feature engineering, and thoroughly evaluate the model's performance.

Logistic Regression

Logistic regression serves as a statistical technique employed in scenarios involving binary classification objectives. The objective here is to forecast whether an observation pertains to either of two potential categories. Despite its nomenclature, logistic regression doesn't forecast a linear correlation in the manner linear regression does. Instead, it frames the likelihood of an instance affiliating with a specific class.

In binary logistic regression, the probability p of an event occurring (e.g., a positive class) is modelled using the logistic function, also known as the sigmoid function:

Where:

• p is the predicted probability of an event.
• x is the independent variable.
• β₀ is the intercept.
• β₁ is the coefficient associated with the independent variable.

The logistic function "squashes" the linear combination of the intercept and coefficient into a value between $0$ and $1$, effectively representing the probability of the event occurring. If p is greater than $0.5$, the prediction is assigned to the positive class; otherwise, it's assigned to the negative class.

• Implementation of Logistic Regression in R

  • Load Libraries:
    We start by loading the required libraries. We load the ggplot2 library for data visualization and the dplyr library for data manipulation.

  • Load Data:
    We load a built-in dataset called mtcars. This dataset contains information about various car models, including attributes like miles per gallon (mpg), weight (wt), horsepower (hp), and more.

  • Explore Data:
    We use the head() function to display the first few rows of the mtcars dataset. This allows us to quickly inspect the structure of the data.

    Output

  • Create Logistic Regression Model:
    We create a logistic regression model using the glm() function. In this case, we're trying to predict the vs (categorical variable indicating engine type) of cars based on the wt (weight) attribute. The formula vs ~ wt specifies this relationship. We also set the family argument to "binomial" to indicate that this is a logistic regression.

  • Print Model Summary:
    We use the summary() function to display a summary of the logistic regression model. The summary includes information about the coefficients, their significance (p-values), deviance statistics, and more. This summary helps us understand the model's performance and the significance of the predictor (wt) in predicting the response variable (vs).

    Output

    

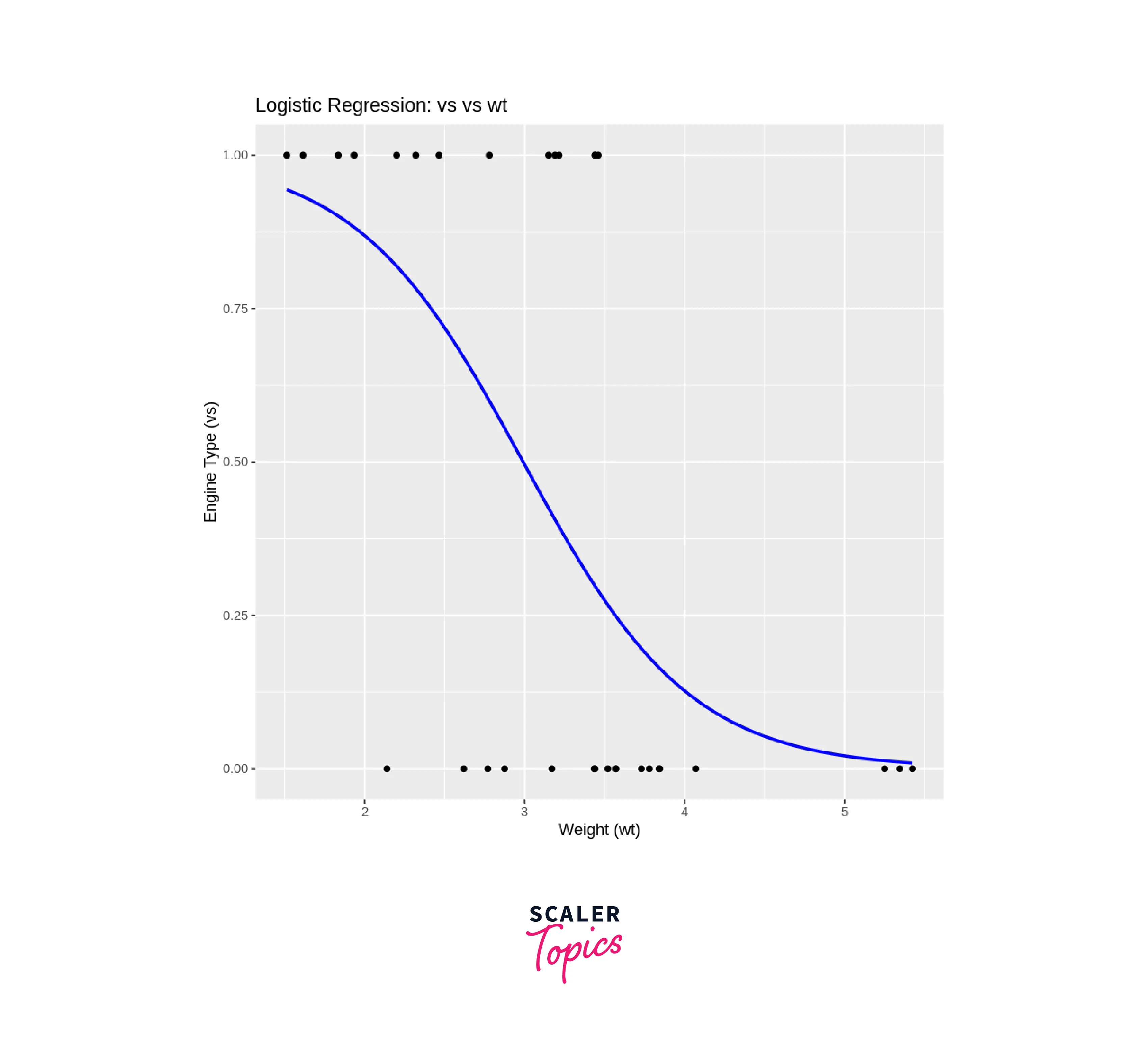
  • Visualize Data:
    We use the ggplot2 package to create a scatter plot of the data. We use ggplot() to initialize the plot and aes() to specify the aesthetics (variables) for the plot. We set x = wt and y = vs to indicate that we're plotting the weight (wt) on the x-axis and the engine type (vs) on the y-axis.

  • geom_point():
    This adds the actual data points to the plot as individual points.

  • geom_smooth(method = "glm", method.args = list(family = "binomial"), se = FALSE, color = "blue"):
    This adds a logistic curve to the plot using the method = "glm" argument, indicating that we want to use logistic regression to fit the curve. The method.args argument is used to pass additional arguments to the glm() function, including the family argument set to "binomial". The se = FALSE argument removes the confidence interval shading around the curve. We set the curve color to blue using the color argument.

  • labs(...):
    This function is used to add labels to the plot, including the title and axis labels.

  The output will include the model summary and a scatter plot with the data points and the fitted logistic curve. This example provides a basic overview of how to perform logistic regression in R, from loading libraries and data to creating the model, printing the model summary, and visualizing the results. In real-world scenarios, you may need to handle more complex datasets, perform feature engineering, and thoroughly evaluate the model's performance.