What is RSA Algorithm?

Before moving forward with the algorithm, let’s get a refresher on asymmetric encryption since it verifies digital signatures according to asymmetric cryptography architecture

What Is Asymmetric Encryption?

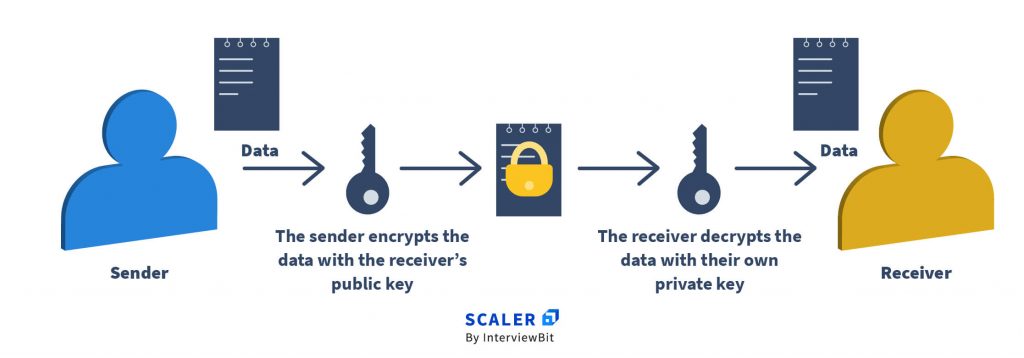
In Asymmetric Encryption algorithms, you use two different keys, one for encryption and the other for decryption. The key used for encryption is the public key, and the key used for decryption is the private key. But, of course, both the keys must belong to the receiver.

An example of asymmetric cryptography:

1. A client (for example browser) sends its public key to the server and requests some data.
2. The server encrypts the data using the client’s public key and sends the encrypted data.
3. The client receives this data and decrypts it.

What Are Digital Signatures?

Digital signatures serve the purpose of authentication and verification of documents and files. This is crucial to prevent tampering during official papers’ transmission and prevent digital manipulation or forgery. When dealing with digital signatures the private key is used to encrypt the signature, and the public key is used to decrypt it.

There are two industry-standard ways to implement the above methodology. They are:

1. RSA Algorithm
2. DSA Algorithm

We will discuss about RSA Algorithm in following article.

Mechanism behind the RSA algorithm

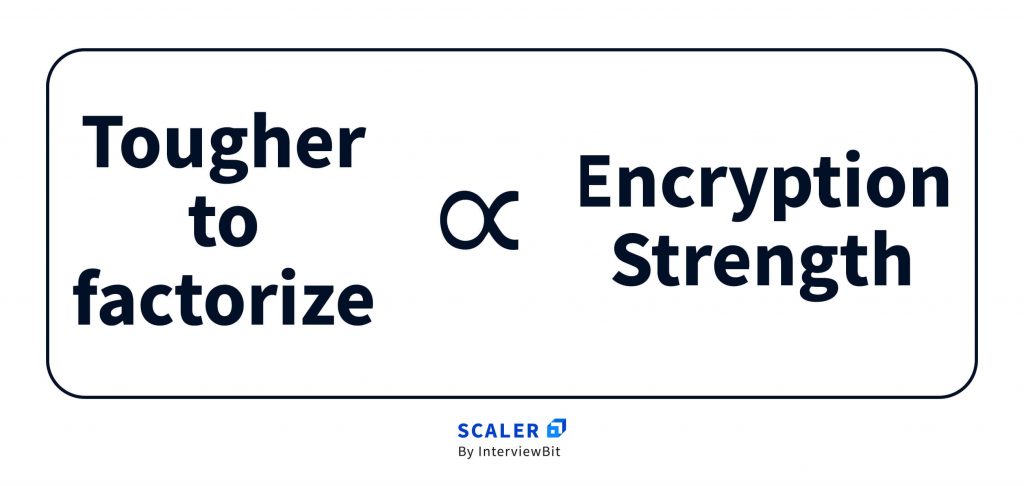
The idea of RSA is based on the fact that it is difficult to factorize a large integer. The public key consists of two numbers where one number is a multiplication of two large prime numbers. And private key is also derived from the same two prime numbers. So if somebody can factorize the large number, the private key is compromised. Therefore encryption strength totally lies on the key size and if we double or triple the key size, the strength of encryption increases exponentially. RSA keys can be typically 1024 or 2048 bits long, but experts believe that 1024-bit keys could be broken in the near future. But till now it seems to be an infeasible task.

Let’s take an example here.

How about two exotic-looking aliens from the RSALand talking to each other.

So, here’s how it goes.

You come across two exotic-looking aliens, from the planet called RSALand, having a great time talking to each other.

And just like an average conversation in the world, you find there’s a talkative alien (aka the Sender) & a quieter alien (aka the Receiver)

They are using the RSA Algorithm to maintain secrecy in their conversations (smart aliens)

They implement the RSA Algorithm using shiny balls of light. Cool enough.

And no my friends, these light balls don’t come in black (sorry, Batman)

They come in blue, pink, golden & green.

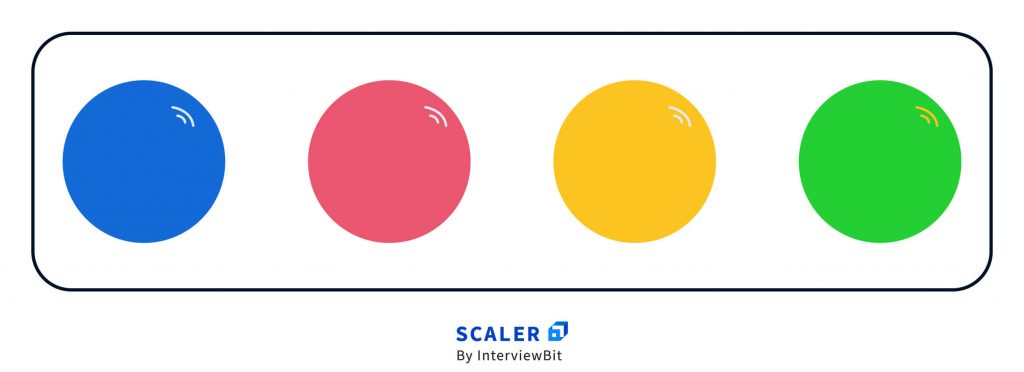
Every shiny ball of light represents one component of the RSA Algorithm.

The Receiver maintains Public-Private Key pair

1. Blue ball is the Receiver’s Public Key
2. Golden ball is the Receiver’s Private Key

The Sender encrypts their Original Message using Receiver’s Public Key

Pink ball is the encrypted message.

The Receiver decrypts the encrypted message using its Private Key

The decrypted message is simply the Sender’s Original Message.

Green ball is the decrypted message.

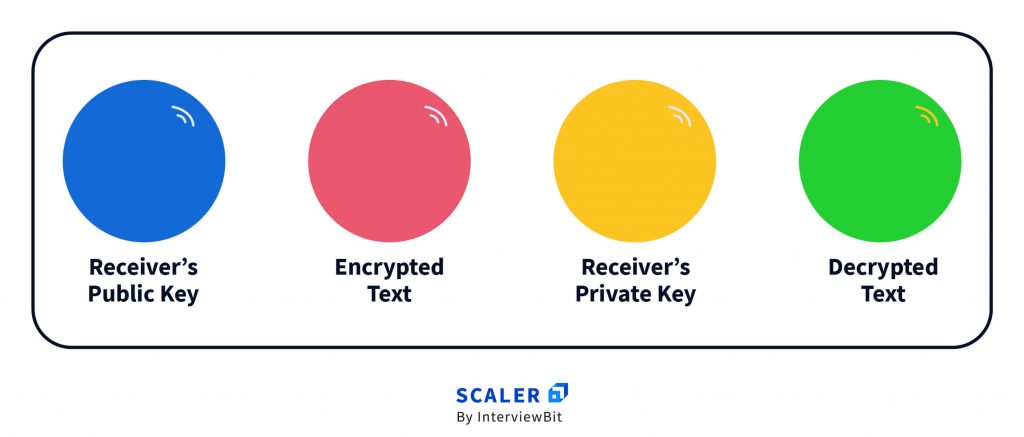
Here’s a quick snapshot of how their conversation plays out.

a. The Receiver alien creates a shiny blue light ball & throws it to the Sender

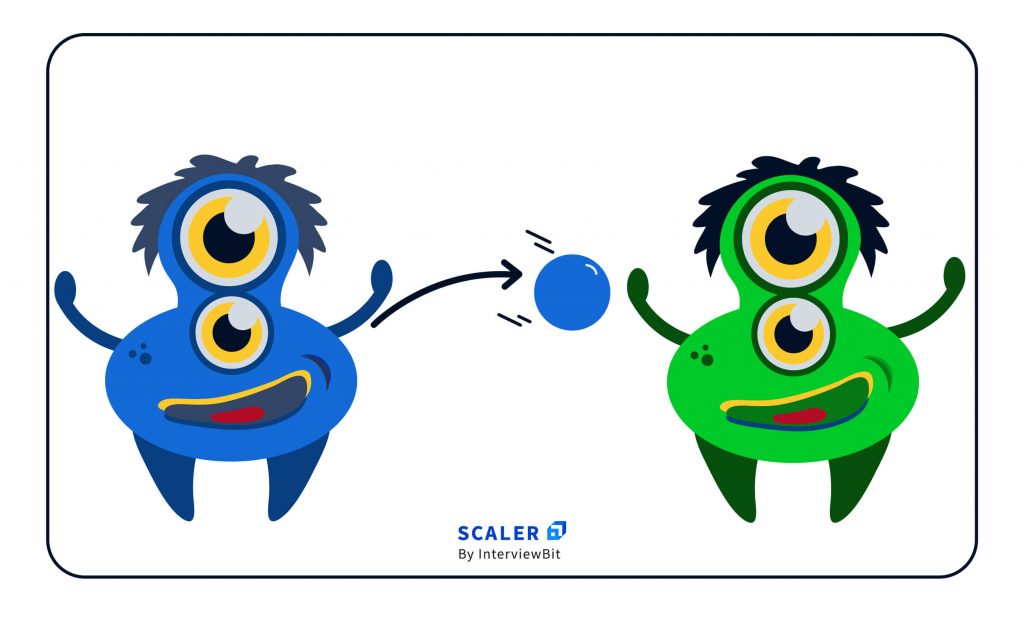
b. The Sender alien catches the blue light ball.

The sorcerous Sender changes the blue ball to a shiny pink ball & throws it back to the Receiver

c. The Receiver alien, like a pro he is, catches the thrown pink light ball.

Using his personal golden light ball, he fuses the pink & golden balls to get a dazzling green one.

Alright folks, now back to the real world.

• We select two large primes numbers p & q. Adequate care is taken to ensure that the two selected primes p & q are big & hard enough for anyone to figure.

  Quick fact folks! The selected primes can be anywhere from 1024 bits to 2048 bits long.

  That simply implies the maximum value of a selected prime can be as huge as 22048 -1!

  Note: We select numbers that are primes & preferably huge in value simply to make factorization tougher.

Remember, the tougher the factorization – the more secure is the encryption.

• n is calculated next, as

$n = p * q$

• Totient function (denoted by ϕ(n)) value is next to be calculated.

But wait. What’s even a totient function?

Totient function (or Euler’s totient function) for a given value s is simply the number of positive integers that are relatively prime to s.

If s is a prime number, the value of

$ϕ(s)$ is simply (s – 1)

Additionally, if two numbers c & d are relatively prime – then the value of totient function ϕ(c * d) evaluates to (c – 1) * (d – 1)

In this step of the RSA Algorithm, we calculate the value of

ϕ(n) = ϕ(p * q) which is simply (p – 1) * ( q – 1)

Note: Two primes are relatively prime to each other

Thus,

ϕ(n) = (p – 1) * (q – 1)

• An integer value e is selected such that

e is coprime to ϕ(n) &

$1 < e < ϕ(n)$ (the value of e lies between 1 and ϕ(n))

• An integer value d is calculated such that

$e * d = 1 mod ϕ(n)$ or

$d = (1 / e) mod ϕ(n)$

Generating Public Key

The pair of numbers (n, e) makes up the public key. The blue balls.

Select two prime no's. Suppose P = 53 and Q = 59. Now First part of the Public key : n = P*Q = 3127. We also need a small exponent say e : But e Must be an integer. Not be a factor of Φ(n). 1 < e < Φ(n) [Φ(n) is discussed below], Let us now consider it to be equal to 3. Our Public Key is made of n and e

Generating Private Key

The pair of numbers (n, d) makes up the private key. The orange balls.

We need to calculate Φ(n) : Such that Φ(n) = (P-1)(Q-1)
so, Φ(n) = 3016 Now calculate Private Key, d : d = (k*Φ(n) + 1) / e for some integer k For k = 2, value of d is 2011.

Implementation of the RSA algorithm

Encrypting and decrypting small numeral values:

Pseudo code

RSA Algorithm in C++:

Output:

Encrypting and decrypting plain text messages containing alphabets and numbers using their ASCII value

C++:

Output:

Implementation of RSA Cryptosystem using Primitive Roots in C++

Step 1: Generating Keys:

To start, we need to generate two large prime numbers, p and q. These primes should be of roughly equal length and their product should be much larger than the message we want to encrypt.

We can generate the primes using any primality testing algorithm, such as the Miller-Rabin test. Once we have the two primes, we can compute their product $n = p*q$, which will be the modulus for our RSA system.

Next, we need to choose an integer e such that 1 < e < phi(n) and $gcd(e, phi(n)) = 1$, where phi$(n) = (p-1)*(q-1)$ is Euler’s totient function. This value of e will be the public key exponent.

To compute the private key exponent d, we need to find an integer d such that $d*e = 1 (mod phi(n))$. This can be done using the extended Euclidean algorithm.

Our public key is (n, e) and our private key is (n, d).

Step 2: Encryption:

To encrypt a message m, we need to convert it to an integer between 0 and n-1. This can be done using a reversible encoding scheme, such as ASCII or UTF-8.

Once we have the integer representation of the message, we compute the ciphertext c as $c = m^e (mod n)$. This can be done efficiently using modular exponentiation algorithms, such as binary exponentiation.

Step 3: Decryption:

To decrypt the ciphertext c, we compute the plaintext m as $m = c^d (mod n)$. Again, we can use modular exponentiation algorithms to do this efficiently.

Step 4: Example:

Let’s walk through an example using small values to illustrate how the RSA cryptosystem works.

Suppose we choose p = 11 and q = 13, giving us n = 143 and phi$(n) = 120$. We can choose e = 7, since gcd(7, 120) = 1. Using the extended Euclidean algorithm, we can compute d = 103, since $7*103 = 1 (mod 120)$.

Our public key is (143, 7) and our private key is (143, 103).

Suppose we want to encrypt the message “HELLO”. We can convert this to the integer $726564766$, using ASCII encoding. Using the public key, we compute the ciphertext as $c = 726564766^7 (mod 143) = 32$.

To decrypt the ciphertext, we use the private key to compute $m = 32^103 (mod 143) = 726564766$, which is the original message.

See Also

• Difference between Symmetric and Asymmetric Key Encryption